Минимизация логических функций
•На основе таблицы истинности довольно просто получить СДНФ или СКНФ, затем по ним можно реализовать непосредственно цифровое устройство из базовых ЛЭ. Однако, полученная таким образом схема, как правило, не оптимальна с точки зрения её практической реализации: она громоздка, содержит много элементов (часто излишних).
•Поэтому одной из основных задач синтеза цифрового устройства является минимизация логических функций, т.е. отыскание наиболее простых логических выражений, определяющих эти функции. Все методы минимизации основываются на тождественных преобразованиях логических выражений. Основная задача минимизации состоит в получении минимальной формы булевой функции, т.е. такой формы, которой соответствует логическая схема с минимальным числом элементов.
•После минимизации, понимаемой в таком смысле, возможно выполнение других преобразований полученной функции с целью сокращения числа типов логических элементов, приведение функции к тому виду, при котором ее удобно реализовать с помощью заданных конкретных элементов, например, элементов ИЛИ-НЕ и др.
•Однако применяемые в настоящее время систематические (алгоритмизируемые) методы упрощения формул не решают задачу в таком объеме. Наиболее детально разработаны методы решения канонической задачи минимизации булевых функций, которая заключается в отыскании ДНФ (КНФ) функции, содержащей минимальное число вхождений аргументов (переменных), такие формы функций принято называть минимальными ДНФ (КНФ) – МДНФ, МКНФ.
•К систематическим методам минимизации, предполагающим применение формализованного порядка упрощения формул, относятся методы Квайна, Квайна – Мак-Класки, Блейка, Вейча – Карно и др. Эти методы описываются строгими алгоритмами и поддаются программированию, их применение дает возможность использовать ЭВМ, что является неизбежным при минимизации логических функций с большим числом аргументов.
•Для числа переменных n ≤ 6 наиболее приемлемыми являются методы Квайна и диаграмм (карт) Вейча – Карно.
Минимизация логических функций методом Квайна
•Метод Квайна предусматривает выполнение двух основных этапов: o получение сокращенной ДНФ из СДНФ;
o построение, исходя из сокращенной, тупиковых ДНФ, и выбор из их числа МДНФ.
•На первом этапе к СДНФ применяют операции склеивания
и поглощения
Результаты склеивания теперь играют роль дополнительных членов. Необходимо найти все возможные пары членов (каждый член с каждым). Если в СДНФ выполнить все операции склеивания, а затем все операции поглощения, то в результате будет получена сокращенная ДНФ.
С помощью операции поглощения на первом этапе минимизации исключаются только те члены ДНФ, к которым применены все возможные для них склеивания.
Склеивание происходит между смежными минтерами (конституентами единицы). Смежными называются минтермы, отличающиеся формой вхождения в них лишь одного аргумента (в один минтерм аргумент входит в прямой форме, а другой – в инверсной).
Два смежных минтерма склеиваются, что приводит к замене их конъюнкцией с числом аргументов (n-1) на единицу меньшим, чем в исходных минтермах.
Импликантами или контермами называются конъюнкции, получаемые в результате склеивания двух смежных минтермов. Пусть из таблицы истинности получена СДНФ функции Y, включающая пять минтермов:
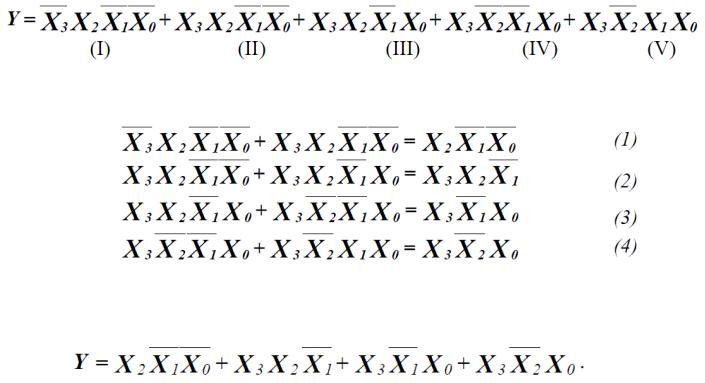
Минимизация логических функций методом Квайна
Склеивая попарно минтермы (I) и (II), (II) и (III), (III) и (IV), (IV) и (V) функции Y получим импликанты (1) – (4):
Полученные импликанты более не склеиваются и называются простыми (или первичными). Они покрывают склеиваемые минтермы и, следовательно, функция Y принимает следующий вид:
ДНФ функции, состоящая из простых импликант, называется сокращенной ДНФ.
На втором этапе используют таблицу простых импликант, представляющую собой прямоугольную таблицу, называемую импликативной. Столбцы такой таблицы являются минтермами минимизируемой функции, строки
– ее различными простыми импликантами. Если некоторый минтерм покрывает какая – либо из простых импликант, то на пересечении соответствующих столбца и строки ставится метка (например, +).
Получение тупиковых ДНФ с помощью таблицы простых импликант связано с построением на ее основе так называемой сокращенной таблицы простых импликант.
Минимизация логических функций методом Квайна
Такая таблица получается при вычеркивании из таблицы простых импликант:
1)тех столбцов, которые содержат только по одной метке;
2)тех строк, импликанты которых содержат метки в вычеркнутых столбцах;
3)одного из тех двух столбцов, у которых имеются метки в одинаковых строках;
4)тех строк, которые в результате (в соответствии с п. 1-3) не содержат ни одной метки.
Построению тупиковой ДНФ при этом соответствует выбор такой совокупности простых импликант, которая включает все те импликанты, которые принадлежат строчкам, вычеркнутым в соответствии с п. 2 (так называемое ядро булевой функции), и, кроме того, некоторую систему импликант из сокращенной таблицы, метки которых, по крайней мере, один раз накрывают все ее столбцы. В отличие от ядра такая система в общем случае может содержать различные наборы простых импликант. Выбор набора импликант с минимальным суммарным числом переменных при нескольких возможных вариантах соответствует построению минимальной ДНФ заданной функции.
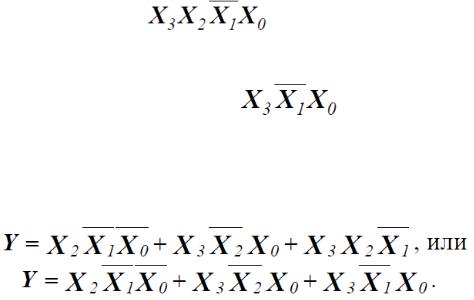
Минимизация логических функций методом Квайна
В таблице в соответствии с п.1 правил вычеркнем первый и последний столбцы, и первую и последнюю строки (п.2 правил). Данные импликанты составляют ядро минимальной тупиковой формы сокращенной ДНФ функции. Затем, выполняя пункт 3, можно вычеркнуть один столбец, соответствующий минтерму
Теперь для покрытия этого оставшегося минтерма нужно выбрать одну из простых импликант
или
Другая из этих импликант, покрывающая уже покрытые минтермы, будет избыточной и не влияет на задание функции. Таким образом, минимальная тупиковая форма сокращенной ДНФ функции Y может быть записана в двух вариантах:
•Выбор оптимальной минимальной тупиковой формы для реализации функции в данном случае будет определяться удобством реализации.
•Может существовать несколько тупиковых ДНФ функций. Искомая оптимальная МДНФ совпадает с той из тупиковых ДНФ, которая содержит минимальное число вхождений аргументов.
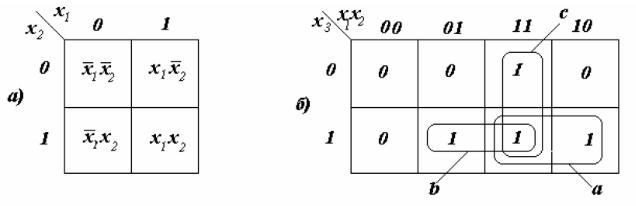
Минимизация логических функций методом карт Карно
•Карта Карно или усовершенствованная диаграмма Вейча представляет собой прямоугольную таблицу специального вида, используемую для задания булевых функций и применяемую с целью упрощения списка тупиковых и минимальных ДНФ функций. Карта Карно может использоваться и как способ задания логических функций, она взаимно однозначно соответствует таблице истинности.
•Удобство и наглядность такого представления логической функции обусловлено тем, что логические термы, к которым могут быть применены операции попарного неполного склеивания и элементарного поглощения группируются в карте Карно в виде массивов соседних ячеек по вертикалям и горизонталям логических единиц или нулей, что человеку сразу наглядно видно.
•Графически карта Карно для функции n аргументов изображается в виде прямоугольника или квадрата из ячеек, число которых равно 2n, причем любые две соседние ячейки по вертикали или горизонтали описывают термы, различающиеся только по одной переменной — с логическим отрицанием и без логического отрицания. Также соседним являются первая и последняя строки, крайний левый и крайний правый столбцы таблицы.
•Возможно построение самых различных карт для одной и той же функции. Любая из таких таблиц одинаково удобна для минимизации функции, но обычно переменные по строкам и столбцам в карте Карно упорядочивают по определенным правилам для наглядности процедуры минимизации логической функции.
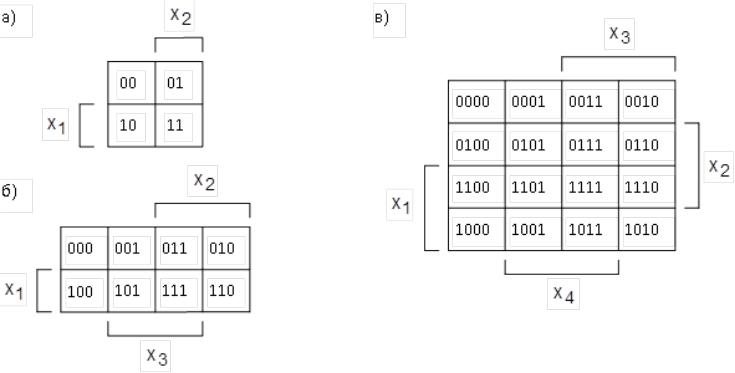
Минимизация логических функций методом карт Карно
Клетки кодируются всеми возможными наборами аргументов логической функции. Количество клеток равно количеству всех возможных наборов аргументов. Клетки можно кодировать не только двоичным представлением комбинации аргументов функции, но ее десятичным эквивалентом.
Как и в обычной таблице истинности, в клетках карты Карно проставляются значения функции 0 или 1, соответствующие наборам аргументов клетки.
Представление описания логической функции в виде карты Карно облегчает поиск таких дизъюнктивных членов в СДНФ (или конъюнктивных членов в СКНФ), над которыми можно производить операции склеивания. Операция склеивания эквивалентна объединению соответствующих клеток в одну область, для которой результирующий дизъюнктивный член в СДНФ (или конъюнктивный член в СКНФ) будет содержать конъюнкции (дизъюнкции) только тех переменных, которые для данной выделенной области не изменяют своих значений на инверсные.
Минимизация логических функций методом карт Карно
Пример 1.
Функция имеет СДНФ
Операции склеивания можно провести над первым и вторым дизъюнктивными членами, а также над третьим и четвертым. Первая операция склеивания соответствует объединению верхних двух клеток карты Карно в область 1, а вторая операция склеивания - объединению нижних двух клеток в область 2.
Минимизация логических функций методом карт Карно
В результате первой операции два первых дизъюнктивных члена заменяются одним эквивалентным, не зависящим от переменной x4, в результате второй операции третий и четвертый дизъюнктивные члены
заменяются эквивалентным, который также не зависит от переменной x4. При этом логическая функция приводится к виду
В этом выражении опять имеются два дизъюнктивных члена, отличающихся только прямым и инверсным значениями переменной x1. Следовательно, над ними опять можно провести операцию склеивания, что даст
окончательное выражение для МДНФ в виде
Эта последняя операция склеивания на карте Карно отображается объединением двух выделенных областей 1 и 2 в единую область 3 путем сворачивания карты в цилиндр и совмещения верхней и нижней строк. Точно так же можно сворачивать карту в цилиндр для совмещения левого и правого крайних столбцов. Возможно и объединение в одну область четырех угловых клеток карты Карно.
Правила минимизации:
а) клетки карты Карно, содержащие значения логической функции, равные единице, объединяются в замкнутые области прямоугольной формы, при этом каждая выделенная область может содержать 2, 4, 8, или 16 клеток. Области могут пересекаться и одни и те же клетки могут входить в разные области;
Минимизация логических функций методом карт Карно
б) следует стремиться провести объединение клеток таким образом, чтобы количество выделенных областей было минимальным, а в каждую область входило бы максимально возможное число клеток. Это позволяет получить наиболее простой вид МДНФ;
в) в результирующей записи МДНФ число дизъюнктивных членов будет равно числу выделенных областей. Каждый дизъюнктивный член представляется конъюнкцией только тех переменных, которые во всей соответствующей этому члену выделенной области не изменяют своего значения с прямого на инверсное, то есть сохраняют свои значения неизменными. Клетки, которые не могут быть объединены ни с какими другими, также представляются отдельными дизъюнктивными членами, содержащими конъюнкции всех переменных логической функции;
г) для получения МКНФ замкнутыми областями охватываются клетки с нулевыми значениями минимизируемой функции. МКНФ будет содержать число конъюнктивных членов, равное числу выделенных областей. Каждый конъюнктивный член будет содержать дизъюнкции инверсий тех переменных, которые для соответствующей этому члену области не изменяют своих значений.
При минимизации с помощью карт Карно неполностью определенной логической функции, то есть функции, определенной не на всех возможных наборах аргументов, в клетках, где функция не определена, ставятся прочерки. В этих клетках функция доопределяется произвольным образом (то есть ей можно приписать значения либо логического нуля, либо логической единицы). Доопределение производится таким образом, чтобы облегчить выделение областей максимального размера.