
СПИНТех - Прикладная информатика / ЧМ_ЛР-6_Толстов_П-31
.docxМинистерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное
учреждение высшего образования
Национальный исследовательский университет “МИЭТ”
Институт Системной и программной инженерии и информационных технологий
Дисциплина: Численные методы
Лабораторная работа №6
«Решение задачи Коши для обыкновенных дифференциальных уравнений»
Вариант 21
Выполнил:
Студент П-31
Толстов Д.В.
Преподаватель:
Лавров И.В.
Москва 2022
Теория:
Конкретная прикладная задача может приводить к дифференциальному уравнению любого порядка, при этом обыкновенное дифференциальное уравнение (ОДУ) p -го порядка
можно привести к эквивалентной системе p дифференциальных уравнений первого порядка путем введения новых переменных
Где k=0, 1, … , p-2. Для решения задачи Коши введем по переменной t равномерную сетку с шагом τ > 0, т.е. рассмотрим множество точек ωt = {tn = τn , n = 0,1,...}. Будем обозначать через u(t) точное решение, а через yn = u(tn) - сеточное, определенное только в точках сетки ωτ. Принимая, что t = tj и t + τ = tj+1 , получаем явную формулу Эйлера для решения задачи Коши:
Неявная формула Эйлера
В случае, если для нахождения решения используется только значение функции на предыдущем шаге, методы называют одношаговыми, если же необходимо знание значений функции в более чем одном предыдущем шаге, методы относят к многошаговым. Одношаговые методы Рунге - Кутты. Пусть u(t) - решение дифференциального уравнения u′(t) = f (t,u). Запишем равенство, вытекающее из формулы Ньютона - Лейбница, в следующем виде:
Заменим интеграл квадратурной суммой:
Перепишем равенство (5):
Подставим и получим:
, где
Полученная рекуррентная система задает явный одношаговый метод вычисления решения, использующий m вспомогательных значений правой части на элементарном отрезке [tn , tn+1], поэтому его называют m - этапным методом Рунге - Кутты. Кроме этого, если |fu (t,u(t))| ≤ L ( L = const ≤ ∞), то m - этапный метод Рунге - Кутты устойчив на конечном отрезке. Если, кроме этого, он имеет p -й порядок аппроксимации, то метод сходится с p -м порядком точности. |
Задание:
Выбрать задание согласно номеру варианта:
![]()
Решить ОДУ, написав m-файл. Использовать явный метод Эйлера и метод Рунге - Кутты 4-го порядка. Решить ОДУ с использованием оператора ode45. Построить графики, сравнить результаты.
В отдельном файле (func1.m) записали функцию:
function u_res = func1(t,u) u_res = exp(-1*t)*(3+u^2); end |
Основной файл:
#-----метод Эйлера a = 0; b = 1; n = 50; h = (b-a)/n; t = a:h:b; u0 = 0; u = zeros(1,n+1); u(1) = u0; for i1 = 1:n u(i1+1) = u(i1) + h * func1(t(i1),u(i1)); end
u_e = u; plot(t,u_e)
#-----метод Рунге-Кутты
for i1 = 1:n k1 = func1(t(i1),u(i1)); k2 = func1(t(i1)+h/2,u(i1)+h*k1/2); k3 = func1(t(i1)+h/2,u(i1)+h*k2/2); k4 = func1(t(i1)+h,u(i1)+h*k3); u(i1+1) = u(i1)+h/6*(k1+2*k2+2*k3+k4); end u_r=u; plot(t,u_e,'g',t,u_r,'b') #-----стандартные методы [T,u_m] = ode45('func1',t,u0); figure(2) plot(T, u_m); |
Явный метод Эйлера и метод Рунге-Кутты 4-го порядка:
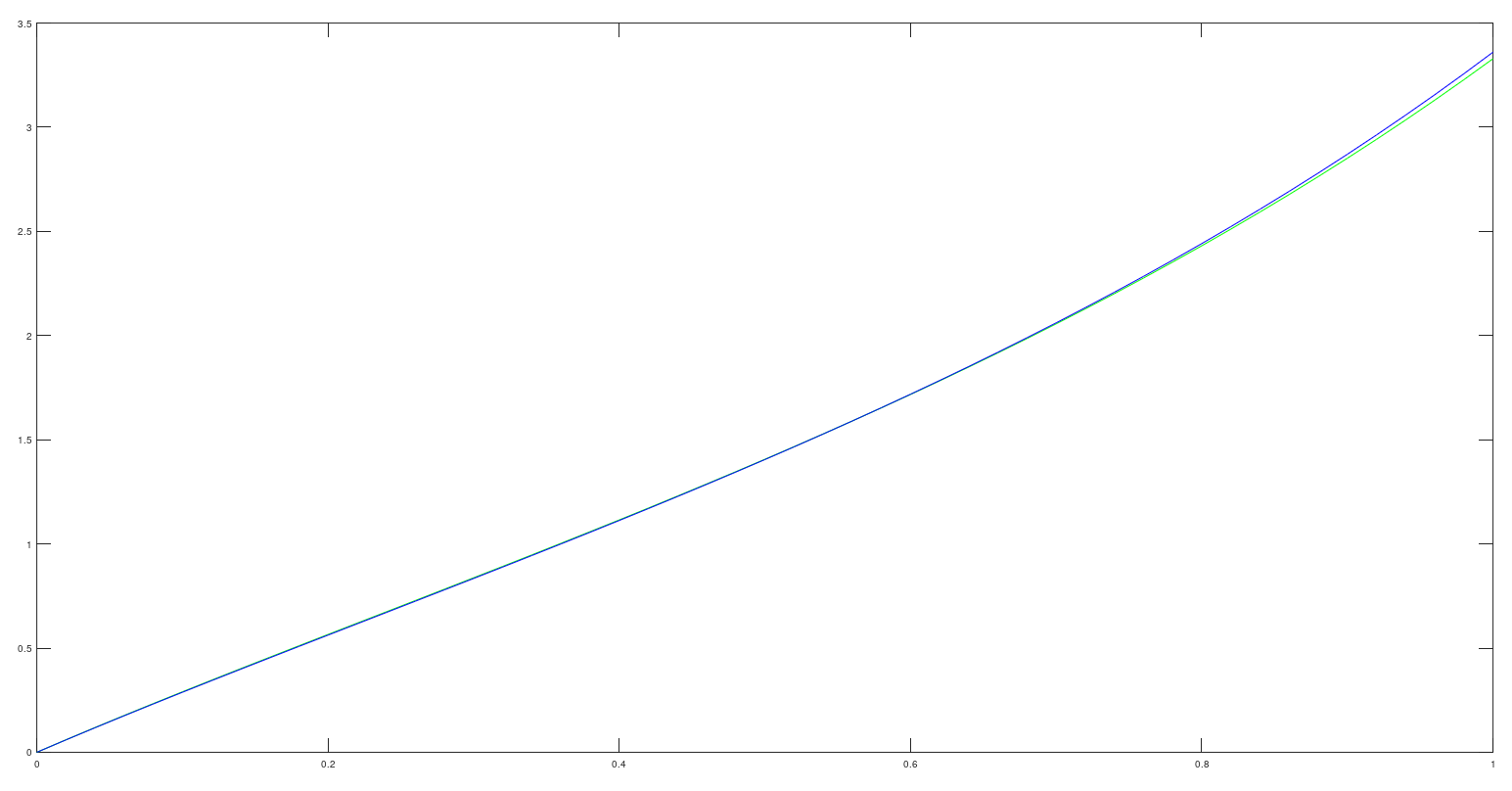
Использование ode45:

Сравнение результатов:

Красный цвет (ode45) полностью совпадает с синим (метод Рунге-Кутты) в отличие от зеленой кривой (явный метод Эйлера), из чего следует вывод, что вывод Рунге-Кутты работает точнее явного метода Эйлера.
Вывод: в данной лабораторной работе мы изучили метод численного решения задачи Коши для обыкновенных дифференциальных уравнений; приобрели навыков программирования методов решения задачи Коши для обыкновенных дифференциальных уравнений; приобрели навыков использования стандартных средств системы Matlab для решения задачи Коши для обыкновенных дифференциальных уравнений.






