Элементарные функции и их графики

в соответствие число x n (рис. 2в). Эта функция называется дробной частью числа х и обозначается y {x}.

4. Функция Хевисайда – специальная математическая

функция, значение которой		равно
нулю для отрицательных аргумен-			у
			1
тов и единице для неотрицательных
	1,	x 0,		х
аргументов:	y (x) 0,	x 0	–1	Рис. 2г

(рис. 2г). Функция широко используется в теории управления и обработке сигналов для представления сигналов, включающихся в определенный момент и остающихся включенными постоянно.

5. Функция		модуля или	абсолютного значения
y | x | x,	x 0,	(рис. 2д).	у
x,	x 0

	Функции, приведенные в приме-
	рах 1–5, несмотря на свою простоту,	х
		Рис. 2д
	элементарными не являются.

§ 3. Сложная функция

Познакомимся с понятием суперпозиции функций, которое состоит в том, что в качестве аргумента одной функ-

ции	используется другая функция,		то	есть из	функций
z f (x) и y g(z) получают функцию y F (x) .
	Определение 3.1. Пусть задано три множества X, Y,
Z и	две функции	f : X Z	и	g : Z Y ,	причем
E( f ) D(g) . Функция		F : X Y называется суперпозици-

ей (композицией) функций f (x) и g(z) или сложной

21

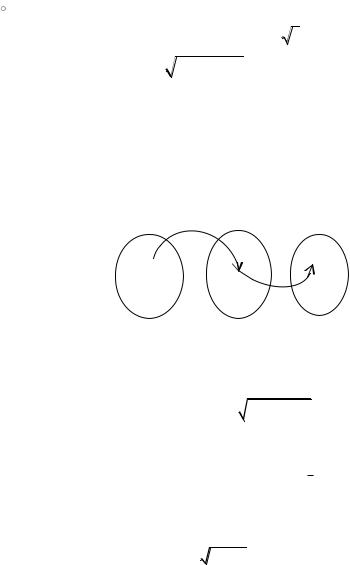
функцией,		если	выполняется			соотношение
F(x) (g	f )(x) g( f (x)) .
Например:		z f (x) x3 9x 7 , y g(z) 3						.	Тогда
							z
сложная	функция y g( f (x)) 3 x3 9x 7 .					Чтобы			найти

значение сложной функции, подставляют сначала заданное значение x0 во внутреннюю функцию и находят ее значение z0 f ( x0 ) , а затем уже вычисляют соответствующее значе-

ние функции y0 g(z0 ) .

При выполнении суперпозиции функций считают, что

множество	значений	Х				Z	Y
внутренней	функции
				f
f (x) содержится в об-		х				g		у
					z
ласти	определения

внешней функции g(z) .
Сложную функ-	Рис. 3

цию можно составить из большего числа более простых функций.

Пример 1. Сложную функцию f (x) log2 cos x пред-

ставьте в виде цепочки элементарных функций.

Решение. Будем последовательно выполнять операции, которые заданы в формуле: z cos x , t log2 z , y t . Следовательно, заданная в условии задачи функция является су-

перпозицией трех основных элементарных функций.				◊
Пример 2. Даны функции y		3z 8, z t7 , t sin u,
u 2x . Запишите сложную функцию	y f (x) .

22

Решение. Подставляя последовательно функции одну в

другую, получим сложную функцию y 3sin7 2x 8 . ◊

§ 4. Обратная функция

Пусть функция y f (x) , определенная на множестве Х, такова, что любым двум различным значениям аргумента х ставит в соответствие различные значения у, то есть, если x1 x2 , то y1 f (x1) f (x2 ) y2 . Эта функция устанавливает взаимнооднозначное соответствие между областью своего определения Х и областью изменения Y.

Действительно, каждой точке				x X ставится в соот-
ветствие единственное y Y . При этом каждой точке							y Y
соответствует	единственное				Y
x X , такое, что	y f (x) . Та-			Х
Таким образом, на множестве
				х			у
Y определена функция f		1	, ко-

Рис. 4а

торая называется обратной к

функции f. Область определения обратной функции – множе-

ство Y, область значений – мно-					у
жество	Х.	Графики	функции
y f (x)	и	обратной	к	ней
функции	y	f 1 (x) симметрич-
ны относительно прямой				y x			х
						Рис. 4б
(рис. 4б). Для обратных функций

верно соотношение f ( f 1(x)) f 1( f (x)) x .

23

Для нахождения обратной функции необходимо из ра-

венства

y f (x)

выразить х через у, и в полученном выра-

жении x f 1 ( y)

букву х заменить буквой у, букву у – бук-

вой х.

Пример

3.

Имеют ли

функции f (x) 0,5(7x 3)

и

g(x) x4

1 обратные? Если да, то найдите их.

Решение. Выразим х из формулы

y 0,5(7x 3) . Полу-

чим

x

2 y 3

. Обозначив аргумент через х,

а функцию че-

7

рез у, получим y

2x 3

, то есть функция

f 1(x)

2x 3

7

7

является обратной к функции

f (x) 0,5(7x 3) .

Функция

g(x) x4 1 не имеет обратной, так как она

не

является

взаимнооднозначной.

Действительно,

g( 1) g(1) 2 .

◊

Пример

4.

Являются

ли

функции

f ( x) x2

и

g( x)

x взаимообратными?

Решение. Нет, так как

g( f (x))

x2 | x | x .

Однако,

если данные функции рассматривать только при

x 0 ,

то

есть

считать

D( f ) [0; ) ,

то

эти

функции становятся

взаимообратными.

◊

§5. Свойства функций

Вданном параграфе будут приведены определения основных свойств числовых функций числового аргумента, то

24

есть будут рассматриваться функции f (x), для которых

D( f ) R и E( f ) R .

Определение 5.1. Функция y f (x) называется монотонно возрастающей на множестве X D( f ) , если для любой пары точек x1, x2 X из условия x1 x2 следует, что f (x1) f (x2 ) , то есть большему значению аргумента соот-

ветствует большее значение функции.
Определение 5.2. Функция	y f (x)	называется моно-
тонно убывающей на множестве	X D( f ) ,		если для лю-
бой пары точек x1, x2 X из условия x1		x2	следует, что

f (x1) f (x2 ) , то есть большему значению аргумента соответствует меньшее значение функции.

Определение 5.3. Функция y f (x) называется неубывающей на множестве X D( f ) , если для любой пары точек x1, x2 X из условия x1 x2 следует, что f (x1) f (x2 ) , то есть большему значению аргумента соответствует большее или равное значение функции.

Определение 5.4. Функция y f (x) называется невозрастающей на множестве X D( f ) , если для любой пары точек x1, x2 X из условия x1 x2 следует, что f (x1) f (x2 ) , то есть большему значению аргумента соответствует меньшее или равное значение функции.

Монотонно возрастающие и монотонно убывающие функции называют монотонными.

Монотонные функции обладают следующими свойст-

вами:

25

1)сумма двух монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;

2)произведение двух положительных монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;

3)если функция y f (x) монотонно возрастающая

(монотонно убывающая), то функция y f (x) монотонно убывающая (монотонно возрастающая);

4) если положительная функция y f (x) является монотонно возрастающей (монотонно убывающей), то функция

y	1	является монотонно убывающей (монотонно воз-
	f ( x)

растающей);

5) если функция y f (x) монотонна на всей области определения, то она имеет обратную функцию;

6) если функция z g(x) монотонно возрастает (моно-

тонно убывает) на множестве X,			а функция y f (z)			моно-
тонно возрастает (монотонно убывает) на множестве						g( X ) ,
то сложная функция y f (g(x))			монотонно возрастает (мо-
нотонно убывает) на множестве X.
Пример 5.	Функцию	f (x) x2 3x 5 исследуйте на
монотонность при x [0; ) .
Решение.	Пусть	0 x1	x2 .	Тогда	разность

f (x2 ) f (x1 ) (x22 3x2 5) (x12 3x1 5) (x2 x1 )(x2 x1 3) 0 .

26

Следовательно,	f (x1) f (x2 ) и функция f (x) является воз-
растающей.	◊

Заметим, что функции y = [x], y = sgn x и y = χ(x) являются неубывающими на всей числовой прямой, а функция y = {x} возрастает на каждом промежутке [n; n + 1), где n Z . Функция y = |x| убывает при x 0 и возрастает при x 0.

Определение 5.5. Функция y f (x) называется ограниченной сверху на множестве X D( f ) , если существует такое число М, что значение функции в любой точке не превосходит этого числа, то есть для любого x X выполняется неравенство f (x) M .

Определение 5.6. Функция y f (x) называется ограниченной снизу на множестве X D( f ) , если существует такое число m, что значение функции в любой точке не меньше этого числа, то есть для любого x X выполняется неравенство f (x) m .

Ограниченная сверху и снизу на множестве Х функция называется ограниченной на этом множестве. Другими словами, если функция f (x) ограничена на множестве Х, то существуют такие числа m и М, что m f (x) M для всех x X . Условие ограниченности можно также записать в виде | f (x) | M для некоторого положительного числа М.

Пример 6. Является ли функции f (x) 9 8x x2 ограниченной?

Решение. Область определения функции найдем из условия 9 8x x2 0 , то есть D( f ) [1; 9] . Преобразуем

27

подкоренное			выражение 9 8x x2		9 (16 8x x2 ) 16
25 (x 4)2 ,
			значит f (x)	25 (x 4)2 . Имеем			f (x) 0 ,
так как		корень арифметический.			С другой		стороны
f (x) 25		5 . Следовательно, функция ограничена и свер-
ху и снизу, причем 0 f (x) 5 .							◊
Заметим,			что функции y = sgn x, y = {x}, y = χ(x) ограни-

чены на всей области своего определения, а функция y = |x| ограничены снизу, но не ограничены сверху.

Определение 5.7. Точка x0 D( f ) называется точкой максимума функции y f (x) , если существует окрестность этой точки такая, что для всех точек x x0 из этой окрестности выполняется неравенство f ( x) f ( x0 ) .

Определение 5.8. Точка x0 D( f ) называется точкой минимума функции y f (x) , если существует окрестность этой точки такая, что для всех точек x x0 из этой окре-

стности выполняется неравенство f ( x) f ( x0 ) .

Точки максимума и минимума называют точками экс-

тремума функции.

Заметим, что функция в области своего определения может иметь несколько точек максимума или минимума.

Пример 7. Докажите, что точка x0 3 является точкой

максимума для функции f (x) 1 . 2x2 12x 19

Решение. Областью определения функции является вся числовая прямая, так как знаменатель 2x2 12x 19 всегда

28

отличен

от

нуля

( D 8).

Преобразуем

знаменатель

2x2 12x 19 2(x 3)2 1 . Значит,

f (x) 1

при

x = 3 и

f (x) 1

при x 3. Что и означает наличие максимума в точ-

ке x0 3 .

◊

Заметим,

что точка x0 = 0 является точкой минимума

для функций y = |x| и y x2 .

Определение

5.9.

Будем

говорить,

что

в

точке

x0 X D( f ) функция

y f (x)

принимает наибольшее на

множестве Х значение,

если для всех точек

x X

справед-

ливо неравенство

f ( x)

f ( x0 ) .

Определение

5.10.

Будем

говорить,

что

в

точке

x0 X D( f ) функция

y f (x) принимает наименьшее на

множестве Х значение,

если для всех точек

x X

справед-

ливо неравенство

f ( x)

f ( x0 ) .

Если множество Х представляет собой отрезок [a; b], то наибольшее или наименьшее значения функция принимает, либо в точке экстремума, либо на конце отрезка.

a	b	a	b	a	b
Говорят, что множество Х симметрично относитель-
но начала координат, если для любой точки					x X проти-
воположная точка x X .

29

Определение 5.11. Функция y f (x) называется четной, если ее область определения симметрична относительно начала координат, и f (x) f (x) для любого x D( f ) .

Определение 5.12. Функция y f (x) называется нечетной, если ее область определения симметрична относительно начала координат, и f (x) f (x) для любого x D( f ) .

График четной функции имеет ось симметрии. Если точка М0(х0; у0) принадлежит графику четной функции, т. е. x0 D( f ) и y0 f (x0 ) , то x0 D( f ) , f ( x0 ) f (x0 ) y0 и

точка М1(–х0; у0) принадлежит графику этой функции. Следовательно, он симметричен относительно оси ординат. Верно и обратное утверждение: если график функции f (x) симметричен относительно оси ординат, то функция f (x) четная.

График нечетной функции имеет центр симметрии. Если точка М0(х0; у0) принадлежит графику нечетной функции,

т. е. x0 D( f )	и y0 f (x0 ) , то	x0 D( f ) ,	f ( x0 )
f (x0 ) y0	и точка М1(–х0; –у0)	принадлежит	графику

этой функции. Следовательно, он симметричен относительно начала координат. Верно и обратное утверждение: если график функции f (x) симметричен относительно начала координат, то функция f (x) нечетная.

Функции, которые не являются ни четными, ни нечет-

ными, называют функциями общего вида.

Четные и нечетные функции обладают следующими свойствами:

30