Нечеткая логика и нейронные cети

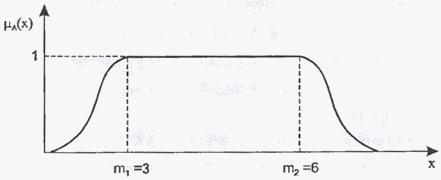
71

Рассмотрим неточное утверждение «стоимость велосипеда в этом магазине составляет от 3 до 6 тысяч рублей». Адекватной формализацией этого утверждения может считаться нечеткий интервал 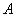вида

A=(3,6,α, β)LR

(3.139)

На рис. 1.4.6 представлен примерный график функции принадлежности нечеткого интервала.

Рис. 1.4.6. Нечеткий интервал «от 3 до 6 тысяч рублей».

1.5. Основные операции на нечеткими множествами

Нечеткая логика создавалась на основе классической четкой логики, имеющей недостатки вследствие своей двузначности. Введение понятия нечеткого множества повышает точность моделирования, но различные обобщения

(расширения) приводят к неоднозначности определений, имеющих аналогии и в классической теории множеств.

1. Любое определение операции справедливо, если вместо нечетких множеств используются классические множества. Термин функции принадлежности заменяется на характеристические функции. Хотя в принципе это одно и то же,

вследствие принципа обобщения

2. Сравнение нечетких множеств и выполнение над ним различных операций возможно при определении их на одном и том же универсуме.

72

3.Одна и та же функция принадлежности может описывать различные качественные понятия, поэтому свойство в форме нечеткого множества выражает различные субъективные функции и различные нечеткие множества.

4.Операции определяются через действия над их функциями принадлежности.

Операция пересечения.

Операцию пересечения нечетких множеств представляется как расширение соответствующей операции над обычными множествами. Поэтому пересечение обычных множеств является частным случаем пересечения нечетких множеств.

В классической логике пересечение множеств А и В определяется без использования функций принадлежности по формуле

Основные свойства операции пересечения нечетких множеств А и В, заданных на универсальном множестве X , также как четких множеств, определяются следующими соотношениями, графическое представление на рис. 1.5.1.

Рис. 1.5.1. Графическое представление операции пересечения нечетких множеств.

Коммутативность:

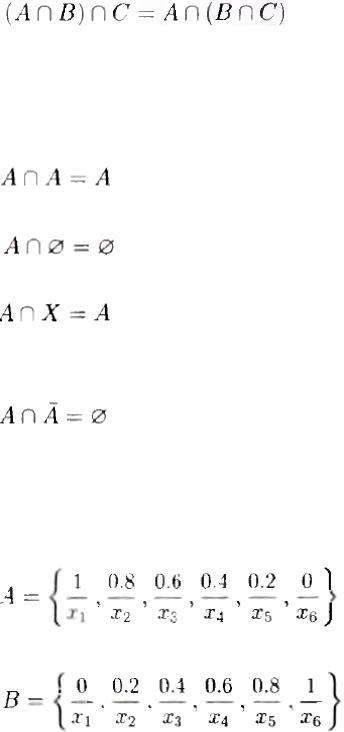
73

Свойство означает, что порядок следования множеств-операндов не влияет на конечный результат.

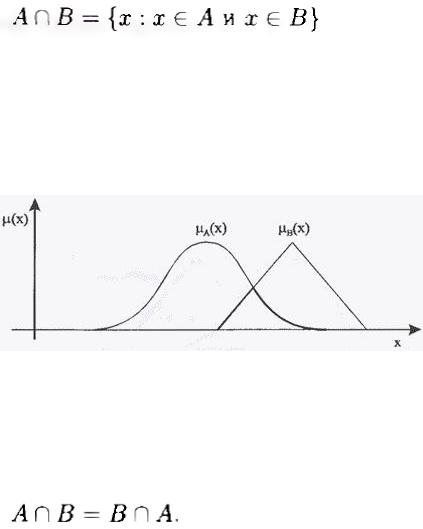
Ассоциативность:

Свойство определяет возможность пошагового вычисления логического произведения нескольких множеств путем нахождения произведений их пар.

Порядок, в котором формируются пары, не влияет на конечный результат.

Идемпотентность:

Поглощение (пересечение с пустым множеством 0):

Тождественность (пересечение с универсальным множеством):

где X — универсальное множество.

Закон логического противоречия:

Для нечетких множеств последняя операция может быть задана различными способами и потому имеет неоднозначный смысл.

Имеются два нечетких множества А и В, где A —множество дешевых автомобилей, B — множество комфортабельных автомобилей

B — множество комфортабельных автомобилей:

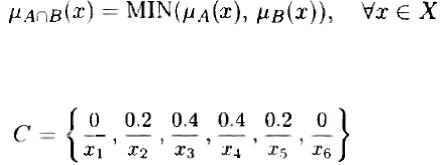
74

Нужно определить множество С автомобилей, являющихся одновременно дешевыми и комфортабельными. Поскольку А = В, то, в случае четких множеств, получили бы пустое множество.

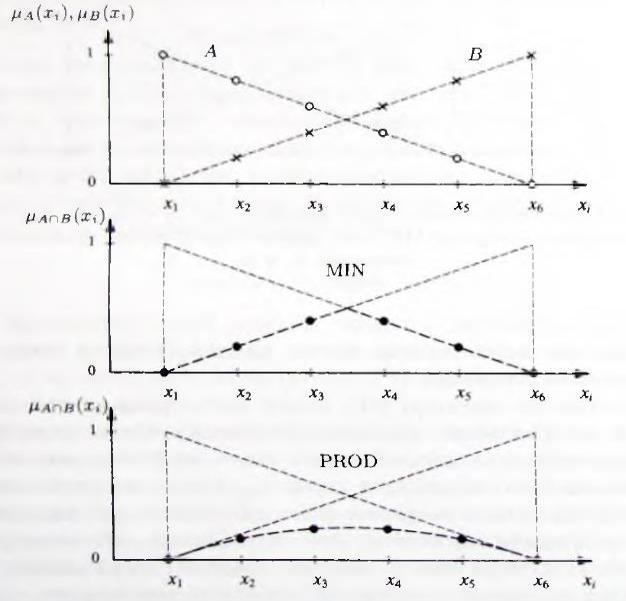
Автомобиль п 4 может быть отнесен к дешевым со степенью µ=0.4 и к комфортабельным — со степенью µ=0.6. Для определения автомобиля дешевым и комфортабельным, Л. Заде предложил вычислять значения функции принадлежности произведения множеств с использованием оператора MIN :

Применяя эту формулу для нахождения множества 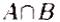дешевых и,

одновременно с этим, комфортабельных автомобилей, получаем выражение:

.

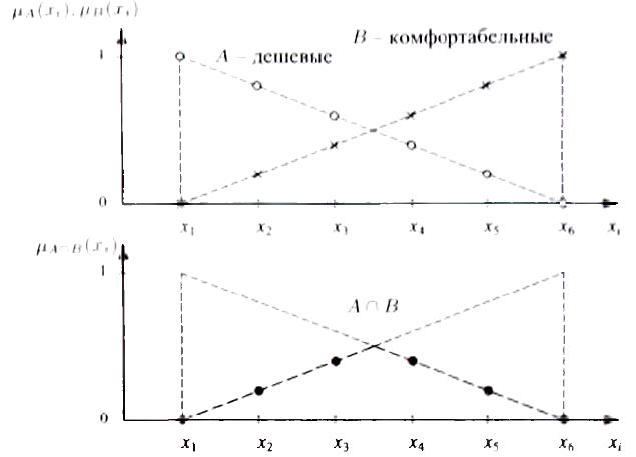
75

Рис. 1.5.2. Произведение А * В нечетких множеств дешевых (A) и

комфортабельных (B) автомобилей, полученное с использованием оператора

M1N

Достоинства операции MIN:

1.Простота и скорость вычислений.

2.Возможность «сглаживания» действия оператора MIN, при повышении объема вычислений, с понижением точности.

Недостатки операции MIN:

1.Точность модели ниже, чем при использовании других операторов.

2.Менее гладкая поверхность, чем для других операторов (оператор жесткий).

3.Нечувствительность и резкое изменение значений выходной величины модели и нечеткого регулятора, содержащих операторы MIN.

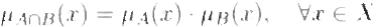
	76
Существуют	другие операторы снижающие жесткость и повышающие
точность и гладкость полученной функции.
- мягкий оператор MIN с функцией дельта.
- мягкий оператор MIN с функцией soft
- оператор PROD
Реализация	пересечения нечетких множеств операторов как MIN, так и PROD,

указывает на неоднозначность способа выполнения данной операции, поэтому оператор min (пересечение) часто выбирается интуитивно, исходя из опыта, на основе каких-либо гипотез или же методом проб.

Вычисление функции принадлежности произведения нечетких множеств с использованием оператора PROD осуществляется в соответствии с формулой

Преимущество оператора PROD в том, что значение µA∩B(x) имеет количественную зависимость от фактических значений обеих функций принадлежности µA(x) и µB(x) (за исключением случая равенства одной из функций нулю). Потеря информации здесь не так существенна, как для оператора MIN, когда значение зависит лишь от меньшего (в пределах заданной области изменения х значениq компонентов µA(x) и µB(x). Сравнение результатов вычисления логического произведения с использованием операторов MIN и PROD представлено на рис. 1.5.3.

Нечеткое расширение пересечения или t- норма
В качестве операторов пересечения А∩В используются	t -нормы,

определяющие различные формы реализации операции пересечения. Такие t-

нормы представляет собой функцию Т, моделирующую операцию пересечения двух нечетких множеств А и В, удовлетворяющую перечисленным ниже свойствам, которые выполняются для всех х € X.

77

Рис. 1.5.3. Функции принадлежности логического произведения нечетких множеств А ∩ В, полученные с использованием операторов MIN и PROD

Свойство коммутативности указывает на то, что для данной операции порядок следования множеств не является существенным. Свойство

ассоциативности	говорит о том, что операцию пересечения выполняется для
более, чем двух	множеств. Основные операции над нечеткими множествами,
необходимо выполнять последовательно, но порядок образования		пар

78

множеств не влияет на конечный результат. Свойство монотонности означает,

что при возрастании значений аргументов результат операции не убывает.

X1*X2=	1
		1*1=
	1*X2= X2
	0*0=	0*1=
		1
1*0=
1
Рис. 1.5.4. Геометрическая интерпретация t-норм
Пространства отображения:
Свойство обнуления:

,

Случай, когда пара содержит один элемент с ii(x) = 1:

Свойство коммутативности:

Свойство ассоциативности:

Условие монотонности:

79

Выделяют параметризованные и непараметризованные t-нормы. Результат действия непараметризованных t-норм является постоянным, тогда как для параметризованных t-норм он будет изменяться как количественно, так и качественно, при изменении любого параметра, являющегося степенью свободы оператора.

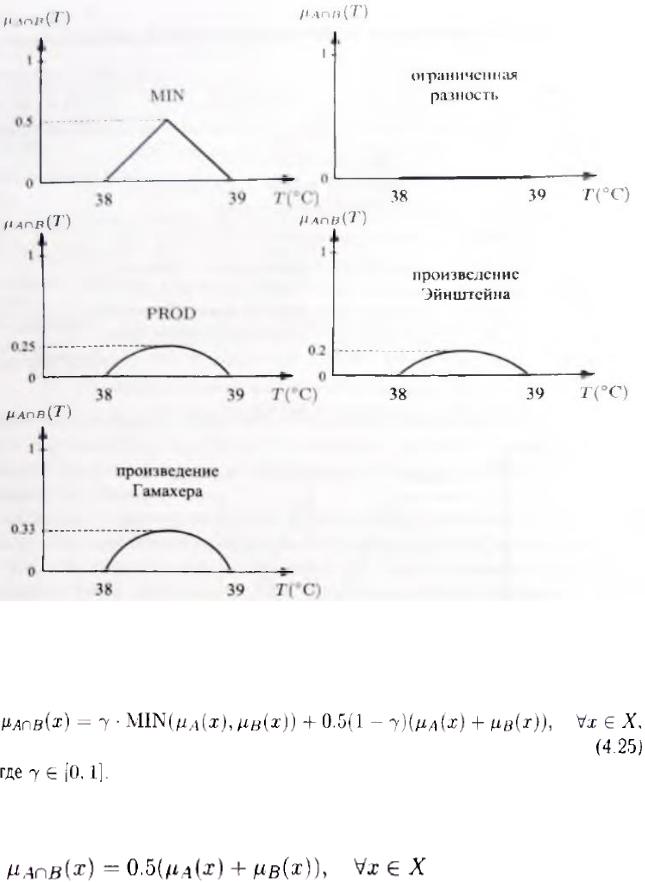
В соответствии с четкой логикой, температура не может быть одновременно средней и высокой, в то время как нечеткая логика позволяет существование такого множества. Функция принадлежности этого множества не является строго определенной и зависит от используемого оператора t-нормы.

Оператор MIN приводит к самым высоким значениям функции принадлежности, поэтому другие операторы t-норм называют sub-MIN-

операторами или sub-MIN-нормами. Значения функции принадлежности произведения множеств µA∩B(x). получаемые с помощью sub-MIN-операторов

(t-норм), будут меньше, чем при использовании оператора MIN, что означает,

что sub-MIN-операторы являются более строгими, требующими более высокой степени выполнения условий А и В, входящих в нечеткое произведение.

Поэтому об операторе MIN говорят, как о наиболее качественном среди t-норм.

Согласно степени качества, t-нормы могут быть упорядочены следующим образом: минимум > произведение Гамахера > алгебраическое произведение

> произведение Эйнштейна > ограниченная разность > усиленное произведение.

Для определения операции пересечения также используются операторы, не являющиеся t-нормами (т. е. не обладающие свойствами t-норм).

80

Рис. 1.4.5. Графические изображения операторов t - норм

Параметризованный оператор пересечения на основе среднего (Driankov 1993),

При ץ = 1 данный оператор сводится к оператору MIN. При ץ = 0 получается оператор среднего арифметического: