Дискретная математика.-1

41

состоящий только из изолированных вершин (в котором k(G) = (G) и q(G)

= 0), называется вполне несвязным.

5.2. СКЕЛЕТ ГРАФА

Скелет G^ графа G получается путём отбрасывания в графе G всех петель и заменой кратных рёбер одним эквивалентным, а также дезориентацией имеющихся дуг.

5.3. ПОКРЫВАЮЩИЕ МНОЖЕСТВА ВЕРШИН И РЁБЕР ГРАФА G

Говорят, что в графе G вершина покрывает инцидентные ей рёбра, а

ребро покрывает инцидентные ему вершины.

Множество вершин графа G, покрывающее все рёбра, называется

вершинным покрытием. Наименьшее число вершин во всех вершинных покрытиях называется числом вершинного покрытия 0 (G) .

Множество таких рёбер, которые покрывают все вершины,

называется рёберным покрытием. Наименьшее число рёбер во всех рёберных покрытиях называется числом рёберного покрытия 1(G) .

5.4. МАКСИМАЛЬНЫЕ ПОЛНЫЕ И МАКСИМАЛЬНЫЕ ПУСТЫЕ ПОДГРАФЫ

Определения

1). Подграф L’ называется максимальным пустым подграфом графа

L=(X,U), если L’ не является собственным подграфом никакого большего максимального пустого подграфа данного графа L.

42

2). Подграф L’’ называется максимальным полным подграфом графа

L=(X,U), если L’’ не является подграфом никакого большего максимального полного подграфа графа L.

5.5. КЛИКА ГРАФА.

Подмножество Хk Х вершин графа G=(X,U) называется кликой, если

Gk=(Xk, k) полный подграф некоторого графа без петель G=(X, ),

соответствующего графу G=(X,U).

Клика Хkmax называется максимальной, если Gkmax строго не содержится ни в каком другом полном подграфе графа G.

5.6. АЛГОРИТМ НАХОЖДЕНИЯ ВСЕХ МАКСИМАЛЬНЫХ ПУСТЫХ И ВСЕХ МАКСИМАЛЬНЫХ ПОЛНЫХ ПОДГРАФОВ (МАКСИМАЛЬНЫХ КЛИК) В ГРАФЕ ОБЩЕГО ВИДА

Задача выявления всех максимальных полных	и максимальных
пустых подграфов в заданном графе L (X ,U;P)	общего вида легко

сводится к случаю обыкновенных графов. Поэтому, для практического выявления всех максимальных полных и максималь-ных пустых подграфов в произвольном графе достаточно уметь выявлять только максимальные полные и максимальные пустые подграфы обыкновенных графов.

Приведём алгоритм выявления всех максимальных пустых подграфов в заданном графе общего вида , основанный на работах Х.Магу и Дж.Уэйсмана:

Шаг1.Для графа L=(X,U;P) общего вида построить его скелет

L (X ,U ).

43

Шаг 2. Построить матрицу инциденций А графа L ( X ,U ) , элементы

которой ai,j принимают значения 0 либо 1 ( i 1, n ; j 1, m , где											n = X -
число вершин в ПL , m =
		- число рёбер в L ( X ,U ) ).
	U

a

11

A a21

.

an1

a	...	a
12		1m
a22	...	a2m
.	.	.
an2	...
		anm

Шаг 3. Дополним систему логическими переменными х1, х2, …,хi,…,хn ,

которые принимают значения 0 и 1, и подчиним её условиям:

x2

x

x 1 1

;

x x x

i

i ;

i

i

i

i , 1+1=1, т.е. 2=1, (i=1,2,…,n),

а

также

законам

коммутативности,

ассоциативности

и

дистрибутивности.

a

a

...

a

11

12

1m

a21

a22

...

a2m

A

. . . .

an2

...

Шаг 4. Из матрицы инциденций

an1

anm

графа L ( X ,U ) , где n ,m соответственно равны числу вершин и рёбер графа, образуем матрицу Ax

a		x	a	x	...	a	x
	11	1	12	1		12	1
a21x2			a22 x2		...	a2m x2
Ax
	.		.		.	.
			an 2 xn		...
an1xn						anm xn

и составим произведение

44

						m	n
П		П		(x ,x	,...,x	) П	a x
	L		L	1 2	n	j 1i 1 ij i
Очевидно, что j-й сомножитель произведения								ПL есть сумма двух

слагаемых, соответствующих тем двум вершинам, которые в графе соединены j-м ребром.

Шаг 5. Преобразовать произведение ПL к бескобочному виду и

привести всю сумму к минимальной форме, пользуясь дистрибутивным,

ассоциа-тивным, коммутативным законами и применяя закон поглощения:

а) а+а b =а; б) (а+b)(а+с)…(а+р) = а+b с…р, где а, b, с,…, р -

логические переменные, принимающие значения 0;1, выполняя при этом условия, описанные в п.3.

В результате выполненных преобразований выражение ПL будет

иметь минимальную форму и представлять сумму произведений

переменных	из множества х1, х2, …,хi,…,хn , т.е. многочлен. Обозначим его
L .
Шаг	6. Для каждого слагаемого многочлена	L	выделим
переменные	которые в него не входят, но входят в множество { х1, х2,

…,хi,…,хn }. Эти переменные порождают максимальные пустые подграфы данного графа L, так как соответствующие им вершины графа L образуют максимальные пустые подграфы.

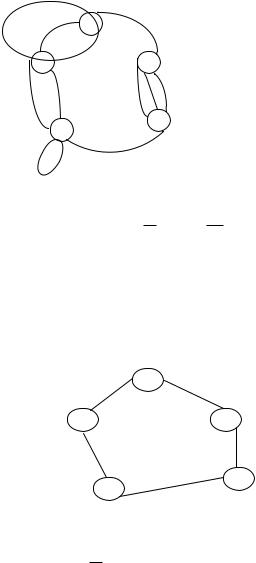
ПРИМЕР. В графе L (X ,U;P) , представленном на рисунке 5.1,

выделить все максимальные пустые подграфы.

45

	b
Матрица смежности B графа L содержит элементы	ij , i 1,5; j 1,5

,

равные: b11= b22= b33= b55=0; b44=1; b12=2; b13=1; b14 =0; b15 = 0; b21=2; b23=0; b24 =2; b25 = 0; b31=1; b32=0; b34 =0; b35 = 3;

b41=0; b42=2; b43 =0; b45 = 1; b51=0; b52=0; b53 =3; b54 = 1;

u1	1	u2
2		3
u4		u8 u

5

4

u7

Рисунок 5.1

Шаг 1. Строим скелет L (X ,U ) (рисунок 5.2) графа L .

u1	1	u2
2		3
u3		u4
4	u5	5

Рисунок 5.2

Шаг 2. Для графа L определим его матрицу инциденций А:

46

			u1		u2			u3			u4			u5
1			1		1			0			0			0
A 2			1		0			1			0			0
3			0		1			0			1			0
4			0		0			1			0			1
5			0		0			0			1			1

Шаг 3. Введём новые логические переменные х1, х2, х3, х4, х5 (по

числу вершин в графе L ) и из матрицы А образуем матрицу Ах :

				u1		u2			u3			u4			u5
	1			x1			x1		0			0			0
Ax	2			x2		0				x2		0			0
	3			0			x3		0				x3		0
	4			0		0				x4		0				x4
	5			0		0			0				x5			x5

Шаг 4. Составим произведение ПL

ПL (x1 x2)(x1 x3)(x2 x4)(x3 x5)(x4 x5)

Шаг 5. Преобразуем выражения ПL к минимальной форме:

ПL (x1 x2)(x1 x3)(x2 x4)(x3 x5)(x4 x5) =

(перемножаем скобки первую со второй и третью с пятой)

= (x1 x2 x3)(x4 x2 x5)(x3 x5) =

(перемножаем скобки первую со второй)

(x1x4 x1x2x5 x2x3x4 x2x3x5)(x3 x5) =

(перемножаем скобки первую со второй)

47

x1x3x4 x1x4x5 x1x2x3x5 x1x2x5 x2x3x4 x2x3x4x5 x2x3x5 x2x3x5

(применяем законы указанные в п.п. 3,5 данного пособия)

= x1x3x4 x1x4 x5 x1x2 x5 x2 x3x4 x2 x3x5 .

Преобразование выражения ПL закончено. Получена минимальная форма - полином L .

Шаг 6. Выделим для каждого слагаемого полинома

L	x x x x x x x x x x x x x x x
	=	1 3 4 1 4 5 1 2 5 2 3 4 2 3 5
его дополнение до множества переменных {x1,x2, x3, x4, x5}:
(x2x5);	(x2,x3); (x3,x4); (x1,x5); (x1,x4)

полученные дополнения порождают максимальные пустые подграфы графа

L , и заданного графа L .

Алгоритм Х.Магу и Дж. Уэйсмана может быть применён и для выявления в графе L=(X,U; P) общего вида всех максимальных полных подграфов. Для этого необходимо построить для заданного графа

L (X ,U;P) его скелет – граф

L ( X ,U ) , а для

графа L ( X ,U )

*

( X ,U

*

)

построить дополнительный

граф

L

(определение

дополнительного графа дано в теме 1 данного методического пособия).

Получить дополнительный граф легко, если исходный граф задать матрицей смежности его вершин, в которой всем элементам, равным нулю присвоить значение “1”, а всем элементам, значения которых не равны нулю присвоить значение “0”.

Далее для полученного графа L* ( X ,U *) с помощью алгоритма Х.Магу и Дж. Уэйсмана (рассмотренного выше) выявляем все

48

максимальные пустые подграфы. Эти подграфы являются максимальными

полными подграфами для графов L (X ,U ) и L (X ,U;P) .

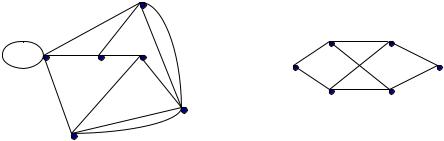
ПРИМЕР. В графе L (X ,U;P) , представленном на рисунке 1,

выделить все максимальные полные подграфы .

Шаг 1. Строим скелет L (X ,U ) (рисунок 5.2) графа L .

Шаг 2. Для графа L (X ,U ) строим его дополнительный граф

L* (X ,U	*)
	(рисунок 5.3), в котором с помощью алгоритма Х.Магу-
Дж.Уэйсмана выявляем				максимальные пустые
подграфы.			1
		u'1		u'2
	2		u'5	3
		u'3		u'4
	4			5

Рисунок 5.3

Приведём окончательный результат решения данной задачи -

полином

L = x1 x2 x3 x1 x2 x4 x1 x3 x5 x2 x4 x5 x3 x4 x5

и дополнения для его слагаемых: (x4 , x5 ); (x3, x5 ); (x4 , x2 ); (x1 , x3 ); (x1 , x2)

		49
которые	порождают все максимальные		пустые	подграфы			графа
L* (X ,U *)								)
		и максимальные полные подграфы графа			L	(X ,	U		и
заданного графа L (X ,U;P) .
Упражнения для самостоятельной работы
1.	Граф G задан матрицей смежности R 5 5 с элементами:
		r13 =2, r15 =1,
r23 =1, r24 =1, r31 =1, r32 =2, r34 =2, r35 =1, r42 =1, r43 =2, r51 =1, r53 =1.

Неуказанные элементы rij = 0.

Найти все максимальные пустые подграфы, с помощью алгоритма Х.Магу -Дж.Уэйсмана. Привести их геометрическое представление.

2. Построить скелет графа и дополнительный граф для графов,

представленных на рисунках 5.4, 5.5.

Рисунок 5.5

Рисунок 5.4

3. Найти все максимальные полные подграфы в графе,

представленном на рисунке 5.4.

50

4. Найти (аналитическим способом) число вершинного покрытия

0(G) для графа, представленного на рисунке 5.4.

5. Найти (аналитическим способом) число рёберного покрытия

1(G) для графа, представленного на рисунке 5.5.

6. Определить дополнение G графа G, если: а) G пятиугольник;

б) G треугольник.

ТЕМА 6. Раскраска графов

6.1. ПРАВИЛЬНАЯ РАСКРАСКА. ХРОМАТИЧЕСКОЕ ЧИСЛО

Под раскраской графа понимают приписывание его вершинам

(рёбрам) какого либо цвета.

Если в графе G = (X, U) его вершины (рёбра) раскрашены так, что смежные вершины (рёбра) окрашены в разные цвета, то такую раскраску называют правильной.

Если на правильную раскраску затрачено р цветов, то граф называется р - хроматическим.

Наименьшее натуральное число р, для которого граф является p-

хроматическим, называется хроматическим числом графа и обозначается

(G).

Для решения задачи правильной раскраски графа G=(X,U) и

определения его хроматического числа можно применить алгоритм Дж.

Магу, который подробно изложен в теме 5 (структурный анализ графов).

Раскраска графа с помощью алгоритма Дж. Магу выполняется в два

этапа.