Теория и техника передачи информации.-2

11

ных величин X (1) , X (2) ,..., X (n) , а от непрерывной случайной функции Y(t) – к системе Y (1) ,Y (2) ,...,Y ( n) . Полной статистической характеристикой сообщения и сигнала является 2 n -мерная совместная плотность вероятности W (x(1) ,..., x(n) , y(1) ,..., y( n) ) .

Для вычисления других характеристик необходимо использовать обобщение формул (1.3) – (1.8).

Помехи. Помехой называется всякое стороннее воздействие, мешающее правильному приему сигнала. Если принимае-

мый сигнал Y(t) связан с передаваемым сигналом		X (t) соот-
ношением
Y (t)	X (t) Q(t) ,	(1.9)
то помеха Q(t) называется аддитивной, а в случае
Y(t)	X (t)Q(t) -	(1.10)

мультипликативной.

В качестве помехи имеет смысл рассматривать только такую функцию Q(t) , значение которой заранее не известно по-

лучателю, так как в противном случае помеха может быть скомпенсирована в месте приема. Поэтому для описания помехи используют те же модели, что и для описания сигнала. Принципиальное отличие сигнала от помехи сводится к тому, что последняя не имеет информативных параметров.

РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ

Пример 1.1. Случайная величина X – число бросаний монеты до первого выпадания герба. Найти:

а) ряд распределения случайной величины X , б) математическое ожидание X ,

в) математическое ожидание двоичного логарифма вероятности X .

Решение. Возможные значения случайной величины X равны 1, 2, 3,... . Для осуществления события x n необходимо, чтобы в первых n -1 бросаниях выпадали решки, а в n-м броса-

нии выпал орел, поэтому p(x n) (1/ 2)n по формуле умножения вероятностей независимых событий. Ряд распределения

12

дан в табл. 1.1.

Таблица 1.1

xj	1	2	3	4	…
p(xj )	1/2	1/4	1/8	1/16	…

Математическое ожидание числа бросаний вычислим по формуле (1.2), положив

(x) x, m ,

M			X					x j		p(x j )			1			1			2			1				3		1	...
																2						4
					j 1																					8
	1				1						1						1						1				1					1				1		2
			(1 2					3				...)							(1										...)2										2.
2				2						4						2						2				4					2			1		0, 5
			Математическое ожидание двоичного логарифма вероятно-
сти			X	также								вычисляем										по					формуле							(1.2),				положив
	(x) log2							p(x) , т. е.
	M log2			p( X )								log2 p(x j ) p(x j )
												j 1
			log2	1					1			log2		1						1	...					1			1	2	1			3		1		... 2.
				2				2					4						4										2		4					8

Пример 1.2. По двоичному каналу связи с помехами (рис.

1.3) передаются сообщения x1		и x2	с априорными вероятностя-
ми p(x1 ) 0, 4 и p(x2 )	0, 6 . Влияние помех описывается пе-
реходными вероятностями:
p( y1 / x1 ) 0, 75 ,			p( y2 / x1 ) 0, 25 ,
p( y1 / x2 ) 0, 5 ,			p( y2 / x2 ) 0, 5 .
	Найти: а) безусловные вероятности
	сигналов на выходе канала;
	б)	наиболее		вероятное	значение
	X , если y		y1 ;
	в)	наиболее		вероятное	значение
	X , если y		y2 .
Рис. 1.3	Решение. Совместные вероятности

13

сообщения X и сигнала Y вычисляем по формуле умножения вероятностей (1.5):

p(x1, y1 )		p(x1 ) p( y1 / x1 )
0, 4	0, 75	0, 3,
p(x1 , y2 ) 0, 4 0, 25	0,1 ,	p(x2 , y1 ) 0, 6 0, 5 0, 3 ,

p(x2 , y2 ) 0, 6 0, 5 0, 3 .

Безусловные вероятности сигналов на выходе канала вычислим по формуле полной вероятности (1.3):

p( y1 ) p(x1, y1) p(x2 , y1) 0,3 0,3 0,6 ,

p( y2 ) p(x1, y2 ) p(x2 , y2 ) 0,1 0,3 0, 4 1 p( y1) .

Условные вероятности сообщений на входе находим по формуле Байеса (1.4):

	p(x1 / y1 )				p(x1, y1 )						0,3		0,5 ,
						p( y1 )			0, 6
	p(x2 / y1 )	0,3					0,5 1 p(x1 / y1 ) ,
		0, 6
	p(x1 / y2 )			p(x1, y2 )						0,1			0, 25 ,
					p( y2 )				0, 4
	p(x2 / y2 )	0,3					0, 75 1 p(x1 / y2 ) .
		0, 4
	Сравнив p(x1 / y2 )	и p(x2 / y2 ) , видим, что если принят

сигнал y2 , то более вероятно, что было передано сообщение x2 . Сигнал y1 мог быть с одинаковой вероятностью вызван сооб-

щениями x1 и x2 .

Пример 1.3. Сигнал Y(t) на выходе непрерывного канала связи выражается через входной сигнал X (t) соотношением Y (t) X (t) Z(t) , где Z (t) – аддитивный нормальный стационарный белый шум с односторонней спектральной плотностью

N	0	10	18 Вт/Гц, ограниченный полосой от 0 до F 10 МГц.
			B

Суммарная мощность составляющих в спектре сигнала X (t) ,

14

лежащих вне указанной полосы, пренебрежимо мала. Осуществить квантование по времени сигнала Y(t) на ин-

тервале от 0 до T 10 4 секунды. Для конкретной реализации входного сигнала (в вольтах)

		x(t)		10 6
			1 105 (t		5 10 5 )2
найти для квантованного сигнала:
	а) вектор условных математических ожиданий;
	б) условную корреляционную матрицу;
	в) условную плотность вероятности квантованного сигнала
на выходе.
	Решение. Чтобы осуществить квантование непрерывного
по	времени сигнала		Y(t) , необходимо взять его отсчеты
Y (1) ,Y (2) ,...,Y ( n)		в		моменты	времени		t	k	k t ,
k	1, 2,..., n , где	T	t n T t		1.

Верхняя граничная частота суммы сигнала с шумом равна FB , поэтому шаг квантования определяется в соответствии с теоремой Котельникова

			t	1		1	c 0, 05 мкс.
				2F		2 107
				B
Требуемое число отсчетов равно n 10 4 2 107 2000 .
Каждый отсчет сигнала Y (k )							Y (t	k	) является суммой двух
величин
				Y (k )		X (k )	Z (k ) ,
где X (k )	X (t	k	) - отсчет сообщения;
Z (k )	Z (t	k	) - отсчет шума.

Вектор условных математических ожиданий сигнала состоит из следующих элементов

m(k ) M Y (k ) / x(k ) x(k ) M Z (k ) x(k )

10 6

1 105 (5 10 8 k 5 10 5 )2

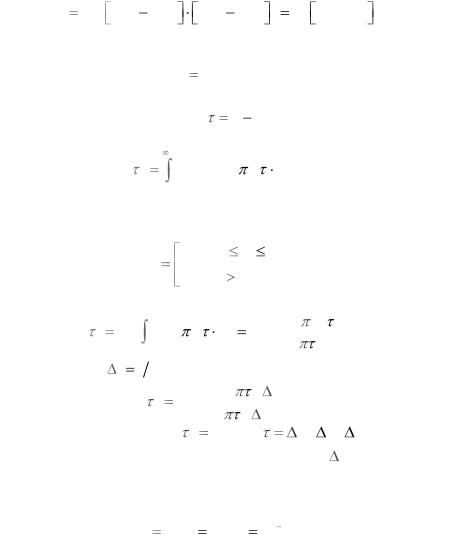
15

и определяется только передаваемым сообщением, так как математическое ожидание белого шума Z (t) равно нулю.

Условная корреляционная матрица B сигнала Y(t) при фиксированном x(t) состоит из следующих элементов

B(kj ) M Y (k ) m(k ) Y ( j ) m( j ) M Z (k ) Z ( j )

и равна корреляционной матрице отсчетов шума. Элементы этой матрицы есть отсчеты корреляционной функции шума

B(kj )

B(t

k

,t

j

) .

Шум стационарен, поэтому его корреляционная функция

зависит от разности аргументов

t1

t2

и может быть найдена

по теореме Винера – Хинчина

B(

)

G( f ) cos 2

f

df ,

0

где G( f ) – спектр плотности мощности шума.

По условию задачи, он равномерен в полосе 0… FB ,

G( f )

N0 ,

0

f

FB ,

0, f FB .

Находим выражение для корреляционной функции

FB

sin 2 FB

B( )

N0

cos 2

f

df

N0

.

2

0

Поскольку

t

1 (2FB ) , то

B( )

N

F

sin

/

t

.

0 B

/ t

Отсюда видно,

что

B(

)

0 при

t; 2 t;3 t,..., т.е.

отсчеты Z (1) ,..., Z (n) , взятые с шагом квантования t , некорре-

лированы. Таким образом, в корреляционной матрице отсчетов сигнала не равны нулю будут только элементы, стоящие на главной диагонали,

B(kk ) B(0) N F 10 11	,
0 B

16

численно равные дисперсии этих отсчетов (вольт2).

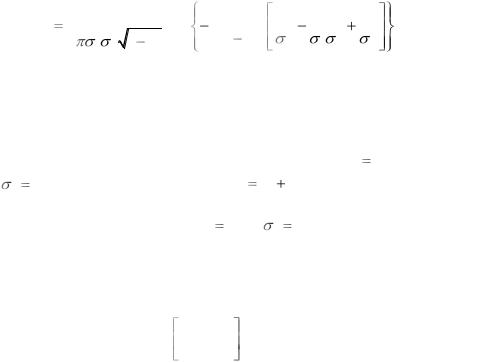
Условная плотность вероятности квантованного сигнала есть совместная плотность вероятности системы n некоррелированных (следовательно, и независимых) нормальных случайных величин

W y(1) ,..., y(n) / x(t)

n		1
k 1 2 B(kk )

1

(2 N0 FB )n2

	n
	W	y(k ) / x(k )
	k 1
	exp	1			( y	(k ) x(k ) )2
			2B(kk )
		1			n
	exp					( y(k ) x(k ) )2 .
		2N0 FB k 1

Пример 1.4. Доказать, что для любой положительной случайной величины X (имеющей только положительные возможные значения) при a 1 справедливо неравенство Иенсена

M loga X	loga M X .
Доказать, что для любой	системы	случайных величин
Q, L,..., Z и любой функции	, таких,	что (Q, L,..., Z) 0

при всех возможных значениях системы, справедливо аналогичное неравенство

M loga (Q, L,..., Z )	loga M (Q, L,..., Z ) .
Найти необходимые и достаточные условия, при которых
неравенства обращаются в равенства.
Решение. Сначала убедимся,	что непрерывная функция

y loga x является строго выпуклой вверх,									т.е. ее вторая про-
изводная отрицательна при любых x						0 .
Действительно,
y '	1	,	y "	1		1		0	при a 1.
	x ln a			ln a		x2
Следовательно, график функции						y		loga x лежит ниже ка-
сательной, проведенной в любой точке x0								0 (рис. 1.4):

17

	y loga x	loga x0		1		(x x0 ) ,
			x0 ln a
	причем знак	равенства		выполняется
	только в точке касания x				x0 .
	Предположим, что			X – положи-
Рис. 1.4	тельная случайная величина, тогда по-
	лученное неравенство справедливо для

любого из ее возможных значений и, следовательно, при усреднении обеих частей знак неравенства сохранится:

M loga

X

loga x0

1

M X

x0 .

x0 ln a

Выбрав

абсциссу

точки

касания

x0

M X ,

получим

окончательно

M loga X

loga M X .

Это неравенство обращается в равенство тогда и только то-

гда,

когда все

возможные

значения

случайной

величины

X

x0 M X

, т.е. если величина X не случайна.

Пусть случайная величина

X получена в результате функ-

ционального

преобразования

системы

случайных

величин

X

(Q, L,..., Z) 0 ,

тогда

в

силу доказанного неравенства

имеем

M

loga

(Q, L,..., Z )

loga M (Q, L,..., Z ) .

Это неравенство обращается в равенство тогда и только то-

гда, когда величина X

(Q, L,..., Z) не случайна.

ЗАДАЧИ

1.1В городе Н в 50% случаев бывает ясная погода, в 30% - переменная и в 20% - дождливая. Сообщения о погоде передаются при помощи кодовых слов «ясно», «переменно», «дождь». Найти среднее количество букв в одном кодовом слове (математическое ожидание длины кодового слова).

1.2В условиях задачи 1.1 сообщения о погоде передаются по линии связи при помощи импульсов амплитуды 5; З и 1 В

18

соответственно. Определить среднюю мощность в импульсе, если входное сопротивление линии равно 100 Ом.

1.3. В условиях задачи 1.2 на выходе линии связи установлен идеальный ограничитель сверху на уровне 0,5 В. Имеется ли статистическая зависимость сигналов на входе линии и выходе ограничителя?

1.4 Сообщение на входе линии связи может с одинаковой

вероятностью принимать одно из двух значений: x1		1 B или
x2	1 B. На выходе линии установлен вольтметр, ошибка из-

мерения которого распределена нормально с математическим ожиданием, равным нулю, и среднеквадратическим отклонением 0,5 В. Показание вольтметра в некоторый момент времени

равно 0,75 В. Найти условные вероятности сообщений x1 и x2 .

1.5Температура в камере может принять с одинаковой вероятностью любое значение в интервале от 0 до 40°. Как выбрать шаг квантования этой величины, чтобы ошибка квантования никогда не превышала 2°? Построить ряд распределения для квантованных значений температуры.

1.6В условиях задачи 1.5 найти средний квадрат ошибки квантования.

1.7Напряжение в сети в момент измерения - случайная величина, имеющая нормальное распределение с параметрами

m 220 В, 5 В. На интервале 190 - 240 В осуществить квантование этой величины с шагом u 5 В и построить ряд распределения.

1.8Сколько отсчетов по теореме Котельникова необходимо для передачи сигнала длительностью 10 мин с выхода микрофона, если спектр звуковых частот полностью заключен в полосе

20 - 20 000 Гц?

1.9Можно ли без искажений восстановить телевизионный видеосигнал, если по линии связи передавались его отсчеты с

шагом t 0, 2 мкс?

1.10 Система случайных величин XY имеет совместную плотность вероятности

19

W (x, y)

0,125, 0 x 2, 1 y 5,

0, вне этой области.

а) Вычислить четвертый центральный момент величины X . б) Являются ли эти случайные величины независимыми?

1.11Билеты лотереи, среди которых только один выигрышный, занумерованы числами от 0 до 999. Указать среднее количество цифр, необходимых для передачи номера выигравшего билета.

1.12По каналу связи передаются сообщения x1 или x2 с ве-

роятностями p(x1 ) 0, 7, p(x2 ) 0 ., 3Вследствие влияния помех сигнал на выходе может принимать одно из трех значений y1 , y2 или y3 с вероятностями:

p( y1 / x1 ) 0, 4 ,	p( y2 / x1 ) 0, 4 ,	p( y3 / x1 ) 0, 2 ,
p( y1 / x2 ) 0, 2 ,	p( y2 / x2 ) 0, 2 ,	p( y3 / x2 ) 0, 6 .

Найти вероятность ошибочных решений, если выходным сигналам ставить в соответствие следующие решения:

y1

x1 , y2

x1 ,

y3

x2 .

1.13 Даны математические ожидания двух нормальных слу-

чайных величин: mx

26 ,

my

12 и их корреляционная мат-

рица

K jk

91

.

196

91

169

Определить плотность вероятности системы XY , считая совместное распределение также нормальным.

1.14 Плотность вероятности системы трех случайных величин равна

W (x, y, z)		3				exp	1	2x2 4 y2 2 y(z 5) (z 5)2 .
			3				8
16		2

Найти совместную плотность вероятности величин X и Y . 1.15 Система случайных величин имеет нормальное рас-

пределение

20

W (x, y)

1

exp

1

x2

2rxy

y2

.

2(1 r

2

)

2

2

2 x y 1

r2

x

x y

y

Определить: а) условную плотность вероятности W (x / y) ,

б) условное математическое ожидание M X / y ,

в) условную дисперсию D X / y .

1.16 Сообщение

X

на входе линии связи есть случайная

величина,		имеющая нормальное		распределение с			mx 0	В,
x	10 В. Сигнал на выходе линии Y X					Z , где помеха Z -
случайная величина, независимая от X и имеющая нормальное
распределение с параметрами mz				0 В,		z 1 В. Указать наи-
более вероятное значение переданного сообщения							x , если сиг-
нал на выходе линии равен 7 В?
	1.17 Случайная величина X			может		принять одно из		m
значений		x1 , x2 ,..., xm . Какими		должны		быть	вероятности
p(xj ) , чтобы величина M ln			1		приняла наибольшее зна-
			p( X )

чение? Чему равно это значение?

1.18В двоичном симметричном канале с независимыми ошибками найти вероятность того, что в 1000-разрядной кодовой комбинации возникнет не более двух ошибок, если битовая

вероятность ошибки равна:

а) 10–2; а) 10–5.

1.19В двоичном симметричном канале с независимыми ошибками битовая вероятность ошибки равна 10–2. Оценить вероятность того, что в 1000-разрядной кодовой комбинации возникнет от 70 до 90 ошибок.

Указание. На основании центральной предельной теоремы теории вероятностей использовать аппроксимацию огибающей биномиального распределения колокольной кривой.

1.20Найти максимальное значение модуля ошибки квантования по уровню и ее среднеквадратическое значение, если шаг квантования равен 0,05 В.