ВОЕНЫ АЛЛАХА1АЗАЗАЗАЗ / 13_Теория_двойственности_сент_9_2008

О.А. Кашина, А.И. Кораблев

13. Элементы теории двойственности в линейном программировании

Пусть дана задача линейного программирования в симметричной форме записи

max c, x

Ax b

x 0.

(1)

Приведем определение еще одной задачи линейного программирования, тесно связанной с зада-

чей (1).

Определение

рования

при условиях

где вектор	y E
задаче (1).

1. Задача линейного программи-

min 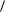b, y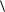

yA c , y 0 ,

m , называется двойственной к

В теории двойственности задачу (1) принято называть прямой. Легко убедиться, что задача, двойственная к двойственной, является прямой задачей линейного программирования. В связи с этим часто пару задач линейного программирования (прямую и двойственную к ней) называют

70

Методы оптимизации: Часть I

парой взаимосопряженных задач линейного программирования.

Пусть теперь прямая задача линейного программирования записана в канонической форме

max c, x
Ax b	(2)
x 0.

Тогда задача двойственная к (2) определяется следующим образом:

min 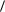b, y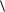

при условиях
yA c .
Многогранную область пространства	E	m	,

определяемую ограничениями двойственной зада-

чи, будем обозначать	D .
Следующие три	теоремы устанавливают

свойства взаимосопряженных задач линейного программирования, вытекающие непосредственно из их определения.

Теорема 1. Пусть дана пара взаимосопряженных задач линейного программирования в

симметричной форме,	векторы	x D	и	y D .
Тогда
c, x	b, y .			(3)

Доказательство. Легко увидеть, что из ограничений прямой и двойственной задач линейного программирования следуют неравенства:

71

О.А. Кашина, А.И. Кораблев

c, x

yA, x

b,

y

.

Из них и получаем неравенство (3).

Теорема 2. Пусть дана пара взаимосопряженных задач линейного программирования в

симметричной	форме,	векторы	x D	и	y D
таковы, что
	c, x	b, y .			(4)
Тогда векторы	x, y являются		решениями,		соот-

ветственно, прямой и двойственной задач линей-

ного	программирования.
	Доказательство.			Из теоремы 1		следует,		что
c, x		b, y	для любого		x D . Отсюда и		из	ра-
венства		(4)	имеем	c, x	c, x	для	любого
x D .		Таким образом,		x – решение прямой зада-

чи линейного программирования. Второе утверждение теоремы доказывается аналогично.

	Теорема 3.	Для	того, чтобы множество					D
было пустым, достаточно,				чтобы функция			b, y
была	неограниченна		снизу	на	множестве		D	.
	Справедливость		этого	утверждения следует
непосредственно		из	теоремы 1.
	Очевидно, что утверждение теоремы 3 в
применении к		двойственной			задаче	принимает
вид:
	Для того, чтобы множество D					было пус-
тым,	достаточно,		чтобы	функция		c, x	была
72

Методы оптимизации: Часть I

неограниченна сверху на множестве

D

.

Теорема 4. (Теорема двойственности) Пусть одна из пары взаимосопряженных задач линейного программирования в симметричной форме имеет решение. Тогда и двойственная к ней задача тоже имеет решение и для любых векторов

	*
x	D

и

y		D	*	выполняется		равенство
			c, x		b, y .	(5)

Доказательство. Пусть имеет решение прямая задача линейного программирования. Тогда

из теоремы 11.4 следует, что найдется такой век-
тор	y 0 , что вектор	x , y – седловая точка

функции Лагранжа

		, y
L x	, y L x

прямойL x, y

задачи. Таким образом,при всех x 0, y 0 .

Отсюда, Лагранжа

получаем

	c, x

учитывая то, что для задачи (1) функция

имеет

вид

L(x, y) c, x

y,

Ax b

,

неравенства

c, x

y, Ax

b

, Ax

b

c, x

, Ax b

при

y

y

всех b, y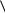

x 0, y 0

. Перепишем их в виде

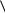
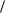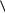
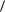x, c y Ab, y x , c y Ab, y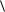

	x , c yA	при всех	x 0 , y 0 . Отсюда,		так
как	функция	Лагранжа	для	двойственной задачи
имеет вид L y, x b,			y	x, c yA , получаем
L y , x L y , x L y, x , y 0, x 0 .					По-
					73

О.А. Кашина, А.И. Кораблев

следние неравенства означают, что вектор

y		,	x

является седловой точкой функции Лагранжа для двойственной задачи. Тогда из теоремы 11.4 следует, что вектор y – решение двойственной

задачи линейного программирования.

Для доказательства второго утверждения

теоремы выберем точки

x	D

и

	D
y

*

. Так

как	x		– решение прямой задачи, то	по
11.4	существует вектор y 0 такой,			что

теореме

x , y –

седловая точка функции Лагранжа прямой задачи.

Следовательно, как доказано выше,					,
выполняется условие	%y, Ax		b	0

y D * и

то есть

%y,	Ax			b,

%y

.

С другой стороны, аналогично,

вектор

y,	x

– седловая точка функции Лагран-

жа двойственной задачи, а значит, выполняется

условие

x		, c

%yA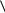

0

, то есть

%yA, x

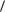c,

x

.

Таким образом,

c, x

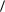b,

%y

.

Откуда, учитывая,

что 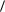b, %y b, y 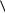, получаем равенство (5). Что и требовалось.

Заметим, что все результаты этого параграфа были изложены применительно к задачам линейного программирования в симметричной форме. Аналогичные утверждения справедливы и для задач в других формах записи с небольшими изменениями, связанными только лишь с конкретной формой.

74

Методы оптимизации: Часть I

Подводя итоги полученным в этом параграфе результатам, можно сделать вывод, что имеет место одна из следующих ситуаций:

–обе взаимосопряженные задачи линейного программирования имеют решения;

–обе задачи не имеют решений, так как

целевая функция одной из задач неограниченна на допустимой области, а допустимая область двойственной к ней задачи пуста;

– обе задачи не имеют решений, так как их допустимые области пусты.

75