
Лекции / Matematika (3)
.pdf
Математика
Вопрос 1.
Функция одной переменной:
Если заданы множества X и Y, а так же правило f, по котором для каждого x из множества X, можно определить единственное число y из множества Y, то говорят, что из множества X задана функция f.(x- аргумент; y- функция от x; f- функциональная зависимость; D(f) – множество X; E(f) – множество Y)
Способы задания функции:
Табличный – зависимость y от x задаётся в виде таблицы.
Словесный
Аналитический (формула)
Графический - в системе координат на плоскости изображается множество точек с координатами
(x;f(x))
Сложная функция:
Если к каждому действительному числу x из области определения можно сначала применить основную элементарную функцию , а затем к результату применить функцию f, то получим единственное значение y:
= [ ( )]
В составлении сложной функции может участвовать и более двух основных элементарных функций. Последняя из цепочки основных элементарных функций называется внешней функцией, а предыдущие - вложенными функциями. Представление сложной функции с помощью цепочки основных элементарных правил называют композицией.
Элементарная функция:
Функция, полученная из основных элементарных функций путём выполнения конечного числа операций сложения, вычитания, умножения, деления и композиции функции.
Неэлементарные функции:
Кусочно заданная функция:
( ) = { 1( ), 12( ), 2
− 2, |
−3 < ≤ 5 |
||
Пример: ( ) = { 1 |
, |
> 5 |
|
|
|
||
|
|
||
Неявно заданная функция:
( , ) = 0
Пример: + − cos( ) + 1 = 0
Параметрически заданная функция:
= ( )
= ( ): { = ( )
Пример: { = 2
= cos( )
Степенно-показательная функция:
= [ ( )] ( )
Пример: = sin( )
Основные элементарные функции:
Постоянная функция
= , =
Степенная функция:
= , , ( ) =
1= , , ( ) = (кроме 0)
1
= , , ≠ 1
Показательная функция:
= , > 0, ≠ 1, ( ) =
Логарифмическая функция:
= log , > 0, ≠ 1, ( ) (0;+∞)
Тригонометрическая функция:
= sin( ) , ( ) =
= cos( ) , ( ) =
= ( ) , ( ) = (− 2 + ; 2 + ) ,
= ( ), ( ) = ( ; + ),
Обратные тригонометрические функции:
= arcsin( ) , ( ) [−1; 1]
= arccos( ), ( ) [−1; 1]
= ( ), ( ) =
= ( ), ( ) =
Вопрос 2.
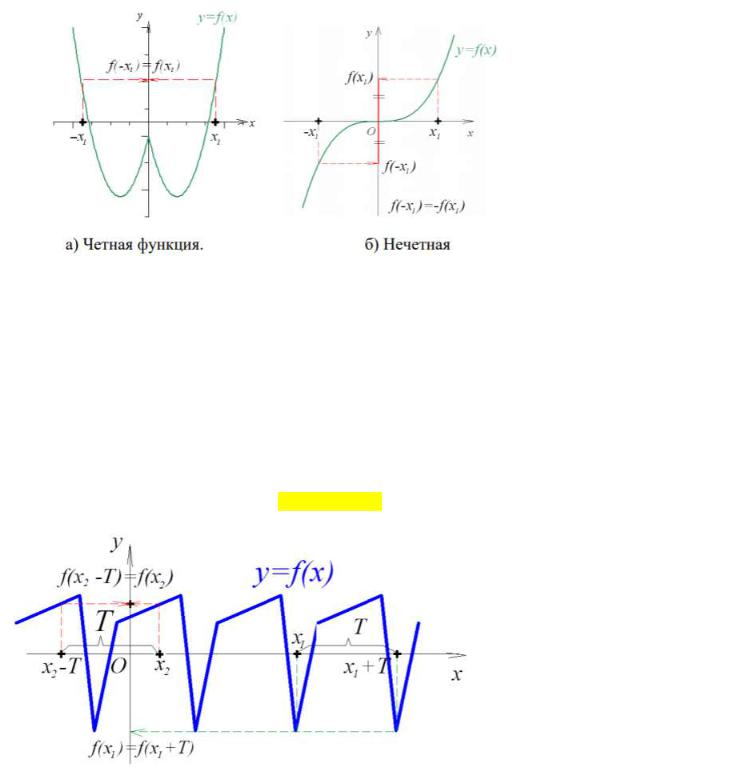
Чётность:
Функция = ( ) называется чётной, если для любого значения аргумента из области определения найдется значение (− ) в области определения и для них выполняется равенство (− ) = ( )
Функция = ( ) называется нечётной, если для любого значения аргумента из области определения найдется значение (− ) в области определения и для них выполняется равенство
(− ) = − ( )
Функцию, не являющуюся ни четной, ни нечетной, называют функцией общего вида.
Примеры:
1.= 2- чётная, т.к (− ) = (− )2 = 2 = ( )
2.= 3-нечётная, т.к (− ) = (− )3 = − 3 = − ( )
Периодичность:
Функция = ( ) называется периодической с положительным периодом , если для любого значения аргумента из области определения точки ( ± ) принадлежат области определения функции и значения функции совпадают во всех трех точках, т.е ( ± ) = ( )
Примеры:
= cos( )
= ( )
= (−1) ,

Вопрос 3.
Ограниченность:
Функция = ( ) называется ограниченной снизу на промежутке ( ) , если найдется такое
действительное число 1, что для любого значения аргумента из области определения выполняется условие ( ) ≥ 1 , а если не найдется, то функция называется неограниченной снизу на . Обозначается: = ( ) на
Функция = ( ) называется ограниченной сверху на промежутке ( ) , если найдется такое действительное число 2, что для любого значения аргумента из области определения выполняется условие ( ) ≤ 2 , а если не найдется, то функция называется неограниченной сверху на .
Обозначается: = ( ) на
Если функция ограничена и сверху и снизу на , она называется ограниченной на и обозначается
= ( ). Неограниченной на будем называть функцию, которая на этом промежутке не ограничена
ни сверху, ни снизу.
Примеры:
Ограничена снизу: = 2 − 5 + 12 Ограничена сверху: = −2 + 6 Ограничена сверху и снизу: = cos( ) Не ограничена: = 2

Вопрос 4.
Предел функции в точке:
Предел элементарной функции в точке из области определения равен значению функции в этой точке:
lim ( ) = ( ), где = ( ) и ( )
→
Из теоремы следует:
Она верна и для основных элементарных функций
Любой многочлен ( ) = 0 + 1 + 2 2 + +
в любой точке всегда имеет конечный предел, т.к. он
является элементарной функцией и ( ) =
Основные свойства конечных пределов функции в точке:
Пусть существуют конечные пределы lim ( ) = и
→
lim ( ) = , тогда справедливы следующие свойства:
→
Примеры: |
|
|
1) lim( 2 |
+ 2 ) = lim 2 + lim2 = 12 + 2 ∙ 1 = 3 |
|
→1 |
→1 |
→1 |
2) lim 4 = 4
→4
3) lim( + 1) sin = lim( + 1) ∙ lim sin = (0 + 1) ∙ sin 0 = 0
→0 |
→0 |
→0 |

Вопрос 5.
Бесконечно малая функция в точке:
Если предел функции = ( ) в точке = равен нулю, то функция называется бесконечно малой в этой точке:
[ ( ) − б/м] lim ( ) = 0 |
|
→ |
→ |

Примеры применения свойств: |
|
|
|
|
|
|
|
||||||||||||
1) |
lim 2 + = lim 2 |
+ lim = [б/м + б/м = б/м] = 0 |
|||||||||||||||||
|
→0 |
|
|
|
|
→0 |
→0 |
|
|
|
|
|
|
||||||
2) |
lim( − 3)( 2 + 4) = lim( − 3) ∙ lim( 2 + 4) = [б/м ∙ ( ( ) → ) = б/м] = 0 |
||||||||||||||||||
|
→3 |
|
|
|
|
|
|
|
|
→3 |
|
|
→3 |
|
|||||
3) |
lim |
−6 |
|
= [ |
|
|
б/м |
|
|
= б/м] = |
|
0 |
= 0 |
||||||
2+3 |
( ( )→ )≠0 |
36+3 |
|||||||||||||||||
|
→6 |
|
|
|
|
|
|
||||||||||||
Неопределённость вида [ |
|
]: |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если рассматривается предел дроби lim |
( ) |
, у которой в числителе и знаменателе бесконечно малые |
|||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ ( ) |
|
|
|||
|
|
|
|
( |
) |
|
|
|
|
|
( |
) |
= 0), то говорят, что под знаком предела задана неопределенность |
||||||
функции (т.е. lim |
|
= 0 и lim |
|
||||||||||||||||
|
|
→ |
|
|
|
|
|
→ |
|
|
|
|
|
|
|
||||
«ноль на ноль» [00].
Способ раскрытия неопределённости вида [ ]:
lim |
( ) |
0 |
] = lim |
( − ) ∙ |
( ) |
|
|
= [ |
−1 |
|
( ) |
||
→ ( ) |
0 |
→ ( − ) ∙ |
|
|||
|
|
|
|
−1 |
|
|
1)Многочлены можно разложить на множители, среди которых обязательно есть ( − ). После сокращения дроби чаще всего числитель или знаменатель уже не будет бесконечно малым. Тогда говорят, что «неопределенность раскрыта» и находят предел.
Для разложения на множители используют формулы сокращенного умножения и формулу:
2 + + = ( − 1)( − 2), где 1, 2 − корни многочлена 2 + +
2)Если под знаком предела неопределенность [ ] связана с иррациональностями, то раскрыть ее может помочь домножение числителя и знаменателя дроби на сопряженный множитель, который дополняет выражение до разности квадратов или кубов. Например:
(√ − √ ) сопряжен с (√ + √ ), т.к. (√ − √ )(√ + √ ) = −
(3√ + 3√ ) сопряжен с ((3√ )2 − 3√ 3√ + (3√ )2), т.к. (3√ + 3√ ) ((3√ )2 − 3√ 3√ + (3√ )2) = +
Примеры:
|
|
|
4 2+11 −3 |
0 |
|
|
|
|
|
( +3)(4 −1) |
|
|
4 −1 |
|
|
4(−3)−1 |
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1. |
lim |
( |
|
|
|
|
|
) = [ |
|
] |
= lim |
( |
|
|
|
|
|
) = lim |
|
|
|
= |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2−9 |
|
|
|
|
( +3)( −3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
→−3 |
|
|
|
|
|
0 |
|
→−3 |
|
|
|
→−3 |
−3 |
|
|
−3−3 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2. |
lim √ +8−3 = |
[ |
0 |
] = lim |
(√ +8−3)(√ |
|
+8+3) |
= lim |
|
−1 |
|
|
|
= lim |
|
|
1 |
|
|
= |
1 |
|
|
= |
1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
→1 |
−1 |
0 |
|
→1 |
( −1)(√ +8+3) |
→1 |
( −1)((√ +8+3)) |
→1 |
√ +8+3 |
|
√1+8+3 |
|
6 |
||||||||||||||||||||||||||||||

Вопрос 6.
Сравнение бесконечно малых функций:
|
lim |
( ) |
= = ≠ 0 |
( |
) |
и ( ) называются бесконечно малыми функциями одного |
|
||||||
|
|
|
|
|||
|
→ ( ) |
|
|
|
|
|
порядка малости в точке = и обозначается ( ) ( )
lim ( )( ) = 0 говорят, что ( ) более высокого порядка малости в точке = , чем ( )→
Символически: ( ) ( )
lim ( )( ) = ∞ говорят, что ( ) более низкого порядка малости в точке = , чем ( )→
Символически: ( ) ( )
lim ( )( ) = 1 ( ) и ( ) называются эквивалентными бесконечно малыми функциями в точке→
= и обозначаются ( ) ~ ( )
Примеры:
Доказательство эквивалентности (на 2-х примерах):
1) Докажем, что − ~ , →
Доказательство:
|
|
|
2( |
1−cos |
) |
|
|
|
2 |
|
|
|
2 |
|
|
|
lim |
1−cos |
2 |
= lim |
(sin2) |
|
lim ( |
sin2 |
) |
= 1 |
2 |
= 1 |
|||||
|
2 |
= lim |
|
2 |
|
|
2 |
|
|
|
||||||
→0 |
|
→0 |
|
|
→0 |
|
|
|
|
|
|
|
|
|||
2 |
2∙ 4 |
|
4 |
|
2→0 |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
2)Докажем, что ( + )~, →
Доказательство:
lim ln(1 + ) |
|
|
1 |
1 |
|
= lim |
1 ln(1 + ) = lim ln(1 + ) |
= ln(lim(1 + ) ) = ln = 1 |
|||
→0 |
|
→0 |
|
→0 |
→0 |

Вопрос 7.
Бесконечно большая функция в точке:
Если предел функции = ( ) в точке = стремится к бесконечности, то функция называется бесконечно большой в этой точке:
[ ( ) − б/б] lim ( ) = ∞ |
|
→ |
→ |
Свойства бесконечно больших функций:
б/б + б/б = б/б (если б/б – одного знака)
б⁄б ∙ б⁄б = б⁄б , в том числе (б⁄б) = б⁄б ,
б⁄б ± ( ( ) → ) = б⁄б, в том числе б⁄б ± = б⁄б
б/б ± б/м = б/б
б⁄б ∙ ( ( ) → ≠ 0) = б⁄б, в том числе б⁄б ∙ ( ≠ 0) = б⁄б
|
б⁄б |
|
⁄ |
б⁄б |
|
( )→ ≠0 |
= б б, в том числе |
≠0 |
|
бб⁄⁄мб = б⁄б
( )→ = б⁄м , в том числе = б⁄м
б⁄б б⁄б
бб⁄⁄мб = б⁄м
( )→ ≠0 = б⁄б, в том числе ≠0 = б⁄б
б⁄м б⁄м
Примеры применения свойств:
|
|
|
|
ln |
|
|
|
б⁄б<0 |
|
|
|
⁄ |
|
|
|
|
|
|
|
|
|||
1) |
lim |
|
|
|
= [ |
б⁄м>0 |
= б б < 0] = −∞ |
|
|
|
|
|
|||||||||||
|
→0 sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
lim |
|
= [ |
( )→ |
= б/м] = 0 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
→ |
|
|
|
|
б/б |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
≠0 |
( ( |
) |
|
) |
⁄ ( ( ) |
|
) |
⁄ |
|||
3) |
lim |
( |
|−3| |
+ ) = |
[ |
б⁄м |
|
+ |
|
→ |
|
= б б + |
→ |
|
= б б] = ∞ |
||||||||
|
→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

Вопрос 8.
Бесконечно большая функция на бесконечности:
Функция может быть бесконечно большой на бесконечности при → ∞, т.е. lim ( ) = ∞
→∞
lim √ = [ − нечётн. ] = ±∞
→±∞
lim √ = [ − чётн. ] = +∞
→+∞
Свойства функций, бесконечно больших в точке, сохраняются и на бесконечности:
б/б + б/б = б/б (если б/б – одного знака)
б⁄б ∙ б⁄б = б⁄б , в том числе (б⁄б) = б⁄б ,
б⁄б ± ( ( ) → ) = б⁄б, в том числе б⁄б ± = б⁄б
б/б ± б/м = б/б
б⁄б ∙ ( ( ) → ≠ 0) = б⁄б, в том числе б⁄б ∙ ( ≠ 0) = б⁄б
|
б⁄б |
|
⁄ |
б⁄б |
|
( )→ ≠0 |
= б б, в том числе |
≠0 |
|
бб⁄⁄мб = б⁄б
( )→ = б⁄м , в том числе = б⁄м
б⁄б б⁄б
бб⁄⁄мб = б⁄м
( )→ ≠0 = б⁄б, в том числе ≠0 = б⁄б
б⁄м б⁄м
Если функция не имеет конечного предела на бесконечности, хотя и существует на R, но при этом ограничена, то:
|
|
|
|
|
|
б⁄б ∙ ( ) = б⁄б |
|||||
|
б⁄б |
|
|
|
|
= б⁄б |
|||||
|
|||||
( ) |
|||||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
( )б/б = б⁄м
Примеры применения свойств:
|
cos |
|
( ) |
⁄ |
1) lim |
|
= [ |
|
= б м] = 0 |
|
|
|||
|
|
|||
→∞ 3+ |
|
б⁄б |
|
|

2)lim 2 + 2 = lim 2 + lim 2 = [б⁄б + б⁄б = б⁄б] = ∞
→∞ |
→∞ |
→∞ |
3)lim 3 + 10 = lim 3 + lim 10 = [б⁄б < 0 + = б⁄б < 0] = −∞
→−∞ |
→−∞ |
→−∞ |
Вопрос 9.
Бесконечно большая функция на бесконечности: см. Вопрос 8 ↑
Раскрытие неопределённости [∞∞]:
Чтобы раскрыть неопределённость вида [∞∞] необходимо разделить числитель и знаменатель дроби на степень , тогда в общем виде:
|
|
|
|
|
|
|
2 |
|
|
|
0, при < |
||
lim |
( ) |
= lim |
|
|
+ + |
+ + |
= [ |
|
|
, при = |
|||
|
|
0 |
1 |
2 |
|
|
|
|
|||||
→∞ ( ) |
→∞ + + 2 |
+ + |
|
|
|
||||||||
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
∞, при > |
||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
3 |
|
5 |
|
|
||||
2 2 |
− 3 + 5 |
|
∞ |
|
2 − |
2 |
+ |
|
|
2 |
||||||
= [ |
] = |
2 |
|
|||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||
|
|
|
∞ |
1 |
|
3 2 |
3 |
|||||||||
→∞ 1 + + 3 2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
+ |
|
+ |
2 |
|
|
|||
|
|
|
|
|
|
|
2 |
2 |
|
|
||||||
Раскрытие неопределённости [∞ − ∞]:
Чтобы раскрыть неопределённость вида [∞ − ∞] можно вынести общий множитель
Пример: lim |
( |
|
1 |
− |
3 |
|
) = |
[∞ − ∞] |
= lim |
( |
1 |
− |
3 |
) = lim ( |
( 2+ +1)−3 |
) = |
||||
|
2− |
|
|
|
( −1)( 2+ +1) |
( −1)( 2+ +1) |
||||||||||||||
|
→1 |
|
|
|
|
3−1 |
|
→1 |
|
( −1) |
|
→1 |
|
|||||||
= lim ( |
( −1)2 |
|
) = lim ( |
−1 |
) = |
0 |
= 0 |
|
|
|
|
|
||||||||
|
|
|
|
|
( 2+ +1) |
|
|
|
|
|
|
|||||||||
→1 |
( −1)( 2+ +1) |
|
→1 |
|
3 |
|
|
|
|
|
|
|
|
|||||||
Чтобы раскрыть неопределённость вида [∞ − ∞], кроме вынесения общего множителя используют умножение на сопряженный множитель
|
|
|
|
|
|
|
|
|
|
|
|
|
(√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2+1−√ 2−1)(√ 2+1+√ 2−1) |
|
|||||||||
Пример: |
lim (√ 2 |
+ 1 − √ 2 − 1) = [∞ − ∞] = lim ( |
) = |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
√ 2+1+√ 2−1 |
|||||||||||||||||||||
|
|
|
→∞ |
|
|
|
|
|
→∞ |
|
|
|
|||||||||||
= lim ( |
|
|
2 |
|
|
) = |
| |
|
= б⁄м| = 0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
→∞ |
√ 2+1+√ 2−1 |
|
|
б/б |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
