Лекции / 2-3

(лево)сторонние пределы функции в точке оказываются бесконечными, то говорят, что функция в этой точке бесконечно большая справа (слева).

Заметим, что:

•если в точке равны односторонние пределы функции, то в ней существует общий предел; например, на рисунке

,

аналогично и ;

•если в точке односторонние пределы не совпадают, то общего предела в ней нет; например, на рисунке

, т.е. .

Теор.: Предел элементарной функции в точке из области определения равен значению функции в этой точке:

Из теоремы следует, что:

•она верна и для основных элементарных функций;

•любой многочлен в любой точке всегда имеет конечный предел, т.к. он является элементарной функцией и .

1.1.Найдите .

Основные свойства конечных пределов функции в точке

Пусть существуют конечные пределы и , тогда справедливы следующие свойства:

1) ; в том числе, .

2) ;

3) ;

4) , если ;

5) , если ;

6) ;

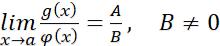7) для сложной функции ;

8) , если такая степень существует;

9)Функция не может иметь в точке более одного предела. Он либо единственный, либо не существует.

1.2.Найдите пределы:

а) ; б) .

§ 2.Бесконечно малая функция в точке

Опр.: Если предел функции в точке равен нулю,

то функция называется бесконечно малой в этой точке:

2.1. Является ли функция бесконечно малой в точках: а) ; б) ?

Некоторые свойства бесконечно малых функций

• ;

, где - окрестность точки ,

т.е. любой интервал, содержащий точку ;

•Произведение бесконечно малой в точке функции на

бесконечно большую в этой точке может быть как

бесконечно малой, так и бесконечно большой, или иметь другой конечный предел, поэтому оно называется

неопределенностью «ноль на бесконечность» и

обозначается 0 .