Вопросы по ВиТа (Матанализу)

1. Собственные интегралы, зависящие от параметра.

Теоремы о непрерывности (с доказательством), дифференцируемости и интегрируемости.

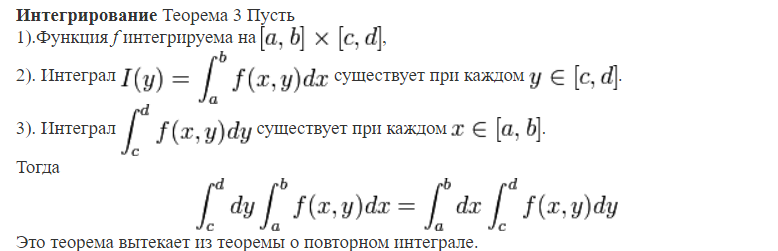
Правило Лейбница нахождения производной.

Примеры.

2. Несобственные интегралы, зависящие от параметра.

Равномерная сходимость, признаки равномерной сходимости (признак Вейерштрасса с доказательством).

Примеры.

3. Несобственные интегралы, зависящие от параметра.

Теоремы о непрерывности, дифференцируемости и интегрируемости.

Примеры.

4. Эйлеровы интегралы: гамма-функция и ее свойства (7 утверждений). Примеры.

Гамма-функция Эйлера Γ(x) (эйлеров интеграл второго рода) определяется как несобственный интеграл Γ(x)=+∞∫0tx−1e−tdt, x>0 с двумя особыми точками, t=0 и t=+∞.

Для того чтобы можно было применить теоремы об интегралах, зависящих от параметра, представим интеграл (1) в виде суммы двух интегралов Γ(x)=1∫0tx−1e−tdt++∞∫1tx−1e−tdt. Оба интеграла сходятся равномерно по параметру x на любом конечном отрезке [a,b]⊂(0,+∞) по признаку Вейерштрасса. Действительно, пусть 0<a<1, b>1. Тогда 0≤tx−1e−t≤ta−1 при x≥a, 0≤t≤1 и 1∫0ta−1dt=a−1. Следовательно, интеграл 1∫0tx−1e−tdt сходится равномерно на [a,b].

Аналогично 0≤tx−1e−t≤tb−1e−t при x≤b, t≥1, интеграл +∞∫1tx−1e−tdt сходится, а интеграл +∞∫1tx−1e−tdt сходится равномерно на [a,b].

Так как подынтегральная функция tx−1e−t непрерывна при t>0, x>0, то в силу теоремы 4 отсюда оба интеграла в формуле (2) будут непрерывными функциями параметра x на произвольном отрезке [a,b]⊂(0,+∞), а поэтому Γ(x) есть непрерывная функция при x>0.

При x>0 функция Γ(x) непрерывно дифференцируема, причем Γ′(x)=1∫0tx−1e−tlnt dt++∞∫1tx−1e−tlnt dt=+∞∫1tx−1lnt e−tdt. Дифференцирование под знаком интеграла законно, так как оба интеграла в формуле (3) сходятся равномерно по параметру x на любом отрезке [a,b]⊂(0,+∞).

По индукции можно доказать, что Γ(x) есть бесконечно дифференцируемая функция при x>0 и Γ(n)(x)=+∞∫0tx−1e−t(lnt)ndt. В частности, Γ″(x)=+∞∫0tx−1e−t(lnt)2dt>0. Поэтому Γ(x) — выпуклая вниз функция при x>0 и имеет единственный положительный минимум. Нетрудно было бы показать, что формула (3) имеет место и для комплексных x при Re x>0, и поэтому Γ(x) есть регулярная функция комплексной переменной x в правой полуплоскости Re x>0.

Выведем теперь основное функциональное соотношение для гамма-функции. Пусть x>0. Интегрируя по частям, находим Γ(x+1)=+∞∫0txe−tdt=−e−ttx|+∞0+x+∞∫0tx−1e−tdt=xΓ(x),Γ(x+1)=xΓ(x), x>0.

Это и есть основное функциональное соотношение для гамма-функции, найденное Эйлером. На нем в значительной мере основана теория гамма-функции.

Прежде всего заметим, что если x∈(0,1], то x+1∈(1,2]. Поэтому, зная значения Γ(x) на промежутке (0,1], можно при помощи формулы (5) найти значения Γ(x) на промежутке (1,2], а следовательно, и на любом отрезке [n,n+1], n=1,2,… Это существенно облегчает вычисление значений гамма-функции.

Далее, формула (5) позволяет исследовать поведение Γ(x) при 

x→+0x→+0. Имеем

Γ(x)=Γ(x+1)x∼Γ(1)x при x→+0,Γ(x)=Γ(x+1)x∼Γ(1)x при x→+0,

так как Γ(x+1)Γ(x+1) — непрерывная функция при x=0x=0, а Γ(1)=∫0+∞e−tdt=1Γ(1)=∫0+∞e−tdt=1. Таким образом, Γ(x)→+∞Γ(x)→+∞ при x→+0x→+0.

Из формулы (5)(5) находим

Γ(n+1)=nΓ(n)=n(n−1)…1⋅Γ(1)=n!.Γ(n+1)=nΓ(n)=n(n−1)…1⋅Γ(1)=n!.

Функция n!n! определена для натуральных nn. Гамма-функция Γ(x)Γ(x) непрерывна для всех x>0x>0 и Γ(n+1)=n!Γ(n+1)=n!.

Формула (5)(5) позволяет продолжить функцию Γ(x)Γ(x) с сохранением ее свойств на отрицательные значения xx, не равные −1,−2,…,−n,…−1,−2,…,−n,…

Положим по определению

Γ(x)=Γ(x+1)x, −1<x<0.(6)(6)Γ(x)=Γ(x+1)x, −1<x<0.

Так как при x∈(−1,0)x∈(−1,0) имеем x+1∈(−1,0)x+1∈(−1,0), то определение (6) корректно. Исследуем поведение Γ(x)Γ(x) при x→−1+0x→−1+0. Полагая y=x+1y=x+1, получаем, что x→−1+0x→−1+0 эквивалентно y→+0y→+0. Поэтому при y→+0y→+0, используя (6), получаем

Γ(y−1)=Γ(y)y−1∼−Γ(y)∼−1y=−1x+1.Γ(y−1)=Γ(y)y−1∼−Γ(y)∼−1y=−1x+1. Итак,

Γ(x)∼−1x+1, x→−1+0.Γ(x)∼−1x+1, x→−1+0.

По индукции теперь можно определить Γ(x)Γ(x) на любом интервале (−(n+1),−n)(−(n+1),−n), где n∈Nn∈N, формулой Γ(x)=Γ(x+1)xΓ(x)=Γ(x+1)x, x∈(−(n+1),−n)x∈(−(n+1),−n), причем Γ(x)∼(−1)nx+nΓ(x)∼(−1)nx+n при x→−nx→−n.