Лаб 3 / Отчет 3

Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования

Национальный исследовательский университет “МИЭТ”

Факультет Прикладных информационных технологий

Отчет по лабораторной работе №3

Вариант 7

Дисциплина: Численные методы

Выполнил:

Студент П-43

Губарев Сергей

Москва, 2022 год

Метод простой итерации решения СЛАУ

Цель работы: изучение задачи численного решения систем линейных алгебраических уравнений (СЛАУ); приобретение навыков программирования итерационных методов решения СЛАУ; приобретение навыков использования стандартных средств системы Matlab для решения СЛАУ.

Ход работы

1. С помощью программы сгенерировать матрицу A и вектор правых частей b для СЛАУ вида Ax=b.

2. Проверить условия сходимости итерационных методов для матрицы A. При необходимости преобразовать матрицу A к виду, позволяющему вычислить решения.

3. Вычислить решения с помощью метода простой итерации и Зейделя, количество итерации n = 20. Построить графики зависимости xi от n. Вычислить вектор невязки решения и ее норму.

4. Получить точное решение СЛАУ, вычислить вектор погрешности решений по методам простой итерации, Зейделя и их нормы.

5. Оценить относительную погрешность решения СЛАУ, если ∆A определяется десятипроцентным увеличением диагональных элементов, а ∆b таким же уменьшением всех элементов.

% Задача 1. С помощью программы сгенерировать матрицу A и вектор b

n1=input('Номер группы:');

n2=input('Номер в списке группы:');

n=n1+n2;

rand('seed',n);

A=rand(7);

b=10*rand(7,1);

Au=triu(A);

Al=tril(A);

Ad=diag(diag(A));

su=sum(sum(abs(Au)));

sl=sum(sum(abs(Al)));

Su=sum(abs(Au));

Sl=sum(abs(Al));

sigma=5;

O=ones(7);

Ou=triu(O);

S6=diag(sigma*(Su./Sl));

At=sigma*((Al+Ou)./(Au'+Ou));

neo=rem(n2,2);

mode=rem(n2,3);

if (mode==0) Al=(sigma*su/sl)*Al; end

if (mode==1) Al=S6*Al; end

if (mode==2) Al=At.*Al; end

A=Al+Ad+Au;

ma=max(max(abs(A)));

if (ma>1000) A=0.08*A; end

A=0.5*A+2.75*diag(diag(A)); b;

% Задача 2. Проверить условия сходимости итерационных методов для матрицы A.

% Матрица А должна быть диагонально преобладающей, что значит, что ее диагональные элементы должны быть больше суммы остальных элементов строки

% При необходимости преобразовать матрицу A к виду, позволяющему вычислить решения.

for i1=1:7

S=0;

for j1=1:7

S=S+abs(A(i1,j1));

end

A(i1,i1)=S;

end

% Вывод преобразованной матрицы

A

b

% Задача 3-5. Вычислить решения с помощью метода простой итерации и Зейделя,

% количество итерации n = 20. Построить графики зависимости xi от n.

% Вычислить вектор невязки решения и ее норму. Получить точное решение СЛАУ,

% вычислить вектор погрешности решений по методам простой итерации Зейделя и их нормы.

% Оценить относительную погрешность решения СЛАУ, если ?A определяется

% десятипроцентным увеличением диагональных элементов, а ?b таким же уменьшением всех

% элементов.

% Простая итерация

% Найдем обратную матрицу к матрице диагональных элементов А

D = diag(diag(A))

T = A - D

D_inv=inv(D)

% Найдем элементы B по формуле x = Bx + g

B = -D_inv * T

g = D_inv * b

% Найдем вектор начальных приближений

x0_iteratsii = zeros(7,1)

% Постоим матрицу для графика

x_plot_iteratsii = zeros(7,1)

for i1=1:20

% Находим новые приближения по формуле метода

x0_iteratsii = B * x0_iteratsii + g

% Добавляем новые значения в график

x_plot_iteratsii = [x_plot_iteratsii x0_iteratsii]

end

% Ось для графика

n=0:20

% График для метода простых итераций

figure(1)

plot(n,x_plot_iteratsii)

% Итоговый вектор

x_pr_iteratsii = x0_iteratsii

% Невязка решения

nevazka_pr_iteratsii = A * x_pr_iteratsii - b

% Норма невязки

norm_nevazki_pr_iteratsii = norm(nevazka_pr_iteratsii)

% Получим точное решение методом Гауса

x_t_gaussa = A \ b

% Найдем погрешность решения

pogreshnost_pr_iteratsii = x_pr_iteratsii - x_t_gaussa

% Норма погрешности

norm_pogreshnosti_pr_iteratsii = norm(pogreshnost_pr_iteratsii)

% Метод Зейделя для решения СЛАУ

% Отделяем треугольные части матрицы метода итераций

B_l = tril(B)

B_u = triu(B)

% Единична матрица размера 7

E = eye(7)

% Обратная к разности матрицу

G = inv(E - B_l)

% По формуле x^(k+1)=B_l*x^(k+1)+B_u*x^(k)+c, в которой с=h, F=B_l*x+B_u

F_zeydel = G * B_u

h=G*g

% Добавим вектор начальных приближений

x0_zeydel = zeros(7,1)

% Добавим матрицу значений, переносимых на график

x_plot_zeydel = zeros(7,1)

for i2=1:20

% Заполняем вектор значений по формуле метода для новых приближений

x0_zeydel = F_zeydel * x0_zeydel + h

% Заносим точки приближения на график

x_plot_zeydel = [x_plot_zeydel x0_zeydel]

end

% Иторой график для метода зейделя

figure(2)

plot(n,x_plot_zeydel)

% Итоговый вектор после решения

x_zeydel = x0_zeydel

% Невязка метода

nevazka_zeydel = A * x_zeydel - b

% Норма невязки

norm_nevazki_zeydel = norm(nevazka_zeydel)

% Погрешность

pogreshnost_zeydel=x_zeydel-x_t_gaussa

% Норма погрешности

norm_pogreshnosti_zeydel = norm(pogreshnost_zeydel)

Графики (1 – простые итерации, 2 – метод Зейделя)

Начальная матрица

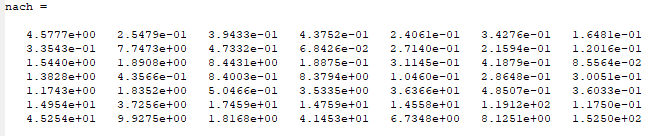
Метод итерации

Метод Зейделя