Литература и лекции / МатАнализ20171220

Тогда 1=g(x) бесконечно малая в точке a :

Без доказательства.

Теорема о произведении бесконечно малой на ограниченную

Пусть f(x) бесконечно малая в точке a ; è g(x) ограничена в некоторой окрестности точки a :

Тогда f(x) ¢ g(x) бесконечно малая в точке a :

Доказательство Зададим " > 0.

Функция f(x) бесконечно малая в точке a, следовательно, 8"1 > 0 существует

±1 = ±1("1) > 0 такое, что из неравенства jx ¡ aj < ±1("1) вытекает jf(x)j < "1. Функция g(x) ограничена в некоторой окрестности точки a, следовательно,

9 M > 0, 9 ±2 > 0, такие, что из неравенства jx ¡ aj < ±2 вытекает jg(x)j < M.

Пусть	"1 = "=M, и пусть ±(") = min (±1("=M); ±2). Тогда, из неравенства
jx ¡ aj < ±(")	вытекает справедливость неравенств jx ¡ aj < ±1("=M), jx ¡ aj < ±2,
а значит, и справедливость неравенства
	jf(x) ¢ g(x) ¡ 0j = jf(x)j ¢ jg(x)j < ("=M) ¢ M = " ;
что, по определению, и означает
	lim (f(x)			¢	g(x)) = 0 :
	x	!	a

Доказательство закончено.

Теорема о двух полицейских (для функций)

Пусть даны три числовые функции f : X ! Y ; g : X ! Y ; h : X ! Y ; значения которых 8x 2 X связаны соотношениями f(x) · g(x) · h(x) :

Пусть существуют и конечны пределы lim f(x) = lim h(x) = A :

x!a x!a

Тогда существует и конечен предел lim g(x) ; ïðè÷¼ì, lim g(x) = A :

x!a x!a

21

4. lim

Без доказательства.

Замечание Теорема сохраняет силу, если все обычные пределы в ней заменены правосто-

ронними, или если все обычные пределы в ней заменены левосторонними.

Теорема	об арифметических действиях над пределами функций
	Пусть существуют и конечны пределы lim f(x) = A è	lim g(x) = B :
	x!a	x!a
Тогда

1.

2.

3.

lim(f(x) + g(x)) = lim f(x) + lim g(x) = A + B :

x!a x!a x!a

lim(f(x)

¡

g(x)) = lim f(x)

lim g(x) = A

¡

B :

x

!

a

x

!

a

¡ x

!

a

lim(f(x)

¢

g(x)) = lim f(x)

lim g(x) = A

¢

B :

x

!

a

x

!

a

¢x a

!

f(x)

lim f(x)

A

=

x!a

=

:

x!a g(x)

lim g(x)

B

x!a

Доказательство приводится только для Пункта 3 1. Случай 1: A > 0 ; B > 0 :

Зададим " > 0 .

Не умаляя общности, поставим ограничение

" < AB :

(28)

Выпишем целевое неравенство

jf(x) ¢ g(x) ¡ ABj < " () ¡" < f(x) ¢ g(x) ¡ AB < +" :

(29)

По условию lim f(x) = A ; а это значит, что "		0	>	0	существует ±	("	) > 0
x a	8				1	0
!	следует jf(x) ¡ Aj < "0 ;
такое, что из jx ¡ aj < ±1("0)		а это неравенство с модулем
равносильно двойному неравенству
	A ¡ "0 < f(x) < A + "0 :						(30)

22

По условию lim g(x) = B ; а это значит, что "			0	> 0 существует ±		("	) > 0
x a		8			2	0
!
такое, что из jx ¡ aj < ±2("0) следует jg(x) ¡ Bj < "0 ;			а это неравенство с модулем
равносильно двойному неравенству
B ¡ "0 < g(x) < B + "0 :							(31)
Поставим два дополнительных ограничения:
A ¡ "0 > 0	()	"0 < A ;					(32)
B ¡ "0 > 0	()	"0 < B ;					(33)
Позже будет показано, что выполнение требований (32) (33) ïðè					A > 0 ; B > 0
автоматически следует из (28).

 ñèëó (32) (33), все три части неравенства (30) и все три части неравенства (31)

положительны, следовательно, эти два неравенства можно друг на друга умножить, в результате чего будет справедливо неравенство

(A ¡ "0)(B ¡ "0) < f(x)g(x) < (A + "0)(B + "0) ()

() AB ¡ (A + B)"0 + "20 < f(x)g(x) < AB + (A + B)"0 + "20 () ¡(A + B)"0 + "20 < f(x)g(x) ¡ AB < (A + B)"0 + "20 :

Пусть ±("0) = min (±1("0); ±2("0)). Тогда при jx ¡ aj < ±("0) неравенства (30), (31), следовательно, выполняется и (34).

	Пусть	2 "
	"0 =				:
			A + B + p
				(A + B)2 + 4 "

()

(34)

справедливы

(35)

Непосредственной подстановкой можно убедиться в том, что

(A + B)"0 + "02 = " :

(36)

Собственно, представление (35) найдено решением квадратного уравнения (36) îòíî-

сительно "0 :

Кроме того, нетрудно доказать неравенство

¡(A + B)"0 + "02 > ¡" :

(37)

23

Тогда при

jx ¡ aj < ±("0) = ±ÃA + B +

(A + B)2 + 4 "!

выполняется неравенство

2 "

2

p

2

= +" =)

¡" < ¡(A + B)"0 + "0

< f(x) ¢ g(x) ¡ AB < (A + B)"0 + "0

|

{z

}

" < f(x)

g(x) AB|

{z

}

(38)

=

< +" :

(37)

(36)

)

¡

¢

¡

то есть, на этом доказательство для случая A > 0 ; B > 0

закончено.

Осталось "раздать" немногочисленные долги. Слушателю, претендующему на оценку не выше, чем "Хорошо", читать оставшуюся часть доказательства Случая 1 необязательно.

Докажем неравенство (37):

¡(A + B)"0 + "20 > ¡" () ¡(A + B)"0 + "20 + " > 0 ()

8"2

() ³ p ´2 > 0 : (39) A + B + (A + B)2 + 4"

Справедливость последнего из неравенств не вызывает сомнений, поскольку числитель и знаменатель в левой части (39) строго положительны.

Докажем неравенство (32):

A + B + (A + B)2		+ 4 " < A () 2 " < A ¢ ³A + B + p(A + B)2					+ 4 "´		()
	2 "
p	() 2 " ¡ A2 ¡ AB < A ¢ p					:
				(A + B)2 + 4 "					(40)

Если левая часть в (40) строго меньше нуля, то справедливость неравенства

очевидна (поскольку правая часть строго положительна) следовательно, и справедливость (32) доказана.

Если левая часть в (40) неотрицательна, цепь равносильных преобразований должна быть продолжена:

() 2 " ¡ A2 ¡2 AB < A ¢	p		()2
		(A + B)2 + 4 "
				()
() ¡2 " ¡ A2 ¡ AB¢ < A2 ¢ ³pA2 + 2AB + B2 + 4 "´

24

() 4 "2 + A4 + A2B2 ¡ 4 "A2 ¡ 4 "AB + 2A3B < A4 + 2A3B + A2B2 + 4A2" ()

() 4 "2 + ¡4 "A2 ¡ 4 "AB < +4A2"				()
() 4 "2 < 8A2" + 4 "AB		()	"2 < 2A2" + "AB ()
()		" < 2A2 + AB :			(41)
Таким образом, осталось доказать (41). Согласно договор¼нности (28)
" < AB ; AB < AB + 2A2			=) " < AB + 2A2 :
Неравенство (32) доказано.		|{z}		(33)
		>0
	Доказательство неравенства				строится аналогич-

íî.

2. Случай 2: A < 0 ; B < 0 :

Воспользуемся двумя вспомогательными функциями f1(x) = ¡f(x), g1(x) = ¡g(x). Тогда

lim f

(x) = (

¡

A) > 0 ;

lim g

(x) = (

B) > 0 :

x a 1

x

!

a 1

¡

!

В соответствии со Случаем 1,

lim f(x)

¢

g(x) = lim ((

f (x))

¢

(

g (x))) = lim (f

(x)

¢

g

(x)) = (

¡

A)( B) = AB :

x a

x a

¡ 1

¡ 1

x a

1

1

¡

!

!

!

3. Случаи A < 0 ; B > 0 è A > 0 ; B < 0

предлагается изучить самостоятельно.

Теорема

о замене переменной под знаком предела для функций

Пусть существуют и конечны пределы

lim f(y) = A è

lim g(x) = B :

y!B

x!a

Тогда существует и конечен предел

lim f(g(x)) = A :

Доказательство

x!a

lim f(y) = A ; следовательно, " > 0

9

±

1

= ±

(") > 0 такое, что из неравенства

y

!

B

8

1

jy ¡ Bj < ±1(") следует справедливость неравенства jf(y) ¡ Aj < " .

25

lim g(x) = B ; следовательно, "

2

>

0

(если для любого "

2

; òî è äëÿ "

2

=

±

"

)

x a

8

1( )

!

такое, что из неравенства

jx ¡ aj < ±2("2) = ±2(±1("1))

9 ±2 = ±2("2) = ±2(±1("1)) > 0

следует справедливость неравенства jg(x) ¡ Bj < "2 = ±1(") .

Итак, при любом заданном " > 0 существует такое значение функции ±2(±1(")) ;

благодаря которому справедлива цепь следований

jx ¡ aj < ±2(±1(")) =) j g(x) ¡Bj < ±1(") =) jf(g(x)) ¡ Aj < " ;

что, по определнию предела,

|{z}lim f(g(x)) = A .

|{z}

=y

=y

означает

x!a

Определение непрерывности функции в точке

Если функция f : X ! Y имеет в конечной точке a 2 X конечный предел

lim f(x) ,

x!a

èсуществует конечное значение функции f(a) в этой точке,

èïðè ýòîì lim f(x) = f(a) ,

x!a

òî принято говорить, что функция f(x) непрерывна в точке a.

Замечание Иногда удобнее пользоваться вторым, равноценным первому определением непре-

рывности функции в точке. Если существует конечное значение f(x) ; è

lim (f(x + x) ¡ f(x)) = 0 ;

x!0

то функция непрерывна в точке x.

Определение непрерывности функции на множестве

Если функция f : X ! Y непрерывна 8x 2 X,

òî принято говорить, что функция f непрерывна на множестве X.

Теорема о непрерывности элементарных функций Все элементарные функции непрерывны на всей области своего залания.

26

Непрерывны также комбинации элементарных функций, построенные с помощью обычных арифметических операций.

К элементарным функциям относятся:

степенная функция с любым действительным показателем,

показательная функция,

логарифмическая функция,

тригонометрические функции,

обратные тригонометрические функции.

Без доказательства.

Классификация			разрывов функции
1.		Если существует и конечен предел lim f(x) = A , íî							f(a) = A , ëèáî
							x	a	6
							!
	f(a)		не существует, то принято говорить, что функция f(x) имеет в точке
	x = a устранимый разрыв.
2.		Если существуют и конечны односторонние пределы							lim f(x) = A ;
									x!a+0
	lim		f(x) = B ; íî A = B , то принято говорить, что функция f(x) имеет
	x a	¡	0	6
!
	в точке x = a разрыв 1 го рода.
2.		Если не существует или бесконечен хотя бы один из односторонних
	пределов lim f(x) ,			lim f(x) , то принято говорить, что функция f(x)
			x!a+0	x!a¡0
	имеет в точке x = a разрыв 2 го рода.
Пример
Несколько позже будет доказано, что						lim	sin x	= 1. Значение функции f(x) =
						x!0	x
sin x
x не существует при x = 0 : Это означает, что функция f(x) терпит устранимый
разрыв в точке			x = 0 . "Устранить" разрыв можно, если определить искусственную
функцию					sinxx;	x 6= 0		¯ :
			˜
			f(x) = ½		1;	x = 0
								¯
								¯
								¯

27

Пример В математике применяется стандартная функция "Сигнум", определяемая так:

sign x =

8

¡1;

x < 0

¯

:

+1;

x > 0

>

¯

<

0;

x = 0

¯

¯

>

¯

¯

Очевидно, что

¡

:,

lim sign x =¯

, следовательно, функция

lim sign x =

1

+1

x

!¡

0

x +0

!

терпит в точке

x = 0 разрыв первого рода.

Пример

В школьной математике изучалась функция

f(x) = 1=x.

Очевидно, что

f

(

x

) = ¡1

, lim f(x) = +

, следовательно, функция терпит в

xlim0

x +0

1

!¡

!

точке x = 0 разрыв второго рода.

Теорема о промежуточных значениях функции (теорема Коши) Пусть функция f(x) непрерывна на промежутке [a; b] .

Åñëè f(a) < f(b) , òî 8 C 2 [f(a); f(b)] 9 c 2 [a; b] такое, что f(c) = C . Åñëè f(a) > f(b) , òî 8 C 2 [f(b); f(a)] 9 c 2 [a; b] такое, что f(c) = C .

Без доказательства.

Следствие о существовании корня функции на промежутке

Пусть функция f(x) непрерывна на промежутке [a; b] ;

и пусть f(a) ¢ f(b) < 0 (значения функции на концах промежутка имеют

противоположные знаки).

Тогда 9 c 2 (a; b) такое, что f(c) = 0.

Теорема о первом замечательном пределе

lim sin x = 1 :

x!0 x

28

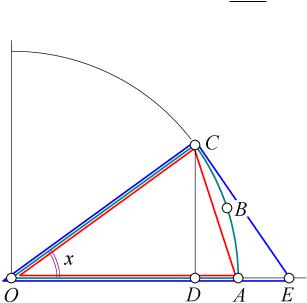
Доказательство Сначала найд¼м правосторонний предел

lim sin x :

x!+0 x

Ðèñ. 1

Будем считать, что 0 < x < ¼=2, и у круга радиуса R нас интересует только первая его четверть. Отмеряем угол x от горизонтальной оси против часовой стрелки

(Рис. 1) Единица измерения углов радиан.

Обозначим следующие точки: O центр окружности, A пересечение окружности с горизонтальной осью, C точка на окружности, соответствующая углу x, B точка на окружности, расположенная между A è C, D основание перпендикуляра, опущенного из точки C на отрезок OA, E точка пересечения касательной к окружности (в точке касания C) с горизонтальной осью. CE ? OC, так как касательная

перпендикулярна радиусу, провед¼нному в точку касания.

Рассмотрим три фигуры: треугольник OAC, сектор OABC, и треугольник OCE. Найд¼м площади этих фигур:

S OAC = 12 ¢ OA ¢ CD = 12 ¢ R ¢ R sin x = 12 ¢ R2 sin x,

SOABC = 12 ¢ R2 ¢ x,

S OCE = 12 ¢ OC ¢ CE = 12 ¢ R ¢ R tan x = 12 ¢ R2 tan x.

Очевидно, что OAC ½ OABC ½ OCE, значит, S OAC < SOABC < S OCE,

29

что равносильно неравенствам

1

<

1

<

1

()

2

<

2

<

2

()

S OCE

SOABC

S OAC

R2 tan x

R2x

R2 sin x

()

1

1

1

()

sin x

sin x

sin x

() cos x <

sin x

<

<

<

<

< 1 : (42)

tan x

x

sin x

tan x

x

sin x

x

Справедливость последнего неравенства в (42), а также равенств lim cos x = 1

x!0

(в силу непрерывности функции cos x),

lim 1 = 1, да¼т право применить теорему о

двух полицейских, следовательно,

x!0

lim

sin x

= 1 :

x

x!+0

Теперь найд¼м левосторонний предел

lim

sin y

=

y = ¡x; x = ¡y

¸

= lim

sin(¡x)

= lim

¡ sin x

=

lim

sin x

= 1 :

¡x

y!¡0

y

·

x ! +0

x!+0

¡x

x!+0

x!+0

x

Поскольку оба односторонних предела существуют и равны единице, по Теореме о связи предела с односторонними пределами мы вправе утверждать, что

lim sin x = 1 :

x!0 x

Доказательство закончено.

Теорема о втором замечательном пределе

x

x

x

µ

1

¶

µ

1

¶

µ

1

¶

1

lim

1 +

= lim

1 +

= lim

1 +

lim (1 + y)y

= e :

x

x

x

x!+1

x!¡1

x!1

= y!0

Доказательство строится на основе доказательства для второго замечательного предела последовательности, ничего увлекательного не содержит и здесь не приводится.

Теорема о третьем замечательном пределе

lim ln(1 + x) = 1 :

x!0 x

Доказательство

	lim	ln(1 + x)		= lim ln(1 + x)1=x = ln lim(1 + x)1=x = ln e = 1 :
		x
	x!0			x!0	x!0

30