
- •Т. Н. Матыцина е. К. Коржевина линейная алгебра
- •Оглавление
- •Введение
- •1. Множества
- •1.1. Множества и их элементы. Способы задания множеств
- •1.2. Подмножества. Диаграммы Эйлера – Венна
- •1.3. Операции над множествами и их свойства
- •1. Объединение (или сумма).
- •2. Пересечение (или произведение).
- •3. Разность.
- •4. Декартовое произведение (или прямое произведение).
- •Свойства операций над множествами
- •1.4. Метод математической индукции
- •1.5. Комплексные числа
- •Операции над комплексными числами
- •Геометрическая интерпретация комплексных чисел
- •Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме
- •3. Возведение в степень.
- •4. Извлечение корня n-ой степени.
- •Показательная форма комплексного числа
- •2. Бинарные отношения
- •2.1. Понятие отношения
- •Способы задания бинарных отношений
- •Операции над бинарными отношениями
- •2.2. Свойства бинарных отношений
- •2.3. Отношение эквивалентности
- •2.4. Функции
- •3. Матрицы и действия над ними
- •3.1. Общие понятия
- •3.2. Основные операции над матрицами и их свойства
- •3.2.1. Сложение однотипных матриц
- •3.2.2. Умножение матрицы на число
- •3.2.3. Умножение матриц
- •3.3. Транспонирование матриц
- •4. Определители квадратных матриц
- •4.1. Определители матриц второго и третьего порядка
- •4.2. Определитель матрицы n-го порядка
- •4.3. Свойства определителей
- •4.4. Практическое вычисление определителей
- •5. Ранг матрицы. Обратная матрица
- •5.1. Понятие ранга матрицы
- •5.2. Нахождение ранга матрицы методом окаймления миноров
- •5.3. Нахождение ранга матрицы с помощью элементарных преобразований
- •5.4. Понятие обратной матрицы и способы ее нахождения
- •Алгоритм нахождения обратной матрицы
- •Нахождение обратной матрицы с помощью элементарных преобразований
- •6. Системы линейных уравнений
- •6.1. Основные понятия и определения
- •6.2. Методы решения систем линейных уравнений
- •6.2.1. Метод Крамера
- •6.2.2. Метод обратной матрицы
- •6.2.3. Метод Гаусса
- •Описание метода Гаусса
- •6.3. Исследование системы линейных уравнений
- •6.4. Однородные системы линейных уравнений
- •Свойства решений однородной системы линейных уравнений
- •Фундаментальный набор решений однородной системы линейных уравнений
- •7. Арифметическое n-мерное векторное пространство
- •7.1. Основные понятия
- •7.2. Линейная зависимость и независимость системы векторов
- •Свойства линейной зависимости системы векторов
- •Единичная система векторов
- •Две теоремы о линейной зависимости
- •7.3. Базис и ранг системы векторов
- •Базис пространства Rn
- •Ранг системы векторов
- •8. Векторные (линейные) пространства
- •8.1. Определение векторного пространства над произвольным полем.
- •Простейшие свойства векторных пространств
- •Линейная зависимость и независимость системы векторов
- •8.2. Подпространства. Линейные многообразия
- •Пересечение и сумма подпространств
- •Линейные многообразия
- •8.3. Базис и размерность векторного пространства
- •8.3.1. Конечномерные векторные пространства
- •Базис конечномерного векторного пространства
- •8.3.2. Базисы и размерности подпространств
- •8.3.3. Координаты вектора относительно данного базиса
- •8.3.4. Координаты вектора в различных базисах
- •8.4 Евклидовы векторные пространства
- •Скалярное произведение в координатах
- •Метрические понятия
- •Процесс ортогонализации
- •Скалярное произведение в ортонормированном базисе
- •Ортогональное дополнение подпространства
- •9. Линейные операторы
- •9.1. Основные понятия и способы задания линейных операторов
- •Способы задания линейных операторов
- •9.2. Матрица линейного оператора Связь между координатами вектора и координатами его образа
- •Матрицы линейного оператора в различных базисах
- •9.3. Подобные матрицы
- •Свойства отношения подобия матриц
- •9.4. Действия над линейными операторами
- •1. Сложение линейных операторов.
- •Свойства сложения линейных операторов
- •9.5. Ядро и образ линейного оператора
- •9.6. Обратимые линейные операторы
- •9.7. Собственные векторы линейного оператора
- •9.7.1. Свойства собственных векторов
- •9.7.2. Характеристический многочлен матрицы
- •9.7.3. Нахождение собственных векторов линейного оператора
- •9.7.4. Алгоритм нахождения собственных векторов линейного оператора
- •9.7.5.Условия, при которых матрица подобна диагональной матрице
- •10. Жорданова нормальная форма матрицы линейного оператора
- •10.1. Понятие λ-матрицы
- •Свойства λ-матрицы
- •10.2. Жорданова нормальная форма
- •10.3.Приведение матрицы к жордановой (нормальной) форме
- •Алгоритм приведения матрицы a к жордановой форме
- •11. Билинейные и квадратичные формы
- •11.1. Билинейные формы
- •Свойства билинейных форм
- •Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы
- •11.2. Квадратичные формы
- •Приведение квадратичной формы к каноническому виду
- •Закон инерции квадратичных форм
- •Классификация квадратичных форм
- •Необходимое и достаточное условие знакоопределенности квадратичной формы
- •Необходимое и достаточное условие знакопеременности квадратичной формы
- •Необходимое и достаточное условие квазизнакопеременности квадратичной формы
- •Критерий Сильвестра знакоопределенности квадратичной формы
- •Заключение
- •Библиографический список
- •Линейная алгебра
- •156961, Г. Кострома, ул. 1 Мая, 14
3.3. Транспонирование матриц
Определение 3.16. Матрица Аt, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной матрице А.
Если A – матрица размерности m n, то Аt – матрица размерности n m.
При транспонировании верны следующие равенства:
(А + В)t = Аt + Вt;
(kA)t = kАt;
(AB)t = ВtАt.
4. Определители квадратных матриц
4.1. Определители матриц второго и третьего порядка
Каждой
квадратной матрице А
порядка n
ставится в соответствие число, которое
называется определителем
этой матрицы. Обозначение: ,
|A|,
det A,
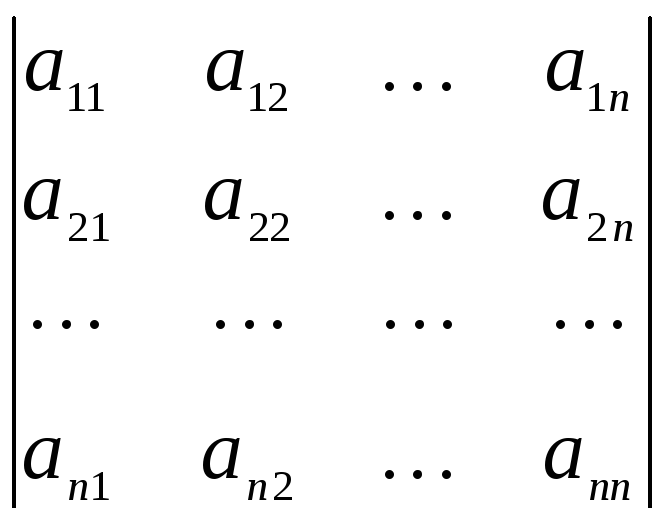 .
.
Определение 4.1. Определителем матрицы первого порядка А = (а11) называется число а11.
Пример 4.1. Например: если дана матрица первого порядка А = (3), то определитель этой матрицы |A| = 3.
Определение 4.2.
Определителем
матрицы второго порядка
А =  называется число, которой находится по
формуле: |A| =
называется число, которой находится по
формуле: |A| = ![]() = а11а22 – а12а21.
= а11а22 – а12а21.
Пример 4.2.
Если
дана матрица второго порядка А = ![]() ,
то определитель этой матрицы
|A| =
,
то определитель этой матрицы
|A| = ![]() = 14 – 23 = 4 – 6 = –2.
= 14 – 23 = 4 – 6 = –2.
Определение 4.3.
Определителем
матрицы третьего порядка
А = 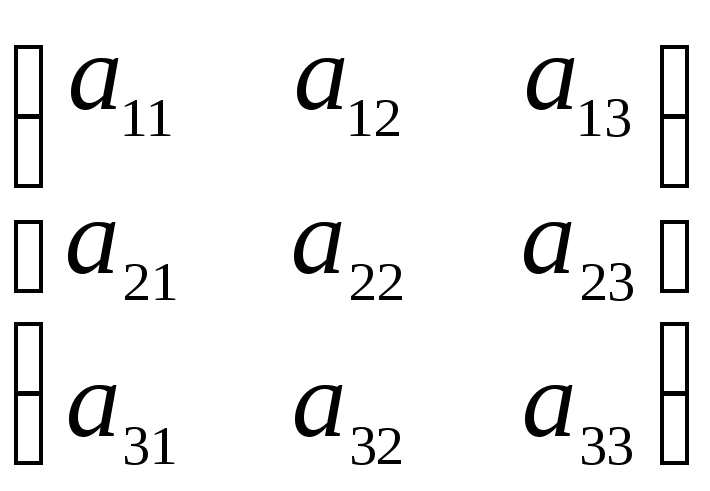 называется число, которой находится по
формуле:
|A| = а11а22а33 + а12а31а23 + а21а13а32 – а13а22а31 – а11а32а23 – а33а21а12.
называется число, которой находится по
формуле:
|A| = а11а22а33 + а12а31а23 + а21а13а32 – а13а22а31 – а11а32а23 – а33а21а12.
Это число состоит из шести слагаемых, в каждое слагаемое в качестве множителей входит по одному элементу из каждой строки и каждого столбца. Для запоминания формулы можно воспользоваться наглядным правилом знаков для выписывания произведений, входящих в разложение определителя третьего порядка. Схема на рис. 4.1 называется правилом треугольника или правилом Саррюса10.
Правило составления выражения для определителя третьего порядка строится следующим образом. Из членов, входящих со знаком «+», один будет произведением элементов главной диагонали, каждый из двух других – произведением элементов, лежащих на параллели к этой диагонали, с добавлением третьего множителя из противоположного угла матрицы (рис. 4.1). Члены, входящие со знаком «–», строятся таким же, образом относительно другой диагонали.
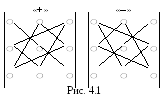
Существует еще вторая схема правила Саррюса: к определителю приписывают справа два первых столбца и вычисляют сумму произведений элементов расположенных на главной диагонали и «прямых», параллельных ей, со знаком минус вычисляют сумму произведений элементов, расположенных на побочной диагонали, и «прямых», параллельных ей.
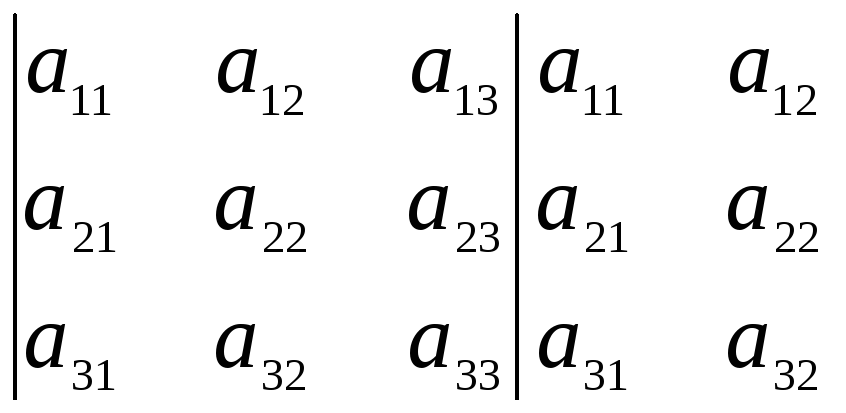 = а11а22а33 + а12а23а31 + а13а21а32 – а13а22а31 – а11а23а32 – а12а21а33.
= а11а22а33 + а12а23а31 + а13а21а32 – а13а22а31 – а11а23а32 – а12а21а33.
Пример 4.3.
Если дана матрица третьего порядка
А =  ,
то определитель этой матрицы
|A| =
,
то определитель этой матрицы
|A| = 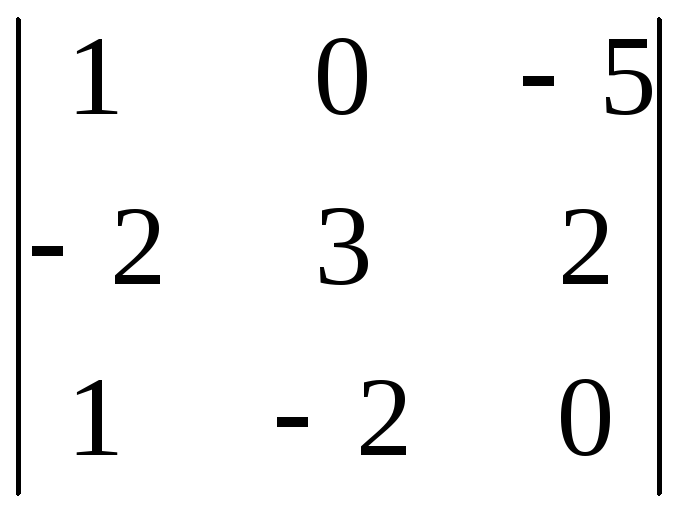 = 130 + 102 + (–5)(–2)(–2) – (–5)31 – 12(–2) –
– 00(–2) = –20 + 15 + 4 = –1.
= 130 + 102 + (–5)(–2)(–2) – (–5)31 – 12(–2) –
– 00(–2) = –20 + 15 + 4 = –1.
4.2. Определитель матрицы n-го порядка
Для того чтобы дать определение определителя произвольного порядка, введем некоторые понятия. Пусть аij – элемент определителя порядка n, где i, j = 1, 2, …, n.
Определение 4.4. Минором элемента аij называется определитель Mij, полученный из данного определителя вычеркиванием i-ой строки и j-го столбца.
Из определения следует, что минор элемента – это определитель (n – 1) порядка.
Определение 4.5. Алгебраическим дополнением элемента аij называется его минор, взятый со знаком (–1)i + j, т. е. Аij = (–1)i + jMij.
Для определения понятия определителя n-го порядка воспользуемся индукцией по n, где n – порядок матрицы A.
Определение 4.6.
1. При n = 1 матрица А состоит из одного числа: |A| = а11.
2. Пусть для матрицы порядка (n – 1) определитель известен.
3. Определителем
матрицы А
произвольного порядка n
называется число, находящееся по формуле:
|A| = ![]() ,
где суммирование распространяется на
все элементы матрицы А.
,
где суммирование распространяется на
все элементы матрицы А.
Эта формула сводит вычисление определителей порядка n к вычислению определителей порядка (n – 1).
