11. Билинейные и квадратичные формы

11.1. Билинейные формы

Определение 11.1. Билинейной формой называется функция (отображение) f: V  V  R (или C), где V – произвольное векторное пространство, и для любых векторов x, y  V и любого числа λ  R (или C) выполняются соотношения

f(x + y, z) = f(x, y) + f(z, y),

f(x, y + z) = f(x, y) + f(x, z),

f(λx, y) = λf(x, y),

f(x, λy) = λf(x, y).

Обозначим число, получаемое в результате отображения пары векторов x и y, как A(x, y) .

Определение 11.2. Билинейная форма A(x, y) называется симметрической, если для любых x, y  V выполняется: A(x, y) = A(y, x).

Определение 11.3. Билинейная форма A(x, y) называется кососимметрической, если для любых x, y  V выполняется: A(x, y) = –A(y, x).

Свойства билинейных форм

Любую билинейную форму можно представить в виде суммы симметричной кососимметричной форм.

При выбранном базисе e₁, e₂, …, e_n в векторном пространстве V любая билинейная форма A однозначно определяется матрицей

A(е) = ,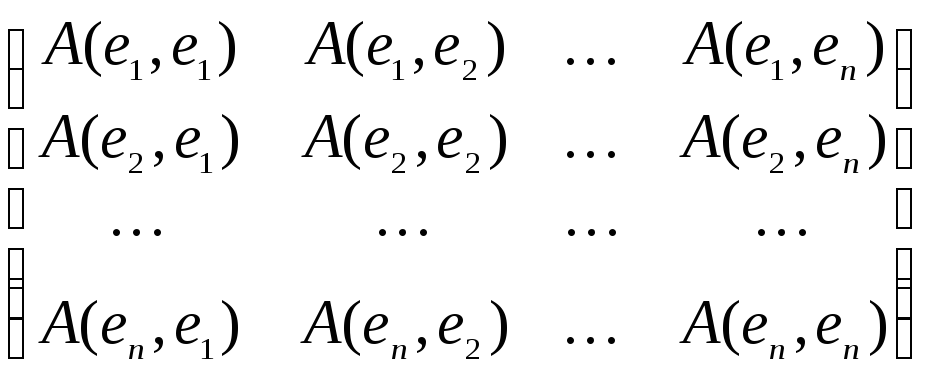

так, что для любых x = x₁e₁ + x₂e₂ + … + x_ne_n, y = y₁e₁ + y₂e₂ + … + y_ne_n;

A(x, y) = (x₁ x₂ … x_n), то есть

A(x, y) = ,где А_ij = A(e_i, e_j). (1)

Вид (1) назовем общим видом билинейной формы в n-мерном векторном пространстве.

Замечание. Если билинейная форма A(x, y) симметрическая, то и матрица (A_ij) будет симметрической, то есть A_ij = A_ji для i, j = 1, 2, …, n. Если билинейная форма A(x, y) кососимметрическая, то и матрица (A_ij) будет кососимметрической, то есть A_ij = –A_ji для i, j = 1, 2, …, n.

Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы

Пусть в векторном пространстве V заданы два базиса e = {e₁, e₂, …, e_n} и f = {f₁, f₂, …, f_n}. Пусть A(e) = (а_ij) и A(f) = (b_ij) – матрицы билинейной формы A в указанных базисах.

Теорема 11.1. Матрицы A(e) и A(f) билинейной формы A(x, y) в базисах {e} и {f} связаны соотношением

A(f) = C^tA(e)C, (),

где C – матрица перехода от базиса {e} к базису {f}, а C^t –транспонированная матрица C.

Следствие. Ранг матрицы A(f) равен рангу матрицы A(e).

Это утверждение следует из равенства (): так как С – матрица перехода от одного базиса к другому, то матрица С и матрица C^t– невырожденные, поэтому умножение на них матрицы A(e) не меняет ее ранга.

Определение 11.4. Рангом билинейной формы, заданной в конечномерном векторном пространстве V , называется ранг матрицы этой формы в произвольном базисе пространства V.

Определение 11.5. Билинейная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

11.2. Квадратичные формы

Пусть A(x, y) – симметрическая билинейная форма, заданная на векторном пространстве V.

Определение 11.6. Квадратичной формой называется числовая функция одного векторного аргумента x, которая получается из билинейной формы A(x, y) при x = y.

Определение 11.7. Симметрическая билинейная форма A(x, y) называется полярной квадратичной форме A(x, x).

Пусть дана билинейная форма A(x, y) = , положим в ней x_i = y_j, тогда мы получим представление квадратичной формы A(x, x) в конечномерном векторном пространстве V с заданным базисом {e}:

A(x, x) = . (2)

Определение 11.8. Матрица (a_ij) называется матрицей квадратичной формы A(x, x) в заданном базисе {e}.

При переходе к новому базису матрица квадратичной формы преобразуется по формуле A(f) = C^tA(e)C и ранг этой матрицы не меняется при переходе к новому базису.

Определение 11.9. Ранг матрицы квадратичной формы A(x, x) называется рангом квадратичной формы.

Определение 11.10. Квадратичная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

Определение 11.11. Квадратичная форма A(x, x) называется

1. Положительно определенной, если для любого ненулевого вектора x выполняется неравенство A(x, x) > 0.

2. Отрицательно определенной, если для любого ненулевого вектора x выполняется неравенство A(x, x) < 0.

3. Знакопеременной, если существуют такие x и y, что A(x, x) > 0 и A(y, y) < 0.

4. Квазизнакоопределенной, если для всех x, A(x, x) ≥ 0 (или A(x, x) ≤ 0) и имеется вектор x ≠ 0, для которого A(x, x) = 0.

Замечание. Если A(x, y) – билинейная форма, полярная положительно определенной квадратичной форме A(x, x), то A(x, y) удовлетворяет аксиомам скалярного произведения векторов в евклидовом пространстве:

1. A(x, y) = A(y, x) – в силу симметричности A(x, x).

2. A(x + y, z) = A(x, z) + A(y, z) – в силу определения билинейной формы.

3. A(λx, y) = λA(x, y) – в силу определения билинейной формы.

4. A(x, x) ≥ 0 и A(x, x) > 0 при х ≠ 0, т. к. A(x, x) положительно определена.

Вывод. Скалярное произведение в векторных пространствах может быть задано с помощью билинейной формы:

(x, y) =  = A(x, y).