Приведение квадратичной формы к каноническому виду
Дана
квадратичная форма (2) A(x, x) = 
,
где x = (x1, x2, …, xn).
Рассмотрим квадратичную форму в
пространстве R3,
то есть x = (x1,
x2,
x3),
A(x,
x) = 
+ 
+ 
+ 
+ 
+ 
+
+ 
+ 
+ 
= 
+ 
+ 
+ 2
+ 2
+
+ 2
(использовали условие симметричности
формы, а именно а12 = а21,
а13 = а31,
а23 = а32).
Выпишем матрицу квадратичной формы A
в базисе {e},
A(e) =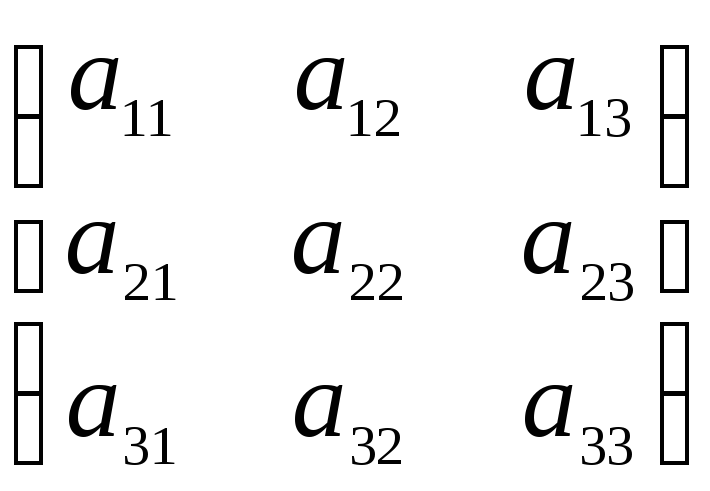 
.
При изменении базиса матрица квадратичной
формы меняется по формуле A(f) = CtA(e)C,
где C
– матрица перехода от базиса {e}
к базису {f},
а Ct
– транспонированная матрица C.
Определение 11.12. Вид квадратичной формы с диагональной матрицей называется каноническим.
Итак,
пусть A(f) =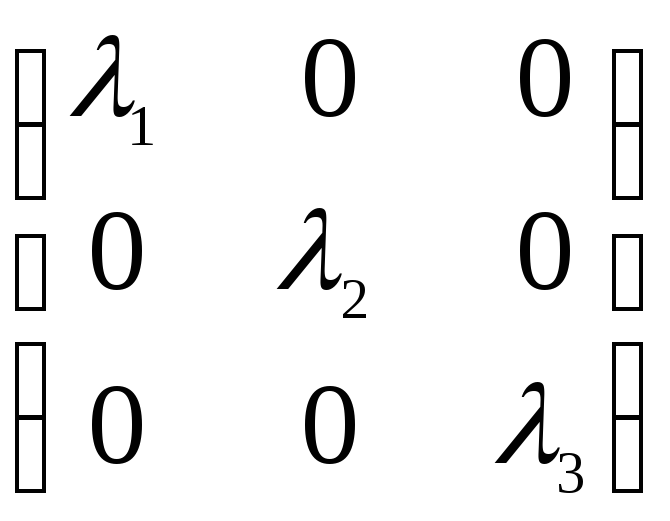 
,
тогда A'(x,
x) = 
+ 
+ 
,
где x'1,
x'2,
x'3
– координаты вектора x
в новом базисе {f}.
Определение 11.13. Пусть в n-мерном векторном пространстве V выбран такой базис f = {f1, f2, …, fn}, в котором квадратичная форма имеет вид
A(x, x) = 
+ 
+ … + 
,
(3)
где y1, y2, …, yn – координаты вектора x в базисе {f}. Выражение (3) называется каноническим видом квадратичной формы. Коэффициенты 1, λ2, …, λn называются каноническими; базис, в котором квадратичная форма имеет канонический вид, называется каноническим базисом.
Замечание. Если квадратичная форма A(x, x) приведена к каноническому виду, то, вообще говоря, не все коэффициенты i отличны от нуля. Ранг квадратичной формы равен рангу ее матрицы в любом базисе.
Пусть
ранг квадратичной формы A(x, x)
равен r,
где r ≤ n.
Матрица квадратичной формы в каноническом
виде имеет диагональный вид. A(f) = 
,
поскольку ее ранг равен r,
то среди коэффициентов i
должно быть r,
не равных нулю. Отсюда следует, что число
отличных от нуля канонических коэффициентов
равно рангу квадратичной формы.
Замечание. Линейным преобразованием координат называется переход от переменных x1, x2, …, xn к переменным y1, y2, …, yn, при котором старые переменные выражаются через новые переменные с некоторыми числовыми коэффициентами.
x1 = α11y1 + α12y2 + … + α1nyn,
x2 = α21y1 + α22y2 + … + α2nyn,
………………………………
x1 = αn1y1 + αn2y2 + … + αnnyn.
Так как каждому преобразованию базиса отвечает невырожденное линейное преобразование координат, то вопрос о приведении квадратичной формы к каноническому виду можно решать путем выбора соответствующего невырожденного преобразования координат.
Теорема 11.2 (основная теорема о квадратичных формах). Всякая квадратичная форма A(x, x), заданная в n-мерном векторном пространстве V, с помощью невырожденного линейного преобразования координат может быть приведена к каноническому виду.
Доказательство. (Метод Лагранжа) Идея этого метода состоит в последовательном дополнении квадратного трехчлена по каждой переменной до полного квадрата. Будем считать, что A(x, x) ≠ 0 и в базисе e = {e1, e2, …, en} имеет вид (2):
A(x,
x) = 
.
Если A(x, x) = 0, то (aij) = 0, то есть форма уже каноническая. Формулу A(x, x) можно преобразовать так, чтобы коэффициент a11 ≠ 0. Если a11 = 0, то коэффициент при квадрате другой переменной отличен от нуля, тогда при помощи перенумерации переменных можно добиться, чтобы a11 ≠ 0. Перенумерация переменных является невырожденным линейным преобразованием. Если же все коэффициенты при квадратах переменных равны нулю, то нужные преобразования получаются следующим образом. Пусть, например, a12 ≠ 0 (A(x, x) ≠ 0, поэтому хотя бы один коэффициент aij ≠ 0). Рассмотрим преобразование
x1 = y1 – y2,
x2 = y1 + y2,
xi = yi, при i = 3, 4, …, n.
Это
преобразование невырожденное, так как
определитель его матрицы отличен от
нуля
= 
= 2 ≠ 0.
Тогда
2a12x1x2 = 2
a12(y1 – y2)(y1 + y2) = 2
– 2
,
то есть в форме A(x,
x)
появятся квадраты сразу двух переменных.
Итак, станем считать, что в равенстве (2) a11 ≠ 0. Выделим в выражении (2) группу слагаемых, которые содержат x1. Получим:
A(x,
x) =
+ 2
+ 2
+ 
. (4)
Преобразуем
выделенную сумму к виду:
A(x,
x) = a11
, (5)
при
этом коэффициенты aij
меняются на 
.
Рассмотрим невырожденное преобразование
y1 = x1 + 
+ … + 
,
y2 = x2,
………
yn = xn.
Тогда получим
A(x,
x) = 
.
(6).
Если
квадратичная форма 
= 0,
то вопрос о приведении A(x, x)
к каноническому виду решен.
Если эта форма не равна нулю, то повторяем рассуждения, рассматривая преобразования координат y2, …, yn и не меняя при этом координату y1. Очевидно, что эти преобразования будут невырожденными. За конечное число шагов квадратичная форма A(x, x) будет приведена к каноническому виду (3).
Замечание 1. Нужное преобразование исходных координат x1, x2, …, xn можно получить путем перемножения найденных в процессе рассуждений невырожденных преобразований: [x] = A[y], [y] = B[z], [z] = C[t], тогда [x] = AB[z] = ABC[t], то есть [x] = M[t], где M = ABC.
Замечание 2.
Пусть
A(x,
x) = A(x, x) = 
+
+ …+ 
,
где i≠ 0,
i = 1,
2, …, r,
причем 1 > 0,
λ2 > 0,
…, λq > 0,
λq+1 < 0,
…, λr < 0.
Рассмотрим невырожденное преобразование
y1 = 
z1,
y2 = 
z2,
…, yq = 
zq,
yq+1 = 
zq+1,
…, yr = 
zr,
yr+1 = zr+1,
…, yn = zn.
В
результате A(x,
x)
примет вид:
A(x, x) = 
+ 
+ … + 
– 
– … – 
,
который называется нормальным
видом квадратичной формы.
Пример 11.1. Привести к каноническому виду квадратичную форму A(x, x) = 2x1x2 – 6x2x3 + 2x3x1.
Решение. Поскольку a11 = 0, используем преобразование
x1 = y1 – y2,
x2 = y1 + y2,
x3 = y3.
Это
преобразование имеет матрицу A =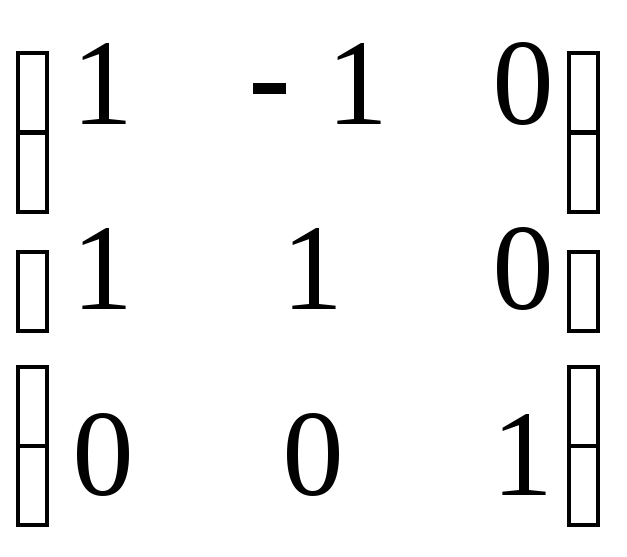 
,
то есть [x] = A[y]
получим A(x,
x) = 2(y1 – y2)(y1 + y2) – 6(y1 + y2)y3 + 2y3(y1 – y2) =
= 2
– 2
– 6y1y3 – 6y2y3 + 2y3y1 – 2y3y2= 2
– 2
– 4y1y3 – 8y3y2.
Поскольку
коэффициент при
не равен нулю, можно выделить квадрат
одного неизвестного, пусть это будет
y1.
Выделим все члены, содержащие y1.
A(x,
x) = 2(
– 2
y1y3) – 2
– 8y3y2 = 2(
– 2
y1y3 + 
) – 2
– 2
– 8y3y2 = 2(y1 – y3)2 – 2
– 2
– 8y3y2.
Выполним преобразование, матрица которого равна B.
z1 = y1 – y3, y1 = z1 + z3,
z2 = y2, y2 = z2,
z3 = y3; y3 = z3.
B =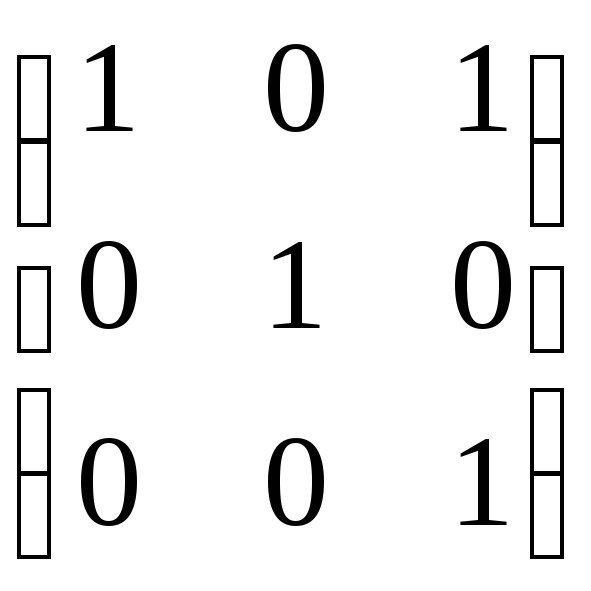 
,
[y] = B[z].
Получим
A(x,
x) = 2
– 2
–
– 8z2z3.
Выделим
члены, содержащие z2.
Имеем
A(x, x) = 2
– 2(
+ 4z2z3) – 2
= 2
– 2(
+ 4z2z3 + 4
) +
+ 8
– 2
= 2
– 2(z2 + 2z3)2 + 6
.
Выполняем преобразование с матрицей C:
t1 = z1, z1 = t1,
t2 = z2 + 2z3, z2 = t2 – 2t3,
t3 = z3; z3 = t3.
C = 
,
[z] = C[t].
Получили:
A(x,
x) = 2
– 2
+ 6
канонический вид квадратичной формы,
при этом [x] = A[y],
[y] = B[z],
[z] = C[t],
отсюда [x] = ABC[t];
ABC =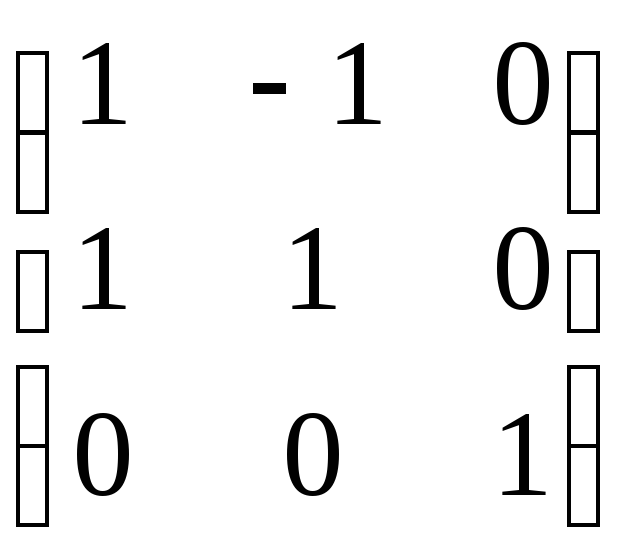 
= 
.
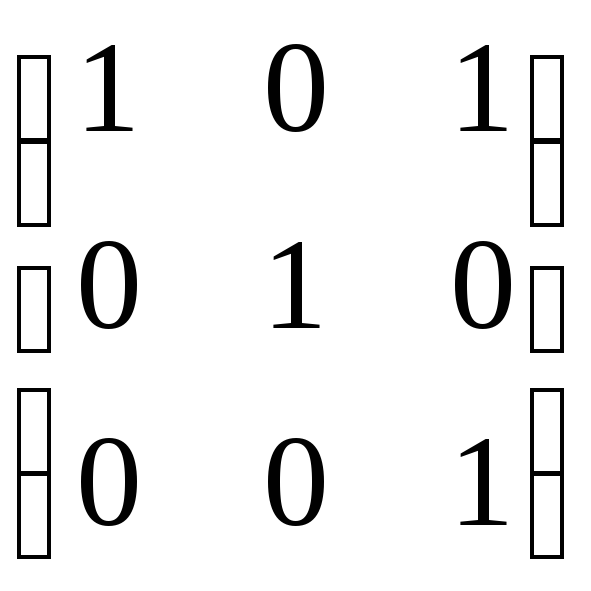
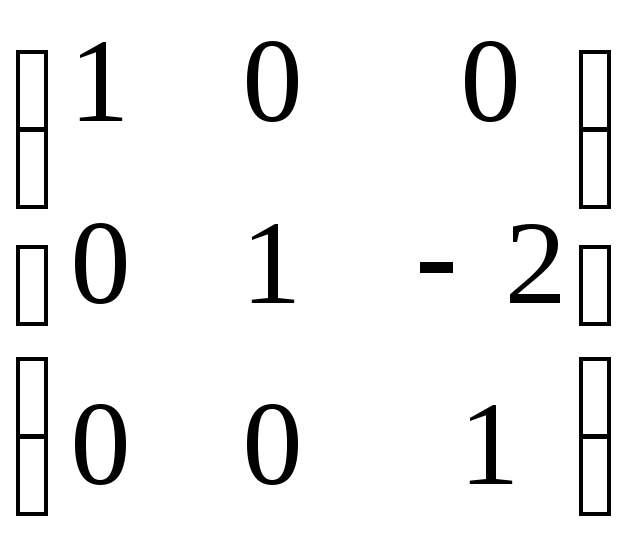Формулы преобразований следующие
x1 = t1 – t2 + t3,
x2 = t1 + t2 – t3,
x3 = t3.