Критерий Сильвестра знакоопределенности квадратичной формы

Пусть форма A(x, x) в базисе e = {e₁, e₂, …, e_n} определяется матрицей A(e) = (a_ij),

A(x, x) = , и пусть ₁ = а₁₁, ₂ = , …, _n = 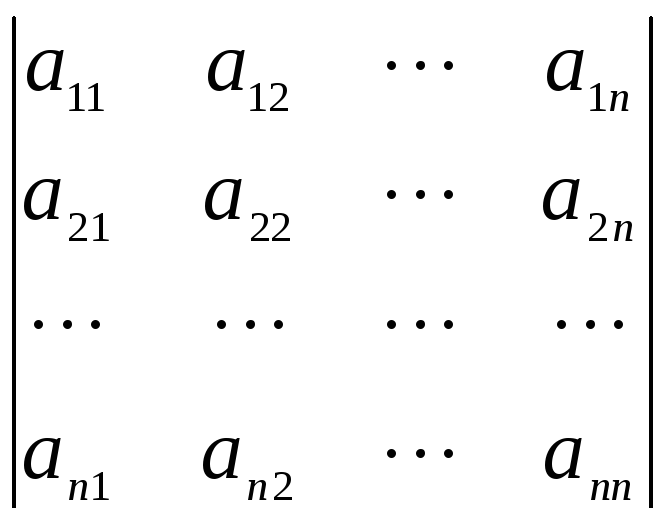 угловые миноры и определители матрицы (a_ij). Тогда справедливо утверждение:

Теорема 11.4 (критерий Сильвестра).

1. Для того чтобы квадратичная форма A(x, x) была положительно определенной, необходимо и достаточно, чтобы были выполнены неравенства: ₁ > 0, ₂ > 0, …, _n > 0.

2. Для того чтобы квадратичная форма A(x, x) была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, причем ₁ < 0.

Пример 11.2. Выяснить, является ли квадратичная форма A(x, x) = 5+ + 5x₃ + 4x₁x₂ – 8x₁x₃ – 4x₂x₃ положительно определенной?

Решение. Составим матрицу этой квадратичной формы:

M =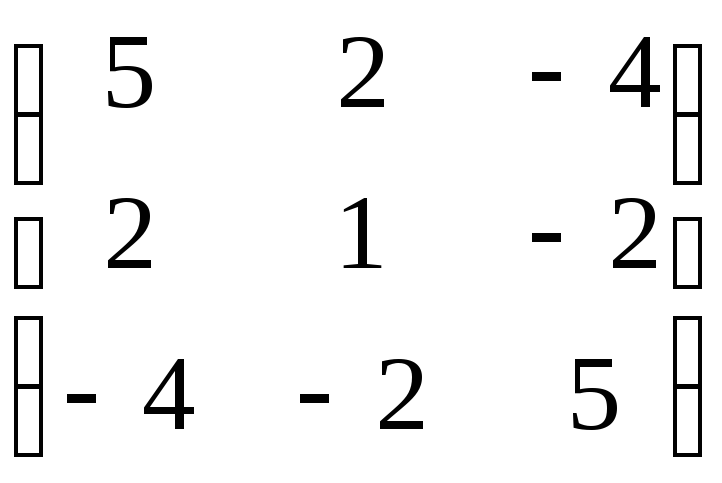 

Вычислим ее угловые миноры:

₁ = 5 > 0,

₂ = = 5 – 4 = 1 > 0,

₃ = 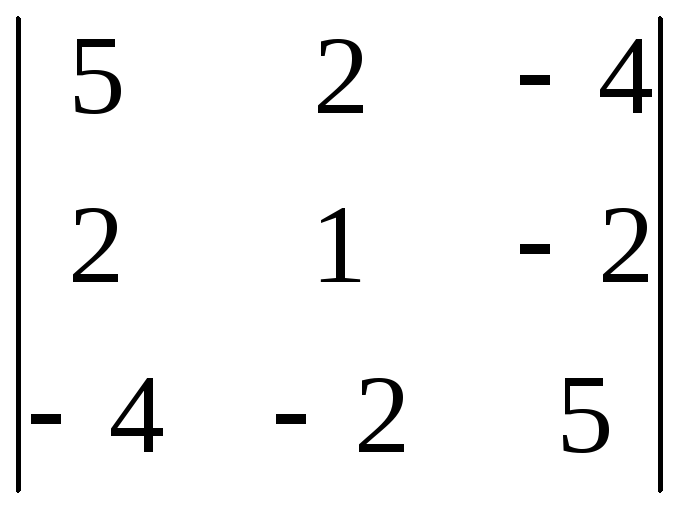= 25 + 16 + 16 – 16 – 20 – 20 = 1 > 0.

Все угловые миноры положительны, следовательно, квадратичная форма положительно определенна.

Пример 11.3. Выяснить, является ли квадратичная форма A(x, x) = 3+ + 5x₃ + 4x₁x₂ – 8x₁x₃ – 4x₂x₃ положительно определенной?

Решение. Составим матрицу этой квадратичной формы:

M =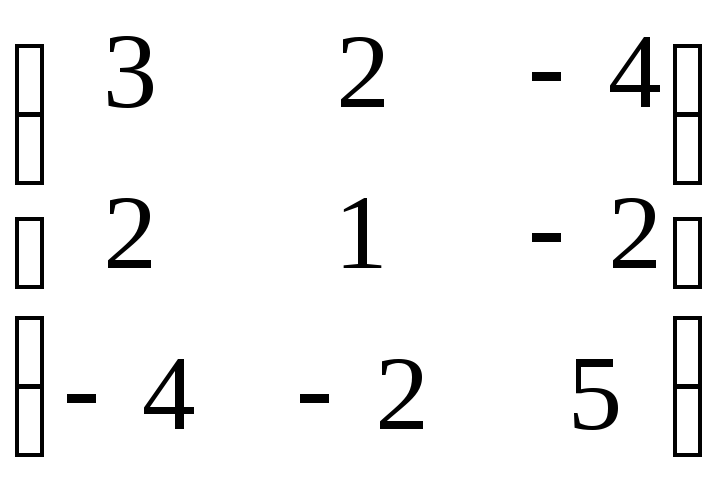 

Вычислим ее угловые миноры:

₁ = 3 > 0,

₂ = = 3 – 4 = –1 < 0,

₃ = 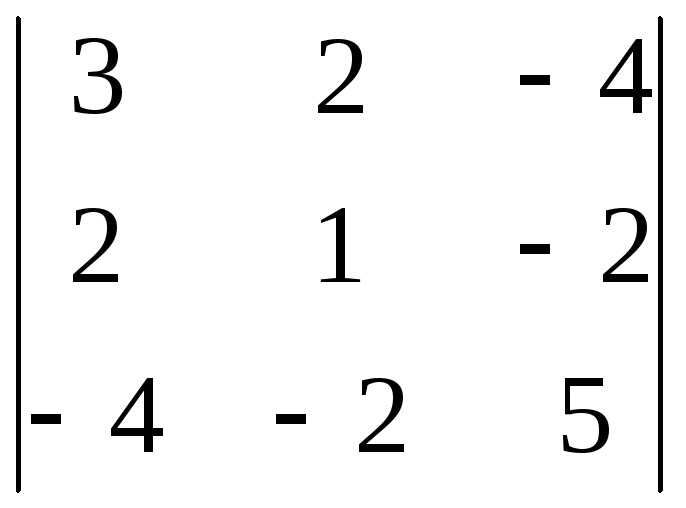= 15 + 16 + 16 – 16 – 12 – 20 = –1 < 0.

Вывод. Квадратичная форма A(x, x) не является положительно определенной, т. к. ₂ < 0, и отрицательно определенной не является, т. к. ₁ > 0, т.о. она знакопеременная.

Заключение

Линейная алгебра является обязательной частью любой программы по высшей математике. Любой другой раздел предполагает наличие знаний, умений и навыков, заложенных во время преподавания этой дисциплины. Данной пособие в доступной, но математически строгой форме, дает возможность освоить все основные понятия и ознакомить с типовыми упражнениями.

Предполагается выпуск задачника по линейной алгебре дополняющего данное пособие. В задачник войдут материалы для проведения практических занятий; заданий для домашних работ, а также практикумы с индивидуальными заданиями для самостоятельного решения.

Библиографический список

Бурмистрова Е.Б., Лобанов С.Г. Линейная алгебра с элементами аналитической геометрии. – М.: Изд-во ВШЭ, 2007.

Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 2006.

Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть I. – М.: ОНИКС 21 век, Мир и образование, 2003.

Ермаков В.И. Сборник задач по высшей математике для экономистов. – М.: Инфра - М, 2009.

Ермаков В.И. Общий курс высшей математики для экономистов. – М.: Инфра - М, 1999.

Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 2002.

Кремер Н.Ш. Высшая математика для экономистов. – М.: Юнити, 2004.

Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989.

Крамор В. С. Алгебра и начало анализа / В. С. Крамор. – М.: Высш. школа, 1981.

Куликов Л. Я. Алгебра и теория чисел: учеб. пособие для педагогических институтов / Л. Я. Куликов. – М.: Высш. школа, 1979.

Куликов Л. Я. Сборник задач по алгебре и теории чисел / Л. Я. Куликов, А. И. Москаленко, А. А. Фомин. – М.: Просвещение, 1993.

Лунгу К. Н. Сборник задач по высшей математике / К. Н. Лунгу. – М.: Айрис-пресс, 2007.

Малыкин В.И. Математика в экономике. – М.: Инфра - М, 2002.

Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Часть I. – М.: Финансы и кредит, 2000.

Фадеев Д.К., Соминский И.С. Задачи по высшей алгебре. – СПб.: Лань, 2001.

Чередникова А. В. Дискретная математика. Теория и практика / А. В. Чередникова, О. Б. Садовская, Л. А. Каминская. – Кострома: Изд-во Костром. гос. технол. ун-та, 2011.

Шапорев С. Д. Дискретная математика. Курс лекций и практических занятий / С. Д. Шапорев. – СПб.: БХВ-Петербург, 2007. – 400с.

Шепелев Ю. П. Дискретная математика: учеб. пособие / Ю. П. Шепелев. – СПб.: Лань, 2008.

Математический энциклопедический словарь / гл. ред. Ю. В. Прохоров; ред. кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. – М.: Сов. энциклопедия, 1988.

Учебное издание

Матыцина Татьяна Николаевна

Коржевина Елена Константиновна