лекции рогов / Рогов_Лекция_ 4

Лекция 4. Симплекс-метод в общем виде

Симплекс-метод в общем виде

Пусть ЗЛП приведена к виду (3), (6) и выполняется условие (5), как в предыдущем разделе (§5. 2). Мы видели, что если в системе (3) свободным переменным присвоить нулевые значения: , то получим допустимое базисное решение этой системы: , а из (6) – соответствующее этому решению значение функции f : .

Следующая теорема определяет критерий, при котором решение является оптимальным решением ЗЛП.

Теорема 1. Если в выражении (6) целевой функции f через свободные переменные все коэффициенты при свободных переменных неположительные, то соответствующее базисное решение является оптимальным и min.

Доказательство. Пусть – произвольное допустимое решение ЗЛП (3), (6), отличное от . Сравним значения функции и . Так как , то среди чисел есть хотя бы одно положительное число. Пусть . Тогда. Из полученного неравенства и следует, что . Теорема доказана.

В следующей теореме определяется условие, при котором ЗЛП не имеет оптимального решения.

Теорема 2. Если в выражении (6) целевой функции через свободные переменные найдется положительный коэффициент и все коэффициенты j-ого столбца в (3) , то ЗЛП не имеет оптимального решения.

Доказательство. Рассмотрим все неотрицательные решения системы линейных уравнений (3), у которых , а . Тогда из (3) получим, что

(9)

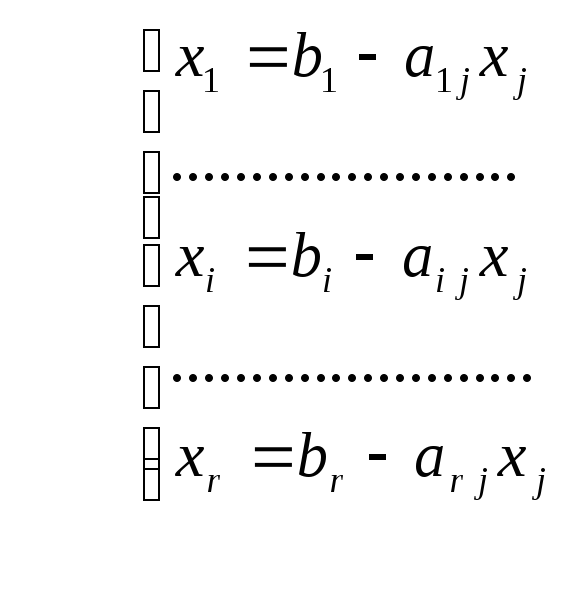
Так как по условию теоремы при k=1, 2, …, r, то равенства (9) можно записать в следующем виде (10):

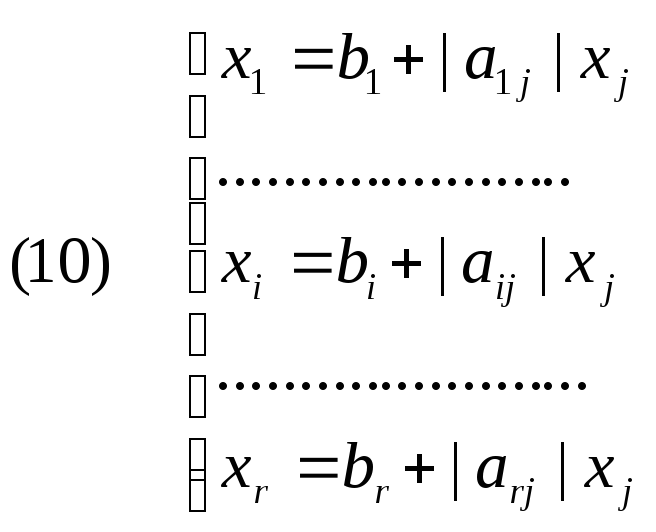
Отсюда ясно, что при любом неотрицательном значении базисные переменные будут принимать неотрицательные значения, т. е. при любом положительном значении мы получим допустимое решение. При этом , и при неограниченном увеличении функция будет неограниченно убывать. Следовательно, ЗЛП не имеет оптимального решения, так как . Теорема доказана.

Теорема 3 позволяет выяснить, при каком условии существует симплексное преобразование, позволяющее от данного допустимого базисного решения перейти к новому допустимому базисному решению такому, что .

Теорема 3. Если в выражении целевой функции f через свободные переменные найдется коэффициент при свободной переменной и среди коэффициентов в системе (3) есть положительные, то при соответствующем симплексном преобразовании получается такое допустимое базисное решение , что .

Доказательство. Разрешающий элемент выберем, используя условие (8) из раздела §5.2. Тогда новая базисная переменная . В новом базисном решении переменная примет значение : .

Придавая новым свободным переменным нулевые значения в выражении (6) и учитывая неравенства: , , получаем .

Мы видим, что новое допустимое базисное решение обладает требуемым свойством : . Теорема доказана.

Так как рассмотренный упорядоченный перебор допустимых базисных решений конечен, то, используя этот метод, через конечное число шагов либо найдем оптимальное базисное решение, либо обнаружим, что ЗЛП не имеет оптимального решения,

Пример. Рассмотрим задачу о распределении ресурсов в канонической форме. Дана система линейных уравнений:

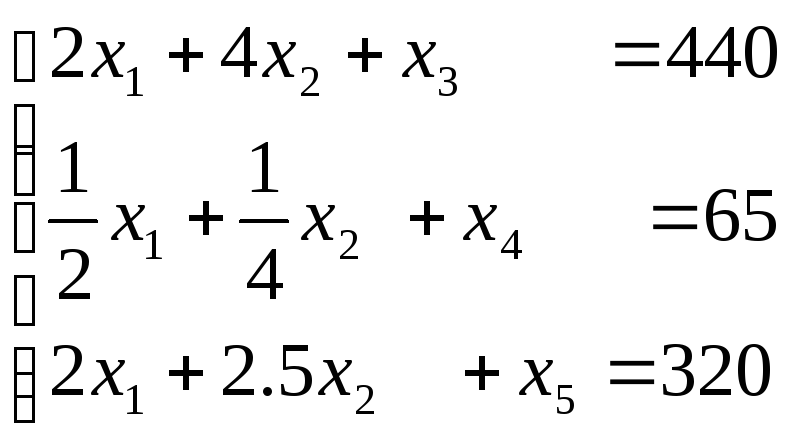
Нужно найти неотрицательное решение системы, при котором целевая функция принимает наименьшее значение.

Решение. Определитель матрицы, составленной из коэффициентов при переменных отличен от нуля, поэтому ранг r системы равен трем: r = 3, и переменные являются базисными, свободные переменные. Заданная система уравнений имеет вид (3), свободные члены – положительные (т.е. выполняется условие (5)), функцию легко записать в виде (6): .

Положив , получим начальное допустимое базисное решение и . Составим симплекс-таблицу:

Переменные Базис						Свободные члены
	2		1	0	0	440
			0	1	0	65
	2	2.5	0	0	1	320
f	8	12	0	0	0	0

Применим теперь теоремы 1, 2, 3. Просматривая коэффициенты последней строки (т.е. коэффициенты у свободных переменных в функции ), замечаем, что, например, коэффициент при равен 12 > 0. Отметим второй столбец стрелкой сверху и выберем а этом столбце разрешающий элемент, используя условие (7): . Значит, коэффициент 4 является разрешающим. Отметим первую строку слева стрелкой. Для наглядности выделим разрешающий элемент 4 дугой окружности. Стрелки указывают, что базисную переменную надо заменить в базисе на свободную переменную .

Выполним теперь соответствующее симплексное преобразование с полученной таблицей. Для этого разделим первую строку на разрешающий элемент 4 и с помощью полученной после деления строки, умножая ее на подходящий множитель и прибавляя к другой строке, сделаем во втором столбце нули во всех строках, кроме первой (как при применении метода Гаусса). Например, умножим после деления новую первую строку на и сложим со второй строкой. Эти действия переведут переменную в базис, а переменную сделают свободной переменной.

После этого мы получим новую симплекс-таблицу. В ней базисная переменная заменена переменной . Новая таблица имеет вид:

Переменные Базис						Свободные члены
	0.5	1		0	0	110
		0		1	0
		0		0	1	45
f	2	0	–3	0	0	–1320

Мы получили новый базис и соответствующее допустимое базисное решение . Так как коэффициент =2 > 0 при свободной переменной в выражении , то по теореме 1 решение не является оптимальным. Отметим первый столбец стрелкой сверху и выберем а этом столбце разрешающий элемент: . Поэтому – разрешающий элемент. С помощью симплексного преобразования заменим в базисе на . Для этого третью строку делим на разрешающий элемент и с помощью новой третьей строки преобразуем остальные строки так, чтобы в столбце получились нули. Получим новую симплекс-таблицу:

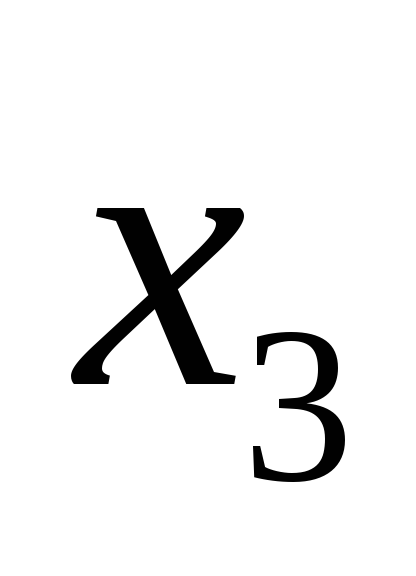
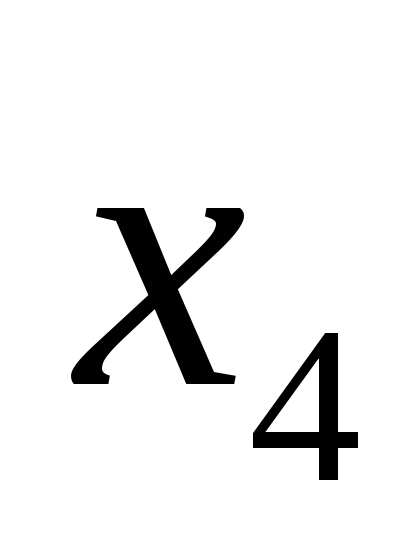
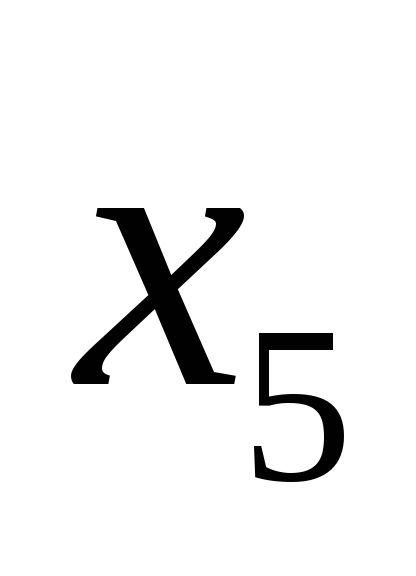
Переменные Базис						Свободные члены
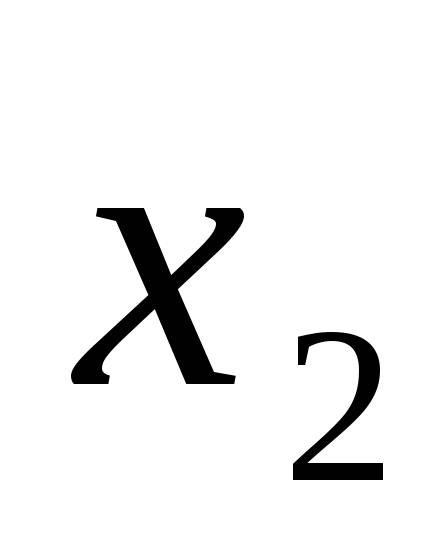
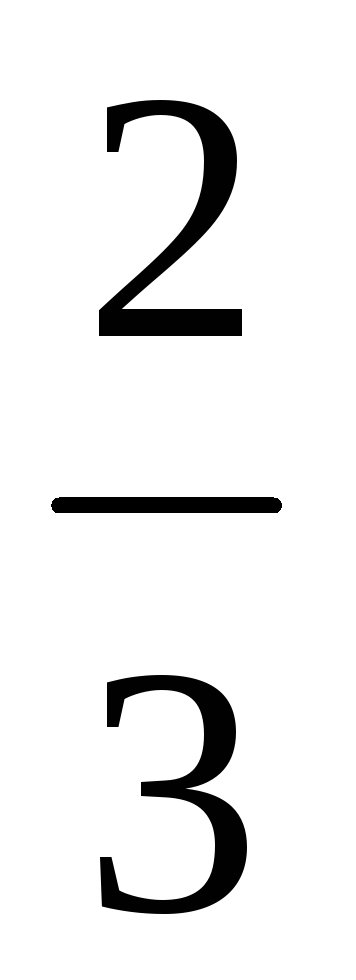
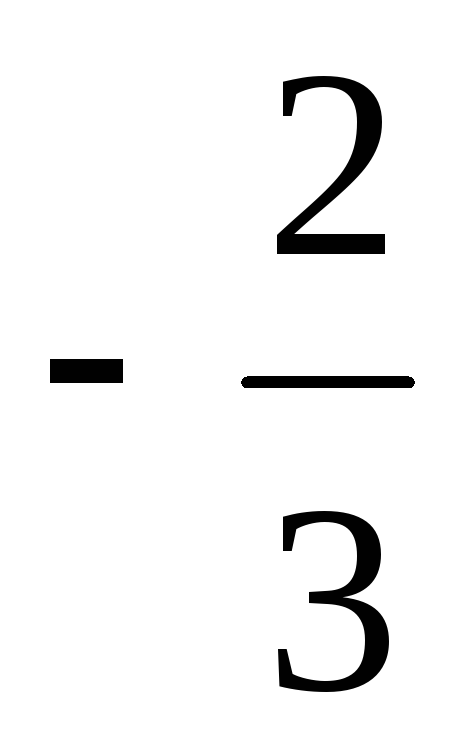
	0	1		0		80
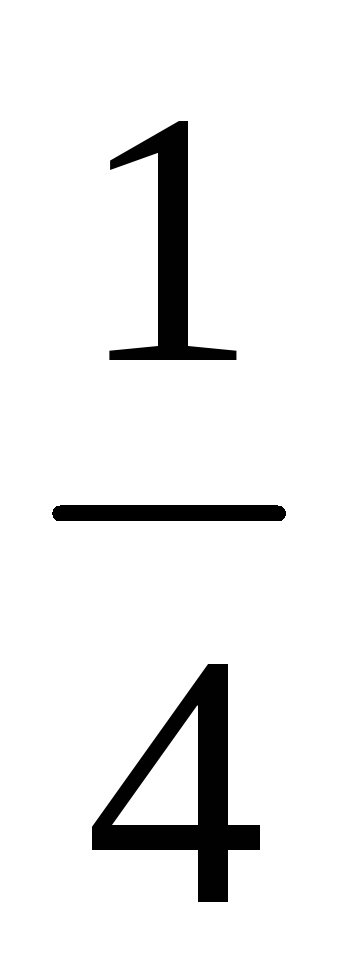
	0	0		1		15
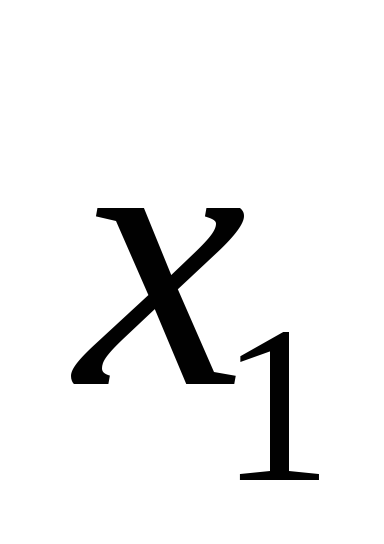
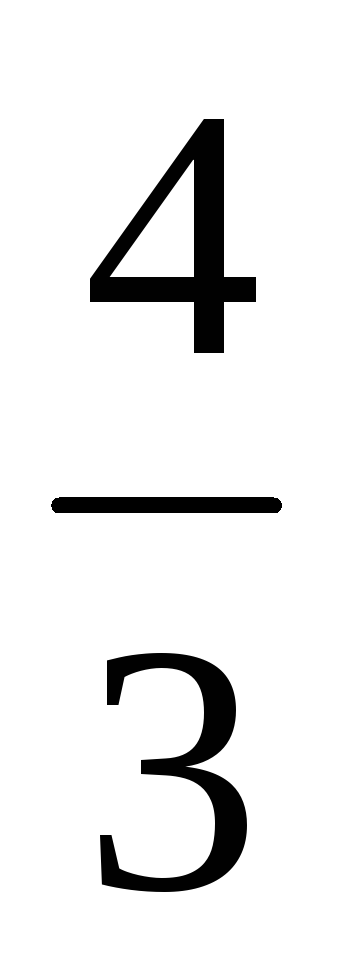
	1	0		0		60
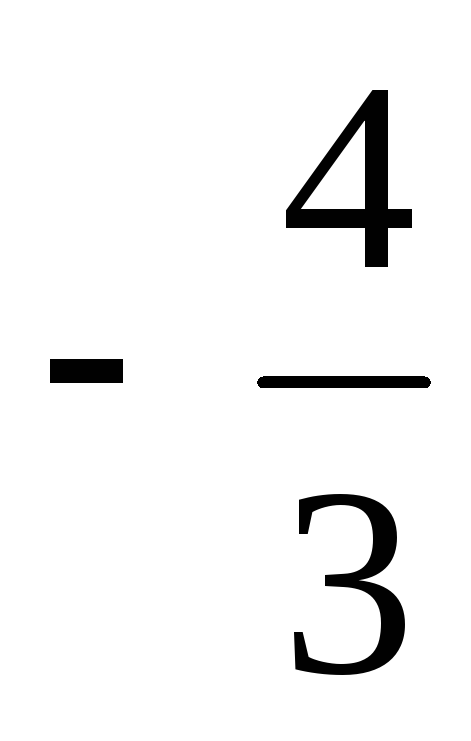
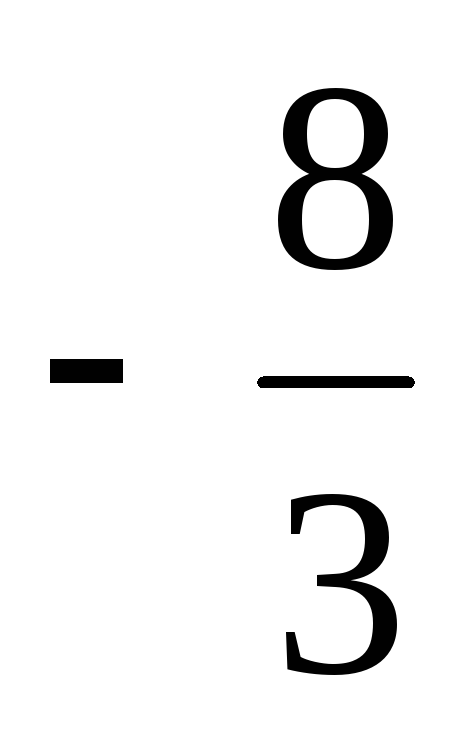
f	0	0		0		–1440

Новый базис – , ему соответствует допустимое базисное решение, и .

В последней строке таблицы нет положительных коэффициентов, поэтому по теореме (1) – оптимальное решение и min = .

Сформулируем правила решения ЗЛП симплекс–методом с использованием симплекс–таблиц:

1. Каким-либо способом (один из методов будет описан в следующем разделе) найти базис и общее решение системы ограничений ЗЛП, в котором все свободные члены неотрицательны. Выразить функцию через свободные переменные. Составить первую симплекс-таблицу и найти допустимое базисное решение. Перейти к правилу 2.

2. Просмотреть коэффициенты при свободных пременных в последней (для ) строке таблицы. Если все эти коэффициенты , то (по теореме 1) соответствующее базисное решение Б является оптимальным и . Задача решена. В противном случае перейти к правилу 3.

3. В последней строке есть положительный коэффициент у свободной переменной . Отметить j – тый столбец стрелкой и просмотреть коэффициенты j-ого столбца. Если все , то по теореме 2 ЗЛП не имеет оптимального решения, решение задачи закончено. В противном случае перейти к правилу 4.

4. Среди коэффициентов в системе (3) есть положительные. Найти , объявить элемент разрешающим и отметить стрелкой i-ю строку. Перейти к правилу 5.

5. Выполнить симплексное преобразование, заменив на в базисе. Построить новую симплекс-таблицу. Найти новое базисное решение и перейти к правилу 2.

Работу закончить, если либо выполняется условие теоремы 1 (правило 2), либо выполняется условие теоремы 2 (правило 3).