
ГОС математика / Геометрия / 7_8_9
.doc|
Вопрос 7. Поверхности второго порядка. Опр. Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида:
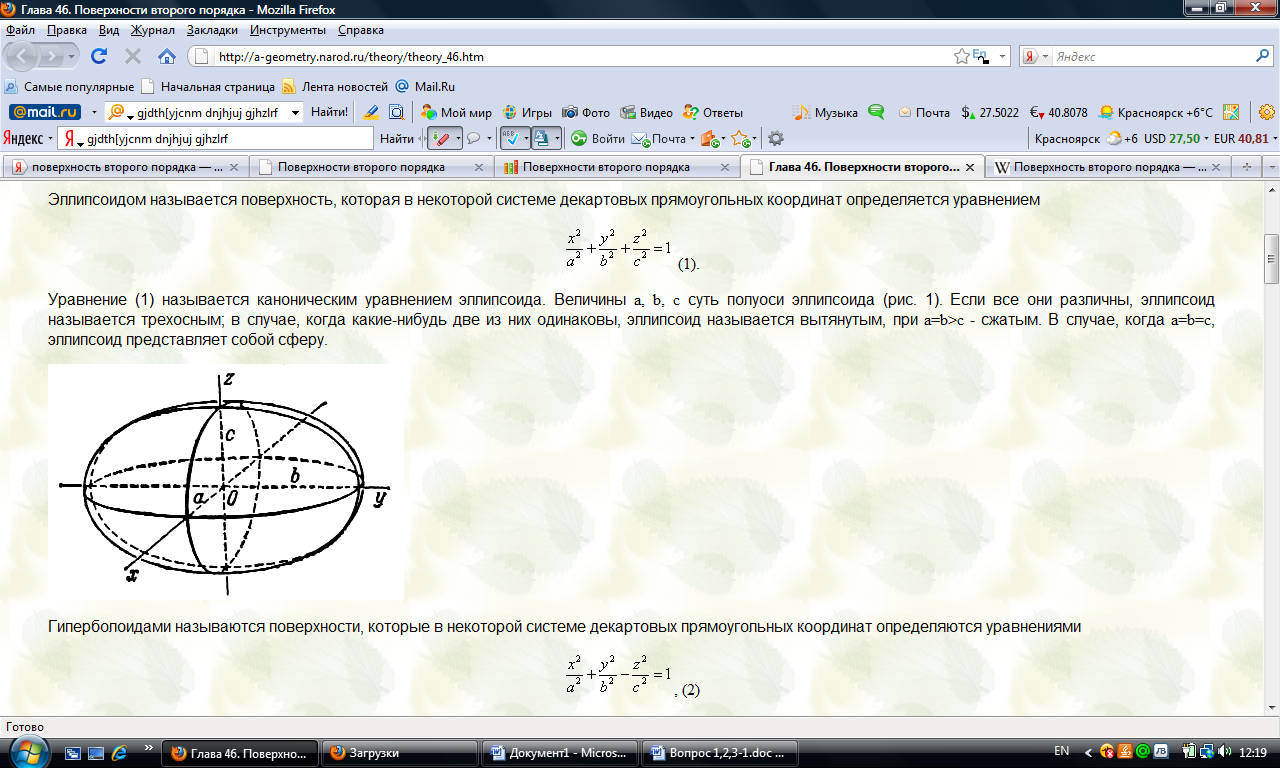
в к-ом, по крайней мере один из коэф-ов a11, a22, a33, a12, a23, a13 отличен от нуля. Ур-ие (1) может быть преобразовано с помощью параллельного переноса и поворота системы координат (относительно одной из коор-х прямых) к следующему виду: эллипсоид:
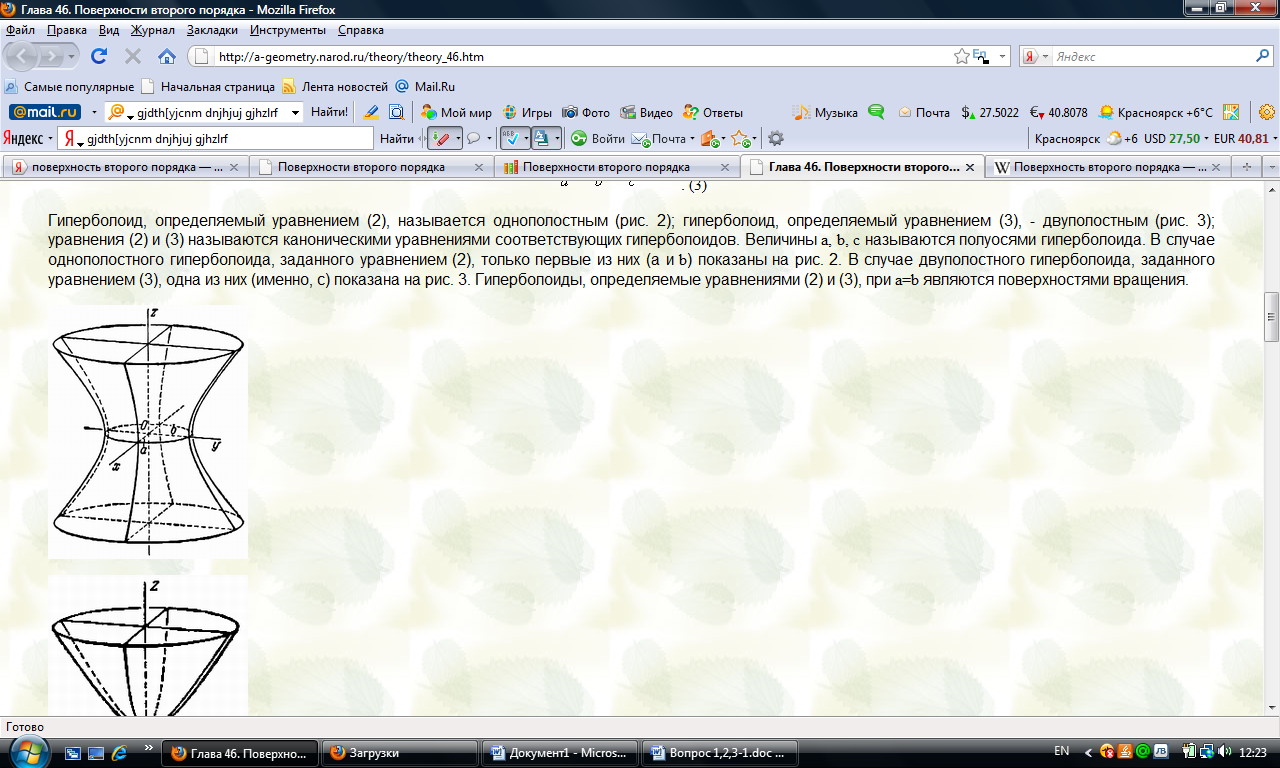
однополосной гиперболоид : Для построения гиперболоида найдем его сечения различными плоскостями. C ХОУ, то есть z=0, получим уравнение эллипса. Аналогично строим остальные кривые
двуполостной гиперболоид:
Величины a, b, c наз-ся полуосями эллипсоида и гиперболоида.
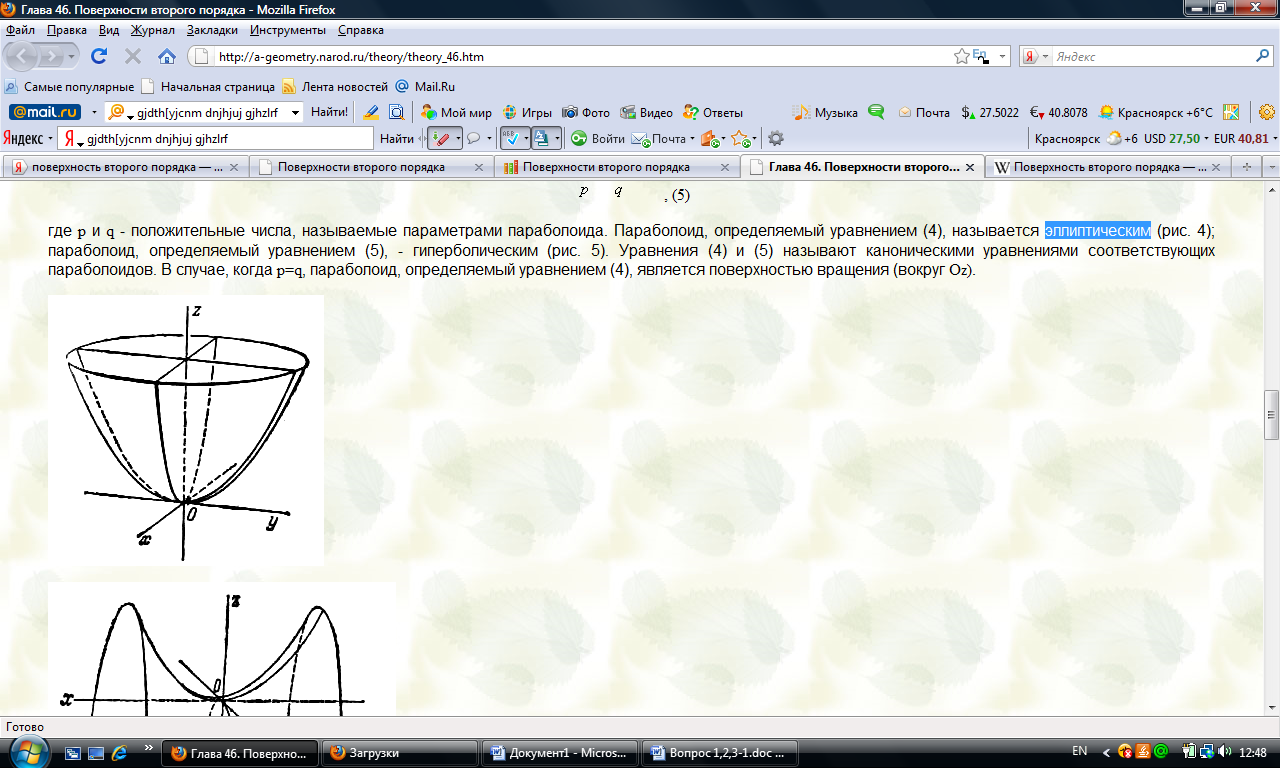
эллиптическим параболоид:
гиперболическим параболоид:
где p и q - положительные числа, наз-ые параметрами параболоида.
С в начале координат: x2+y2+z2=R
Опр. Конической поверхностью – наз-ся поверхность полученная движением образующей с фиксированной точкой вдоль направляющей. Опр. Цилиндрической поверхностью наз-ся геометрическое место параллельных прямых, пересекающих данную линию. Эта линия наз-ся направляющей, а параллельные прямые – образующими. Поверхность, к-ая задается уравнением:
1)
2)
3)
Пример:
1.
1) Пусть x=0,
тогда
2) z=2
2. Эллипсоид
проходит ч/з точку
Решение:
x2+8y2-8=0 |:8
Подставим
|
Вопрос 8. Движение плоскости. Классификация движении. Опр. Говорят, что задано отображение f множества Р в множество Q, если каждому элементу множества Р поставлен в соответсвие некоторый элемент из Q f – это правило по которому эл-ту множ Р поставлен в соотв некий элемент мн-ва Q. Тогда q bp Q - это образ р, а р- прообраз q и записывают f(p)=q или q – есть образ р при отображении f Опр. Движением плоскости (пространства) называется преобразование, сохраняющее расстояния между точками. - движение плоскости (пространства), если для любых точек М и N этой плоскости (пространства) MN=M1N1, где (М) =М1, (N) =N1. Пр.1.Тождествеенное преобразование, осевая симметрия, поворот плоскости вокруг точки, ||-й перенос, скользящая симметрия являются движениями. Основные свойства.
Движение мы
определили как преобразование,
сохраняющее расстояния между точками.
Это позволяет найти другие свойства
фигур, не меняющиеся при движении.
Будем использовать следующие
обозначения: точки А,
В, С, D,
M,
P,
N,
прямые а,
b,
векторы
1) Если В лежит между точками А и С, то В1 лежит между точками А1 и C1. 2) Движение отрезок, луч, прямую отображает соответственно на отрезок, луч, прямую. 3) Если точки А, В, С не лежат на одной прямой, то точки А1, В1, С1 также не лежат на одной прямой. 4) Движение пространства отображает плоскость на плоскость. 5) При движении сохраняется параллельность прямых. 6) При движении сохраняется величина угла.
7)
При движении вектор
Опр. Осевая симметрия. Преобразование плоскости, при котором любая точка некоторой фиксированной прямой m отображается на себя, а любая другая точка M отображается на такую точку M1, что отрезок MM1 перпендикулярен прямой m и делится ею пополам, наз. осевой симметрией, или отражением от оcи m. Свойства:
Опр. Поворот. Поворотом плоскости вокруг точки О на ориентир угол φ наз-ся преобразование плоскости при котором точка О отображается на себя, а любая др точка отобр-ся на такую точку М1, что ОМ=ОМ1 и угол <MOM1=φ Поворот задается центром поворота и углом поворота Свойства:
Опр.
Параллельный
перенос. Дан
вектор
Свойства:
Опр.
Скользящая
симметрия.
Рассмотрим на плоскости параллельный
перенос α, определяемый вектором
Пр.2. Гомотетия, движением не является. Она является движением только при к = 1. Опр. Гомотетией наз.преобразование пл-ти, при котором фиксированная точка S отображается на себя, а любая другая точка M отображается на такую точку М1, что выполняется равенство SM1=kSM, где k – фиксированная для данного преобразования число, отличное от 0. Теорема. Множество всех движений плоскости (пространства) является группой. Опр. Фигуры F и F1 наз. равными, если существует движение, отображающее F на F1. Пишут F = F1.
Свойства движений имеющие неподвижные точки. Вид движения можно характеризовать множеством его неподвижных точек. Выделим некоторые свойства движений плоскости, имеющих неподвижные точки. 1.1) Если движение имеет две неподвижные точки А и В, то все точки прямой АВ неподвижны. 1.2) Если движение имеет три неподвижные неколлинеарные точки А, В, С, то есть тождественное преобразование. 1.3) Если движение имеет две неподвижные точки А и В, то есть либо тождественное преобразование, либо осевая симметрия. Сформулируем основную ТЕОРЕМУ движений
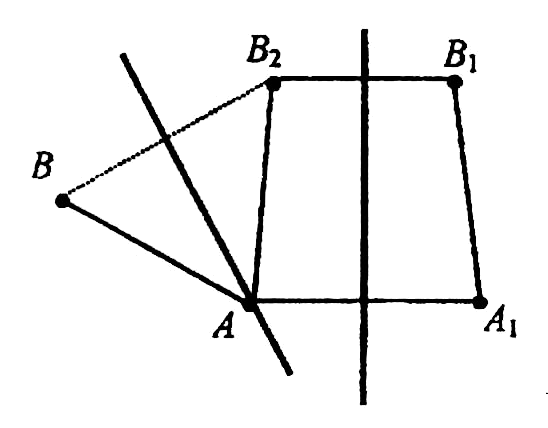
Т 1. Всякое движение плоскости можно представить в виде композиции не более трех осевых симметрии.
Д Пусть движение отображает точки А и В на точки А1 и В1 Попытаемся с помощью осевых симметрии вернуть точки А1 а В1 в первоначальное положение. Рассмотрим осевую симметрию 1, которая точку А1 отображает на точку А. Ось симметрии является серединным перпендикуляром к отрезку АА1. При этом точка В1 отобразится на точку В2. АВ1=АВ2 Рассмотрим осевую симметрию σ2, которая отбражает точку А в точку А, а точку В2 в точку В. Ось симметрии является серединным перпендикуляром к прямой ВВ2 Рассмотрим движение •1•2 (по св-ву 1.3).Получим: А→А1→А→А также В→В1→В2→В То есть А→А и В→В то есть преобразование либо ТП либо σАВ Если •1•2 = , то, умножив это равенство справа на 2•1 получим, что = 2•1 (учитываем, что 2•2=1•1=). композиция двух осевых симметрий Если •1•2=, то таким же способом приходим к равенству = 2•1•. Итак, в первом случае данное движение есть композиция двух симметрии, во втором - трех. Ч.Т.Д. Учитывая результат этой теоремы, можно описать все виды движений. Выясним, какие движения получаются в результате композиции двух и трех осевых симметрии. Все движения можно разбить на два класса. Движения первого рода. Сюда относятся движения, полученные в виде композиции двух симметрии. Они не меняют ориентацию фигур на плоскости. Действительно, при осевой симметрии ориентация фигуры меняется на противоположную, значит, четное число симметрии не меняет ориентацию фигуры. Движения второго рода. Это движения, представленные композицией трех осевых симметрии, и сами осевые симметрии. Они меняют ориентацию фигур. Т2. Всякое движение первого рода есть либо параллельный перенос, либо поворот. Т3. Всякое движение второго рода есть либо осевая, либо скользящая симметрия.
|
Вопрос 9. Аффинные преобразования плоскости. Родство.
Опр.
Преобразование
плоскости, сохраняющее прямолинейность
и простое отношение трех точек прямой
Основные св-ва аффинных преобразований, имеющих неподвижные точки 1. Неколлинеарные точки отображаются в неколлинеарные точки 2. Прямая отображается на прямую, луч на луч, отрезок на отрезок 3 Парал-ые прямые отбр-ся на парал-ые прямые 4 плоскость отбр-ся на плоскость 5 вектор на вектор 6 величина угла в общем случае не сохраняется 7 Сохраняется отношение площадей фигур 8 Если две точки А и В двойные или не подвижные, то все точки прямой АВ будут двойными(неподв) 9 если аф преобр имеет три неподв некол точки, то f- будет ТП Опр. Неподвижное аффинное преобраз-е пл-ти, имеющее неподвижные точки А и В, называется родственным преобраз-ем или родством (прямая АВ наз-ся осью родства). Т к Родство частный случай аф пре-я, то оно обладает всеми св-ми аф преоб-я Основные св-ва родства(частные):
Точка С принадлежит АВ, то σ(С)=С1, так как родство аф преоб-е Пусть D не принад-т АВ, то D→D1 и если σ=е(ТП) то по свойству 9 аф преоб-я приходим к противоречию
Дано: m-ось р-а, а парал-на m, Ро(а)=а1 Докажем, что а1 парал-на m. Итак, предположим, что а1 пересекает m в точке Q. Тогда σ- -1 m (Q1)=Q, отсюда Q принадлежит а и Q принад-т m. А это противоречит условию задачи, значит а1 парал-на m
б) АА1 пересекает m в точке Q, AA1=AQ→A1Q=AA1 б) АА1=a, a парл-на m. Пусть Родство с осью m прямую а→а, а содержит А1. а1 парал-на m(св-во3) значит а=АА1=a1
M –ось родства. В принад-тАА1, АА1 пересекает m в точке Q. Ро m(Q)=Q=Q, а Ро m (В)=В1 принадлежит АА1
Пусть В не принадлежит АА1, тогда В1= Ро m (B) Пусть АА1 пересекает ВВ1 в точке Q, Q принадл АА1 и Ро (АА1)=АА1, значит Q→Q1 при Ро с m. Но Q принадлежит ВВ1 и Ро m (ВВ1)=ВВ1, т еQ→Q принад-т ВВ1
Значит Q принад-т пересечению АА1 и ВВ1 Q=Q1 неподвижна и M – ось родства неподв-я прямая, Q не прин-т m, Значит родство = е, противоречие с опред родства, значит не верно что мы предположили пересечение прямых
Т1. Если
на плоскости π заданы прямая m
и две точки А
и А1,
не лежащие на m,
то существует единственное родство,
где m-
ось,
Т2. Существует и единственное аффинное преобразование, которое три неколлинеарные точки А, В ,С на три неколлинеарные точки А1, В1, С1.
Д-во.
Пусть даны точки А,
В,
С
не лежащие на одной прямой, и А1,
В1,
С1
не лежащие на одной прямой. Рассмотрим
подобие π,
которое A→A1,
B→B1,
при этом С→С2.
Если С2
и С1
различны, то зададим родство ρ
с осью А1В1,
которое отображает С2
на С1.
Композиция преобразований π
и ρ
есть аффинное преобразование α,
которое А,
В,
С
отображает на А1,
В1,
С1.
Д-ем единственность α.
Пусть α1
А,
В,
С
отображает на А1,
В1,
С1,
тогда
Следствие. Всякое аффинное преобразование пл-ти можно представить в виде композиции подобия и родства (если оно само не подобие и не родство). Примеры:
д 1) AB 2) s∩AB=K 3) KA1 4) с т.B пр.‖‖AA1 5) KA1∩BB1=B1
АА1 пересекает S в точке S1 = середине АA1.В-произв Точка лежащая по др сторону от оси. Построить В1
1) AB 2) s∩AB=M 3) MA1 4) с т.B пр.// AA1 5) MA1∩BB1=B1
Пример3 Аналогично 2 примеру
2) т.C – произвол. 3) AC 4) s∩AC=L 5) A1L 6) CC1//AA1,CC1∩A1L=C1 7) A1C, A1C∩s=N 8) C1N∩AA1=B1
|



 фера
радиуса R
с центром
фера
радиуса R
с центром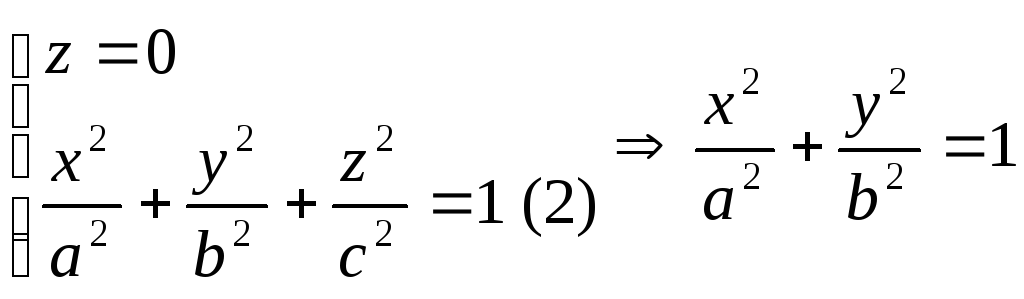
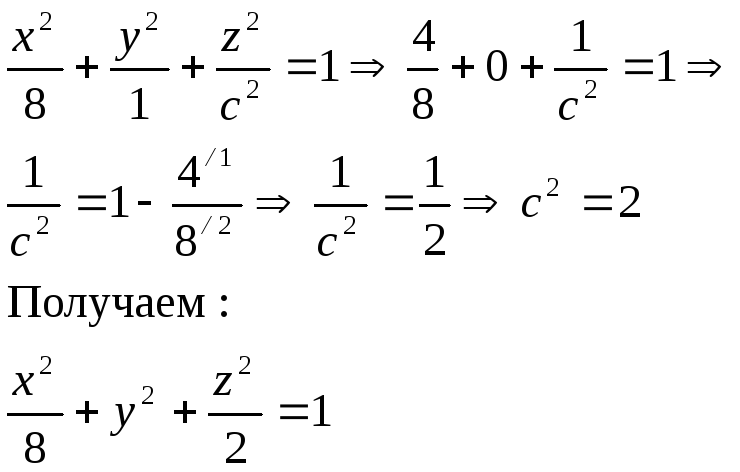
 оказательство.
оказательство.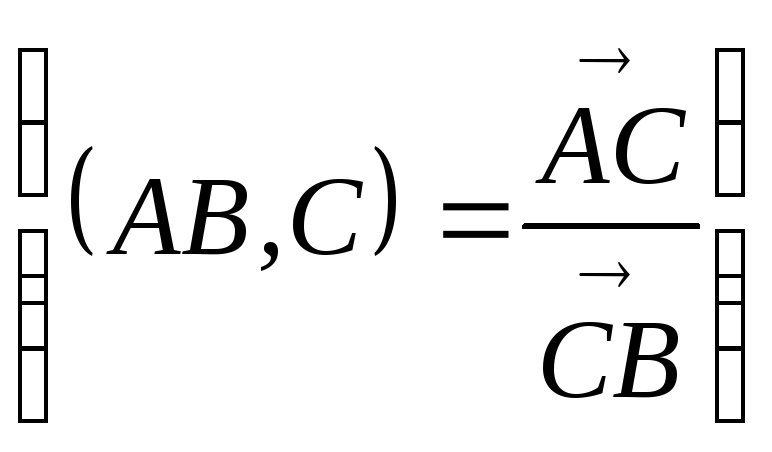 ,
называется аффинным.
,
называется аффинным.
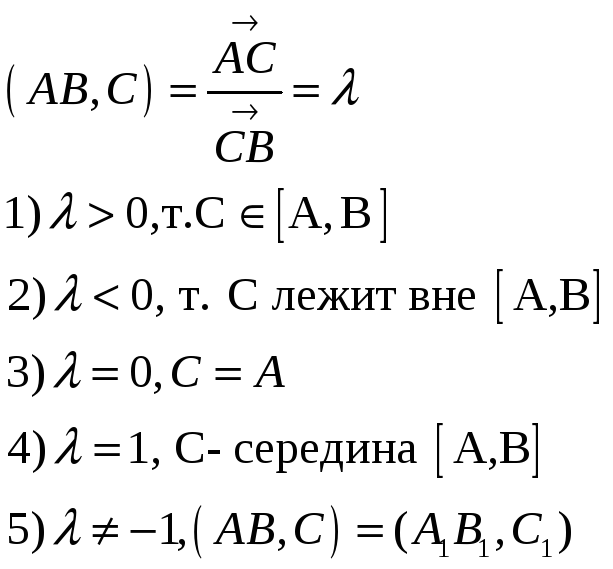
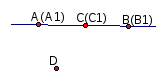 σ(родство)А→А1=А,В→В1=В
σ(родство)А→А1=А,В→В1=В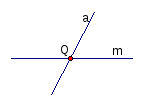 m-ось
родства, пересекает M
в точке Q.
σ m(Q)
= Q1=Q
; σm
(a)=a1,
тогда а1 содержит точку Q1=Q,
значит а1 перес-т а в точке Q
m-ось
родства, пересекает M
в точке Q.
σ m(Q)
= Q1=Q
; σm
(a)=a1,
тогда а1 содержит точку Q1=Q,
значит а1 перес-т а в точке Q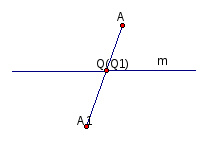
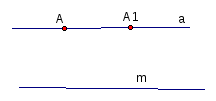

 ано
s- ось родства, А и А1 соответсвенные
точки в родстве, В произвольная точка
плоскости. Построить В1 такую, что Ро
от s (B)
ано
s- ось родства, А и А1 соответсвенные
точки в родстве, В произвольная точка
плоскости. Построить В1 такую, что Ро
от s (B)
 1)
A1=B
1)
A1=B