
ГОС математика / Алгебра / GOSy_Algebra_1
.doc|
8. Базис и размерность конечн.векторн.прост-ва. Опр.
Вектор
Опр.
Система векторов
Опр.
Система векторов
Пусть
дана система векторов
Опр.
Базисом непустого множества векторов
Пр-р
1:
док-м, что базисом всего арифм-кого
n-мерного
векторного простр-ва является система
так называемых единич. векторов
Очевидно,
для любого вектора
Теорема
(о
Д-во:
#По условию в
произвольн
вектор из S.
Образуем подсистему В':
Теорема. Любые два базиса одной сист.векторов состоят из один-го числа векторов
Док-во:#
Будем раасм-ть только базисы,состоящ.из
конечн.числа векторов. Возьмем два
базиса
Т.к
(в) тоже базис, то
r>s-неверно (рассуждения аналогичные,меняем только местами (а) и (в). Получаем что предположения о том, что r<s и r>s – неверны, значит r=s. Пр-р 2: (1,2,5)=а1,(3,6,15)=а2, Базис (1,2,5), т.к 3а1=а2-Л.З. Опр. Рангом конечной системы векторов, содержащей ненулевой вектор, наз-ся кол-во (число) векторов ее базиса. См.Пример 2: rang=1,т.к. в базисе только 1 вектор. -Если конечная система, состоит только из нулевых векторов, то она не имеет базиса, поэтому считаем ее ранг равным нулю. Ранг-есть размерность векторн.прос-ва.
Опр:
Базисом пространства
1) В-ЛНЗ
2)
Любой вектор из
Теорема.
В произвольном векторном пространстве
для любой системы векторов
Док-во.
Идя по данной системе векторов
След 1. Всякая конечная система векторов, содержащая ненулевой вектор, имеет базис, и любые два базиса этой системы содержат одинаковое кол-во векторов. След 2. Всякую ЛНЗ систему векторов конечно порожденного векторного пространства можно дополнить до базиса этого пространства.
След
3.
Пусть V
— конечно порожденное векторное
пространство. Для любого ненулевого
подпространства А, отличного от V,
сущ-ет подпространство В {называемое
дополнением к А) такое, что
Опр: Векторное пространство V над полем Р наз-ся n-мерным, если оно имеет базис из n векторов. При этом, n наз-ся размерностью векторного прос-ва V. Обозн: dimV=n. Размерность нулевого пространства считаем равной 0. |
1. Кольцо целых чисел. Теорема о делении с остатком. НОД и НОК двух целых чисел. Опр. Кольцом наз.мн-во элементов К, на кот-ом определены операции сложении и умножения, причем выполнены след условия:
1)
«+» коммут (а+b)+с=а+(b+c)
и ассоц а+в=в+а для любых а,b,с
2)Суш-ет
эл-т 0
3)для
любого а
4)
«*» ассоц:(а*b)*с=а*(b*с)
для любых а,b,c
5)
«*» дистриб относительно сложен
а*(b+с)= а*b+а*с для любых а,b,c
Если
«*»в кольце коммун, то кольцо- коммун-ое.
Кольцо К-кольцо с единицей,если сущ
элемент е
Пример:Z,Q,R-ассоц
кольца(К-числовое множ-во явл-cя кольцом
a,b Свойства:
1)Для
любого эл-та а
Док-во: а*0=а(0+0)=а*0+а*0 => а*0=а*0+а*0 прибавим к обеим частям -(а*0), получим 0=а*0 Так же док-ся, что 0*а=0
2)Для
любых эл-ов а и b
Вычитанием
в кольце К наз бинарная операция- :
а-b+а+(-b) для любых а,b
3)Умнож в кольце дистриб относ-но вычитания :(а-b)с=ас-bс. Док-во: используя опр «-», дистриб «*»относ «+» и св-ом 2:(а-b)с=(а+(-b))с=ас+(-b)с=ас+(-(b))=ас-bс.
Опр:!
К=К,
+,*-Кольцо
Н=Н,
+,*.Алгебра
Н- подкольцо кольца К, если 1)НК,
а-b
Опр. Системой целых чисел называется кольцо <Z,+,*> c основным элем Z, элементы которого называются целыми числами, причем выполняются след условия: 1)<N,+,*><Z,+,*>;2)Z=N{0}-N, где –N={-n|nN}. Опр:a>bb-aN, a,b Z-отношение «меньше». Отношение «меньше» обладает следущими св-ми:1)Св-во транзитивности:a<b,b<ca<c;2)св-во трихотомии: aZ, bZ одно и только одно из трех либоa<b либо a=b либо b<a a-bZ=-N{0}N Кроме того «+» и «*» монотонны:1)монот «+»a<ba+c<b+c;2)a<b,c<0 ac<bc Опр: Разделить цел число а на число b0 с остатком это значит найти такие целые числа q,r из Z, что a=bq+r и |b|>r 0, при этом q-неполное частног, r- остаток.
Теорема
(о
делении с остатком)
Деление с остатком всегда возможно и
однозначно.(
а, bZ,b0
,
q
и гZ
:a=bq+r,
где
# Рассмотрим два случая.
Рассмотрим числовую прямую, разобьем ее на отрезки длины b
Ясно,
что число
a
попадет в один из этих отрезков. Будем
считать, что a
может совпадать только с левым концом
отрезка, в противном случае возьмем
следующий отрезок. Т.е.
2)
b<0,
но тогда –b>0.
Тогда по 1) a=(-b)q+r,
где
Док-ем единственность.
Пусть
a
= bq+r
и
b(q-
q1)=
r1-r.
Если q=q1 Предположим,
что
НОД
Опр.
Число d
наз. ОД чисел а и b,
если a
Опр. Число d наз HOД чисел а и b. если d- общий делитель и делится на любой общий делитель d-НОД-
1.d>0;
2.a Св-во:
1.Если
a
#1)b>0-по
усл. 2)a
3)
пусть a Лемма: Если числа a.b,q,r связаны рав-вом a=bq+r, то (a,b)=(b,r) # Пусть (a.b)=d1, (b,r)=b2
1)
a
2)
(b.r)=
d2:=>b Алгоритм Евклида(сп-б нах-я НОД): Состоит из 2-х шагов: 1)делим а на b, если деление нацело, то (a.b)=b;
2)если
a
a=bq0+r0 ,0 r0|b| b= r0q1+r1 , 0 r1| r0| r0= r1q2+r2, 0 r2| r1| … rn-2= rn-1qn+rn, 0 rn| rn-1| rkn= rnqn+1(rn+1=0) 0 rn |rn-1| |rn-2| … |r2| |r1| |r0| |b| Эта цепочка остатков конечна, т.к. это убыв. посл-ть N-чисел, огран-ая снизу нулём. След-но, алг Евклида конечен.
Теорема:
Наиб.
общим делителем чисел a
и b,
Два способа нахождения НОД:
Описание алгоритма нахождения НОД делением:
Пример: Найти НОД для 30 и 18. 30/18 = 1 (остаток 12) 18/12 = 1 (остаток 6) 12/6 = 2 (остаток 0). Конец: НОД – это делитель. НОД (30, 18) = 6 Описание алгоритма нахождения НОД вычитанием:
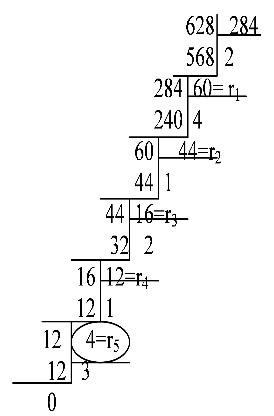
Пример: Найти НОД для 30 и 18. 30 - 18 = 12 18 - 12 = 6 12 - 6 = 6 6 – 6 = 0 Конец: НОД – это уменьшаемое или вычитаемое. НОД (30, 18) = 6 2) Алгоритм Евклида Пример: 628 и 284 (628, 284)=4 НОК
О Опр НОК чисел а и b наз-ют такое положительное целое число, которое делится на а и b и делит любое общее кратное Обознач:m=[a,b] если m- НОК, го: 1) m>0
2)
m
3)M
|
2.Поле комплексных чисел. Числовое поле. Геометрическое представление комплексных чисел и операций над ними. N € Z € Q € R € C из истор. Возник-я м-в. Рассотрим мн-во всевозможных пар действительных чисел: С={(а,в),а,в € R } изображается виде точек на плоскости. Определим отношение равенства и операций «+» и «*» 1. (а,в)=(с,д) ↔а=с,в=д. 2. (а,в)+(с,д)=(а+с,в+д) 3. (а,в)*(с,д)=(ас-вд,ад+вс) Опр: Мн-вом компл чисел наз мн-во всевозм пар действ чисел на к-ом опред опер-ции сложения и ум-ия по правилам 2,3.Элементы этого мн-ва называются комп чмслами. Обозначается: С=<{(а,в),а,в € R },+,*> Роль нулевого Эл – пара (0,0): -(а,в)=(-а,-в). Теорема: Мн-во ком чисел С=<{(а,в),а,в € R },+,*> образуют поле. Д-во (Тимофеенко): Д-во сводиться к проверке выполнимости св-в, определяющих поле 1) <C,+>- абелева (коммутат) гр→ из того что сложение пар сводиться к сложению их компонент, т.е. к слож дейст чисел, а дейст числа отн сложения обр-ют абелеву гр. 2) С*= <C\{0,0},*>- комм. гр. Для д-ва этого покажем : 2.1) что С* отн «*» замкнуто, т.е.: для (а,в) ≠0, (с,д)≠0 из С*→(а,в)(с,д) ≠0. (а,в) ≠0↔а≠0,в≠0 (с,д) ≠0↔ с≠0,д≠0. (а,в)(с,д)=(ас-вд, ад+вс) Могут ли однов-но ас-вд=0 и ад+вс=0? Проверим: ас-вд=0│*д -
-вд 2– вс2 =0│*(-1)
в(д 2 + с2 )=о -уже в R, значит в поле, тогда имеем: в=0 или (д 2 + с2 )=0 1) если в=0, то ас=0, с ≠0, а=0. 2) если (д 2 + с2 )=0, то д=о и с=0 – противоречие с усл, зн-т <C*,*> замкнуто. 2.2) что вып-ся условие может быть коммут. группой. Пусть q=(а,в), s=(c,д),k=(m,n). 1.qs=sq коммут 2. q(sk)=(qs)k ассоц 3. сущ е=(1,0) из С* для люб. q из С*: еq=q 4. люб. q из С* сущ s из С*: qs=е Теор.д-на. Теорема: В <С,+,*> разрешимо ур-ие (х,у)2 +(1,0)=(0,0). (х,у) 2+(1,0)=(х,у)(х,у)+(1,0)= =(х 2 - у2+1, 2ху)=(0,0). Сис-ма: х 2 - у2+1, 2ху=0, 2ху=0, Реш этой с-мы (0,1)=i- мнимая ед. Теорема: Мн-во дейст чисел изоморфно вкладывается в поле компл чисел, т.е. в поле С сущ подполе Д, к-е изоморфно полю <R,+,*>. Представление комплексных чисел Алгебраическая форма
Опр.
Запись комплексного числа
Сумма
и произведение комплексных чисел
могут быть вычислены непосредственным
суммированием и перемножением таких
выражений, как обычно раскрывая скобки
и приводя подобные, чтобы представить
результат тоже в стандартной форме
(при этом надо учесть, что
Сопряж.комп.числа:
Свойства:
1.Если
а
из
R,
то
2.
#
3.
Умнож-е аналогично сумме. 4.
6.
#
7.
f(x)-мн-н
с действ.коэф-тами и мнимое число
Тригонометрическая и показательная формы
Если
вещественную
Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:
Отсюда вытекают следующие широко используемые равенства:
Пример:
Формула Муавра . Для вычисления степени комп.числа задан.тригоном.формой применяется формула Муавра:
|

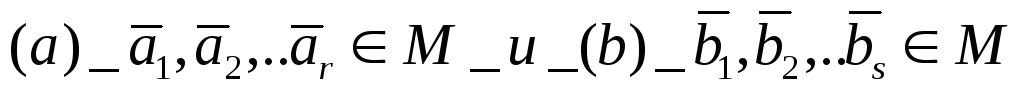 ,М-система n-мерн.векторов.
,М-система n-мерн.векторов.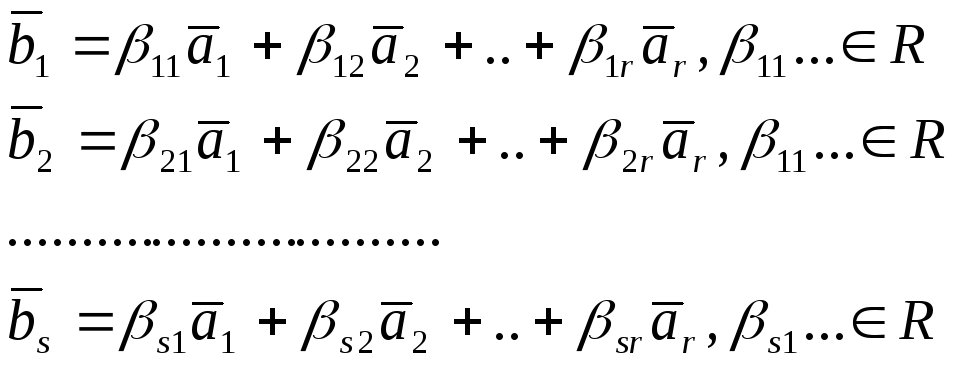
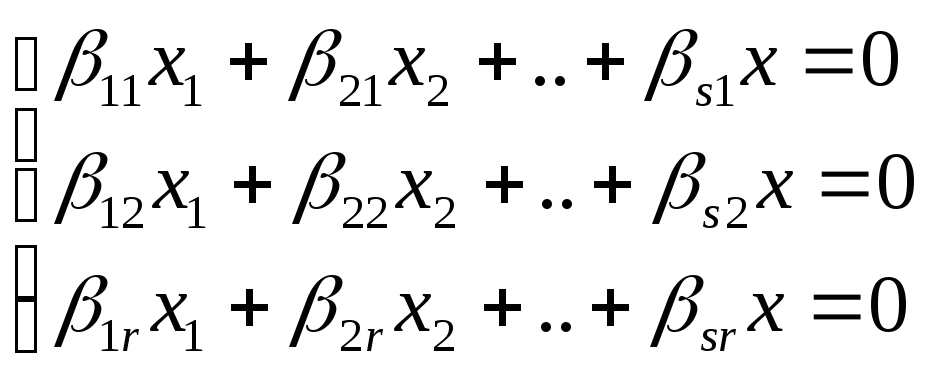 ОСЛУ,
в кот-й число ур-ний (r)
<числа неизвестных (s),
т.к. r<s,
такая сист.имеет и не нулев.решение.
Т.е.
ОСЛУ,
в кот-й число ур-ний (r)
<числа неизвестных (s),
т.к. r<s,
такая сист.имеет и не нулев.решение.
Т.е.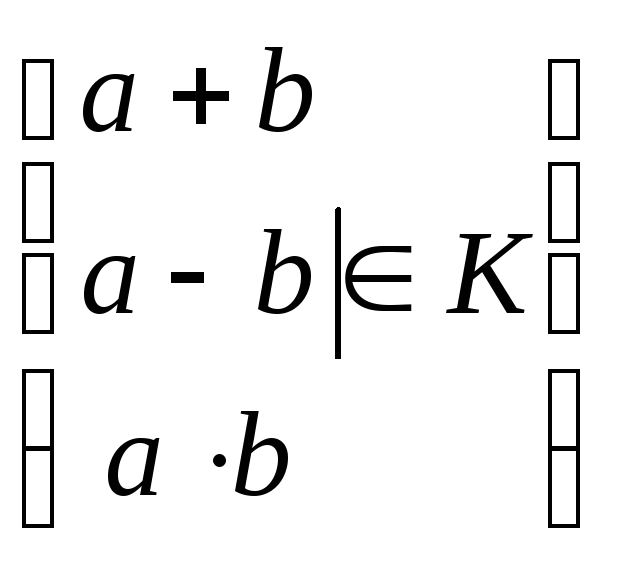 )
) пр
m-общее
кратное а и b, если m
пр
m-общее
кратное а и b, если m ад+вс=0│*с
ад+вс=0│*с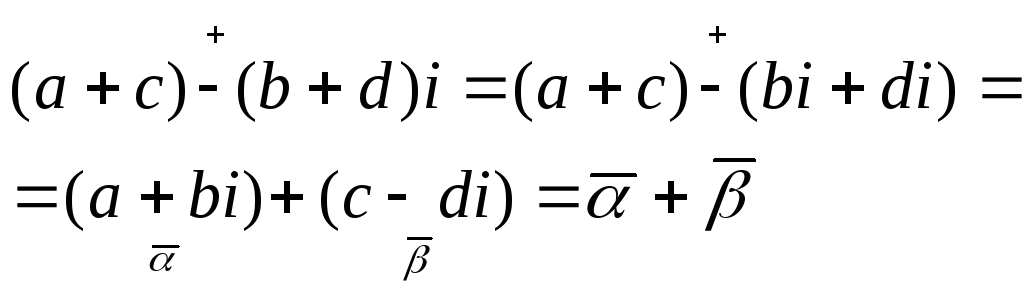 #
#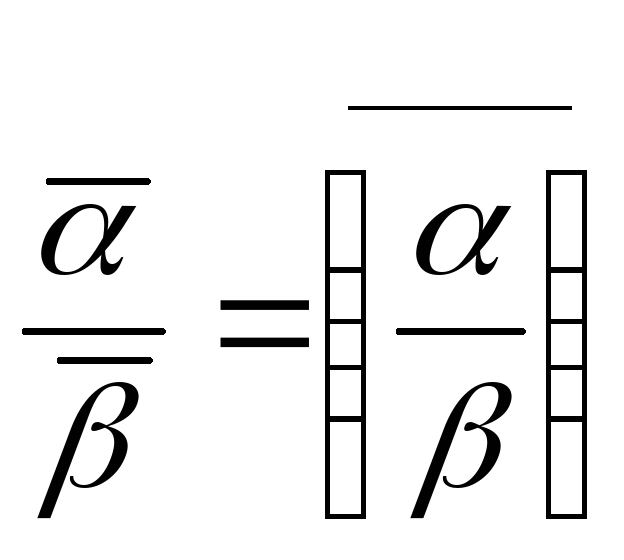
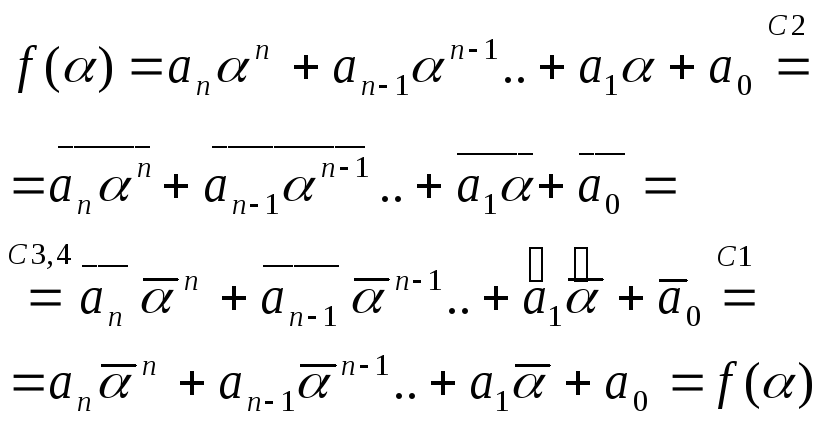 #
#