Многоэлектронный атом

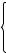
1

МНОГОЭЛЕКТРОННЫЙ АТОМ (конспект лекций)

1.Принципы квантовой механики

Квантовая химия атомов, молекул, молекулярных ансамблей и кристаллов опирается на следующие постулаты квантовой механики:

1. Каждое состояние системы n частиц полностью описывается функцией координат частиц xi и времени t

Ψ(x1, x2, …, xn, t) ≡ Ψ({x},t), называемой волновой функцией. Волновая функция существует во всем интервале изменения переменных; она непрерывна, конечна и однозначна. Выражение Ψ*({x},t)Ψ ({x},t)dx имеет смысл вероятности того, что в момент времени t i-я частица находится в интервале координат от xi до xi+dxi. Если справедливо выражение

∞∫Ψ* ({x}, t)Ψ({x}, t)dx1dx2 ,...,dxn =1,	(1)
-∞

то говорят, что волновые функции нормированы на единицу. Поскольку физический смысл имеет лишь плот-

ность вероятности Ψ*Ψ, то волновая функция определена с точностью до произвольного фазового множителя типа eiα. Ψ* - функция комплексно сопряженная с Ψ.

2. Каждой доступной измерению величине А в любом из возможных состояний соответствует линейный эрмитов оператор А. Оператор обозначается символом, определяющим математическую операцию, с помощью которой из одной функции получается друга. В квантовой химии используются операторы, которым отвечает уравнение типа

Аf = af,

(2)

где а − в общем случае комплексное число, называемое собственным значением оператора А; f называется собственной функцией оператора А.

Оператор, обладающий свойством
∫ f1* (x)Af2 (x)dx = ∫ f2 (x)A* f1* (x)dx	(3)

называется эрмитовым; собственные значения эрмитовых операторов − действительные числа, а их собственные функции образуют полный ортонормированный набор, т.е.

*	(x)fj (x)dx =δij	=	1, если i = j	(4)
∫fi			0, если i ≠ j.
А * – оператор, комплексно сопряженный с А;		δij – символ Кронекера.

Действуя на волновую функцию, оператор превращает ее в другую волновую функцию. Иными словами, действие оператора переводит систему в другое состояние; в частном случае система может остаться в том же состоянии.

Таблица 1

Операторы основных физических величин

	Переменная	Обозначение	Обозначение	Производимая
		переменной	оператора	операция

2

Координата

r

r

Умножение на r

∂

∂

∂

Момент

p

p

− i=

∂x

+

∂y

+

∂z

Кинетическая

=2

∂2

∂2

∂2

энергия

T

T

−

2

+

2

+

2

2m

∂x

∂y

∂z

Потенциальная

V(r)

V(r)

Умножение на V(r)

энергия

Полная

=2

∂2

∂2

∂2

E

H

−

+

+

+ V(r)

энергия

2

2

2

2m

∂x

∂y

∂z

Между операторами квантовой механики сохраняются те же соответствия, какие имеют место в классической механике между динамическими переменными (координата, импульс, энергия и т.д.): это утверждение состав-

ляет принцип соответствия.

3. Независящая от времени волновая функция удовлетворяет стационарному уравнению Шредингера:

HΨ = ЕΨ.	(5)
Эрмитов оператор полной энергии системы (гамильтониан)	H=T+V есть сумма оператора кинетиче-

ской энергии всех частиц системы Т и оператора их потенциальной энергии V; Е − полная энергия системы. Атомы, молекулы и кристаллы состоят из положительных ядер и отрицательных электронов, потенциальная энергия которых определяется кулоновским взаимодействием. Операторы кинетической энергии системы, со-

держащей М ядер, TЯ (R) и N электронов TЭ(r) выглядят следующим образом:

2

M

TЯ (R) = −

=

∑

1

a2 ,

(6)

2

a

Ma

=

2

N

TЭ(r) = −

∑ i2 ,

(7)

2m

i

где Ma − масса ядра a; m − масса электрона; 2 =

∂2

+

∂2

+

∂2

− оператор Лапласа (лапласиан), ħ =

∂x2

∂y2

∂z2

h/2π = 1,0545·10-34 Дж·с, где h – постоянная Планка.

Дифференцирование в уравнении (6) ведется по координатам ядер Ra , а в (7) − по координатам элек-

тронов ri.

Вид операторов потенциальной энергии (в системе СИ) следующий:

3

M

M

2

VЯЯ(R) = ∑∑

Za Zbe

, a ≠ b,

(8)

a

b 4πε0Rab

M

N

Zae

2

VЭЯ(R,r) = −∑∑

,

(9)

4πε0r

a

i

ai

N

N

e

2

VЭЭ(r) = ∑∑

, i ≠ j

,

(10)

i

j

4πε0rij

где Za и Zb − атомный номер элемента, e − заряд электрона, Rab − расстояние между ядрами, rai − рас-

стояние между ядром а и электроном i, rij − расстояние между электронами i и j, ε0 − диэлектрическая прони-

цаемость вакуума. Оператор (8) описывает отталкивание ядер, (9) − притяжение электронов к ядрам, (10) − отталкивание электронов.

Строго говоря, в гамильтониане следует учесть релятивистские эффекты, обусловленные близкой к световой скоростью движения электронов в низкоэнергетических состояниях (электронов остова), спинорбитальным взаимодействием и малыми флуктуациями движущихся электронов относительно средних позиций. Однако в хорошем приближении их можно игнорировать при рассмотрении многих квантовохимических задач.

Зависящая от времени волновая функция удовлетворяет нестационарному уравнению Шредингера

HΨ = i=	∂Ψ
	∂t ,	(11)

4.Все одинаковые частицы тождественны. Именно поэтому можно говорить о неразличимости электронов: замена одного из них другим не может быть обнаружена экспериментально.

5.Значения величины А, которые могут быть измерены, являются собственными значениями аi уравнения на собственные значения

АΨi = аiΨi ,

(12)

где собственные функции Ψi есть волновые функции, описывающие возможные состояния системы, в которых проводятся измерения. Это означает, что решение уравнения Шредингера (5) есть не что иное, как решение задачи на собственные значения для оператора полной энергии системы Н. Набор (спектр) собственных значений

Еi и набор собственных функций Ψi гамильтониана полностью характеризуют систему

HΨi = EiΨi , E0 ≤ E1 ≤ E2 ≤... ≤ En .

(13)

6. Среднее значение величины А для системы, находящейся в состоянии i, определяется выражением

ai = ∫Ψ*i (x)AΨi (x)dx

(14)

(предполагается, что волновые функции Ψ*i (x) ортонормированы). Если же система находится в нескольких состояниях, то

a = ∑Wi ∫Ψ*i (x)AΨi (x)dx ,	(15)
i

4

где Wi − вероятность пребывания системы в состоянии i, причем ∑Wi =1.

i
Соотношение (15), выражающее принцип суперпозиции состояний. Определение измеряемых характери-
стик системы с помощью волновых функций производится с использованием выражений (14) и (15).
7. Координату и импульс частицы в любом состоянии одновременно определить точно невозможно
(принцип неопределенности). Количественно этот принцип записывается следующим образом:
px x≥ ħ,	(16)
где px – проекция импульса частицы на ось х, обозначает неопределенность значений величины.

2.Вариационный принцип. Решение уравнения Шредингера

Согласно принципам квантовой механики для изучения электронных свойств химических систем необходимо решить уравнение Шредингера для всех возможных электронных состояний. Любая система стремится занять состояние с минимальной энергией. Поэтому решения ищут с помощью вариационного принципа, минимизируя энергию системы и определяя функции, максимально близкие к собственным функциям оператора Н. Вариационный принцип утверждает, что среднее значение энергии Еi любого из возможных i состояний системы, вычисленное с приближенной волновой функцией, не может быть меньше нижнего собственного значения Е0 оператора Н. Покажем это.

Среднее значение оператора Н для некоторой приближенной волновой функции Ψ, нормированной на 1,

равно

E = ∫Ψ* (x)HΨ(x)dx ≡ Ψ| H | Ψ .

(17)

которое сокращенно записывается как E =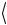Ψ| H | Ψ . Представим Ψ в виде разложения по собственным

функциям оператора Н:

					n
	Ψ = ∑ciΨi .										(18)
					i
Это всегда возможно, поскольку функции Ψi составляют полную ортонормированную систему. В силу
этого
							n			∫Ψi*Ψidx =1,
	∫Ψ*(x)Ψ(x)dx = ∑c*i ci										(19)
							i
откуда следует:
	n				n
	∑c*i ci =∑						ci		2 =1.		(20)
	i				i
Подставляя (20) в (19), имеем:
	n
E = ∫	Ψ* (x)HΨ(x)dx = ∑		ci		2 ∫Ψ*i (x)HΨi (x)dx ,						(21)

i

5

где Еi − энергия i-го состояния. С другой стороны,

n				2Ei ,
E = ∑		ci							(22)
i
откуда
		n						2 = E0 ,
E ≥ E0 ∑						ci			(23)

i

где Е0 − нижнее (наименьшее) собственное значение оператора Н, так как энергии возбужденных состояний выше, чем энергия самого низкого по энергии состояния, называемого основным. Что и требовалось доказать.

Итак, чтобы решить уравнение Шредингера, нужно минимизировать выражение для энергии (17), т.е.

подобрать такие волновые функции, для которых энергия будет минимальна. Это можно сделать, если волновая функция включает некоторые переменные параметры, изменяя которые можно обеспечить минимум. Напри- мер, принцип суперпозиции позволяет записать волновую функцию в виде линейной комбинации

n
Ψ = ∑ciϕi ,	(24)

i

где ϕi − n выбранных из некоторых соображений функций, часто называемых базисными (например, для атомов

− это могут быть атомные орбитали, которые мы рассмотрим далее), ci − переменные комплексные параметры. Чтобы найти минимум энергии (17), нужно, чтобы все первые производные энергии по параметрам ci равнялись нулю, а вторые производные были положительны. Однако обычно ограничиваются равенством нулю

первых производных, что отвечает условию стационарности энергии:

	∂Ε	=		∂Ε	= ... =		∂Ε		= 0 ,
	∂c1			∂c2			∂cn
									(25)
	∂Ε			∂Ε			∂Ε
		=			= ... =				= 0
	∂c*			∂c*		∂c*
	1			2			n

На языке вариационного исчисления, обычно используемого в квантовой химии, условие (25) эквивалентно требованию обращения в нуль первой вариации (вариация – бесконечно малое изменение функции):

δ∫Ψ* (x)HΨ(x)dx = 0 .

(26)

Из условия стационарности (25) должен следовать набор уравнений, решая которые совместно, можно найти параметры ci . При этом следует принять во внимание, что параметры ci не независимы, а связаны в силу ортономированности функции Ψ соотношением:

∫Ψ	*	n	n	*	*	n	n	*	(27)
		(x)Ψ(x)dx = ∑∑ci c j ∫ϕi				(x)ϕj(x)dx = ∑∑ci c jSij =1.			(27)
		i	j			i	j

6

Интеграл Sij = ∫ϕ*i (x)ϕj(x)dx называется интегралом перекрывания функций ϕi и ϕj.

При минимизации с учетом ограничений, каковым является условие (25), в математике используется метод неопределенных множителей Лагранжа. Вводя такой множитель Е, представим уравнение для определения параметров ci в виде:

δ [ ∫Ψ* (x)HΨ(x)dx −E(∑∑ ∫ϕi* (x)ϕj (x)dx −1) ]=

i j

=δ [	n	n	(28)
	∑∑c*i cj ∫ϕi* (x)Hϕj (x)dx −E(Sij −1)		]= 0 .
	i	j

Теперь все параметры ci можно считать независимыми. Производя варьирование по ci и cj, имеем в компактной записи:

n

n

∑дс*i

∑сj [Hij − ESij ] = 0,

i =1,2,3,..., n

(29)

i

j

n

n

∑дсj ∑с*i [Hij −ESij ] = 0,

i =1,2,3,...,n

j

i

где Hij = ∫ ϕ*i (x)Hϕi (x)dx − матричные элементы оператора Н в базисе функций ϕi

(x) , Sij −

элементы матрицы интегралов перекрывания, вычисленной с тем же набором функций ϕi

(x):

H

11

H

12

.....

H

1n

S

S

.....

S

11

12

1n

H =

H21

H22

.....

H2n

S = S21

S22

.....

S2n

(30)

.....

.....

.....

.....

,

..... .....

.....

.....

Hn2

.....

Sn2

.....

Hn1

Hnn

Sn1

Snn

Поскольку все вариации δсi в (29) независимы, матричные уравнения справедливы лишь, если коэффициенты при вариациях равны нулю. Каждое матричное уравнение в (29) получается из другого операцией комплексного сопряжения, поэтому достаточно рассматривать только одно из них:

n
∑сj [Hij −ESij ] = 0,	i =1,2,3,...,n	(31)

j

7

Полученная система однородных линейных уравнений позволяет найти параметры ci, обеспечивающие минимум функционала (17). Чтобы ее решить, необходимо приравнять нулю определитель (детерминант) из коэффициентов при ci:

	H11	− ES11	H12	− ES12			.....	H1n	− ES1n
	H 21	− ES21	H 22	− ES22			.....	H 2n	− ES2n	= 0	(32)
		.....		.....			.....		.....
	H n1	− ESn1	H n 2	− ESn2			.....	H nn	− ESnn
или в других обозначениях
			Hij − ESij			= 0					(33)

Уравнение (33) впервые возникло в задачах классической механики о вековых (секулярных) возмущени-

ях планетарных орбит. Отсюда его название − вековое или секулярное уравнение. При разложении определителя получается многочлен n-й степени по Е, значит, вековое уравнение имеет n корней − n различных значений Е. Подставляя их в (31), можно найти набор параметров ci . Величины Еi играют роль энергий состояний системы.

Чтобы найти волновую функцию основного состояния, нужно взять наименьшее из полученных значе-

ний энергии и, подставив его в (31), найти коэффициенты сi, а затем и волновую функцию Ψ по формуле (24). Волновые функции возбужденных состояний ищут аналогичным образом, учитывая, что они должны быть ортогональны друг другу.

Точное решение уравнения Шредингера возможно только для атома водорода и водородоподобных ионов. Для многоэлектронных атомов необходимо применять приближения, рассмотренные ниже.

3.Приближение независимых частиц. Одноэлектронная модель

Рассмотрим, как можно найти волновые функции и уровни энергии неподвижного N-электронного ато-

ма, максимально близкие к точным. Выберем начало координат на его ядре с зарядом Z e . Гамильтониан в

этом случае имеет вид:

(34)

2		N	N	Ze	2			N	N	2
H = Tэ(r) + Vэя (r, R) + Vээ(r) = −	=	∑ i2 −∑					+ 12	∑∑		e
	2m			4πε	0	r				4πε	r
		i	i			i		i	j	0	ij

Вначале просто исключим из (34) оператор энергии межэлектронного взаимодействия Vээ. Многоэлектронное уравнение Шредингера в этом случае распадается на систему из N одноэлектронных уравнений

hi χi (ri ) =εi χi (ri )								i =1,2,3,...,N	(35)
c одноэлектронными гамильтонианами
h		= −	=2	2	−	Ze2		.	(36)
			2m			4πε	r
	i			i
						0	i

		и имеет энергию ε		8
Согласно (35) электрон i описывается волновой функцией χ	(r )		i	. Это означает,
i	i

что поведение каждого электрона не зависит от поведения остальных электронов и описывается некоторой волновой функцией подобно единственному электрону в атоме водорода. В этом состоит суть приближения неза-

висимых частиц. Решения одноэлектронных уравнений (35) χi (ri ) называются одноэлектронными волновыми функциями или орбиталями (в атоме − атомными орбиталями, в молекуле − молекулярными, в кристалле − кристаллическими).

Полный гамильтониан атома в этом приближении есть просто сумма одноэлектронных гамильтонианов:

				N
				H = ∑hi .	(37)
1
Собственные функции Н представляют собой произведение атомных орбиталей, заселенных электрона-
ми:
Ψ=χ1(r1) χ1(r2 ) χ3(r3) χN (rN ) ,					(38)
а энергия атома является суммой индивидуальных орбитальных энергий:
Ψ		H		Ψ = ε1 +ε2 +ε3 +...+εN = E.	(39)

Приближенная волновая функция вида (38) называется волновой функцией Хартри.

Гамильтониан (36) является чрезмерно упрощенным: энергия электрон-электронного отталкивания не мала и пренебрегать ею нельзя.

4.Метод самосогласованного поля

Более близкие к истинным решения получают с помощью метода самосогласованного поля (ССП), предложенного Хартри. В методе ССП межэлектронным отталкиванием не пренебрегают, но действие на данный электрон всех остальных электронов заменяют средним полем, приближенно воспроизводящим их суммарное действие; последнее зависит от координат только рассматриваемого электрона. Это дает возможность разделить в сферической системе координат переменные в уравнении Шредингера. С формальной точки зрения это достигается следующим образом. Одноэлектронный гамильтониан записывают в виде:

ССП

=

2

2

Ze

2

N

e

2

= −

−

+ ∑

, j =1,2,3,...,(N -1)

(40)

hi

2m

i

4πε

r

4πε

r

0 i

j

0 ij

j

Последнее слагаемое описывает отталкивание между электронами i и j, усредненное по всем положениям электрона j и, следовательно, зависящее только от координат электрона i . Последствия этого состоят в следующем.

Рассмотрим гамильтониан

n
Н= ∑hССПi	.	(41)
i
Его собственные функции (функции Хартри) имеют вид орбитальных произведений:
Ψ=χ1(r1) χ1(r2 ) χ3(r3 ) χN (rN ) .		(42)

9

Собственные значения Н представляются суммой собственных значений hССПi :

.

n	n
E' = ∑еi =∑ Ψ | hССПi | Ψ		(43)
i	i

Энергия εi есть сумма кинетической энергии i-го электрона, потенциальной энергии его притяжения к ядру и средней потенциальной энергии его отталкивания от остальных электронов. Следовательно, Е′ естьсумма кинетической энергии всех электронов, потенциальной энергии их притяжения к ядру и удвоенной потенциальной энергии их усредненного отталкивания от остальных электронов. Удвоение возникло потому, что оттал-

кивание между электронами i и j учтено дважды: как среднее по j в hССПi							(40) и среднее по i в hССПj . С уче-
том этого, полная энергия атома равна:
1	n	n		e2			i ≠ j.	(44)
E = E'− 2	∑∑			4πε r
	i	j		0	ij i, j

Соответственно, гамильтониан атома должен иметь вид:

H = H −	1	n	n		e2			,	i ≠ j .	(45)
	2	∑∑			4πε r
		i	j		0	ij		i, j

Таким образом, необходимо решить систему одноэлектронных уравнений с гамильтонианом (45), включающим усредненное межэлектронное взаимодействие – систему уравнений Хартри. Для этого нужно постро-

ССП	, для чего следует прежде рассчитать усредненные величины		e	2				. Как
ить набор операторов hi
			4πε		0	r		j
						ij

это сделать? Вероятность того, что электрон j с волновой функцией χj(rj) находится в бесконечно малом объеме dvj, равна χ2j dv j (рис. 1).

Рис. 1. Иллюстрация к вычислению усредненного межэлектронного кулоновского взаимодействия. Электрон i в

точке, последовательно “пробегающей” все положения в пространстве Значит, отталкивание электрона i, усредненное по всем положениям

электрона j, равно:

e2

= e

2

∞

χj 2 (rj )

dv

.

(46)

4πε

r

4πε

r

0

j

∫

0

j

ij

−∞

ij

Однако, чтобы вычислить этот интеграл, волновые функции

χj (rj ) должны уже быть известны! Это

противоречие преодолевается следующим образом. Сначала задаются некоторым набором N одноэлектронных

10

функций, максимально близких к правильным χ0j (rj ) (позже мы увидим, что сделать это легко). С их по-

мощью вычисляют интеграл (46) и строят оператор (h0i )ССП . Затем решают набор одноэлектронных урав-

нений Хартри, возникающий из условия минимума среднего значения гамильтониана (40), вычисляемого с волновой функцией Хартри (42):

=

2

2

Ze

2

2

N

∞

0

2

1

1

∑

∫

[χj

(rj )]

−

i

−

+e

dv j

χi

(ri ) = εi χi

(ri ), i =1,2,3,...,N .

(47)

2m

4πε

r

j ≠i

4πε r

o

i

−∞

o ij

Полученные решения χ1 (r ) используют, чтобы построить "исправленный" оператор (h1 )ССП

, вновь

i

i

i

решают ту же систему уравнений, но теперь – с (h1i )ССП и т.д. – до тех пор, пока получаемые собственные значения уравнений Хартри (т.е. энергии состояний) будут отличаться от полученных на предыдущей итерации лишь на очень незначительную величину (~ 10-6 а.е.). Этот процесс называется самосогласованием, а результи-

рующее поле, создающее усредненный потенциал в (40), называется самосогласованным полем – отсюда и на-

звание метода. Отметим, что сходимость метода не гарантируется теорией, но, как правило, достигается на

практике. Существуют довольно хорошо разработанные методы, которые позволяют обойти встречающиеся

здесь иногда затруднения.

Одноэлектронное приближение и метод ССП на первый взгляд кажутся довольно грубыми, однако это не так. Дело в том, что быстро движущийся электрон “чувствует” скорее среднее эффективное поле остальных частиц, чем реагирует на мгновенные изменения их позиций. Принципиально важно, что самосогласованные решения удовлетворяют вариационному принципу, т.е. приводят к средним значениям энергии состояний, которые не ниже, чем точные энергии.

5. Приближение центрального поля

N		e2
Потенциал ∑						в (40) только в частных случаях (положительные одноэлектронные ио-
		4πε		r
j			0	ij		j

ны, атомы инертных газов, атомы N, P и т.д.) является сферически симметричным, т.е. не зависит от углов θ и ϕ в сферической системе координат. Опыт, однако, показывает, что учет асферичности электронного распределения не улучшает заметно результат расчета. Поэтому обычно используют дополнительно усредненный по всем направлениям потенциал в (40), интегрируя его по углам θ и ϕ:

N

e2

e2

π 2π

χj 2 (rj )

2

=

r

sinθ

dθ

dϕ dr

. (48)

∑j

4πε

r

4π ∑i

4πε

r

0

∫ ∫

0

j

j

j

j j

ij j,θ,ϕ

0 0

ij

Вводимое таким образом приближение центрального поля имеет весьма важные последствия: оно позволяет рассматривать ССП-решения для любого атома как модифицированные решения для одноэлектронного