Lektsia_3_4_Atom_H

2э = ∂∂x22 + ∂∂y22 + ∂∂z22

1

Пример: Атом водорода в сферической системе координат

Рассмотрим, как можно получить волновые функции, описывающие состояния атома водорода и рассчитать уровни его энергии. Атом водорода состоит из отрицательно заряженного электрона и ядра, несущего положительный заряд. Оператор Гамильтона, описывающий энергетические состояния атома водорода, имеет вид

	Н = −	=2	2	−	=2	2	+ V(r).	1(1.108)
		2M			2m
			Я			э

Индексы «Я» и «э» относятся к ядру и электрону, соответственно, М и m –массы ядра и электрона, =– постоянная Планка. Оператор Лапласа (лапласиан) в (1) имеет вид в декартовой

системе координат . Дифференцирование ведется по координатам электронов

ri. Потенциальная энергия взаимодействия электрона и ядра зависит только от расстояния между ними r и описывается законом Кулона

V(r) = −	1		Ze2	=−	1		Ze2
			r					,	(2)
	4πεO				4πεO
							x2 + y2 + z2

где ε0 – электрическая постоянная, е – заряд электрона, Z – атомный номер (для атома водорода Z=1). При бесконечном удалении частиц энергия их кулоновского взаимодействия равна нулю. Декартовы переменные в знаменателе не разделяются.

В отсутствие внешних сил атом водорода как целое движется с постоянным импульсом. Поэтому можно отделить поступательное движение атома от других видов движения, поместив начало системы координат в центр масс. Тогда уравнение Шредингера, включающее «внутреннюю» энергию атома Е (энергию, не учитывающую поступательное движение системы) прини-

	мает вид
			{ −	=2	2 +V(r)} Ψ(r) = Е Ψ(r)	(3)
				2μ
					э
	Формально задача сводится к описанию движения отрицательно заряженной частицы с
	приведенной массой μ =	mM	относительно центра масс 1. Положение центра масс практи-
		m + M

чески совпадает с положением ядра, а размеры ядра во много раз меньше расстояния до электрона. Поэтому ядро можно считать точечным, создаваемое им электростатическое поле центральным, а движение в атоме водорода рассматривать как движение электрона в поле ядра.

1 Масса протона примерно в 1836 раз больше массы электрона. Это означает, что приведенная масса атома водорода составляет μ≈0.9995m, то есть несущественно отличается от массы электрона.

2

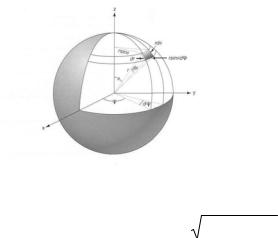
Совместим начало координат с положением ядра и перейдем от декартовых коор-

динат x, y, z к сферическим координатам r, θ, ϕ (0 ≤ r ≤∞, 0 ≤ θ ≤ π, 0 ≤ ϕ ≤ 2π). Связь между координатами точки, в которую направлен радиус-вектор r, в разных системах иллюстрирует рис-к.

Математически эта связь описывается следующим образом:

x = r sinθcosϕ, y= r sinθsinϕ, z = r cosθ; r = x2 + y2 + z2 ,

(4)

Оператор Лапласа в сферических координатах имеет вид

2

1

∂

2

∂

1 ∂

∂

1 ∂2

r,θ,ϕ

=

r

+

sinθ

+

.

(5)

r2

sin2 θ ∂ϕ2

∂r

∂r

sinθ ∂θ

∂θ

Соответственно, уравнение Шредингера для атома водорода в сферических координатах записывается как

1

∂

r2

∂

+

1

∂

sinθ

∂

+

1

∂

2

Ψ(r,θ,ϕ) +

2

r

2

r

2

sin

2

θ ∂ϕ

2

r

∂ r

∂ r

sinθ ∂θ

∂θ

+

2μ

[E −V (r)]Ψ(r,θ,ϕ) = 0

(6)

=2

Домножим обе части уравнения (6) на r2 и сгруппируем члены, отдельно - зависящие только от расстояния r и отдельно - от углов θ и ϕ:

∂

2 ∂

2 2μ

1

∂

∂

1 ∂

2

r

+r

[E −V (r)]

+

sinθ

+

Ψ(r,θ,ϕ) =0

(7)

2

2

2

=

sin

sin

θ ∂ϕ

∂r

∂r

θ ∂θ

∂θ

Можно считать, что оператор, действующий на волновую функцию в выражении (7), есть сум-

ма двух операторов, каждый их которых действует на «свои» переменные – r и (θ, ϕ). В этом случае в сферических координатах волновую функцию Ψ(r,θ,ϕ) можно представить в виде про-

изведения двух независимых друг от друга функций, одна из которых R (r) зависит только от

3

расстояния до электрона r , а другая Y(θ, ϕ) - от углов θ и ϕ: Ψ(r,θ, ϕ) = R (r)Y(θ, ϕ). Это по-

зволяет разделить уравнение (7) на две части - радиальную

∂			2	∂			2 2μ		[E −V (r)]
		r				+r	=	2		R (r) =λ R (r)
	∂r			∂r

и угловую

1

∂

∂

1

∂ 2

sinθ

+

+λ Y (θ,ϕ) =0.

sin

2

θ ∂ϕ

2

sin

θ ∂θ

∂θ

(8)

(9)

Для этого нам пришлось ввести постоянную разделения λ.

Домножим далее (9) на sin2θ и представим угловую функцию в виде произведения

Y(θ,ϕ)=Θ(θ)Φ(ϕ). Тогда можно аналогичным образом разделить переменные θ и ϕ, получив два уравнения:

sinθ	∂		sinθ		∂		+(λ −m2 )sin2	θ		Θ(θ) = 0	(10)
	∂θ				∂θ
		∂ 2
				Ф(ϕ) +m2Ф(ϕ) = 0 .							(11)
		∂ϕ2

Здесь постоянная разделения обозначена как m2.

Таким образом, в сферических координатах представление волновой функции в виде произведения

Ψ(r θ ϕ) = R(r)Θ(θ)Φ(ϕ)

(12)

позволяет разбить уравнение Шредингера для атома водорода (6) на три уравнения, каждое из которых содержит один или два параметра. Решая эти уравнения по отдельности, можно найти эти параметры, получить волновую функцию и рассчитать возможные значения энергии атома водорода.

Решение уравнения (11) Φ(ϕ) ищут, учитывая стандартные условия, накладываемые на волновую функцию. Изменение угла ϕ может рассматриваться, как вращение электрона в плоскости, которое описывается уравнением бегущей волны Φm(ϕ) = a exp(imϕ). Достаточно ограничиться движением в одном направлении (противоположное движение описывается путем замены m на –m). Согласно условию однозначности волновой функции, один полный оборот приводит систему в исходное положение; следовательно, справедливо

4

Φ(ϕ)=Φ(ϕ+2π).

(13)

Отсюда следует, что exp(i2πmϕ) =1. Это требование выполняется, если

m=0, ±1, ±2, ± 3, …

(14)

Условие нормировки для волновой функции вида (12) выглядит следующим образом:

∞∫∫π 2∫π			|Ψ(r ,θ, ϕ)|2dxdydz = ∞∫	|R (r)|2r2 dr π∫	|Θ(θ)|2 sinθdθ	2∫π	|Φ(ϕ)| dϕ =1 (15)
0	0	0	0	0		0

(r2sinθdrdθdϕ - элемент объема в сферических координатах, соответствующий объему dxdydz в декартовых координатах). Условия нормировки для каждой из функций по отдельности следующие:

∞∫ |R (r)|2r2 dr =1

0

π∫	|Θ(θ)|2 sinθdθ =1				}	(16)
0
2∫π	|Φ(ϕ)|2 dϕ =1
0
Отсюда следует
2∫π (Φ(ϕ)(2 dϕ = a2				2∫π eimϕe−imϕdϕ = a2 2π =1 ,		(17)
0				0
что дает а2= (1/2π). В итоге, решение уравнения (11) имеет вид
Φ(ϕ)=		1	eimϕ ,		m=0, ±1, ±2, ±3,…	(18)
		2π

Теперь можно перейти к уравнению (10). Мы не станем входить здесь в детали процедуры его решения. Отметим лишь, что, если разделить (10) на sin2θ и потребовать, чтобы выполнялось условие λ=l(l+1), где l – целое неотрицательное число, причем l≥|m|, то уравнение (10) транс-

5

формируется в присоединенное уравнение Лежандра. Его решения Pl m (cos θ) называются при-

соединенными полиномами Лежандра и определяются соотношением

Pm (cos θ) = (−1)l	sinm θ		d l+m	sin2l θ .
	2l l!		(d cosθ)l+m
l

Здесь l!=1·2·3·…·(l-1)·l. Нормированные (см. (17) присоединенные полиномы Лежандра имеют вид

(1−

m

1

2

m

(2l +1)

)!

Pl

Plm(θ)=

(cos θ) ,

(19)

2

(1

+

m

)!

где l = 0, 1, 2,..; m = - l, ..0, …+ l. Несколько первых нормированных присоединенных полиномов Лежандра приведено в таблице:

Первые нормированные присоединенные полиномы Лежандра

l	m		Plm(θ)
0	0			1	2
				2
	0		1	6 cosθ
			2
1	±1		1	3 sinθ
			2
	0	1	10(3cos2 θ −1)
		4
2	±1	1	15 sinθ cosθ
		2
	±2		1	15 sin2 θ
			4

Теперь мы можем записать решение для угловой части уравнения Шредингера для атома водорода (9) следующим образом:

6

1

(2l +

1)

(1 −

m

)!

Ylm(θ, ϕ)=(−1)

(m+ m )/2

2

Pl

m

(cos θ)exp(imϕ). (20)

4π

(1 +

m

)!

Комплексные функции Ylm(θ,ϕ) называются сферическими гармониками. Эти функции не зави-

сят ни от вида центрального потенциала, ни от приведенной массы μ. Они являются четными при четных l (то есть, не меняют своего знака при изменении направления всех трех осей декартовых координат) и нечетными при нечетных l. При разных значениях l и одном и том же значении m функции Ylm(θ,ϕ) ортогональны друг другу. Множитель (−1)(m+ m )/2 отвечает стандартному выбору фазы сферической гармоники, введенному Кондоном и Шортли.

Для конкретного значения l имеется l поверхностей, проходящих через положение ядра,

где функции Ylm(θ,ϕ) обращаются в нуль; они называются узловыми поверхностями или просто узлами. Вероятность найти электрон в узле равна нулю. Таким образом, для каждого l имеются 2l+1 сферических гармоник, отличающихся положением в пространстве узловых поверхностей; квантовое число m определяет ориентацию узловых поверхностей.

Наличие узловых поверхностей у волновых функций атомов (и молекул) связано с волновыми свойствами электронов. В любой волне имеются точки, в которых смещение колеблющейся величины равно нулю; в случае, когда колебания происходят в трех измерениях, совокупность этих точек образует узловую поверхность.

Из-за комплексного характера функций Ylm(θ,ϕ), их графическое изображение при m≠0 весьма затруднительно. К счастью, можно перейти к действительным линейным комбинациям этих функций, которые уже легко изобразить в том или ином виде.

Вернемся теперь к полному уравнению Шредингера для атома водорода (6) и перепишем его следующим образом:

∂

2 ∂

2m

2

l(l +

1)

1

r

+

E −V (r) −

=

R (r) =0.

(21)

∂ r

∂ r

=2

2mr2

r2

Подставляя явное выражение для энергии кулоновского взаимодействия (2), получаем

∂

2

∂

2m

1

Ze

2

2

l(l +1)

1

=

r

+

E +

−

R (r) =0 .

(22)

2

=

2

4πε

r

2mr

2

r

∂ r

∂r

O

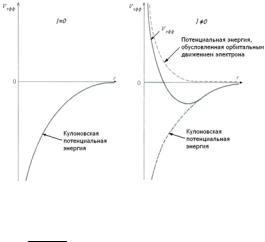
В этом выражении можно выделить эффективный потенциал

7

	V	(r) = −	1	Ze2	+	=2l(l +1)	,	(23)
			4πεO			2mr2
	эфф			r

в котором первый член обусловлен кулоновским притяжением электрона к ядру, а второй – орбитальным движением электрона, приводящим к центробежным силам, препятствующим “падению” электрона на ядро. Вид эффективного потенциала (23) показан на рис-ке.

При l =0 центральная сила F = − ∂V∂эффr , действующая на электрон, имеет притягивающий ха-

рактер. Учитывая волновые свойства электрона, можно утверждать, что в этом случае имеется ненулевая вероятность найти электрон в положении ядра. При l ≠0 вблизи ядра доминирует центробежная сила, и электрон не может находиться на ядре. Заметим, что этот важный вывод, к обсуждению которого мы еще вернемся, сделан до окончательного решения уравнения Шредингера.

Вид эффективного потенциала позволяет сделать еще один важный вывод. Поскольку потенциал (2) задан так, что на бесконечном расстоянии энергия кулоновского взаимодействия электрона и ядра равна нулю, движение связанного электрона в атоме происходит в области ограниченной некоторым значением r (классически траекторию движения связанного электрона можно представить как эллипс). Это означает, что, если энергия электрона Е отрицательна, существуют его связанные состояния. При Е>0 потенциальный барьер с ростом r не возникает, и движение электрона становится неограниченным. Начиная с некоторого значения l второй член в (23) доминирует настолько, что эффективный потенциал Vэфф становится положительным при любых r и связанные состояния возникнуть не могут. Это уместно сопоставить с уже отмечавшимся фактом, что с ростом l пространственное квантование вектора углового момента фактически не проявляется.

Собственные функции уравнения (9) для Е<0 и Е→0 при r →∞ выражаются через известные в математике обобщенные полиномы Лягерра:

8

k	(ξ )=	d k		ξ d z			z		−ξ		(24)
L			e			(ξ		e		)
					dξz
z		dξk

(ξ - греческая буква кси). Несколько первых обобщенных полиномов Лягерра приведены в таб-

лице:

Обобщенные полиномы Лягерра для n ≤3 и l≤2; ξ = 2Z r na0

Точный вид нормированной радиальной функции R n,l при k=2l+1, z=n+l и ξ = 2Zr

следующий:

na0

1/2

3

ξ

2Z

(n −l −1)!

l

2l+1

R n,l (ξ) = −

ξ

exp(−

)Ln+l (ξ).

(25)

3

2

na0

2n[(n +l)!]

Для атома водорода Z =1. Величина a 0

=

4πε0 =2

=0.529·10-10 м называется радиусом Бора. Не-

e2 m

которые радиальные функции атома водорода изображены на рис-ке ниже. Решения (25) существуют только в случае, если число n принимает целые положительные значения: n=1, 2, 3, …,

причем n≥l+1. Число n называется главным квантовым числом; n определяет собственные значения уравнения (9), то есть задает возможные значения энергии электрона в атоме водорода.

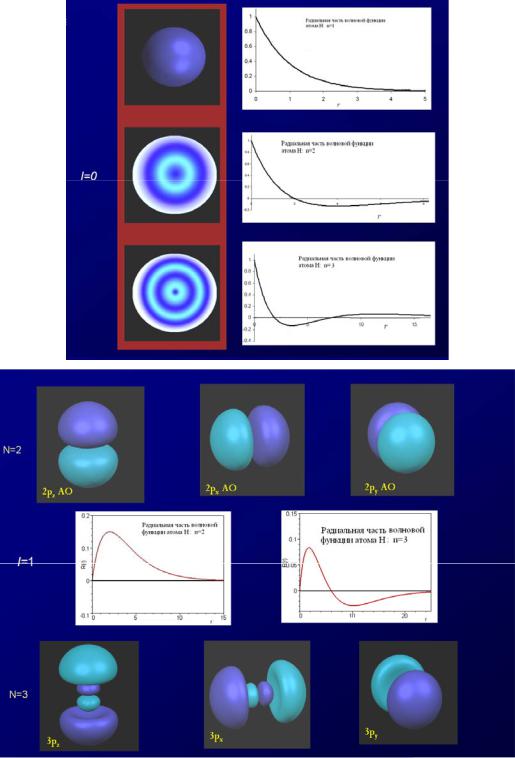
9

Эта энергия дается выражением

	E = −	Z 2e2	1	(26)
		2a	n2
	n
		0

10

(для атома водорода Z=1). Поскольку это выражение содержит целочисленные значения n, спектр разрешенных значений энергии стационарных состояний электрона в атоме водорода оказывается дискретным. Подчеркнем, что соотношение (26) не содержит явно квантовых чисел m и l.

Теперь, комбинируя выражения (25) и (20) и положив Z=1, мы получаем волновые функции атома водорода в виде

1/ 2

3

l

2

(n −l −1)!

2r

r

2r

Ψ(r, θ, ϕ) = −(−1)

(m+m )/2

2l+1

×

exp(−

)Ln+l

3

na0

na0

2n[(n +l]

na0

na0

1

× (2l +1) (1

−

m

)!

2

P

m

(cosθ) exp(imϕ).

(27)

4π

(1

+

m

l

)!

Эти функции являются собственными функциями уравнения Шредингера (16). Это комплексные функции, каждая из которых описывает некоторое электронное состояние атома, зависят от квантовых чисел n, m и l:

n = 1, 2, 3, …,
l=0, 1, 2, 3,…, n -1,	(28)
m = -l, -l+1, -l+2, …., 0, …. l -1, l

Состояния, зависящие от l или m, но имеющие одно и тоже значение n, имеют одинаковую энергию (26). Поэтому при n>1 одной и той же энергии атома соответствуют несколько возможных состояний с разными значениями l; в свою очередь, каждому из них соответствует 2l+1 состояний с разными значениями m. Такие состояния называются вырожденными. Полная кратность вырождения стационарного электронного состояния с главным квантовым числом n равна

n−1
∑(2l+1) = n2 .	(29)

l=0

Волновые функции атома водорода обозначаются с помощью смешанных буквенноцифровых символов:

l=0 → ns l=1 → np l=2 → nd l=3 → nf l=4 → ng l =5 → nh

(n – главное квантовое число). Кодировка s, p, d и f возникла в результате визуального наблюдения линий в спектрах атомов, которые позднее были связаны с волновыми функциями электронных состояний. Символ s (sharp) соотносилис яркими, четкими линиями, p (principal) – с основными наиболее интенсивными линиями, d (diffuse) – с размытыми линиями и f (fine) - с тонкими линиями. Далее буквы следуют согласно английскому алфавиту. Таким образом, в зависимости от комбинации n и l говорят о 1s, 2s, 2p, 3p, 3d, 4f функциях и т.д. Полные выраже-