
МАТАН / Перегиб
.doc18. Определение выпуклости и вогнутости графика функции. Достаточные условия.
График функции y=f(x) называется выпуклым [вогнутым] в точке (x0;f(x0)), если в этой точке существует касательная к этому графику, которая в некоторой окрестности этой точки расположена выше [ниже] этой кривой.
График функции y=f(x) называется выпуклым [вогнутым] на интервале (a;b), если он выпуклый [вогнутый] в каждой точке этого интервала.
Если функция y=f(x) дважды дифференцируема на интервале (a;b) и ее вторая производная отрицательна [положительна] во всех точках этого интервала, то график функции y=f(x) является выпуклым [вогнутым] на этом интервале.
19. Определение точки перегиба. Достаточные условия.
Точка (x0;f(x0)) называется точкой перегиба графика функции y =f (x), если в этой точке существует касательная и если она отделяет интервал выпуклости от интервала вогнутости.
Пусть функция y=f(x) дважды дифференцируема в некоторой окрестности точки x=x0, и в точке (x0;f(x0)) существует касательная к графику этой функции. Если при переходе через точку x=x0 вторая производная меняет знак, то точка (x0;f(x0)) является точкой перегиба графика функции.
20.Понятие о неопределённостях(дополнение смотреть в пределах). Правило Лопиталя
Функция …..при х →a представляет собой неопределённость типа ….. ,еслипредел дан ф-ии сравен нулю Раскрыть указанную неопределённость значит вычислить предел……., если он не существует .Функция не определена при х.
Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки x=x0 и
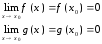
и
![]() , то выполняется равенство
, то выполняется равенство
![]()
21. Определение асимптоты к графику функции. Нахождение наклонной и вертикальной асимптоты.
Асимптотой данной кривой называется такая прямая, что расстояние от точки на кривой до этой прямой стремится к нулю при неограниченном удалении этой точки от начала координат.
Наклонные (невертикальные) асимптоты - асимптоты, не параллельные оси oy. Кривая, заданная уравнением y=f(x) имеет невертикальную асимптоту, определяемую уравненем y=kx+b, тогда и только тогда, когда существуют конечные пределы
Достаточные условия
![]() и
и
![]()
(или соответственно при x-)
Вертикальные
асимптоты
- асимптоты, параллельные оси ординат.
Если функция f(x) в точке x0
имеет бесконечный разрыв, то уравнение
x=x0
есть уравнение вертикальной асимптоты
графика этой функции. Для отыскания
вертикальных
асимптот
нужно найти такие значения х = а, при
приближении к которым функция y = f(x)
стремится к бесконечности. Тогда прямая
х = а будут вертикальной асимптотой.
Условие:
![]()
