МАТАН / Formulas (lim)

1. Определение предела функции в точке.

Теорема о пределе суммы двух функций.

Пределом ф-ции y=f(x) в точке x₀ называется такое число A, что для любого положительного e найдется такое положительное число d, что для всех значений x из d окрестности точки x₀ выполняется неравенство ½f(x)-A½<e

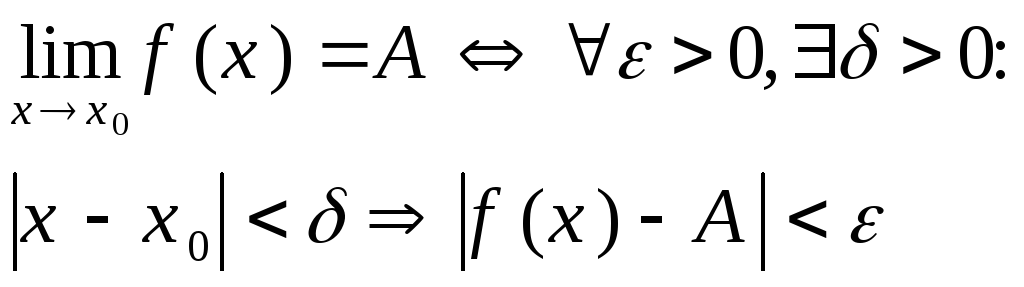
Если существует предел каждого из слагаемых, то существует и предел их суммы, равный сумме пределов слагаемых.

Дано:

Док-ть: Док-во:

Обозначим

Тогда найдутся такие бесконечно малые a(x) и b(x), для которых:

f(x)=A+a(x), g(x)=B+b(x).

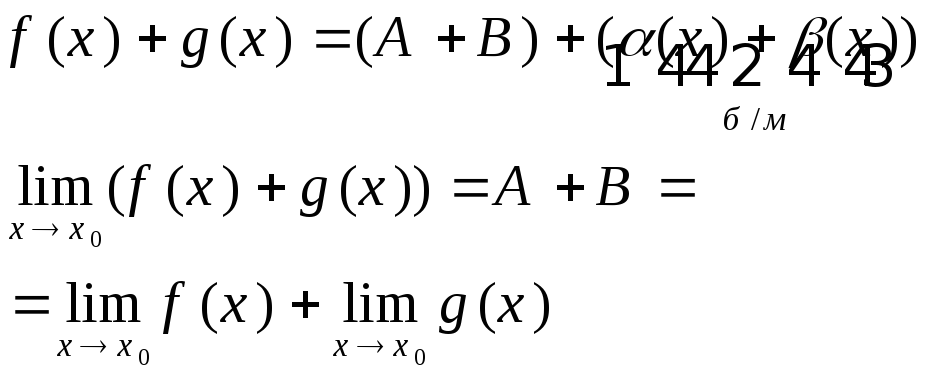
2. Определение предела ф-ции в точке.

Теорема о пределе произведения 2 функций.

Пределом ф-ции y=f(x) в точке x₀ называется такое число A, что для любого положительного e найдется такое положительное число d, что для всех значений x из d окрестности точки x₀ выполняется неравенство ½f(x)-A½<e

Если существует предел каждого сомножителя, то существует предел произведения, который равен произведению пределов сомножителей.

Дано:

Док-ть:

Док-во:

Обозначим

Тогда найдутся такие бесконечно малые a(x) и b(x), что:

f(x)=A+a(x), g(x)=B+b(x).

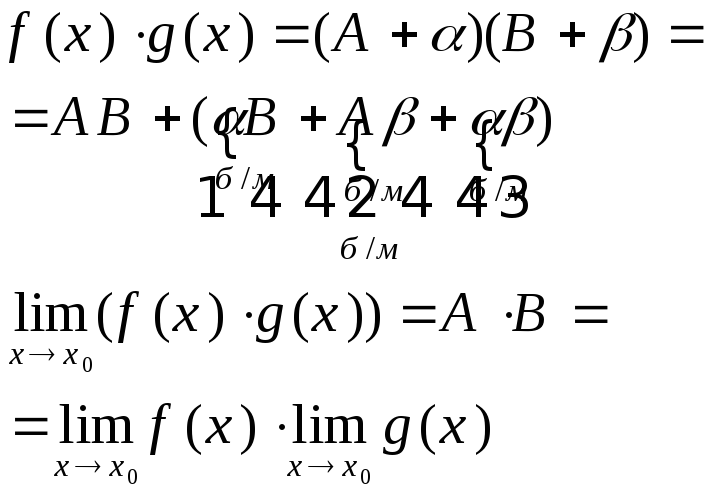
3. Определение касательной и нормали к плоской кривой. Вывод их уравнений.

Касательной к данной кривой в данной на ней точке M₀ называется предельное положение секущей при условии, что точка M₁, перемещаясь по этой кривой, неограниченно приближается к точке M₀.

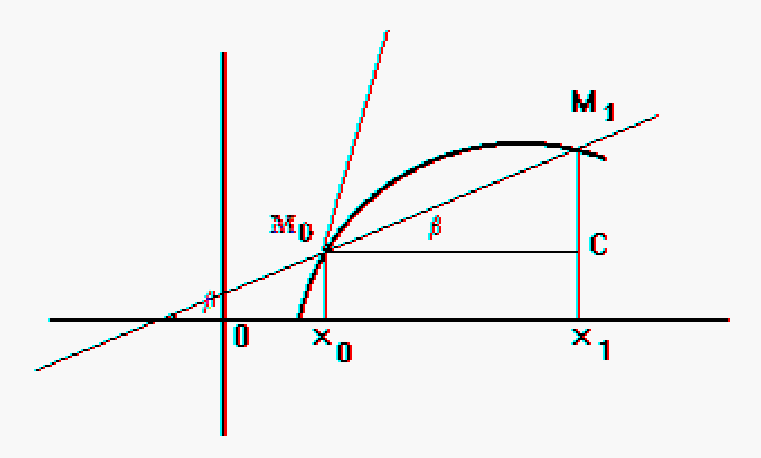Рассм. M₀CM₁: M₀(x₀;y₀) M₁(x₁,y₁)

tgb=M₁C/M₀C M₀C=x₁-x₀=Dx M₁C=y₁-y₀=Dy

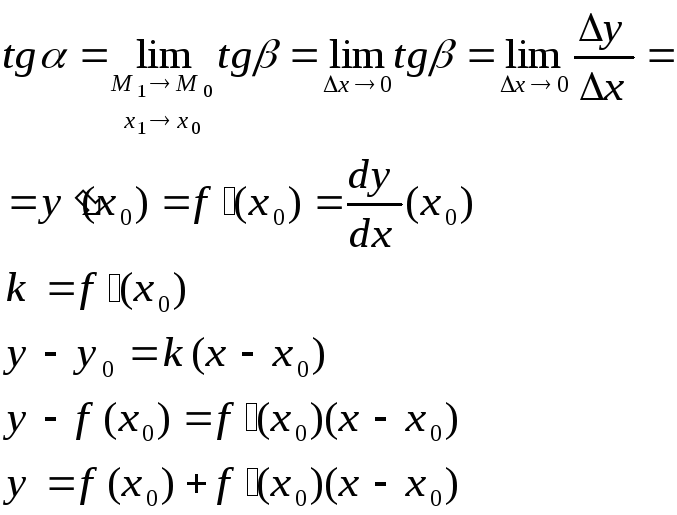
Нормалью данной кривой в данной на ней точке называется прямая, проходящая через эту точку перпендикулярно касательной в этой точке.

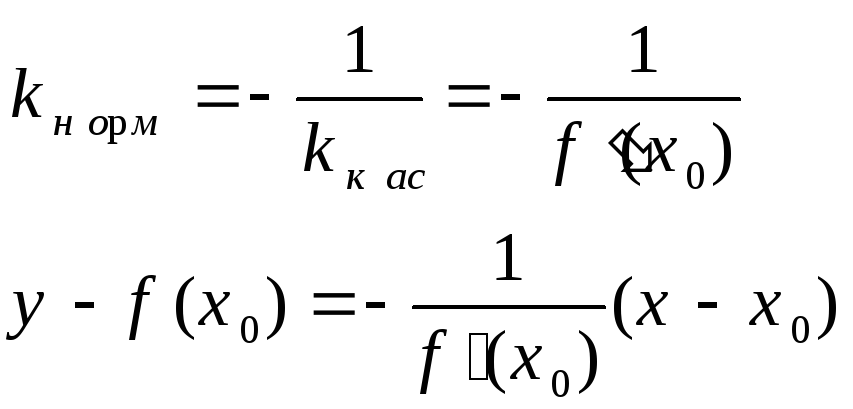
4. Определение непрерывности и дифференцируемости функций. Теорема о связи непрерывности и дифференцируемости.

Функция y=f(x) называется непрерывной в точке x=x₀, если она определена в некоторой окрестности точки x₀ (очевидно, и в самой точке x₀)и еслиили,что то же самое

Функция y=f(x) называется дифференцируемой в точке x=x₀, если ее приращение в этой точке может быть представлено в виде Dy=ADx+a(Dx)Dx, где A=const,

Если функция y=f(x) дифференцируема в точке x=x₀, то она непрерывна в этой точке.

Дано: Dy=f ‘(x₀)Dx+a(Dx)Dx

Док-ть:

Док-во:

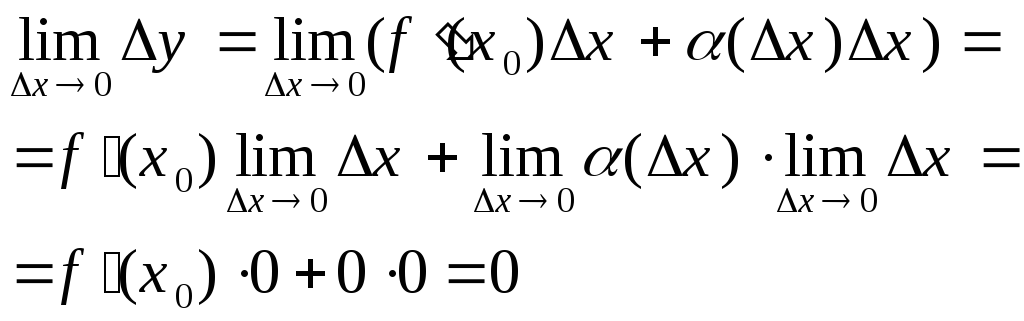
5. Определение производной. Теорема о производной суммы двух функций.

Производной от данной функции в данной точке называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к 0.

Производная суммы двух дифференцируемых функций равна сумме производных слагаемых.

y=u+v, u=u(x), v=v(x).

u и v диф. в т. x=x₀.

DxÞDu, DvÞDy

y+Dy=u+Du+v+Dv

Dy=u+Du+v+Dv-y= u+Du+v+Dv-u-v=Du+Dv

6. Определение производной. Теорема о производной произведения двух функций.

Производной от данной функции в данной точке называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к 0.

y=uv

Производная произведения двух дифференцируемых функций существует и вычисляется по формуле:

Док-во:

DxÞDu, DvÞDy

y+Dy=(u+Du)(v+Dv)=uv+Duv+uDv+DuDv

Dy= uv+Duv+uDv+DuDv-uv=Duv+uDv+DuDv

7. Вывод формул для производных sinx, cosx

y=sinx:

Dx; Dy=f(x₀+Dx)-f(x₀)

Dy=sin(x₀+Dx)-sinx₀=2sin(Dx/2)cos(x₀+Dx/2)

y=cosx:

Dx; Dy=f(x₀+Dx)-f(x₀)

Dy=cos(x₀+Dx)-cosx₀=-2sin(Dx/2)sin(x₀+Dx/2)

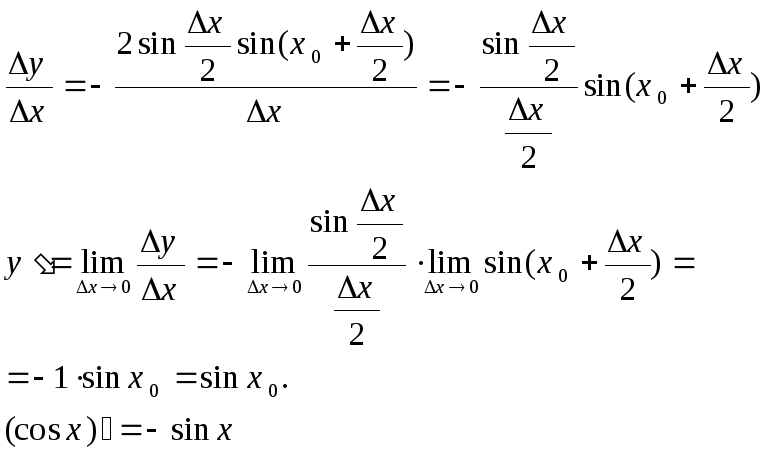
8. Вывод формулы производной сложной функции.

Если функция x=j(t) дифференцируема в точке t₀, а функция y=f(x) дифференцируема в точке x=x₀=j(t₀), то сложная функция y=f(j(t)) дифференцируема в точке t=t₀ и ее производная в этой точке находится по формуле

Док-во:

Т. к. функция y=f(x) дифференцируема в точке x=x₀, то Dy=f ‘(x₀)Dx+a(Dx)Dx.

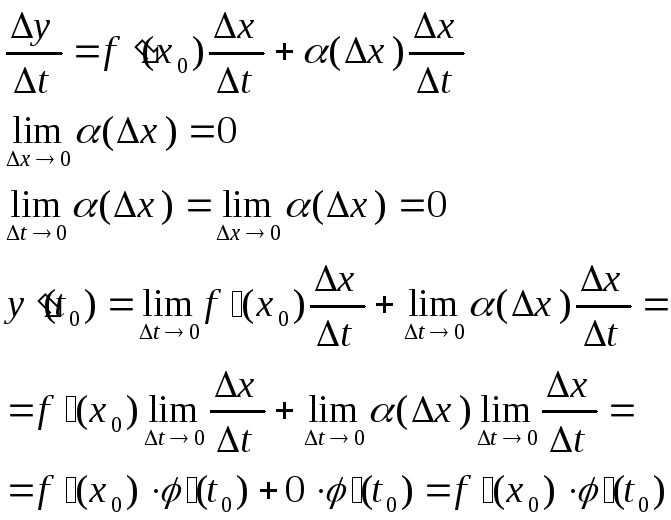
9. Вывод формулы для производной логарифмической функции.

10. y=arcsinx. Определение. Вывод производной.

arcsinx - угол, синус которого равен x.

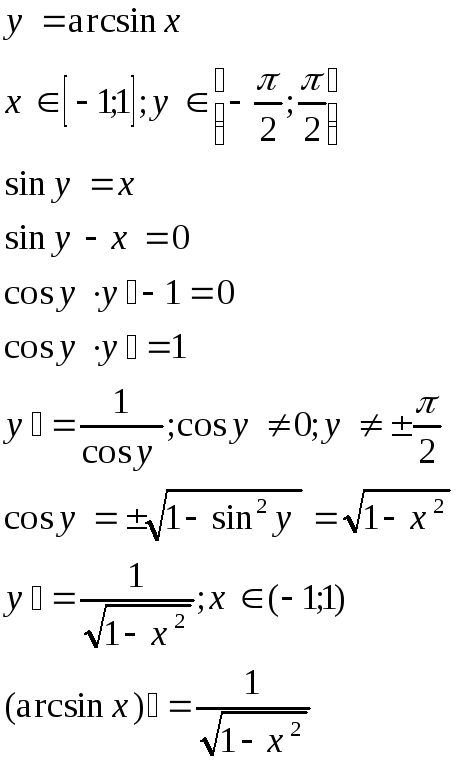
при x=±1 производной не существует

11. Вывод производных показательной и степенной функций.

Производная показательной функции:

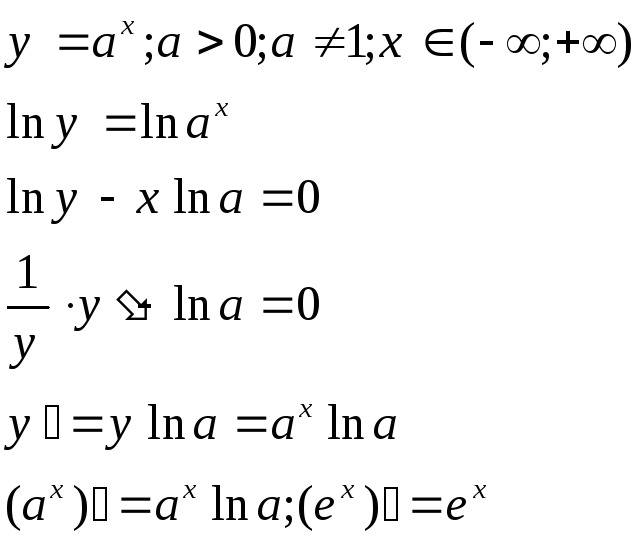
Производная степенной функции:

12. Дифференциал функции. Определение. Свойство инвариантности формы дифференциала.

Дифференциалом дифференцируемой функции называется главная, линейная относительно Dx, часть приращения функции.

Форма дифференциала функции f(x) не зависит от того, является ли x независимой переменной или функцией другого независимого переменного.

Док-во:

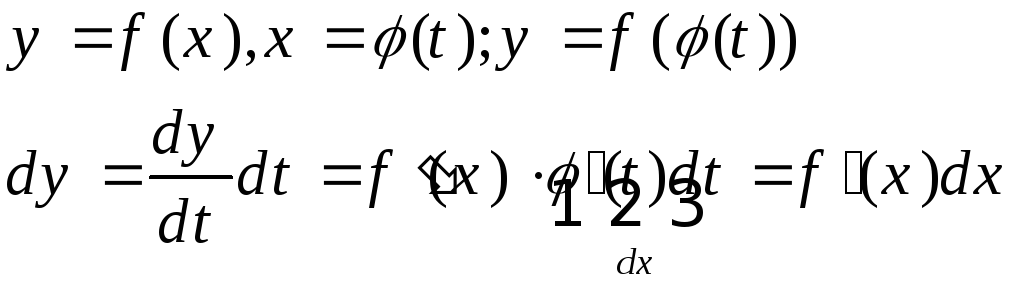
13. Определение максимума и минимума. Док-во необходимого условия экстремума.

Функция y=f(x) имеет максимум [минимум] в точке x=x₀, если найдется такая окрестность этой точки, что для всех x из этой окрестности выполняется неравенство f(x₀)>f(x) [f(x₀)<f(x)].

Если функция y=f(x) имеет в точке x=x₀ экстремум, то ее производная в этой точке равна 0 или не существует(???).

Дано: x=x₀ -точка максимума.

Док-ть: f ‘(x₀)=0.

Док-во:

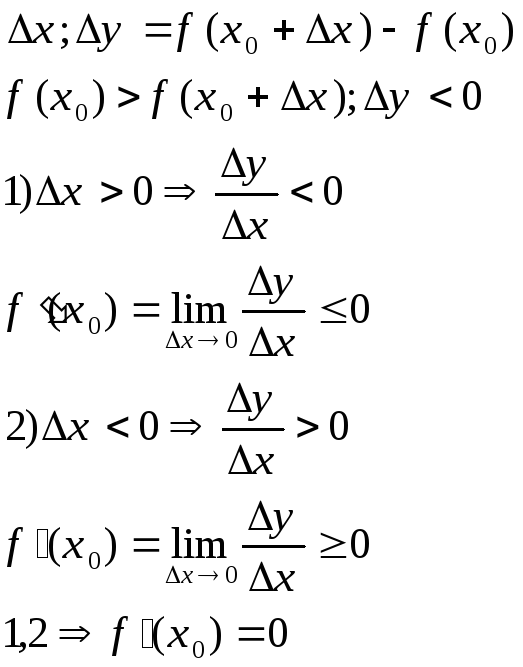
(для минимума - по аналог. док-ву)

14. Определение максимума и минимума. Доказательство достаточных условий экстремума.

Функция y=f(x) имеет максимум [минимум] в точке x=x₀, если найдется такая окрестность этой точки, что для всех x из этой окрестности выполняется неравенство f(x₀)>f(x) [f(x₀)<f(x)].

Если функция y=f(x) непрерывна в точке x=x₀ и дифференцируема в некоторой окрестности этой точки, и если при переходе через эту точку производная меняет знак, то в этой точке функция имеет экстремум: если знак f ‘(x) меняется с “+” на “-” - то функция имеет максимум в этой точке; если с “-” на “+” - то минимум.

Док-во:

Функция f(x) удовлетворяет всем условиям теоремы Лагранжа.

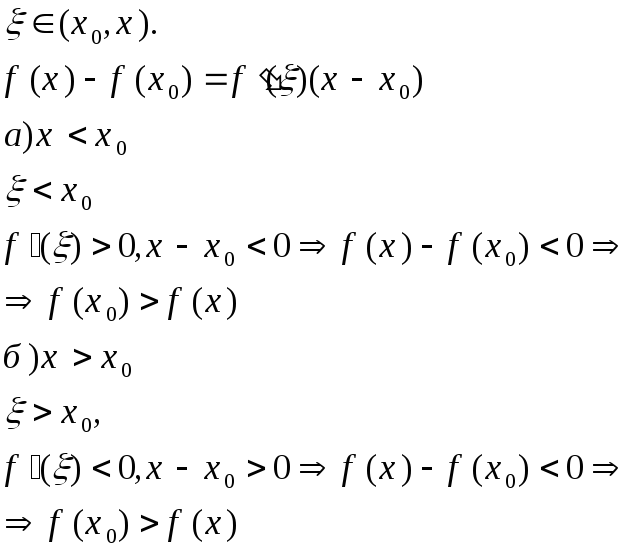
15. Возрастание, убывание функции. Теорема о достаточном условии монотонности функции.

Функция y=f(x) называется возрастающей [убывающей] на интервале (a;b), если из неравенства x₂>x₁ следует неравенство f(x₂)>f(x₁) [f(x₂)<f(x₁)] при условии, что (x₁;x₂)Ì(a;b).

Если функция y=f(x) дифференцируема на интервале (a;b) и f ‘(x)>0 [f ‘(x)<0] на этом интервале, то эта функция возрастает [убывает] на этом интервале.

Д-во:

Возьмем две произвольные точки: x₁,x₂Î(a;b);

x₀Î(a;b), x₂>x₁.

Рассм. отрезок [x₁,x₂]. На нем функция y=f(x) удовлетворяет всем условиям теоремы Лагранжа.

По теореме Лагранжа найдется xÎ(x₁;x₂), что выполняется равенство f(x₂)-f(x₁)=f ‘(x)(x₂-x₁).

1) f ‘(x)>0 Þ x₂-x₁>0 ; f ‘(x)>0 Þf(x₂)-f(x₁)>0

f(x₂)>f(x₁).

2) f ‘(x)<0

f ‘(x)<0

x₂-x₁>0Þf(x₂)-f(x₁)<0

f(x₂)<f(x₁)

1. Определение первообразной, неопределенного интеграла. Теорема об общем виде первообразной.

Функция F(x) называется первообразной от функции f(x) на данном промежутке, если для всех x из этого промежутка выполняется равенство F ‘(x)=f(x)

Неопределенным интегралом от функции f(x) на данном промежутке называется множество всех первообразных для функции f(x) на этом промежутке.

Если F₁(x) и F₂(x) - две первообразные от функции f(x) на одном и том же промежутке, то найдется такое C₁, что будет выполняться равенство F₂(x)=F₁(x)+C₁

Док-во:

Составим функцию j(x)=F₂(x)-F₁(x)

j‘(x)=F₂’(x)-F₁’(x)=f(x)-f(x)=0

Рассм. отр [x₁,x₂] Î(a,b)

j(x₁)=C₁ j(x₂)=C₁ (надо док-ть)

j(x) на [x₁,x₂] удовлетворяет всем условиям теоремы Лагранжа:

1) непрерывна на [x₁,x₂]

2) дифференцируема на (x₁,x₂)

xÎ(x₁,x₂), j(x₂)- j(x₁)= j‘(x)(x₂-x₁)=0

j(x₂)= j(x₁)=C₁

j(x)=C₁

F₂(x)-F₁(x)=C₁

F₂(x)=F₁(x)+C₁

2. Теорема об интеграле с постоянным нижним и переменным верхним пределом.

Производная от интеграла с постоянным нижним и переменным верхним пределом по верхнему пределу равна подынтегральной функции при верхнем пределе.

Д-во:

Пусть ф-ция f(t), непрерывна на [a;b]

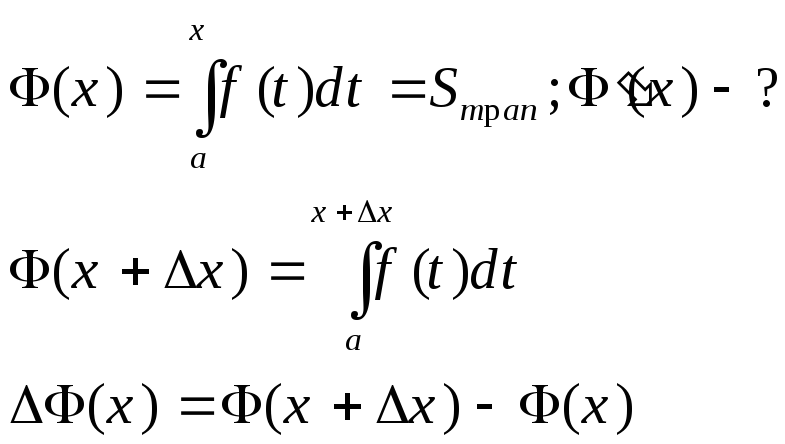
Пусть на отрезке [x; x+Dx] ф-ция f(t) принимает наименьшее значение m в точке h, наибольшее - М в точке x (m=f(h), M=f(x) ).

Тогда на этом отрезке

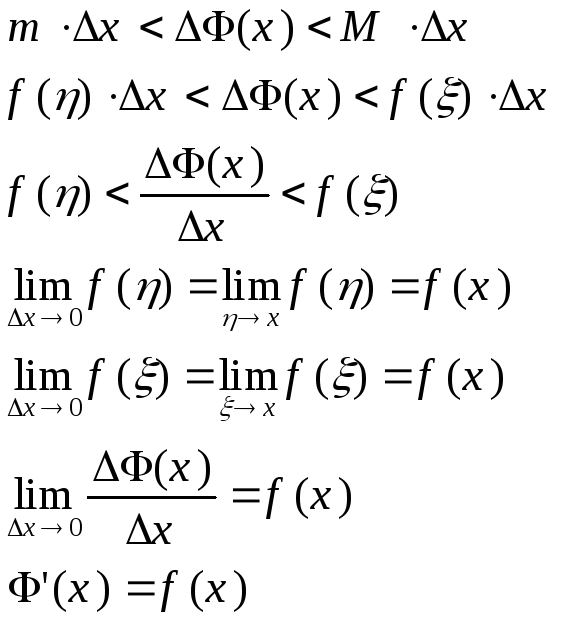
3. Вычисление определенного интеграла. Док-во формулы Ньютона-Лейбница.

Пусть F(x) - первообразная для f(x) на [a;b], т.е. F’(x)=f(x). Тогда найдется такое C₁, что

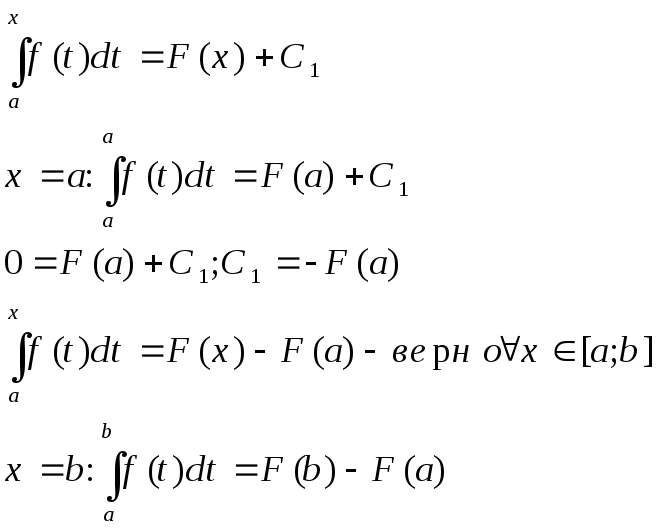
4. Теорема о замене переменной в определенном интеграле

Пусть x=j(t), tÎ[a;b], причем функция j(t) - возрастающая или убывающая на [a;b] - имеет на этом отрезке непрерывную производную j‘(t) и j(a)=a, j(b)=b.

Пусть F’(x)=f(x) на [a;b]

Рассм. F(j(t)) на [a;b]

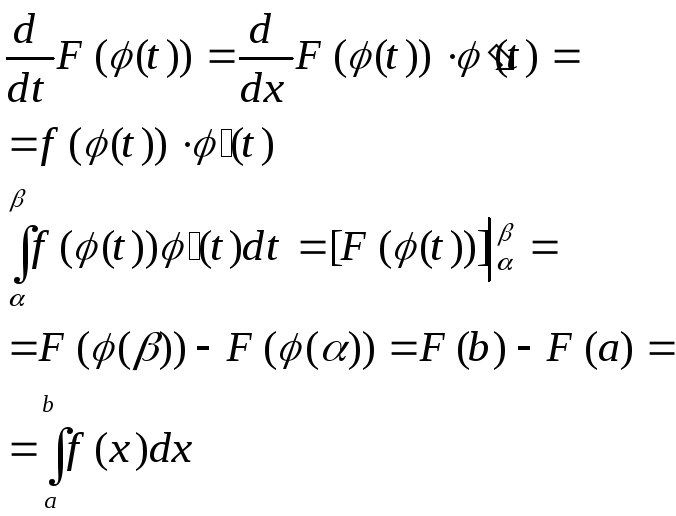
1. Определение предела функции в точке. Теорема о пределе дроби.

Пределом ф-ции y=f(x) в точке x₀ называется такое число A, что для любого положительного e найдется такое положительное число d, что для всех значений x из d окрестности точки x₀ выполняется неравенство ½f(x)-A½<e

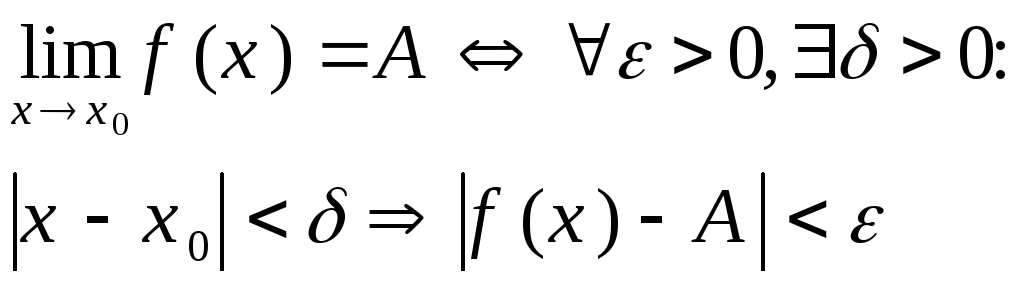
Если существуют предел числителя и предел знаменателя, причем предел знаменателя не равен 0, то существует предел дроби, равный пределу числителя, деленному на предел знаменателя.

2. Определение функции и ее области определения.

Если каждому значению x из некоторого числового множества E сопоставлено одно определенное значение переменной величины y, то говорят, что y является функцией независимой переменной x, а числовое множество E является областью определения данной функции.

3. Определение бесконечно малых и их свойства.

Функция a(x) называется бесконечно малой в точке x=x₀, если предел a(x) при x®x₀ равен 0.

Свойства:

1. Сумма бесконечно малых есть бесконечно малая.

2. Произведение бесконечно малых есть бесконечно малая.

3. Произведение бесконечно малой на ограниченную функцию есть бесконечно малая. (Функция f(x) называется ограниченной в точке x=x₀, если найдется такое число M и такая d-окрестность, что для всех x из d-окрестности выполняется неравенство ½f(x)½<M.)

4. Определение бесконечно большой. Ее связь с бесконечно малой.

Функция f(x) называется бесконечно большой в точке x=x₀, если для любого положительного M найдется такая d-окрестность этой точки, что для всех x из этой d-окрестности выполняется неравенство ½f(x)½>M.

Если f(x) - бесконечно большая в точке x=x₀, то функция a(x)=1/f(x) будет бесконечно малой в этой точке.

Если функция a(x) - бесконечно малая в точке x=x₀, то функция f(x)=1/a(x) будет бесконечно большой в этой точке.

5. Определение предела. Формулировка “теоремы о двух милиционерах”.

Пределом ф-ции y=f(x) в точке x₀ называется такое число A, что для любого положительного e найдется такое положительное число d, что для всех значений x из d окрестности точки x₀ выполняется неравенство ½f(x)-A½<e

Если в некоторой d - окрестности точки x₀ выполняется неравенство j(x)£f(x)£y(x) и

,то

6. Непрерывность функции.

Функция f(x) называется непрерывной в точке x=x₀, если ее предел в этой точке равен значению функции в этой точке.

Условия непрерывности:

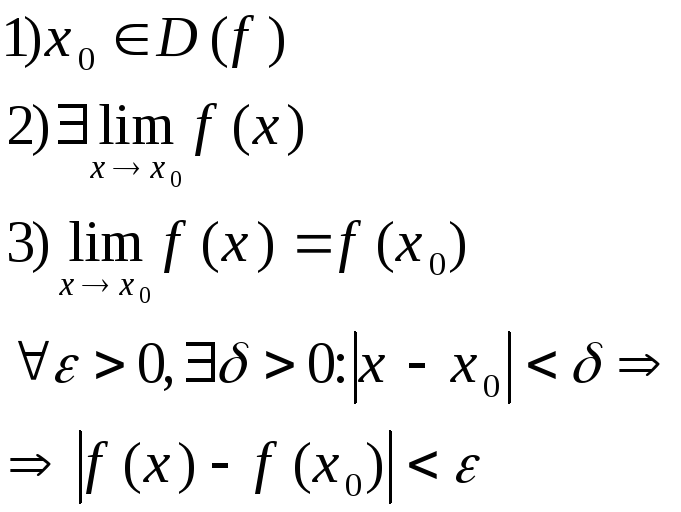
Функция y=f(x) называется непрерывной в точке x=x₀, если она определена в некоторой окрестности точки x₀ (очевидно, и в самой точке x₀)и еслиили,что то же самое

Функция y=f(x) называется непрерывной на данном промежутке, если она непрерывна в каждой точке этого промежутка.

7. Точки разрыва и их классификация.

Точка x=x₀ называется точкой разрыва функции y=f(x), если эта функция не является непрерывной в этой точке.

Точка x=x₀ называется точкой разрыва первого рода, если в этой точке существует предел слева и справа от этой функции.

Точка x=x₀ называется точкой разрыва второго рода, если хотя бы один из пределов слева и справа не существует.

8. Геометрический смысл дифференциала.

Дифференциалом дифференцируемой функции называется главная, линейная относительно Dx, часть приращения функции.

Дифференциал функции в данной точке равен приращению ординаты касательной.

9. Теорема Ролля.

Если функция y=f(x) непрерывна на отрезке [a;b], дифференцируема в каждой внутренней точке этого отрезка и на его концах обращается в нуль, то внутри отрезка [a;b] найдется такая точка x, что f ‘(x)=0.

10. Геометрический смысл теоремы Ролля.

Если функция y=f(x) удовлетворяет на отрезке [a;b] всем условиям теоремы Ролля, то на графике функции найдется такая точка, касательная в которой параллельна оси абсцисс.

11. Теорема Лагранжа.

Если функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема в каждой внутренней его точке, то внутри отрезка [a;b] найдется такая точка x, что выполняется равенство

f(b)-f(a)=f ‘(x)(b-a).

12. Геометрический смысл теоремы Лагранжа.

Если функция y=f(x) на отрезке [a;b] удовлетворяет всем условиям теоремы Лагранжа, то на дуге, являющейся графиком этой функции, найдется такая точка, касательная в которой будет параллельна хорде, стягивающей эту дугу.

13. Определение выпуклости и вогнутости графика функции. Достаточные условия.

График функции y=f(x) называется выпуклым [вогнутым] в точке (x₀;f(x₀)), если в этой точке существует касательная к этому графику, которая в некоторой окрестности этой точки расположена выше [ниже] этой кривой.

График функции y=f(x) называется выпуклым [вогнутым] на интервале (a;b), если он выпуклый [вогнутый] в каждой точке этого интервала.

Если функция y=f(x) дважды дифференцируема на интервале (a;b) и ее вторая производная отрицательна [положительна] во всех точках этого интервала, то график функции y=f(x) является выпуклым [вогнутым] на этом интервале.

14. Определение точки перегиба. Достаточные условия.

Точка (x₀;f(x₀)) называется точкой перегиба графика функции y=f(x), если в этой точке существует касательная и если она отделяет интервал выпуклости от интервала вогнутости.

Пусть функция y=f(x) дважды дифференцируема в некоторой окрестности точки x=x₀, и в точке (x₀;f(x₀)) существует касательная к графику этой функции. Если при переходе через точку x=x₀ вторая производная меняет знак, то точка (x₀;f(x₀)) является точкой перегиба графика функции.

15. Определение асимптоты к графику функции и нахождение невертикальной асимптоты.

Асимптотой данной кривой называется такая прямая, что расстояние от точки на кривой до этой прямой стремится к нулю при неограниченном удалении этой точки от начала координат.

Наклонные (невертикальные) асимптоты - асимптоты, не параллельные оси oy. Кривая, заданная уравнением y=f(x) имеет невертикальную асимптоту, определяемую уравненем y=kx+b, тогда и только тогда, когда существуют конечные пределы

и

(или соответственно при x®-¥)

16. Теорема о среднем для определенного интеграла.

Если функция f(x) непрерывна на отрезке [a;b], то внутри этого отрезка найдется такая точка x, что выполняется равенство:

Кривые второго порядка.

Общий вид уравнения:

Ax²+By²+Cx+Dy=F, причем A и B одновременно не равны нулю.

Каноническое уравнение:

I. A,B ¹0

1) A×B>0

a) a=b Þ (x-x₀)²+(y-y₀)²=a²

окружность с центром O(x₀;y₀) R=a

б) a¹b

Каноническое уравнение:

- эллипс

ox,oy - оси симметрии; O(0;0) - центр

A₁(-a;0),A₂(a;0),B₁(0;b),B₂(0;-b) - вершины

A₁A₂, B₁B₂ - оси; F₁,F₂ - фокусы

F₁(c;0), F₂(-c;0)

В общем случае центр - (x₀,y₀).

Эллипс - геометрическое место точек,

расстояние до которых от двух данных

точек, называемых фокусами, постоянно

(и равно большой оси эллипса).

2) AB<0

Каноническое уравнение:

- гипербола

O(0;0) - центр; (-a;0),(a;0) - действительные

вершины; (0;b), (0;-b) - мнимые вершины;

A₁A₂-действительная ось; B₁B₂-мнимая ось;

F1(c;0), F2(-c;0) - фокусы;

Прямые и - асимптоты.

В общем случае центр - (x₀,y₀).

Гипербола - геометрическое место точек,

разность расстояний от которых до двух

фиксированных точек, называемых

фокусами, - величина постоянная.

Если a=b, то гипербола называется

равнобочной.

II. A=0, B¹0 Þ

A¹0, B=0 Þ

Каноническое уравнение: y²=2px

ox - ось симметрии; O(0;0) - вершина;

F(p/4;0) - фокус; x=-p/4 -директриса.

В общем случае вершина - (x₀,y₀).

Парабола - геометрическое место точек,

равноудаленных от данной точки, называемой