ВычМат_Лекции_2013_1 / Лекции Матлаб, программы и задачи к ним / 7 лекция Матлаб (Решение уравнений в частных производных) / 7 лекция Матлаб (Решение уравнений в частных производных)

МАТЛАБ. РЕШЕНИЕ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ.

Общие сведения о дифференциальных уравнениях в частных производных.

Модели различных процессов описываются с их помощью. Аргументами функций этих уравнений являются пространственные координаты х, y z и время t.

Линейным УрЧП 2 порядка называется для функции u(x,y) F(x,y) =

A(x,y)∂²u/∂x² + 2B(x,y)∂²u/∂x∂y + C(x,y)∂²u/∂y² + D(x,y)∂u/∂x + E(x,y)∂u/∂y + G(x,y)u

Линейным УрЧП 2 порядка называется для функции u(x,t) F(x,t) =

A(x,t)∂²u/∂x² + 2B(x,t)∂²u/∂x∂t + C(x,t)∂²u/∂t² + D(x,t)∂u/∂x + E(x,t)∂u/∂t + G(x,t)u

Если F=0 то уравнение называют однородным.

Если В²-АС<0 то эллиптическое уравнение.

Если В²-АС>0 то гиперболическое уравнение.

Если В²-АС=0 то параболическое уравнение.

Если В²-АС не имеет постоянного знака то уравнение смешанного типа. Можно преобразованием переменных привести уравнение к такому виду чтобы В=0. Тогда можно определить его тип (см. выше).

Использование метода сеток. Часто используют метод сеток (он же метод конечных разностей). Область поиска решения разбивается прямоугольной сеткой на клеточки. Точки (узлы сетки) на границе области поиска называются внешними, остальные внутренними. Рассматривая значения в узлах сетки, получаем (в зависимости от их количества) более или менее сложную для решения систему линейных алгебраических уравнений. Уменьшение числа узлов сетки снижает точность решения.

Можно выделить следующие этапы решения уравнений в частных производных:

• Конструирование (построение) области, в которой решается уравнение.

• Ввод уравнения в частных производных.

• Определение начальных и граничных условий.

• Триангуляция области.

• Решение уравнения.

• Визуализация результата.

В окне Command Window введем команду pdetool и откроется окно PDE ToolBox. Оно содержит:

• Строку меню;

• Панель рисования области;

• Панель определения и решения задачи;

• Область ввода формулы для конструирования области решения;

• Место для определения геометрической области решения задачи.

Решение эллиптических уравнений. Рассмотрим для примера следующую задачу: пусть дана пластина (неважно из какого материала). В ней два круглых отверстия, дана температура на их краях (то есть на окружностях в виде с соответствующего направления). Границы пластины правая и левая теплоизолированы, верхняя и нижняя не изолированы и дана их температура. Дан коэффициент температуропроводности.

Y H=2м

1 м d=0,6м d=0,6 м

х₀=0,7м х_n=2,5 м L=3м X

Дифференциальное уравнение, описывающее распределение температуры, можно записать следующим образом: a²(∂²u/∂x²+∂²u/∂y²)=0. Граничные условия на правой и левой границах имеют вид: na²(∂u/∂n)=0; где n вектор нормали к границе. Таким образом, задача о распределении тепла в данной области (области G) полностью описываются уравнением и граничными условиями.

Сначала установим границы области. Пойдем в pdetoolbox в меню Options-Axes Limits и укажем границы по х и по у. Пусть х от -1 до 4 и у от -1 до 3.

Отобразим сетку на координатной плоскости, нажмем Options-Grid.

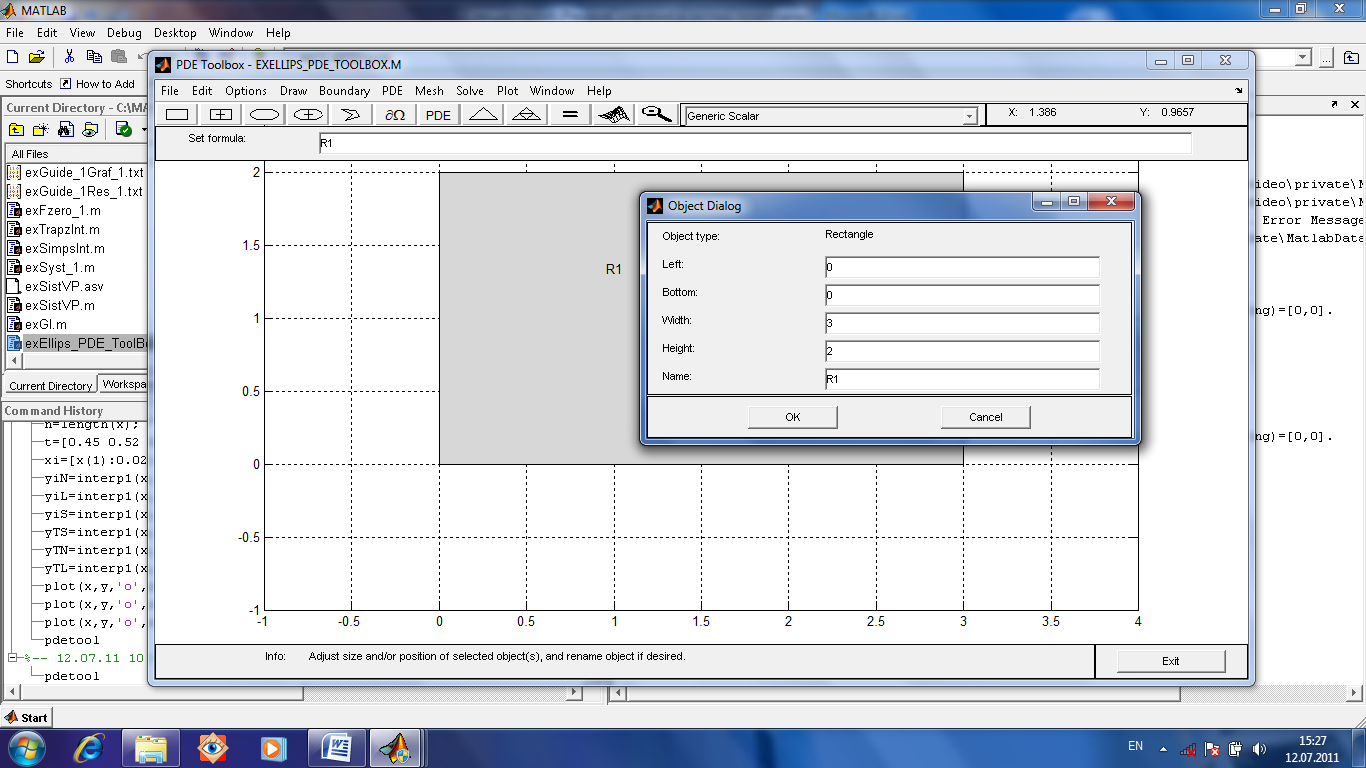
Теперь нарисуем прямоугольник размером 2 на 3. Для этого выберем его на панели рисования и расположим, ориентируясь по линиям сетки. Однако вручную не очень точно, поэтому дважды щелкнем прямоугольник и откроется Object Dialog, где можно более точно указать привязку (левый нижний угол) и размеры.

Затем нарисуем два круга (тем же образом), первый с центром в (1, 1) и радиусом 0.3, и второй с центром в (2.2, 1) и радиусом 0.3.

Есть операции вычитания объектов -, операция объединения объектов + и операция пересечения объектов *.

В области формулы введем R₁-C₁-C₂ , то есть из прямоугольника вычтем два круга.

Для ввода этого выражения (то есть чтобы вычитание произошло) нажмем PDE-PDE Mode и тогда на месте кругов будут дырки в прямоугольнике.

Зададим тип решаемой задачи в пункте меню Options-Applications-Heat Transfer.

Определим параметры уравнения в пункте меню PDE-PDE Specifications. Уравнение у нас a²(∂²u/∂x²+∂²u/∂y²)=0 с граничными условиями na²(∂u/∂n)=0. Оно эллиптическое (щелкнем переключатель Elliptic). Пусть коэффициент температуропроводности а²=225, на верхней и нижней границе области температура равна 580, на окружностях (краях отверстий) 450. Введем коэффициент температуропроводности в соответствующую строку, укажем также, что нет источников тепла, нет конвекции.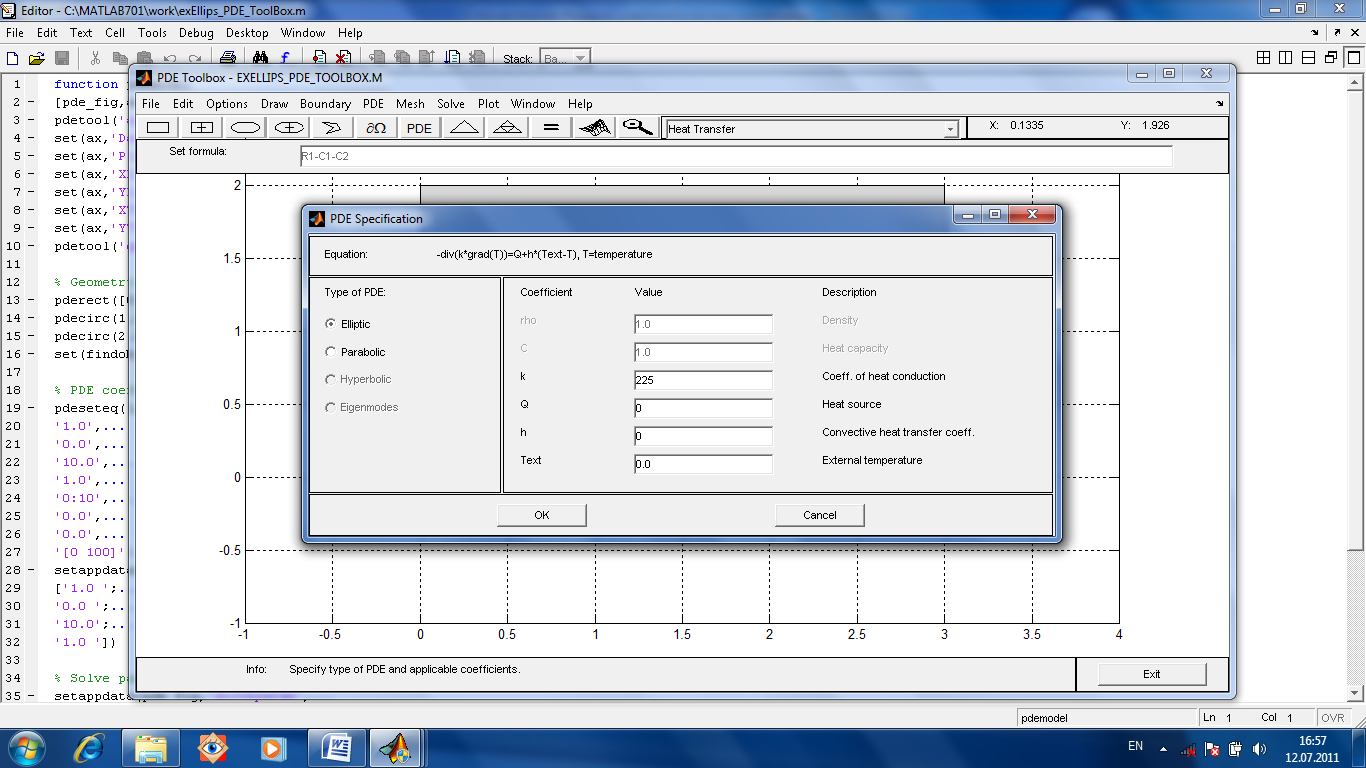

Определим граничные условия. Для этого щелкнем пункт меню Boundary-Boundary Mode. Появится возможность выделить участок границы. Если необходимо выделить несколько участков границы, то щелчок по каждому из них осуществляется при нажатой кнопке Shift. Выделим верхнюю и нижнюю границы области. Для определения условий идем в пункт меню Boundary-Specify Boundary Conditions. В окне Boundary Conditions выберем условия Дирихле. 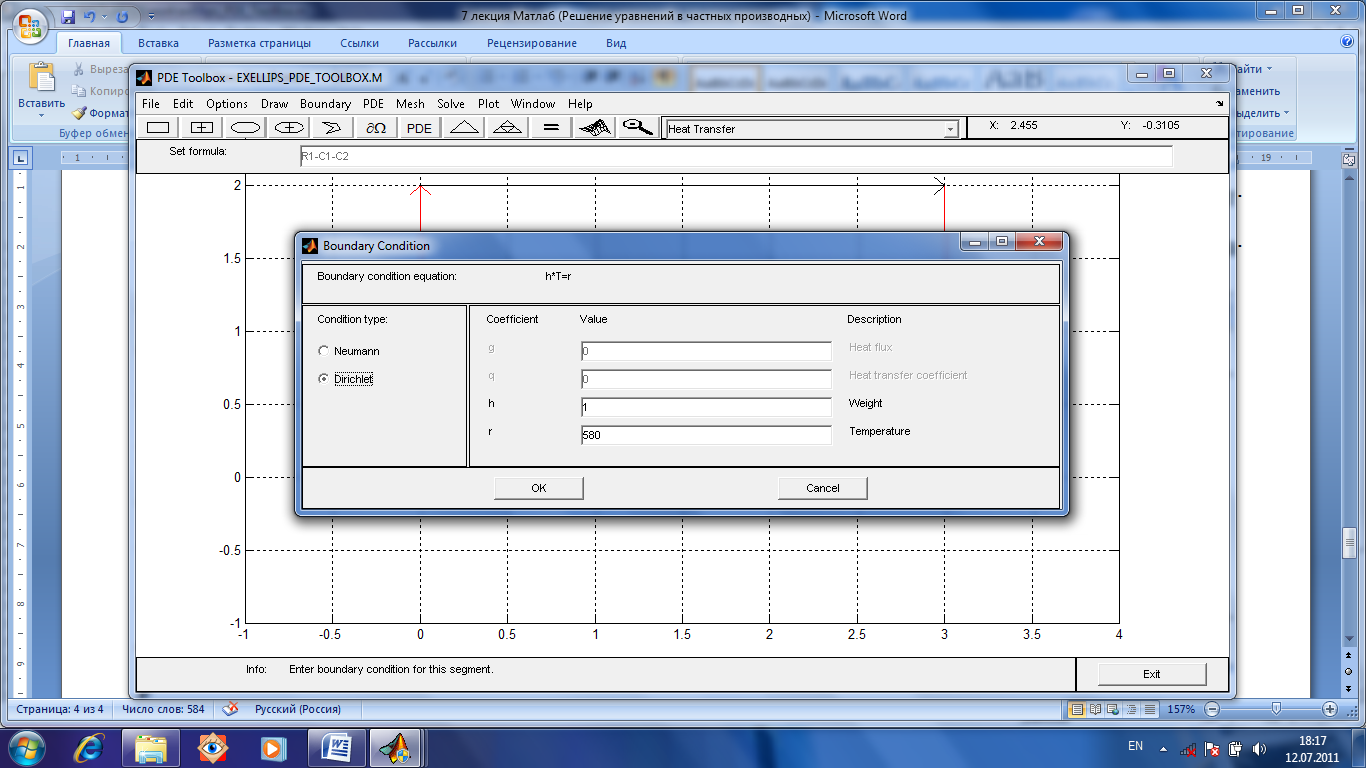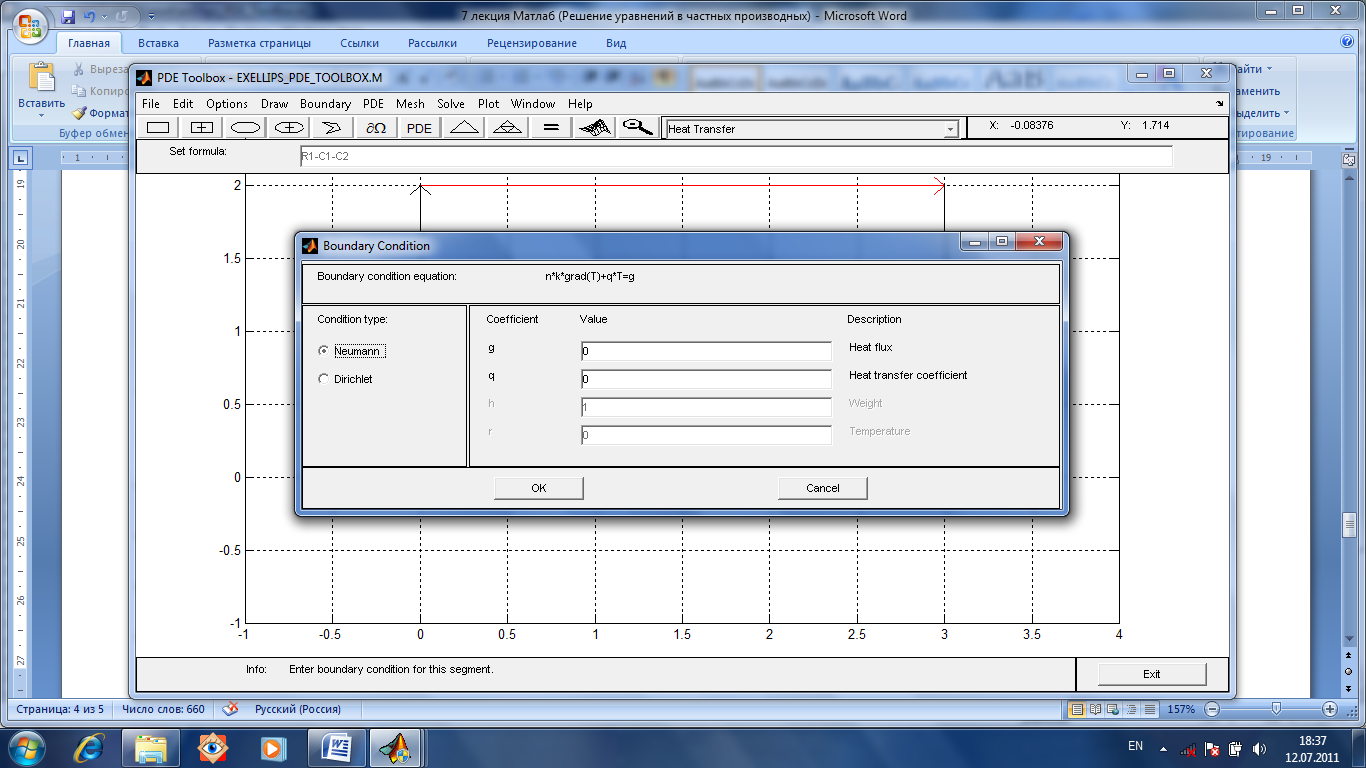Введем данные. Пусть температура равна 580. Затем выделим границы отверстий и установим для них температуру 450. После этого для левой и правой границ введем условия Неймана.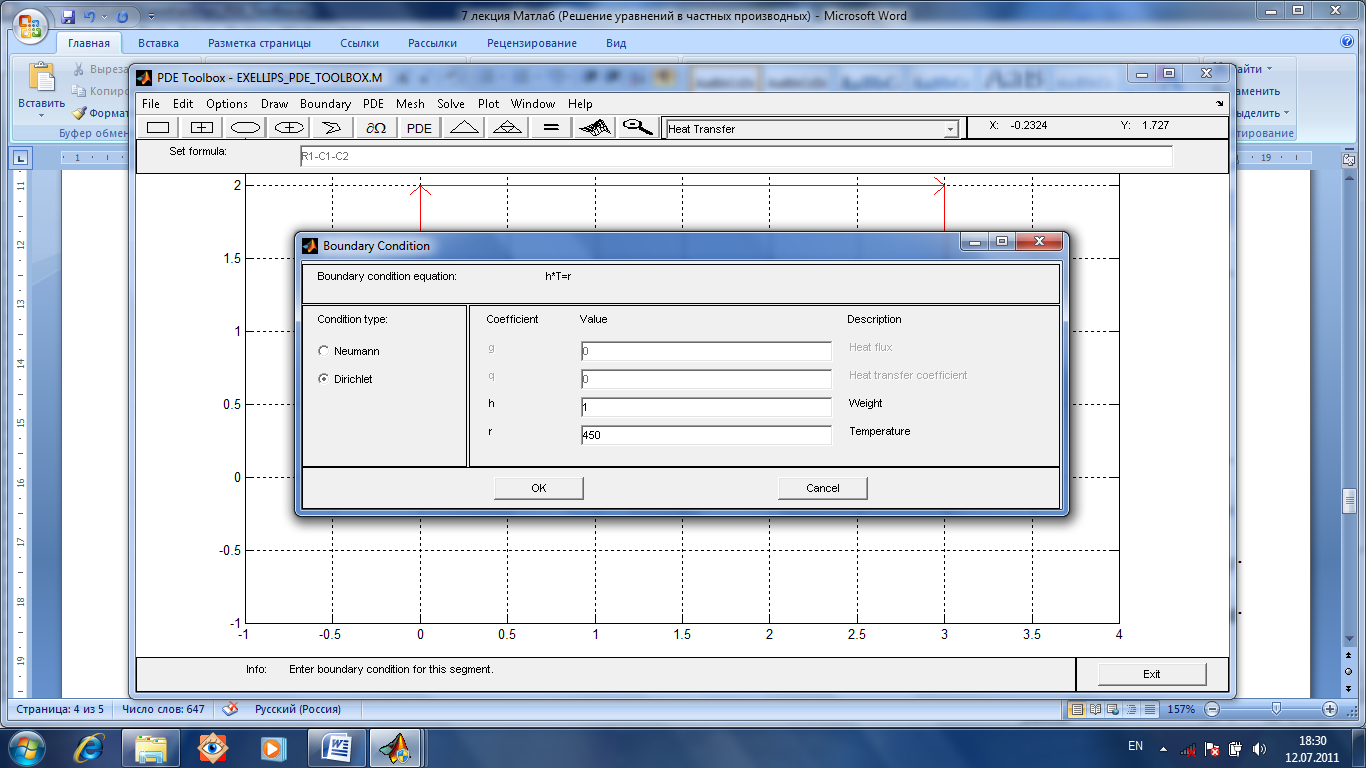

Теперь надо провести триангуляцию области (покрыть ее сеткой из треугольников).

Для этого нажмем пункт меню Mesh-Mesh Mode и получим крупные треугольники и деформированные отверстия. Для измельчения треугольников нажмем Mesh-Refine Mesh и так пару раз, пока края отверстий не станут круглыми. Чрезмерное измельчение сетки удлиняет время расчета.

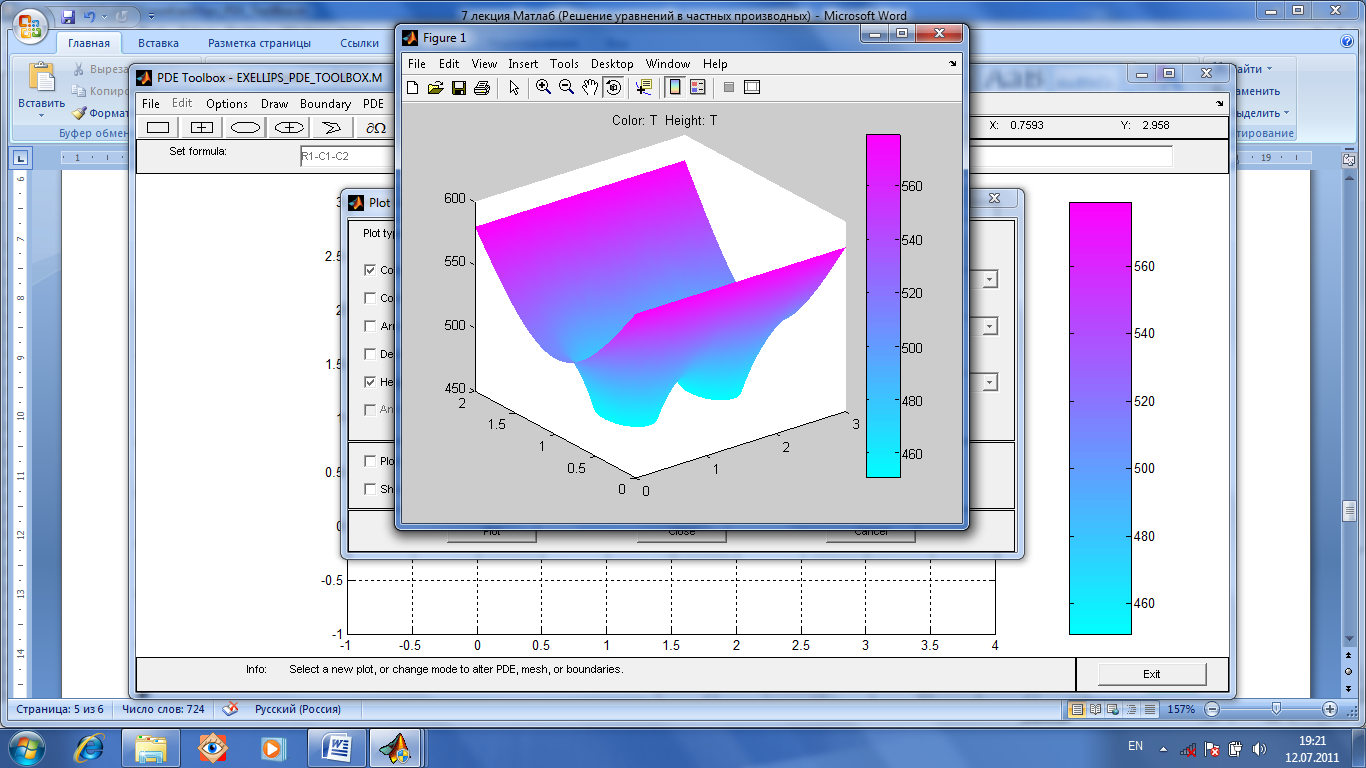
Для получения цветного графика надо нажать Solve-PDE Solve. Для получения трехмерного графика надо еще нажать Plot-Parameters и включить в открывшемся окне флажок Height (3-D Plot).

Для практики, решим уравнение ∂²u/∂x²+∂²u/∂y²=-x-y в области G(-1≤x≤1; -1≤y≤1) при u(x,y)=0 на границе области. Построим область, в которой будем искать решение. Затем, помня что канонический вид уравнения A(x,y)∂²u/∂x² + 2B(x,y)∂²u/∂x∂y + C(x,y)∂²u/∂y² + D(x,y)∂u/∂x + E(x,y)∂u/∂y + G(x,y)u = F(x,y), и посмотрев повнимательней на то уравнение, которое решаем, приходим к выводу, что коэффициенты A=1, B=0, C=1, D=0, E=0, G=0, F=x+y, а само уравнение эллиптическое, так как В²-АС<0. Вводим в окне PDE Specification значения коэффициентов.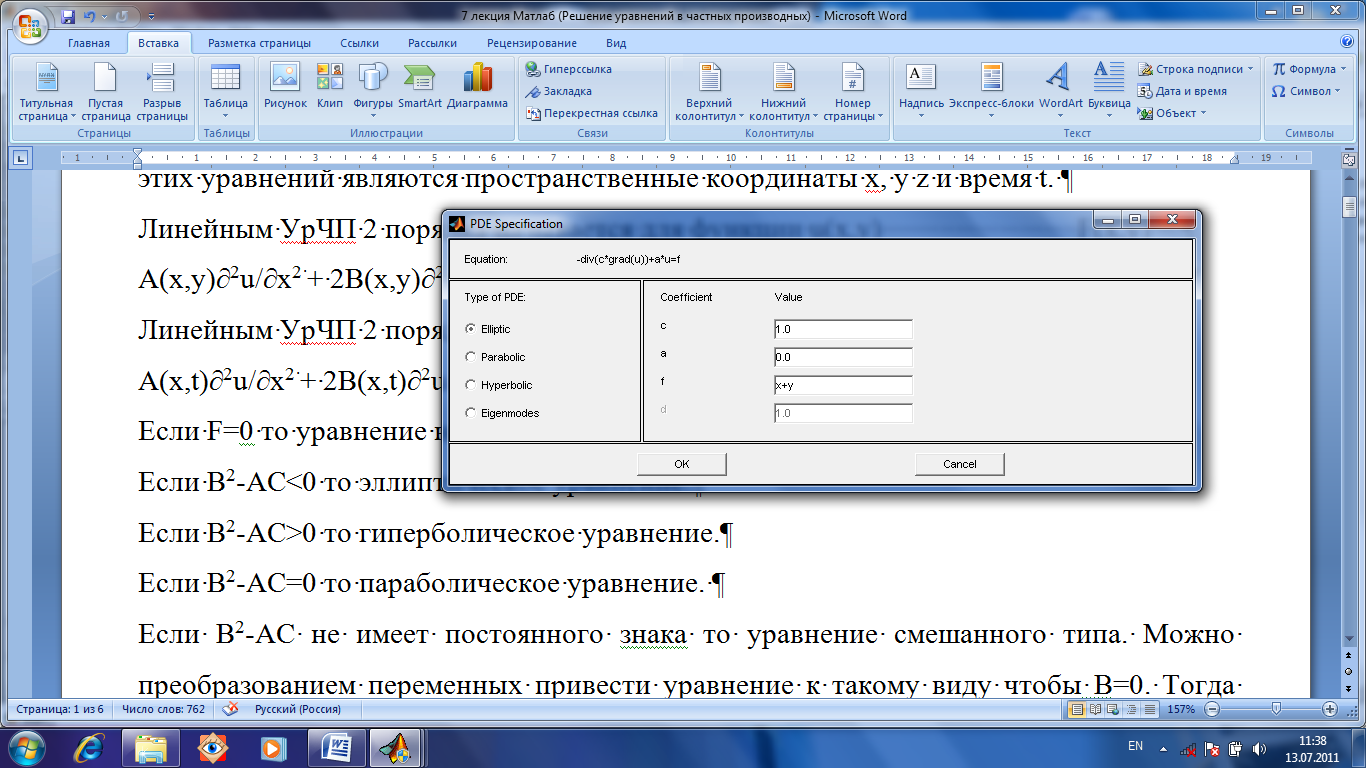

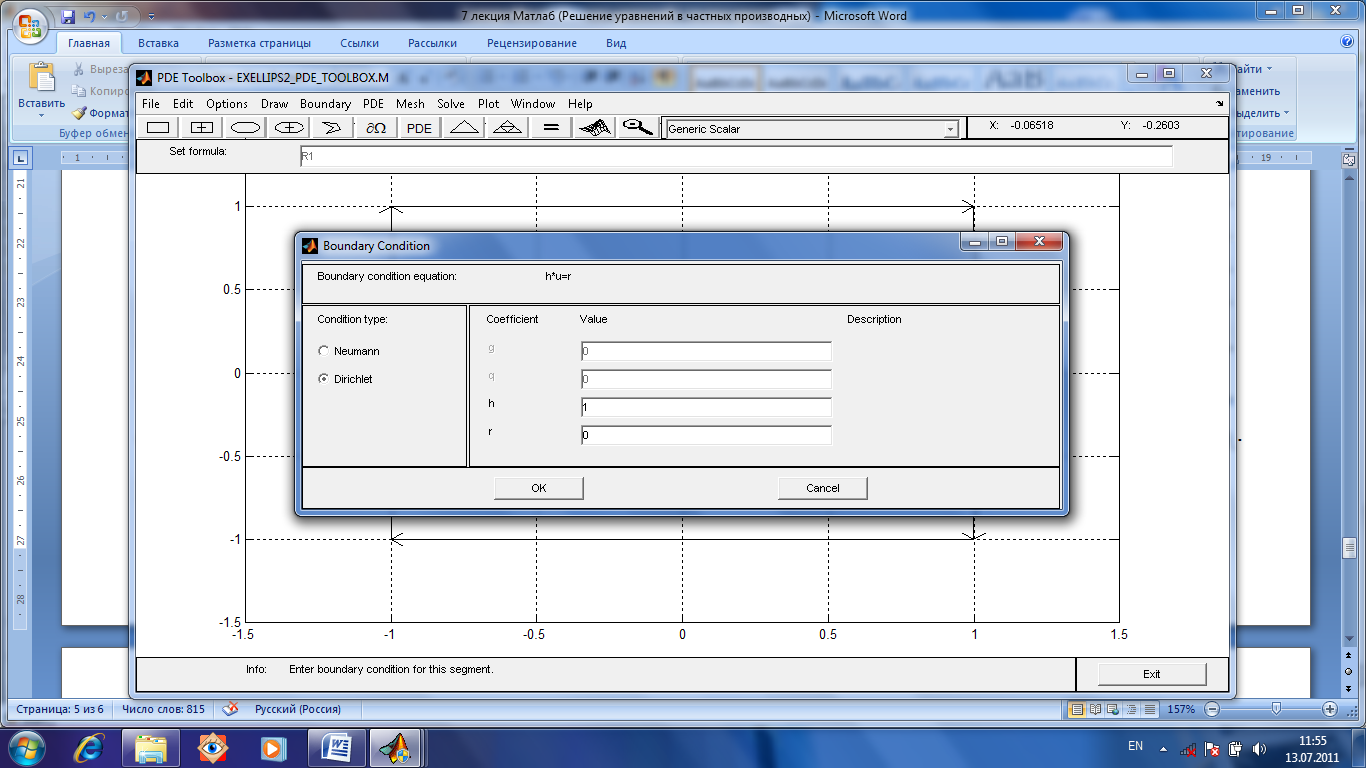
Затем выделить стороны (границы области) и определим на них граничные условия. Зная что u(x,y)=0 на границе области, введем соответствующие значения коэффициентов в окне Boundary Condition.

После этого произвести триангуляцию области.

Затем запустить расчеты и получить график решения.

Отредактировать его хорошенько, повернуть поудобнее, наложить сетку и так далее.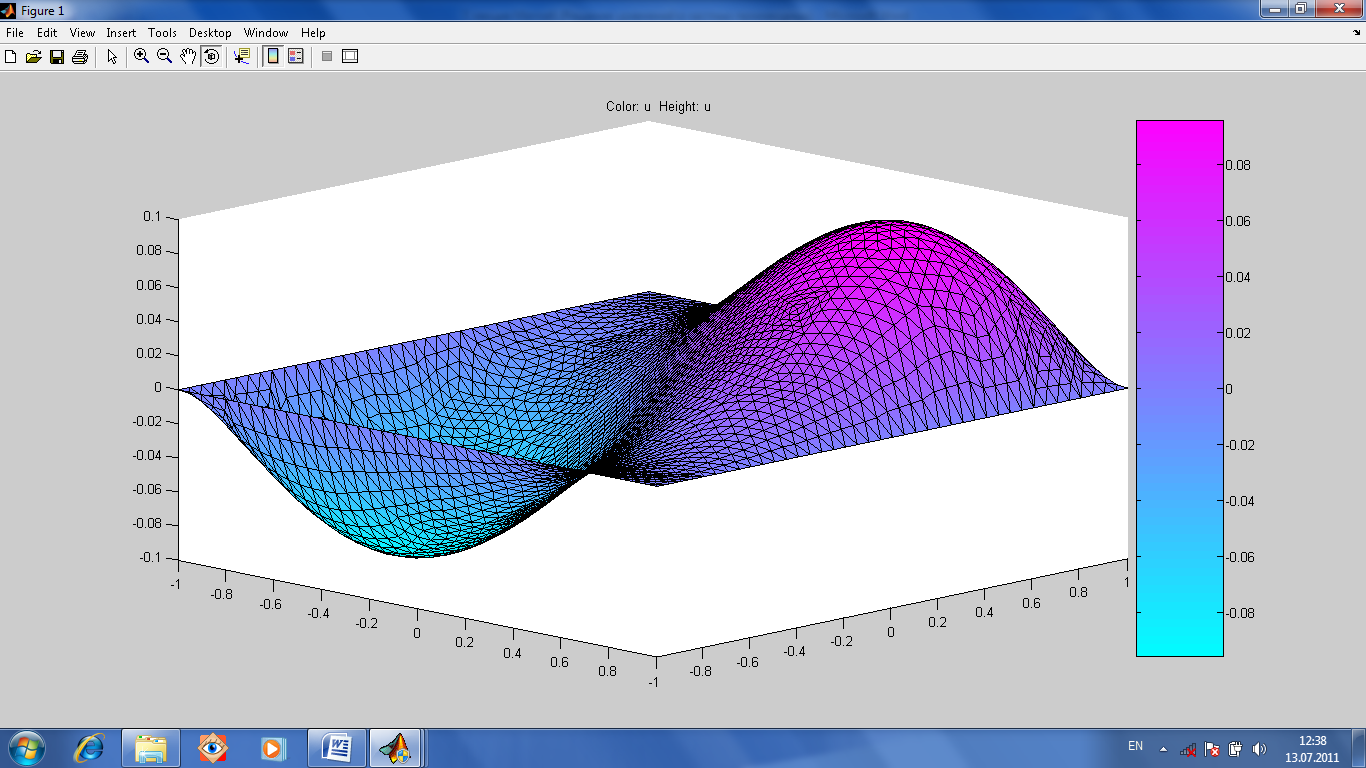

Решение нестационарных задач (гиперболических и параболических уравнений).

Рассмотрим задачу о колебаниях прямоугольной мембраны. Уравнение ее колебаний имеет вид ∂²u/∂t²=a²(∂²u/∂x²+∂²u/∂y²) при условиях u(0,y,t)=u(l₁,y,t)=u(x,0,t)=u(x,l₂,t)=0, а также при u(x,y,0)=Axy(l₁-x)(l₂-y), и при u_t(x,y,0)=0.

Пусть например l₁=2, l₂=3, A=1, a=2.

Зададим область решения по х(0, 2) и по у(0, 3). Затем определяем гиперболическое уравнение и его коэффициенты.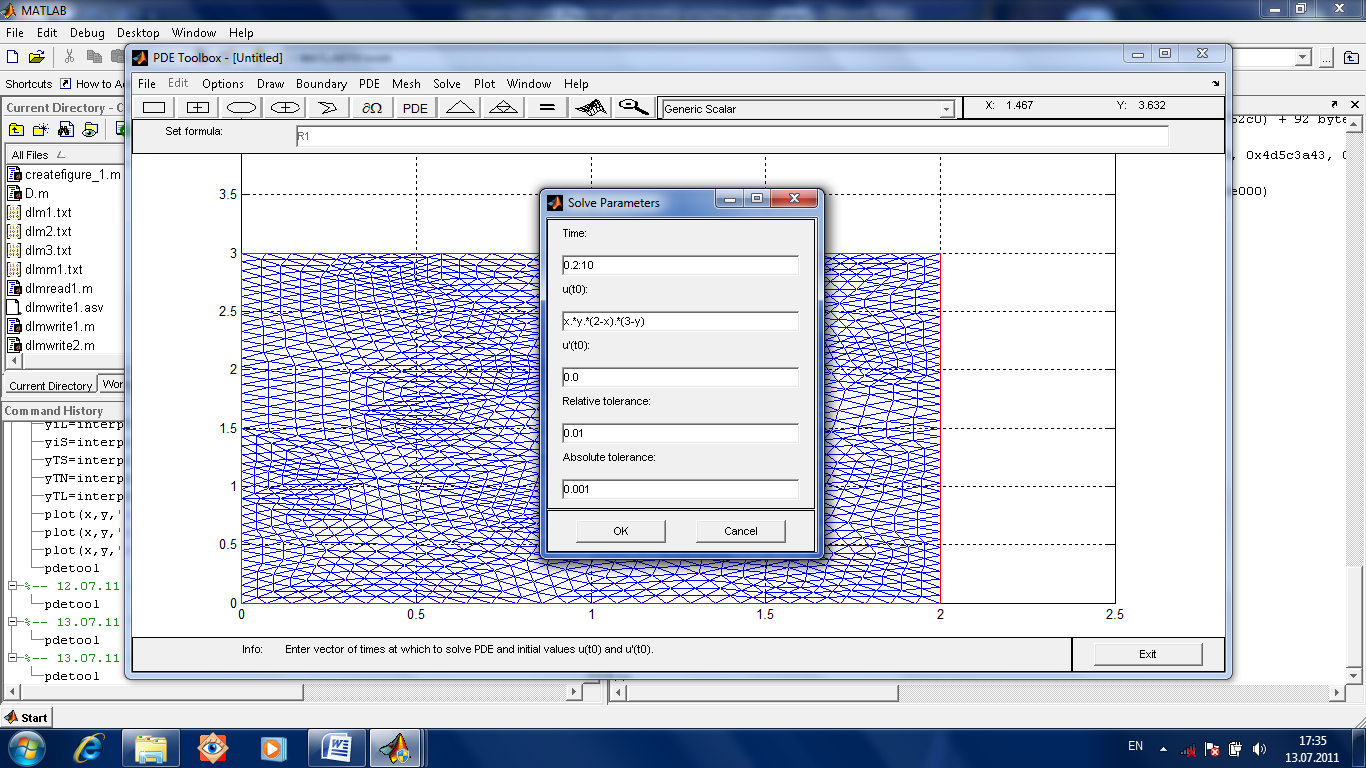

После этого определяем нулевые условия на границе.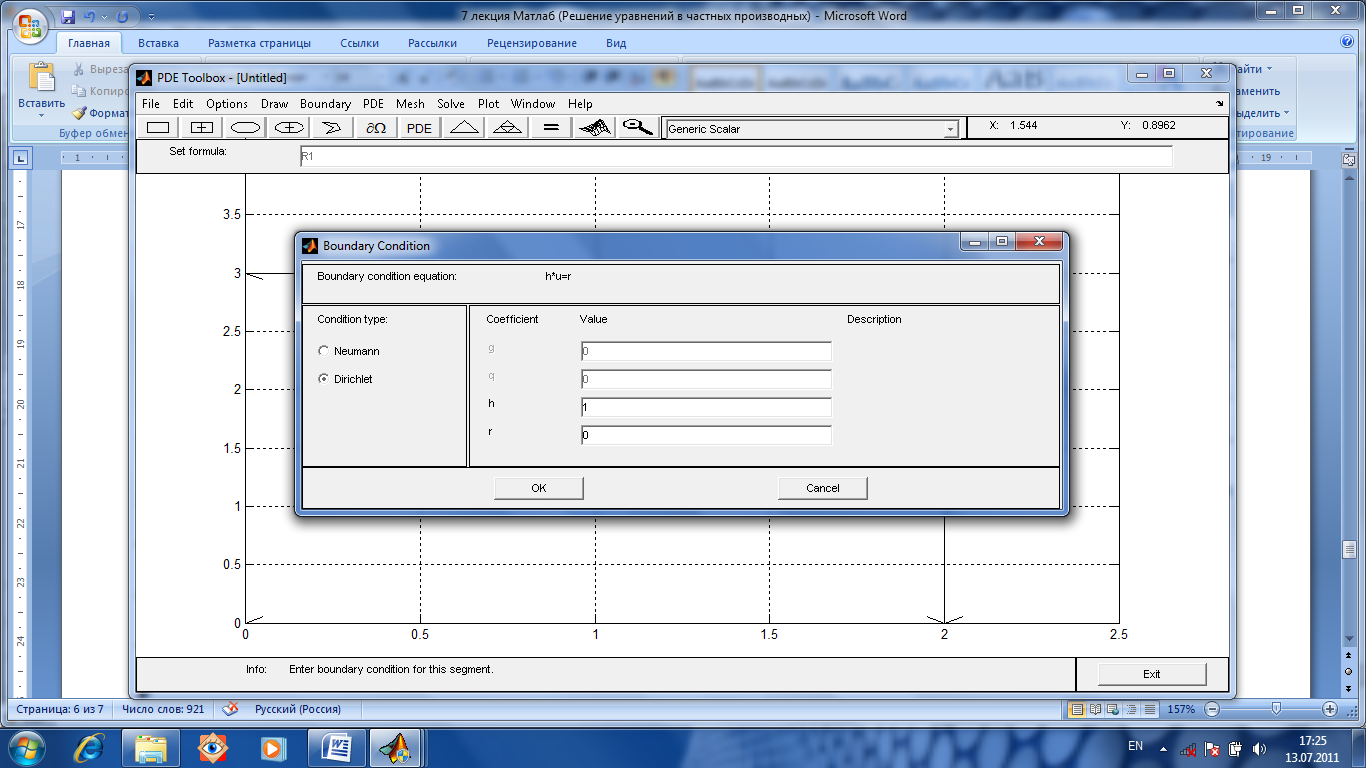

В отличие от рассмотренных ранее эллиптических уравнений, необходимо определить интервал изменения времени, начальные условия и точность решения. Для этого есть пункт меню Solve-Solve Parameters.

Затем производим триангуляцию. После проведения триангуляции и прежде чем запускать задачу на выполнение, обеспечим возможность увидеть колебания мембраны. Пункт меню Plot-Parameters откроет окно Plot Selection. Установим там настройки, в том числе включим переключатель Animation. Затем нажмем на кнопку Options и откроется окно Animation Options где укажем число кадров в секунду и число повторов. Нажатие на кнопку Plot запустит процесс.

Системы двух дифференциальных уравнений в частных производных решаются аналогично. Надо с помощью пункта меню Options-Application установить режим Generic System. Тогда появится возможность вводить коэффициенты сразу для двух уравнений.