Косвенные измерения

Физическая величина, значение которой необходимо определить опытным путем, не всегда может быть измерена непосредственно. Часто она является функцией других величин x₁, x₂, x₃. Измерения, при которых значение физической величины находят с помощью зависимости между ней и величинами, определенными путем прямых измерений, называются косвенными.

Физические эксперименты могут быть направлены на исследование характера самой зависимости между измеряемыми величинами. Если с помощью опытов необходимо определить функцию, связывающую измеряемые величины и заранее неизвестную, то процесс обработки результатов называют решением обратной задачи. Изучение общих методов решения таких задач выходит за рамки данного курса. Однако весьма распространенной является обратная задача, в которой нужно определить лишь некоторые параметры функциональной зависимости. Например, в случае прямолинейного равноускоренного движения материальной точки время t и ее координата x связаны зависимостью:

(1)

Хотя общий вид функции x(t) в данном случае известен (полином второй степени), ее параметры (x₀, v₀, a) могут оказаться неизвестными величинами. Задача обработки результатов в данном случае сводится к поиску параметров зависимости (x₀, v₀, a) по измеренным значениям входящих в нее величин (в данном случае координат точки, соответствующих фиксированным моментам времени).

В настоящей работе изложены правила обработка результатов косвенных измерений и некоторые методы решения обратных задач (графический метод, метод наименьших квадратов). Общая цель предлагаемых для выполнения лабораторных работ второго цикла курса "Физические измерения" (работы №7-12) - проиллюстрировать на конкретных примерах основные особенности косвенных измерений.

Оценка погрешности косвенных измерений

Условия задачи, решаемой при обработке результатов косвенных измерений, могут быть сформулированы следующим образом. Заданы:

1) - функциональная зависимость, связывающая физическую величину у с величинами x₁, x₂, x₃ значения которых определены путем прямых измерений;

2) значения величин x_i , определенные путем прямых измерений в виде: ;… ( средние значения измеряемых величин x -соответствующие полные погрешности их измерения).

Необходимо определить величину у, что предполагает оценку ее действительного (измеренного) значения y_изм погрешности измерений y

В качестве наилучшего приближения величины у принимают его, значение, получаемое при подстановке средних значений экспериментальных результатов в исходную функциональную зависимость:

Для определения погрешности косвенных измерений поступают следующим образом. Рассмотрим простейший случай, когда физическая величина у зависит только от одной переменкой . Тогда в соответствии с рис. 1 . где ,

Для оценки значений у₁ и y₂ заменим реальную функциональную зависимость линейной таким образом, чтобы прямая совпадала с касательной к графику функции в точке А с координатами (,y_изм.). Тогда параметр b , характеризующий наклон прямой , производной функции F(x) в точке А:

(2)

Если погрешность измерения величины х достаточно мала, прямая у на интервале отдо лишь незначительно отклоняется от кривой . Поэтому в качестве оценки величин y₁ и y₂ могут быть принять значения:

,

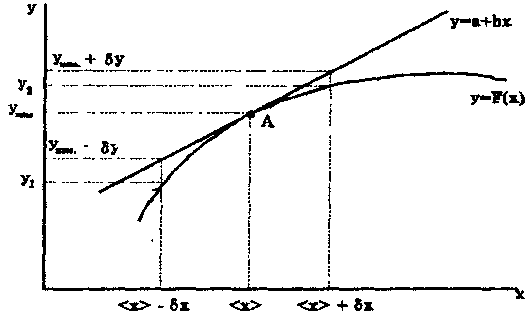
Рис. 1. Графическая оценка погрешности косвенных измерений

Таким образом, абсолютная погрешность определения величины у может быть оценена по формуле:

Например, если требуется определить объем шара измеренному его диаметру мм с помощью формулы

то оценка погрешности таких измерений в соответствии правилом (4) осуществляется следующим образом:

(мм)

Окончательный результат записывается в виде: мм

В общем случае функции нескольких переменных абсолютную погрешность косвенных измерений определяют, предположив, что процессы измерений величинx₁ ,x₂…x_N не влияют друг на друга, то есть процедура измерения величины x_i не искажает результатов измерений ни одной нз остальных N - 1 величин. Искомую погрешность оценивают как результат сложения не зависящих друг от друга погрешностей, каждая из которых совпадает с погрешностью определения величины y в условиях, когда все величины, x₁ ,x₂…x_N кроме одной (x_i) измерены абсолютно точно:

(5)

Производная в выражении (б) вычисляется от функции только по одной переменнойx_i в предположении, что все . другие N - 1 величин постоянны. Такая производная называется частной. Аналогично рассчитываются составляющие погрешности для всех остальных величин. Погрешность косвенных измерений величины у определяется по правилу сложения независимых случайных погрешностей (см.: Физические измерения. Ч. 1):

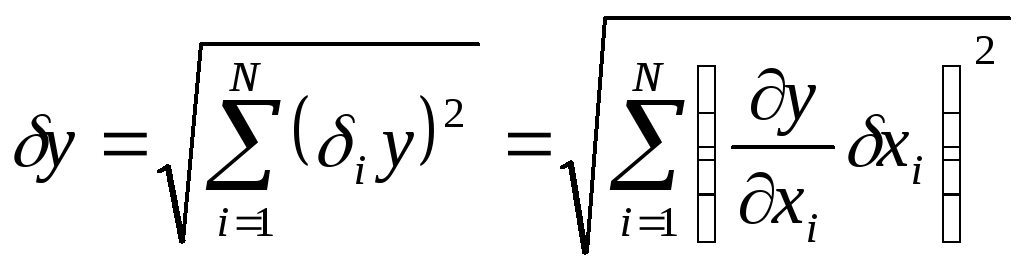(6)

Достаточно распространенной оказывается ситуация, в которой удобнее вычислять не абсолютную, а относительную погрешность косвенных измерений. В этом случае нужно дифференцировать не саму заданную функцию, а ее логарифм:

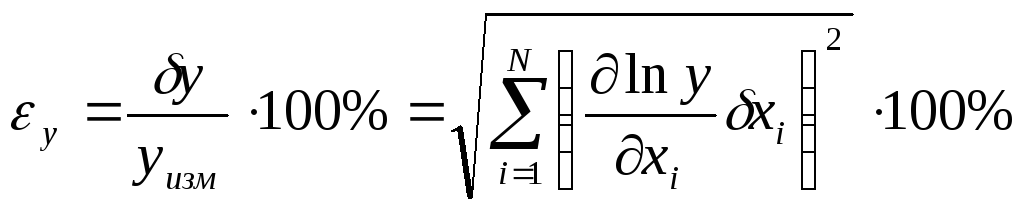(6а)

Следует подчеркнуть, что при использовании правила (6) или (6а) величина у лишь формально рассматривается в качестве функция непосредственно намеряемых величин. В случае его применения физический смысл соответствующего закона или уравнений, положенного в основу конкретных косвенных намерений, не принимается во внимание.

Например, в случае косвенных измерений сопротивления проводника методом амперметра и вольтметра (лабораторная работа №- 8) его величина определяется как отношение напряжения на проводнике к силе тока, текущего черва пего. На самом деле сопротивление проводника зависит от его геометрических размеров и свойств материала, из которого проводник изготовлен. Однако, чтобы оценить погрешность косвенных измерений сопротивления по известным значениям погрешностей измерений напряжения и тока, необходимо вычислить частные производные ,формально рассматривая сопротивление как функцию напряжения и тока:Пример Определите объем параллелепипеда, если измерены геометрические размеры его сторон: ,,

Решение

Объем параллелепипеда вычисляется как произведение его сторон:

Оценка наилучшего значения объема:

Частные производные от V по переменным a, b и с равны:

, ,

В случае вычисления относительной погрешности:

, ,

Абсолютная погрешность определения объема параллелепипеда в соответствия с правилом (6) определяется следующим образом:

В соответствии с правилом (6а) относительная погрешность определения объема параллелепипеда равна

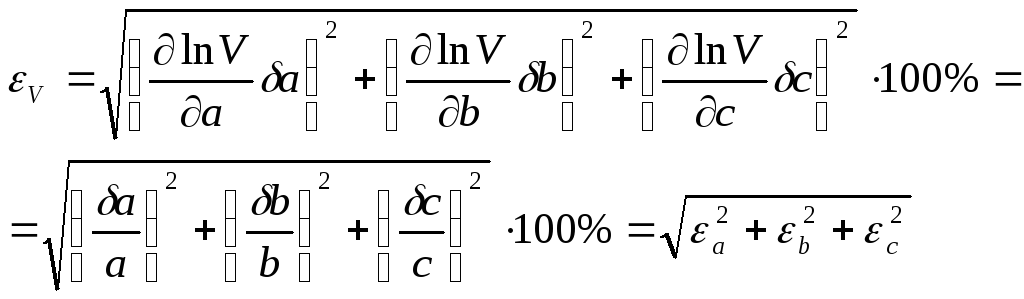
Рассмотренный пример показывает, что в случае, когда физическая величина определяется в результате перемножения непосредственно измеряемых величин, относительная погрешность косвенных измерений может быть вычислена как квадратный корень из суммы квадратов относительных погрешностей прямых измерений. Поэтому в данном случае значительно проще оценить относительную погрешность по правилу (6а) и лишь затем определить абсолютную погрешность.

Правила построения графиков

В случае исследования зависимости одной физической величины от другой (например, силы тока от напряжения, силы взаимодействия тел от расстояния между ними и т.п.) каждая из них измеряется независимым способом. Цель такого опыта заключается в изучении закона, определяющего характер связи между интересующими экспериментатора физическими величинами. Практически задача обработки результатов измерений сводится к проведению некоторой кривой по полученным экспериментальным точкам, нанесенным в соответствующей системе координат. Для решения этой задачи результаты измерений удобно представлять в виде графиков.

При построении графиков необходимо соблюдать следующее правила:

1. Все подученные экспериментальные результаты должны быть занесены в таблицу, в которой каждому значению одной величины соответствует определенное значение другой; пара значений двух величин задает координаты одной точки в выбранной системе координат. Для построения графиков используют миллиметровую бумагу.

3. Около осей графиков указывают соответствующие им физические величины и используемые единицы измерений (чаще всего применяется декартова прямоугольная система координат).

4. Масштаб на осях выбирают таким, чтобы экспериментальные точки располагались по всей площади графика, а минимальная цена деления масштаба была меньше абсолютной погрешности измерений.

5. Экспериментальные точки наносят на график с максимальной аккуратностью, а погрешности изображают в виде соответствующих интервалов 2δI, 2δU

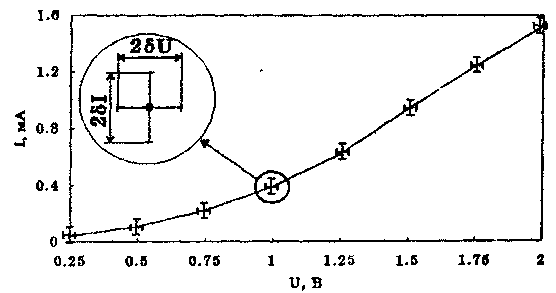
Рис. 2. Пример построения граф и экспериментальной зависимости

После того как на графике нанесены экспериментальные точки, их соединяют отрезками прямых или проводят кривую. В последнем случае, как правило, проводится простейшая кривая, отклонение экспериментальных точек от которой лежите в пределах погрешностей измерений. В случае экспериментальной проверки, какого либо закона часто график зависимости строк в тех координатах, в которых экспериментальные точки должны быть расположены вдоль прямой. Если в -том случае можно провести такую прямую, от которой точки отклоняются не более чем на погрешность измерений, то можно сделать вывод, что проверяемый: закон действительно справедлив с точностью до погрешностей измерений. Параметры прямой несут при этом дополнительную информацию о свойствах изучаемого объекта. Для их количественного определения используют два общепринятых метода: графический и метод наименьших квадратов (МНК).

Графический метод построения прямой по экспериментальным точкам

Пусть две физические величины x и у связаны линейной зависимостью вида . В результате экспериментальных исследований определены пары соответствующих друг другу значений переменных (x_i, y_i) и оценены погрешности их измерений δx_i, δy_i , полученные экспериментальные точки нанесены на координатную плоскость (x, y) (рис.3).

При наличии случайной погрешности точки на графике всегда имеют некоторый разброс, поэтому невозможно найти такую прямую, которая проходила бы через все экспериментальные точки. С геометрической точки зрения задача обработки результатов измерений в данном случае сводится к замене ломаной линии прямой, наиболее близкой к ней в соответствии с некоторым критерием. Этот прием называется сглаживанием экспериментальных результатов. Графический метод заключается в том, что прямую проводят, руководствуясь двумя правилами:

1. Экспериментальные точки не должны отступать от прямой на расстояние, превышающее абсолютную погрешность измерений.

2. При проведении прямой необходимо следить за тем, чтобы на каждом достаточно большом ее участке экспериментальные точки располагались как выше, так и ниже прямой. Рекомендуется стремиться к такому положению прямой, когда количество точек, оказавшихся над прямой и под прямой, было примерно одинаковы на всех участках зависимости.

После того, как прямая проведена (для этого удобно воспользоваться прозрачной линейкой), возможно определение параметров: коэффициент b равен тангенсу угла наклона прямой (), а параметр а равен значению функции при х = 0.

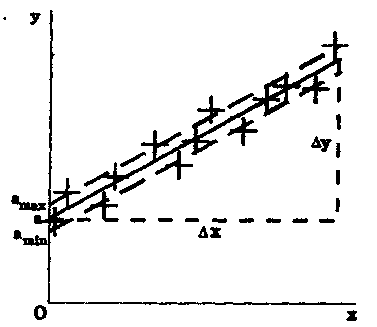
Рис. 3. Построение прямой по экспериментальным точкам графическим методом и оценка погрешности определения параметра а

Чтобы найти погрешность в определении параметра a, необходимо смещать прямую вниз параллельно самой себе до тех пор, пока выше нее не окажется вдвое больше экспериментальных точек, чем ниже (см. рис. 3). Такое положение прямой соответствует значению a, равному a_min Затем следует смещать прямую вверх до тех пор, пока снизу не окажется вдвое больше точек, чем сверху. Полученное положение прямой дает возможность определить a_max Погрешность определения параметра а оценивают с помощью формулы:

(7)

где N - число экспериментальных точек на графике.

Погрешность в определении параметра b оценивают следующим образом. Отрезок оси Ох, на "котором размещены экспериментальные точки, разбивают на три равные части (рис.4). Затем проведенная ранее прямая поворачивается относительно центра графика так, чтобы на правом участке выше нее оказалось вдвое больше точек, чем под ней, а на левом наоборот. Данное положение соответствует b=b_mi. Аналогичным путем проводится прямая с . Искомая погрешность определяется по формуле:

(8)

Из формул (7) и (8) следует, что погрешности δa и δb уменьшается при увеличении числа экспериментальных точек.

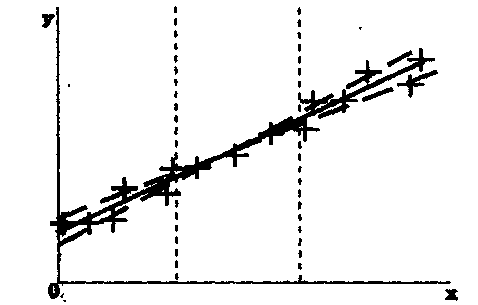
Рис. 4. Оценка погрешности определения коэффициента b при построении прямой графическим методом

Метод наименьших квадратов

Результаты, полученные в предыдущем разделе путем проведения прямой черев экспериментальные точки "на глаз", достаточно субъективны. Они зависят от квалификации и личных качеств экспериментатора. Параметры наилучшей прямой можно определить более . объективным способом (аналитически), используя метод наименьших квадратов (метод Лежандра, 1809.).

Лежандр предложил критерий выбора параметров a, b наилучшей прямой: сумма квадратов отклонения результатов измерений физической величины y от этой прямой должна быть наименьшей. Отклонение ординаты точки прямой от результата i - го измерения величины у равно разности (рис.3). Поэтому критерий Лежандра сводится к требованию:

(9)

Необходимым условием минимума величины Ф как функции параметров прямой а, b является одновременное равенство нулю обеих ее частных производных:

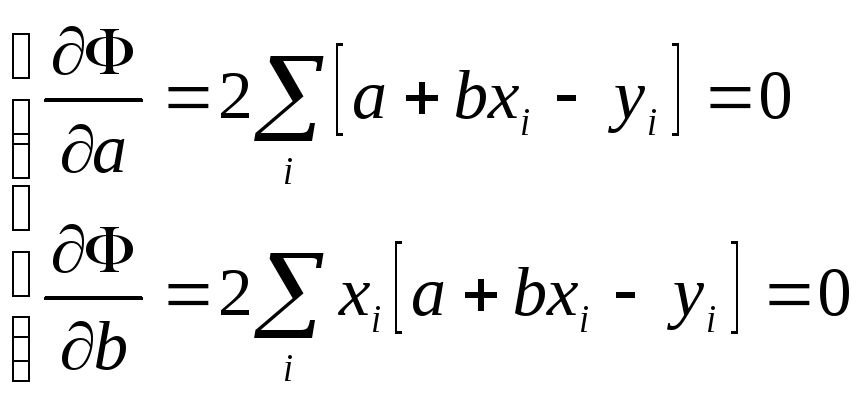(10)

Решение полученной системы уравнений относительно неизвестных величин а, b имеет вид:

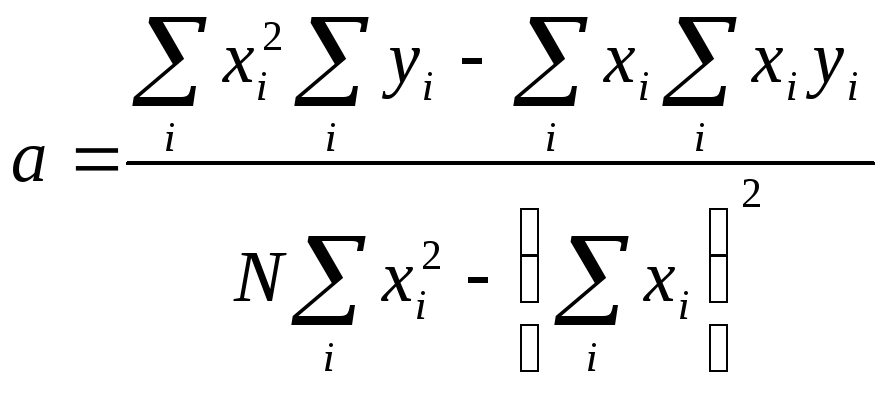(11)

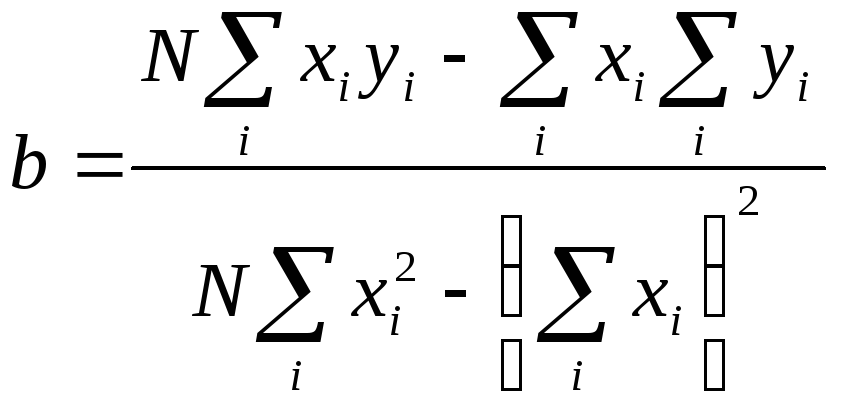(12)

Погрешности их оценки находятся при этом по формулам:

(13)

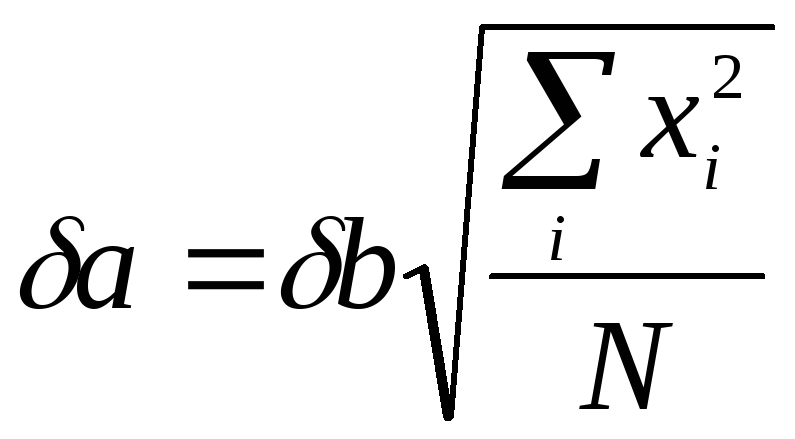(14)

В случав, когда a = 0 (прямая проходит черев начало координат), выражения (12), (14) преобразуются к виду

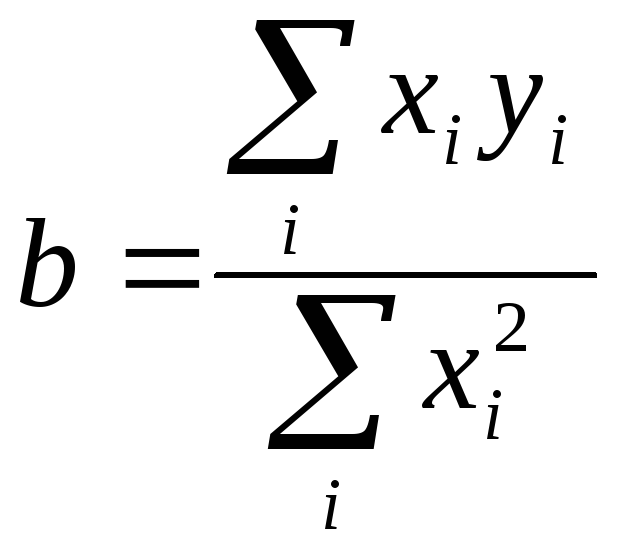(15)

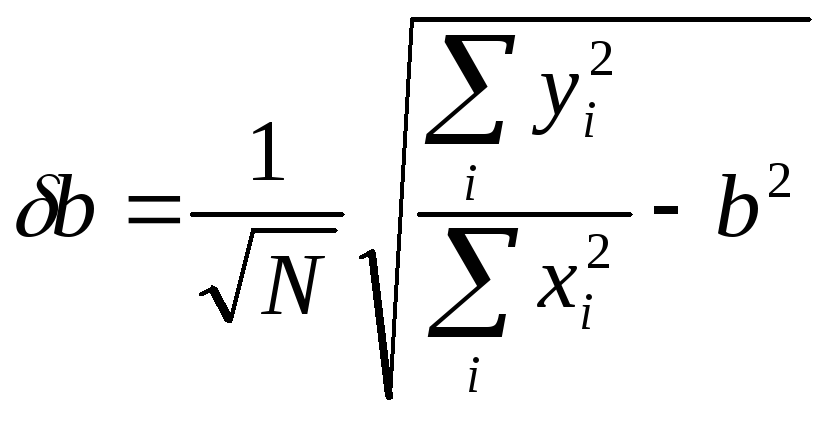(16)

Перед проведением расчетов по методу наименьших квадратов рекомендуется нанести экспериментальные точки на координатную плоскость. После того как расчеты будут выполнены, нужно провести прямую в соответствии с полученными значениями ее параметров и убедиться, что она проходит достаточно близко к экспериментальным точкам.

Следует помнить, что параметры прямой либо сами являются физическими величинами, с целью определения значений которых проводится эксперимент, либо связаны с такими величинами. В качестве примеров применения метода наименьших квадратов данная часть курса "Физические намерения" включает лабораторные работы № 11, 12.

Метод наименьших квадратов может быть использован не только для построения прямой по экспериментальным точкам, но и в случаях исследования более сложных функциональных зависимостей. Его применение эффективно в ситуациях, когда исследуемая функция линейно зависит от неизвестных параметров. Например, параметры зависимости координаты точки от времени в случае ее равноускоренного движения также могут быть определены с помощью этого метода, если известно несколько пар одновременно измеренных переменных