
C22013
.pdf
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
МАТЕМАТИКА. ЕГЭ 2013
Многогранники:
типы задач и методы их решения
(типовые задания С2)
Прокофьев А.А. |
Корянов А.Г. |
Прокофьев А.А. – доктор педагогических наук, заведующий кафедрой высшей математики №1 НИУ МИЭТ, учитель математики ГОУ лицей №1557 г. Зеленограда; e-mail: aaprokof@yandex.ru
Корянов А.Г. – методист по математике городского информационнометодического Центра (МБОУ БГИМЦ) г. Брянска, учитель математики МОУ лицей №27 г. Брянска; e-mail: akoryanov@mail.ru
СОДЕРЖАНИЕ |
стр. |
|
|
Введение |
2 |
Глава 1. Расстояния и углы |
3 |
1.1. Расстояние между двумя точками |
3 |
Тренировочные упражнения…….. |
4 |
1.2.Расстояние от точки до прямой…. 5 Тренировочные упражнения…….. 9
1.3.Расстояние от точки до плоскости 10 Тренировочные упражнения…….. 19
1.4.Расстояние между скрещивающимися прямыми…………………….. 20 Тренировочные упражнения…….. 27
1.5.Угол между двумя прямыми......... 28 Тренировочные упражнения…….. 33
1.6.Угол между прямой и плоско-
стью…………………………………… 35
Тренировочные упражнения…….. 41
1.7. Угол между плоскостями |
43 |
Тренировочные упражнения…….. |
59 |
Глава 2. Площади и объемы……….. 62
2.1. Площадь поверхности много-
гранника ………………………………. 62
04.12.2012 |
1 |
2.2.Площадь сечения многогранника 65
2.3.Объем многогранника…………… 69
Тренировочные упражнения…….. 81
Глава 3. Дополнения……………… 83
3.1.Методы построение сечения многогранника плоскостью...……………. 83
3.2.Векторный метод………………… 88
3.3.Координатный метод…………….. 90
3.4.Опорные задачи………………….. 93
Ответы и указания……………………100
Список и источники литературы…...101
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Введение
Задачи части «С» Единого государственного экзамена по стереометрии в последнее время большей частью посвящены вычислению расстояний и углов в пространстве.
Около 30 % выпускников приступало к решению задачи С2 на ЕГЭ 2010-2012 гг. Так в 2010 году процент приступивших к выполнению составил 30%, в 2011 году –
33,1%, а в 2012 году – 29%.
Задание С2 оценивается в 2 балла. В 2010 году от 1 до 2 баллов за задачу С2 смогли получить 11,6% участников экзамена, в 2011 – 13,9%, а в 2012 – 5,53%.
Полное решение каждой задачи состоит из теоретической части, заключающейся в обосновании взаимного расположения элементов заданной стереометрической конфигурации, и вычислительной части. При проверке задачи С2 выставление баллов производится в соответствии со следующими критериями.
Содержание критерия |
Баллы |
|
Обоснованно получен правиль- |
2 |
|
ный ответ |
||
|
||
Решение содержит обоснован- |
|
|
ный переход к планиметриче- |
|
|
ской задаче, но получен невер- |
1 |
|
ный ответ или решение не за- |
||
кончено, или при правильном |
|
|
ответе решение недостаточно |
|
|
обосновано. |
|
|
Решение не соответствует ни |
0 |
|
одному из критериев, перечис- |
||
ленных выше |
|
|
Максимальный балл |
2 |
В первой главе «Расстояния и углы» представлены разные методы решения задач типа С2. Геометрические методы решения задачи опираются на определения расстояния или угла, и требуют от учащихся развитого пространственного воображения. Кроме этого подхода в пособии рассмотрены координатный и векторный методы, которые могут быть эффективно использованы при решении задач разного вида. Применение опорных задач также может привести к рациональному решению задачи.
04.12.2012 |
2 |
Следует отметить, что при решении задачи координатным или векторным методами выпускник должен получить правильный ответ, и только тогда его решение будет оценено в 2 балла. В противном случае его решение не соответствует приведенным критериям и будет оценено
в0 баллов.
Вкодификатор элементов содержания к уровню подготовки выпускников входят разделы, связанные с темой «Многогранники», которые отражены в данном пособии: сечения куба, призмы, пирамиды; боковая поверхность призмы, пирамиды; объем куба, прямоугольного параллелепипеда, пирамиды, призмы. Во второй главе «Площади и объемы» представлены методы решения стереометрических задач на многогранниках с использованием формул их площади поверхности и объема.
Втретьей главе «Дополнения» собран основной материал, который используется при решении многих стереометрических задач, владение которым подразумевается. В частности, представлены основные способы построения сечений многогранников плоскостью, основные способы введения систем координат для использования координатного метода, дано представление о векторном методе решения задач. В решениях многих задач, приведенных в данном пособии, имеются ссылки на опорные задачи, полный набор которых помещен в пункте 3.4 на стр. 9399.
Авторы надеются, что данное пособие будет полезно учащимся при их подготовке к итоговому экзамену.
Желаем успеха!
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Глава 1. Расстояния и углы
Тема «Расстояния и углы» является основой для других разделов стереометрии. В данном разделе представлено взаимное расположение точек, прямых и плоскостей на многогранниках, рассмотрены основные виды задач и методы их решения.
1.1. Расстояние между двумя точками
Расстояние между точками A и B можно вычислить:
1) как длину отрезка AB , если отрезок AB удается включить в некоторый треугольник в качестве одной из его сторон;
2) по формуле
A,B 
 (x2 x1)2 (y2 y1)2 (z2 z1)2 , (1)
(x2 x1)2 (y2 y1)2 (z2 z1)2 , (1)
где A(x1, y1, z1), B(x2, y2, z2);
3) по формуле
|
|
|
|
|
|
|
|
AB |
|
AB AB |
AB |
|
a2 b2 c2 , (2) |
||
|
|
|
|
|
|
|
|
где {a, b, c} – координаты вектора AB в декартовой системе координат.
Поэтапно-вычислительный метод
Пример 1. В единичном кубе
ABCDA1B1C1D1 |
на диагоналях граней |
||||||||
AD1 |
и D1B1 |
взяты точки Е и F так, что |
|||||||
D E |
1 |
AD , D F |
2 |
D B . Найти длину |
|||||
|
|
||||||||
1 |
3 |
1 |
1 |
3 |
|
1 |
1 |
||
отрезка EF. |
|
|
|
|
|
|
|||
|
|
|
|
|
B1 |
|
|
||
|
|
|
A1 |
|
|
F |
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
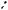
 E
E D1
D1


 B
B 


A




 C
C
D
Рис. 1
Решение. Длину отрезка EF найдем по теореме косинусов из треугольника D1EF (см. рис. 1), в котором
D F |
2 |
|
|
, |
D E |
1 |
|
|
, |
FD E |
|
|
|
2 |
2 |
||||||||||
|
|
|
|
|||||||||
1 |
3 |
|
|
|
1 |
3 |
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
04.12.2012 |
|
|
|
|
|
|
|
|
3 |
|||
(треугольник AB1D1 является равносторонним). Имеем
EF2 D E2 |
|
D F2 2D E D F cos |
|
|
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
8 |
2 |
|
2 |
|
|
2 |
2 |
|
|
1 |
|
2 |
, |
|
|
|
|
|
|
|||||
|
9 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
9 |
|
|
|
|
|
3 |
2 |
3 |
|
|
|
|
|
|
|
||||||||||||
откуда EF |
|
|
6 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
6 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Координатный метод
Приступая к решению задач этим методом полезно разобрать задачу №1 из списка опорных задач (см. главу 3 п. 3.4).
Пусть |
точки |
|
A(x1; y1; z1) |
и |
||||||||
B(x2; y2; z2) |
– концы отрезка AB . Тогда |
|||||||||||
внутренняя точка C отрезка AB такая, |
||||||||||||
что |
|
AC:CB k , |
имеет |
|
|
координаты |
||||||
x k x |
y k y |
|
z k z |
2 |
|
|
||||||
C |
|
1 |
2 |
; |
1 |
2 |
; |
1 |
|
. |
|
|
|
|
|
k 1 |
|
|
|
|
|||||
|
k 1 |
|
k 1 |
|
||||||||
Пример 2. В единичном кубе |
||||||||||||
ABCDA1B1C1D1 |
точки E и K – середины |
|||||||||||
ребер |
AA1 |
и CD соответственно, а |
||||||||||
точка |
M |
расположена |
на диагонали |
|||||||||
B1D1 так, что B1M 2MD1. Найти расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МK такая, что ML 2LK.
Решение. Введем прямоугольную систему координат, как указано на рисунке 2.
z |
B1 |
|
|
|
|
|
|
|
|
||
A1 |
|
|
|
|
M |
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Q |
|
y |
D1 |
|
|
|
|
|||
E |
B |
|
|
L |
C |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
D |
|
|
|
|
|||
|
|
|
|
|
|
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
||
|
1 |
|
|
|
1 |
|
|
|
|
||
Тогда Е 0;0; |
|
|
|
, K 1; |
|
;0 |
|
, |
В (0;1;1), |
||
|
2 |
|
|
|
2 |
|
|
|
1 |
||
D1(1;0;1). Для нахождения координат точки М используем формулу координат
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
точки (опорная задача 1), делящей отре-
зок B1D1 в отношении 2:1. Имеем |
|
|||||||||||
0 2 1 1 2 0 1 2 1 |
|
2 1 |
|
|
||||||||
М |
|
, |
|
, |
|
|
|
|
, |
|
|
,1 . |
|
|
|
|
|
||||||||
|
1 2 |
1 2 |
1 2 |
3 3 |
|
|||||||
Аналогично получим координаты точки L, делящей отрезок MK в отношении 2:1. Имеем
|
2 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 1 |
|
|
|
2 |
|
|
|
1 2 0 |
|
|
8 4 1 |
|
||||||
|
|
3 |
|
|||||||||||||||||
L |
3 |
|
; |
2 |
; |
|
|
|
|
; |
|
; |
|
. |
||||||
|
|
|
|
|
|
|
||||||||||||||
1 2 |
|
|
|
1 2 |
1 2 |
9 9 3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Координаты точки Q равны полусуммам соответствующих координат точек E и
|
1 |
|
1 |
|
3 |
|
|
М, поэтому Q |
|
; |
|
; |
|
|
. Применим фор- |
|
6 |
4 |
|||||
3 |
|
|
|
||||
мулу (1) для расстояния между точками с заданными координатами
LQ |
|
|
|
|
1 |
|
|
|
8 2 |
|
|
1 |
|
|
|
|
|
4 |
2 |
|
|
3 |
|
|
|
1 |
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
9 |
|
6 |
|
|
|
|
|
9 |
|
|
|
|
4 |
|
|
|
3 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
725 |
|
|
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
362 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
29 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Векторный метод |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Пример 3. В единичном кубе |
||||||||||||||||||||||||||||||||||||||||||||||||
ABCDA1B1C1D1 |
на |
|
|
|
диагоналях |
|
граней |
|||||||||||||||||||||||||||||||||||||||||||
AD1 и D1B1 |
взяты точки E и F так, что |
|||||||||||||||||||||||||||||||||||||||||||||||||
D E |
1 |
AD , |
D F |
2 |
D B . Найти длину |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
3 |
|
|
|
1 |
|
|
|
1 |
|
|
3 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
отрезка EF. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Решение. Пусть AD a, |
|
|
|
|
|
|
|
|
|
AA1 c |
|||||||||||||||||||||||||||||||||||||||
|
AB b, |
|||||||||||||||||||||||||||||||||||||||||||||||||
(см. рис. 1), |
тогда |
|
|a| |b | |c | 1, |
|||||||||||||||||||||||||||||||||||||||||||||||
a b a c b c 0. |
|
|
|
|
Выразим |
|
вектор |
|||||||||||||||||||||||||||||||||||||||||||
FE через базисные векторы a, |
|
|
b, |
|
c : |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
FE EA AB B F |
2 |
(a c) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
(b |
c) |
|
|
|
(a b) |
|
|
a |
|
|
|
|
b |
|
|
|
|
c . |
|||||||||||||||||||||||||||||||
|
|
3 |
3 |
3 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Тогда по формуле (2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
FE |
|
FE |
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
c |
|
||||||||||||||||||||||||||||||
|
|
3 |
|
3 |
|
3 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 2 |
|
|
4 2 |
|
|
1 2 |
|
|
4 |
|
|
2 |
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
c |
|
|
a b |
|
|
b |
c |
|
|
|
a |
c |
|||||||||||||||
9 |
9 |
|
|
|
9 |
9 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
4 |
|
1 |
|
|
|
|
6 |
|
. |
|
|
|
|
Ответ: |
|
|
6 |
|
. |
|||||||||||||||||
|
9 |
|
9 |
9 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||
|
Замечание. |
Вектор |
FE в данном ба- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
1 |
|
|
|
|
|
|
|||||||
зисе имеет координаты |
|
|
|
; |
|
; |
|
|
, |
|
по- |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
3 |
|
|
|
|
|
|
||||||||
этому его длину можно найти по форму-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ле |
AB |
|
|
a2 b2 c2 , то есть |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
AB |
|
|
1 |
|
4 |
|
1 |
|
|
6 |
|||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
9 |
9 |
9 |
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Тренировочные упражнения
1.Ребра правильной четырехугольной призмы равны 1, 4 и 4. Найдите расстояние от вершины до центра основания призмы, не содержащего эту вершину.
2.В единичном кубе ABCDA1B1C1D1
точки E , K и L – середины ребер AA1,
CD и B1C1 соответственно, а точки M и
N расположены |
соответственно |
на от- |
резках EK |
и LK так, |
что |
EM :MK 2:3, а |
LN : NK 1:4 . |
Найди- |
те длину отрезка МN.
3. В правильной треугольной призме ABCA1B1C1 на ребрах AB и B1C1 выбраны точки E и K соответственно так, что AE : EB 1:2, а B1K :KC1 5:1. Найдите длину отрезка EK, сторона основания призмы равна 6, а боковое ребро равно 2.
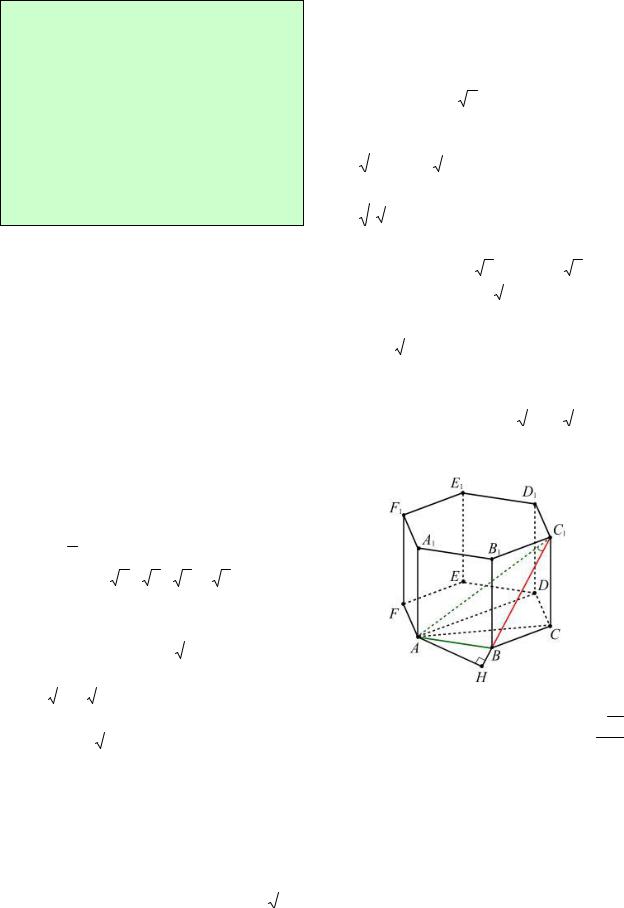
4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все ребра которой равны 2, найдите расстояние от точки A до точек: а) C1 ; б) D1 ; в) M, где M центр грани EE1D1D.
5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все ребра которой равны 1, найдите расстояние между точками A и E1.
6. В правильной четырехугольной пирамиде SABCD , сторона основания и бо-
ковое ребро которой равны 4
 2 и 5 соответственно. Найдите расстояние между точками E и K, если известно, что Е лежит на боковом ребре SB и SE 2BE, а K
2 и 5 соответственно. Найдите расстояние между точками E и K, если известно, что Е лежит на боковом ребре SB и SE 2BE, а K
– на стороне основания AD и AK 3KD.
04.12.2012 |
4 |
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
1.2.Расстояние от точки до прямой
Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
Расстояние между двумя параллель-
ными прямыми равно длине отрезка их общего перпендикуляра.
Расстояние между двумя параллель-
ными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
Поэтапно-вычислительный метод
Расстояние от точки M до прямой AB , обозначаемое (M; AB), вычисляют, как длину высоты, опущенной из точки M на основание AB (или ее продолжение) треугольника ABM .
Пример 4. При условиях примера 1 найти расстояние от точки D1 до прямой EF.
Решение. Пусть h – длина высоты треугольника D1EF, опущенной из точки
D1. Найдем h, используя метод площа-
дей. Площадь треугольника D1EF равна
1
2 D1F D1E sin FD1E
|
|
|
|
|
|
1 |
|
|
2 2 |
|
|
2 |
|
3 |
|
|
|
3 |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
3 |
3 |
|
2 |
9 |
|
|
|
|
|
|
||||||||||||||||||||||||
С другой стороны площадь треугольника |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
h. Из уравне- |
||||||||||||||||||||
D EF |
|
равна |
|
FE h |
|
|
6 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ния |
|
|
3 |
|
|
|
|
|
6 |
|
h |
|
находим |
|
|
|
искомое |
|
рас- |
||||||||||||||||||
|
9 |
|
|
6 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
стояние h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Замечание. Можно заметить, что вы- |
|||||||||||||||||||||||||||||||||||||
полняется равенство FE2 |
D E2 D F2 , |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|||||
т.е. треугольник D1EF прямоугольный и |
|||||||||||||||||||||||||||||||||||||
длина |
|
отрезка |
D1E |
|
является искомым |
||||||||||||||||||||||||||||||||
расстоянием. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
04.12.2012 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|||||||||
Пример 5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки A до прямой BC1.
Решение. В квадрате BCC1B1 диаго-
наль BC1 |
равна 2 (см. рис. 3). В прямо- |
|||||||||
угольном |
|
треугольнике ACD, |
где |
|||||||
ACD 90 , |
|
|
AD 2, |
находим |
AC |
|||||
|
|
|
|
|
|
|
|
|
||
22 12 |
|
|
|
|
. Из прямоугольного тре- |
|||||
|
|
3 |
||||||||
угольника |
|
ACC1 |
имеем |
AC1 |
||||||
|
|
|
|
ABC , |
||||||
( |
|
|
|
|
2. В треугольнике |
|||||
3)2 12 |
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
используя теорему косинусов, получаем
|
|
|
|
|
22 ( 2) |
2 12 |
5 2 |
|
|
|
|||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
, |
||||||||||
|
|
|
|
|
|
|
8 |
||||||||||||||
2 2 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
AC1B . |
|
Далее |
|
|
|
находим |
||||||||||||||
|
|
|
|
и из треугольника AC H вы- |
|||||||||||||||||
sin |
|
14 |
|||||||||||||||||||
|
|
|
|||||||||||||||||||
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
соту |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
AH AC sin 2 |
|
|
|
|
|
|
|
|
. |
||||||||||||
14 |
|
14 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
8 |
|
|
|
|
|
4 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 3
Ответ: 
 14 . 4
14 . 4
Пример 6. (МИОО, 2010). В тетра-
эдре ABCD, все ребра которого равны 1, найти расстояние от точки A до прямой, проходящей через точку B и середину E ребра CD.
Решение. Так как все ребра ABCD равные правильные треугольники, то медианы BE и AE треугольников BDC и
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
ADC (см. рис. 4) равны и BE AE 3. 2
Рассмотрим равнобедренный треугольник BEA и его высоты EM и AH. Выражая площадь треугольника BEA двумя способами, получаем
S |
BEA |
|
1 |
AH BE |
1 |
EM AB, |
|
|
|
||||||
|
2 |
|
2 |
|
|||
получаем |
равенство |
AH BE EM AB. |
|||||
D
E
H


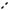
 C
C
B
M

A
|
|
Рис. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
2 |
|||||||||||||
EM |
BE2 BM 2 |
||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
||||||||||||||
то получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
EM AB |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
. |
|||||||||||||
AH |
|
|
|
2 |
6 |
||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
BE |
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
||||||||||||
Ответ: 6 . 3
В некоторых задачах удобно использовать плоскость, проходящую через данную точку перпендикулярно данной прямой.
Пример 7. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки D до прямой A1C.
Решение. Пусть A1C BDC1 F (рис. 5). Так как A1C BDC1 (опорная задача
20), то FC1 FB FD как проекции на плоскость BDC1 равных наклонных CC1 , СВ и CD соответственно. Следовательно, точка F является центром правильного треугольника BDC1 . Поэтому искомое расстояние равно радиусу окружности,
04.12.2012 |
6 |
описанной около треугольника BDC1 .
Сторона этого треугольника равна 
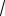 2 , значит,
2 , значит,
(D, AC) DF |
2 3 |
|
6 |
. |
|
|
|
||||
1 |
3 |
3 |
|
||
|
|
||||
B1 |
|
|
|
|
|
A1 |
|
C1 |
|||
D1 |
|||||
|
|
|
|||
B |
F |
|
|
|
|
A |
|
C |
|||
D |
|
|
|
|
|
Рис. 5 |
|
|
|
||
Ответ: 6 . 3
Метод параллельных прямых
Данный метод основан на использовании следующего утверждения: расстояние от точки M до прямой a равно расстоянию до прямой a от произвольной точки P , лежащей на прямой b , проходящей через точку M и параллельной прямой a.
Этот метод удобен в применении, когда искомый перпендикуляр выходит за пределы многогранника. В этом случае его можно заменить перпендикуляром, расположенным внутри многогранника, либо перпендикуляром, длина отрезка которого известна.
Решим указанным методом пример 5. Решение. В квадрате BCC1B1 диаго-
наль BC1 равна 
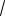 2 (см. рис. 6). Пусть O
2 (см. рис. 6). Пусть O
и O1 – центры нижнего и верхнего осно-
ваний соответственно. Так как AB ||O1C1
и AB O1C1 , то ABC1O1 – параллело-
грамм. Отсюда AO1 ||BC1 , поэтому рас-
стояние (A;BC1) (O1;BC1). Из прямоугольного треугольника BOO1 нахо-
дим BO1 
 2 .
2 .
В треугольнике BO1C1 , используя теорему косинусов, получаем
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
cos 12 (
 2)2 (
2)2 (
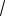 2)2
2)2 
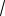 2 ,
2 ,
|
|
2 1 2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||
где O C B. Находим |
sin |
|
|
|
|
14 |
|
|
и |
||||||||||
|
|
|
|
|
|
|
|||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||
из треугольника O1C1H высоту |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||
O H O C sin 1 |
|
14 |
14 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
1 |
1 |
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
E1 |
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
O1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
||||
|
A1 |
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F |
|
O |
D |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
||
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||
|
|
|
|
Ответ: |
14 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4
Координатный и векторный методы
Как уже было отмечено выше расстояние между точками A и B можно вычислить по формулам (1) и (2) (см. стр. 3).
Рассмотрим векторный подход к решению задач данного вида. Пусть дана прямая l с направляющим вектором q, точка A лежит на прямой l, точка M
вне прямой l, MA m (см. рис. 7).
Чтобы найти расстояние от точки M до прямой l, т.е. длину перпендикуляра
MP |
(P l ), представим |
вектор MP в |
виде |
|
|
MP MA AP m x q . |
||
M
m
q
l |
A |
P |
Рис. 7
Неизвестный коэффициент x находится из условия перпендикулярности
вектора MP вектору q:
|
|
|
MP q |
0 (m x q) q 0. |
|
Искомое расстояние выражается следующим образом:
MP 
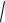 (m x q)2 .
(m x q)2 .
Координатный метод
Пример 8. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки D1 до прямой РQ, где Р и Q – сере-
дины соответственно ребер A1B1 и ВС.
Решение. Рассмотрим прямоугольную систему координат с началом в точке A (см. рис. 8). Найдем координаты точек
|
|
1 |
|
1 |
|
|
|
|
||
P |
0; |
|
;1 |
, Q |
|
;1; 0 |
|
, |
D (1;0;1). |
|
2 |
2 |
|||||||||
|
|
|
|
|
|
|
1 |
|||
z
|
|
|
D1 |
|
|
|
|
|
A1 P |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
B1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
A C1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|||||
|
x |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
y |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Рис. 8 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||
|
|
|
PQ |
1 |
|
|
1 |
1 |
|
3 |
|
|
|
|
|
|
||||||||||
|
4 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
. |
|||||||||||
DQ |
|
1 |
1 1 |
|
, |
D P 1 |
1 |
0 |
|
5 |
|
|||||||||||||||
4 |
|
2 |
|
|
||||||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
4 |
|
4 |
|
|
||||||||||||
Из треугольника D1PQ , используя |
||||||||||||||||||||||||||
формулу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
cos D PQ |
|
D P2 QP2 |
DQ2 |
, |
|
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
2 D1P QP |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
находим
04.12.2012 |
7 |
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
|
|
|
|
|
|
|
|
|
5 |
|
|
3 |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
cos D PQ |
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
3 |
|
|
|
|
30 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Далее получаем |
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
29 |
|
|
||||||||||||||||||
sin D PQ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
30 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пусть D1N PQ , где N PQ . Тогда |
|||||||||||||||||||||||||||||||||||||||||
D1N D1P sin D1PQ, |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||
D N |
|
5 |
|
|
29 |
|
|
|
|
|
|
174 |
|
174 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 |
4 |
|
|
|
30 |
|
|
|
|
|
|
|
|
144 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Ответ: 
 174 . 12
174 . 12
Векторный метод
Пример 9. В треугольной пирамиде ABCD при вершине D все плоские углы
равны , AD 2, BD 4, CD 3. Точки
3
P , M и K являются серединами ребер AD, BD и BC соответственно. Найти расстояние от точки M до прямой PK .
Решение. |
Пусть |
DA a, |
|
|
|||||
DB b , |
|||||||||
DC c |
(см. |
рис. |
9). |
Тогда имеем сле- |
|||||
дующую |
таблицу |
умножения |
векторов |
||||||
базиса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
c |
|
|
|
a |
4 |
|
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
4 |
|
|
16 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
3 |
|
|
6 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
Если MH PK , где H PK (см. рис. 9),
то в силу коллинеарности векторов PH и PK получаем PH x PK . Выразим век-
тор PK через базисные векторы a, |
b и |
|||||||||
c , используя правило многоугольника |
||||||||||
|
|
|
1 |
|
|
1 |
|
1 |
||
PK PD DM MK |
|
a |
|
|
b |
|
c , |
|||
2 |
2 |
2 |
||||||||
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
значит, PH |
x( a b c). |
Теперь вы- |
||||||||
|
||||||||||
2
разим вектор MH :
04.12.2012
MH MP PH DP DM PH
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
a |
|
b |
|
x( a b |
c). |
||
2 |
2 |
2 |
|||||||
|
|
|
|
|
|
||||
 D
D
M






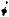 P
P

 H
H



 A
A
B
K 
 C
C
Рис. 9
Из условия перпендикулярности векторов
MH и PK имеем MH PK 0 или
((1 x)a (x 1)b xc)( a b c) 0.
Используя таблицу умножения базисных векторов, получаем уравнение
(1 x)( 4 4 3 4 16 6)
x( 3 6 9) 0,
откуда x 5.
|
|
|
|
9 |
1 |
|
1 |
|
|
|
|
1 |
|
5 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Тогда MH |
|
|
|
|
a |
|
|
b |
|
|
|
|
|
( a b |
c) |
||||||||||||
2 |
2 |
|
2 |
9 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
5 |
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
a |
|
|
|
|
b |
|
|
|
c |
|
|
|
|
(4a 4b 5c). |
|||||||||||
9 |
9 |
|
|
|
18 |
|
|||||||||||||||||||||
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
MP |
|
|
(4a 4b 5c)2 |
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

 16 4 16 16 25 9 32 4 40 3 40 6 18
16 4 16 16 25 9 32 4 40 3 40 6 18
297 11 . 324 12
Ответ: 11 . 12
Пример 10. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки D1 до прямой РQ, где Р и Q – сере-
дины соответственно ребер A1B1 и ВС.
Решение. |
Пусть |
AD a , |
AB b , |
AA1 c (см. |
рис. 8), |
тогда |a | |b | |
|
|c | 1, a b a c b c 0.
8
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Выразим вектор PQ через базисные
векторы a, b, c :
PQ PB1 B1B BQ
1b c 1 a 1 a 1b c , 2 2 2 2
|
|
|
|
|
|
|
|
|
|
|
|
PD a |
1 |
b. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть D1N PQ , |
|
|
|
|
|
N PQ . Выра- |
|||||||||||||||||||||||||||||||||||
где |
|||||||||||||||||||||||||||||||||||||||||
зим вектор D1N , учитывая коллинеар- |
|||||||||||||||||||||||||||||||||||||||||
ность векторов PN и PQ: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
D1N PN PD1 x PQ PD1 . |
|
||||||||||||||||||||||||||||||||||||||
Так |
как D1N PQ, |
то |
|
D1N PQ 0. |
|||||||||||||||||||||||||||||||||||||
Отсюда получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
(x PQ PD1) PQ 0, |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
PD1 |
PQ, |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x PQ |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
1 1 |
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
||||||||||||||||||||||
x |
|
a |
|
|
|
|
b c |
|
|
a |
|
|
|
|
b |
|
|
|
|
a |
|
|
|
b |
c , |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
||||||||||||
|
|
|
х |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
, |
|
х |
|
|
. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
6 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
D N |
1 |
PQ PD |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
b c |
|
|
|
|
|
b a |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
6 2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
11a 7 b 1c . 12 12 6
Длина вектора
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
7 |
|
|
1 |
2 |
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
D1N |
D1N |
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
c |
|
|||||||||||
12 |
|
12 |
6 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
121 |
|
|
49 |
|
|
1 |
|
|
|
174 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
144 |
144 |
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
174 |
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Замечание. Решение данного примера векторным методом не является рациональным, но приведено с целью показа широких возможностей векторного метода при решении задач разных видов.
Тренировочные упражнения
7. В единичном кубе ABCDA1B1C1D1 найдите расстояние от точки A до пря-
мой: a) B1D1; б) А1С ; в) BD1 .
8. В правильной треугольной призме ABCA1B1C1 , все ребра которой равны 1, найдите расстояние от точки A до прямой ВС1.
9. В правильной треугольной призме ABCA1B1C1 высота равна 1, сторона основания равна 2. Найдите расстояние от точки A1 до прямой BС1.
10. (МИОО). В правильной треугольной призме ABCA1B1C1 высота равна 2, сторона основания равна 1. Найдите расстояние от точки В1 до прямой AС1 .
11. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все ребра которой равны 1, найдите расстояние от точки A до прямой: а) DЕ; б) D1E1 ;
в) B1C1; г) BE1 ; д) BC1; е) CE1 ; ж) CF1 ; з) CB1.
12.В правильной шестиугольной
призме ABCDEFA1B1C1D1E1F1 , стороны основания которой равны 5, а боковые ребра равны 11, найдите расстояние от точки C до прямой A1F1 .
13. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания равна 3, а боковое ребро равно 2. Найдите расстояние от точки E до прямой B1C1 .
14. (ЕГЭ, 2011). В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , стороны оснований которой равны 4, а боковые ребра равны 3, найдите расстояние от точки C до прямой D1E1.
15. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все ребра которой равны 1, найдите расстояние от точки A до прямой CB1.
16. Основание прямой призмы ABCDA1B1C1D1 ромб ABCD, в котором
АВ 10, |
АС 6 7. Боковое ребро АА1 |
04.12.2012 |
9 |
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
равно 3
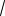 21. Найдите расстояние от вершины В до прямой АС1.
21. Найдите расстояние от вершины В до прямой АС1.
17.В тетраэдре ABCD, все ребра которой равны 1, найдите расстояние от точки A до прямой, проходящей чрез точку B и середину ребра CD.
18.В правильной четырехугольной пирамиде SABCD с основанием ABCD сторона основания равна 2, а боковое ребро равно 4. Точка M – середина SD. Найдите расстояние от точки A до прямой MB.
19.(МИОО). В правильной четырехугольной пирамиде SABCD сторона осно-
вания равна 1, а боковое ребро равно
3 . Найдите расстояние от точки C до
2
прямой SA.
20.В правильной шестиугольной пирамиде SABCDEF, стороны оснований которой равны 1, а боковые ребра равны 2, найдите расстояние от точки C до прямой SF.
21.В правильной шестиугольной пирамиде SABCDEF , стороны оснований которой равны 1, а боковые ребра равны 2, найдите расстояние от точки C до прямой SA.
22.В правильной шестиугольной пирамиде MABCDEF, стороны основания
которой равны 1, а боковые ребра равны 2, найти расстояние от точки F до прямой BT , где T – середина ребра MC .
04.12.2012 |
10 |
3.Расстояние от точки до плоскости
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллель-
ной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
Расстояние между двумя параллель-
ными плоскостями равно длине их общего перпендикуляра.
Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
Поэтапно-вычислительный метод
При решении задачи этим методом строится перпендикуляр из заданной точки на плоскость и вычисляется его длина.
Пример 11. Найти расстояние от точки S до плоскости треугольника ABC, если из-
вестно, что SA 2, |
AB AC 4 и |
||
SB SC BC 2 |
3 |
. |
|
Решение. Пусть M – середина BС (см. рис. 10). Тогда SM и AM – медианы (и вы-
соты) равно- |
|
||
бедренных |
тре- |
|
|
угольников |
|
|
|
ABC и SBC. Так |
|
||
как SM BC и |
|
||
AM BC , |
то |
|
|
BC ASM |
(по |
Рис. 10 |
|
признаку |
пер- |
||
|
|||
пендикулярности прямой и плоскости). |
|||
Плоскость ASM ABC по признаку перпендикулярности плоскостей (плоскость ABC содержит прямую BC). Следовательно, перпендикуляр SH , проведенный из точки S на прямую пересече-
ния этих плоскостей |
AM и есть перпен- |
|
дикуляр к плоскости ABC. Значит иско- |
||
мое расстояние равно высоте SH |
в тре- |
|
угольнике ASM , |
в котором |
SA 2, |
SM 3 и AM 
 13. Обозначим AH x,
13. Обозначим AH x,
www.alexlarin.net
