
C22013
.pdf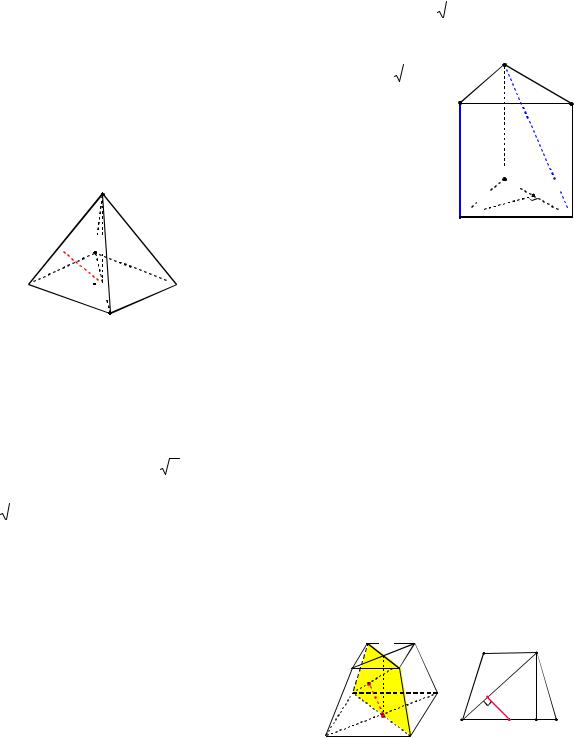
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
ка A проекция AA1 на эту плоскость. Проекцией D1C на плоскость ABC является DC. Расстояние от точки A до DC. равно a.
Ответ: a.
Поэтапно-вычислительный метод
Пример 25. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найти расстояние между прямыми BD и SA.
Решение. Пусть E – основание перпендикуляра (см. рис. 27), опущенного из точки O на ребро SA. Так как BD AOS (объясните), то BD OE .
S
E
 B
B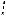

A

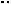





 O
O









 C
C
D
Рис. 27
Таким образом, OE – общий перпендикуляр к скрещивающимся прямым BD и SA. Найдем его длину как высоту OE , опущенную на гипотенузу AS треуголь-
ника |
AOS . Так как AO |
2 |
, AS 1, |
||||
2 |
|||||||
|
|
|
|
|
|
||
|
|
|
|
, то OE 0,5. |
|
|
|
SO |
|
2 |
|
|
|||
2 |
|
Ответ: 0,5. |
|||||
|
|
|
|||||
|
|
|
|
|
|||
Метод параллельных прямой и плоскости
В общем случае не обязательно строить общий перпендикуляр.
Пример 26. В правильной треугольной призме ABCA1B1C1 , все рёбра которой равны 1, найти расстояние между прямыми АA1 и B1C .
Решение. Прямая B1C лежит в плос-
кости |
BCC1 |
(см. рис. 28). Так как |
AA1 ||CC1 , то |
АA1 || BCC1. Для нахожде- |
|
ния |
искомого |
расстояния достаточно |
04.12.2012 |
21 |
|
найти |
расстояние от точки А |
прямой |
|||||||||
АA1 |
до плоскости BCC1 . Плоскости |
||||||||||
ABC и BCC1 |
перпендикулярны и пере- |
||||||||||
секаются по прямой BC. В равносторон- |
|||||||||||
нем |
треугольнике |
ABC |
высота |
||||||||
AD BC , поэтому |
AD BCC1 . Отсюда |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
следует, что |
AD |
3 |
|
|
– искомое рас- |
||||||
2 |
|
|
|||||||||
стояние. |
|
|
|
|
|
|
B1 |
|
|||
|
|
|
|
|
|
|
|
|
|||
Ответ: |
|
3 |
|
. |
|
|
|
|
|
|
|
2 |
|
A1 |
|
C1 |
|||||||
|
|
|
|
|
|||||||
Замечание.
Отметим, что в свою очередь последнюю задачу
можно свести к 
 задаче о нахож- A
задаче о нахож- A


 дении расстояния от произвольной
дении расстояния от произвольной
точки прямой до плоскости.
 B
B

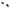 D
D 
 C
C
Рис. 28
Метод ортогонального проектирования
Пример 27. В правильной усечённой четырехугольной пирамиде ABCDA1B1C1D1 со сторонами оснований равными a и b (a b), и высотой h найти расстояние между диагональю BD1 и диагональю большего основания AC .
Решение. Прямые BD1 и AC скрещиваются (см. рис. 29а). Точки O и O1 точки пересечения диагоналей оснований пирамиды. OO1 AC и OO1 BD , как отрезок, соединяющий середины оснований равнобедренных трапеций BB1D1D и AA1C1C.
B1 O1 |
C1 |
B1 |
D1 |
A1 |
D1 |
|
|
K |
C |
K |
|
B |
|
||
|
|
|
|
O |
|
B |
O N D |
AD
аб
Рис. 29
Построим плоскость перпендикулярную одной из скрещивающихся прямых
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
BD1 и AC . |
Плоскость BB1D1 AC , так |
|
как AC перпендикулярна двум пересе- |
||
кающимся |
прямым этой |
плоскости: |
AC BD ( ABCD квадрат) |
и AC OO1 |
|
(OO1 высота пирамиды). |
Прямая BD1 |
|
лежит в плоскости BB1D1 , поэтому искомое расстояние равно длине перпендикуляра, опущенного из точки O на BD1. OK найдем из подобия прямоугольных треугольников BD1N и BKO (см. рис. 29б), имеющих общий острый угол. В треугольнике BD1N :
D1N h, BN BD ND
a |
|
|
|
(a b) |
2 |
|
|
(a b) 2 |
, |
|
|
||||
2 |
|||||||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|||||
BD |
|
|
|
|
|
h2 |
(a b)2 |
. |
|||||||
D N2 |
BN2 |
||||||||||||||
|
|||||||||||||||
1 |
1 |
|
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||
В треугольнике BKO BO BD a 2 .
2 .
2 2
Тогда OK BO или
D1N BD1 |
|
|
|
|
|
|
|
|
|
||
OK |
|
BO D1N |
|
|
|
ah |
|
. |
|
|
|
BD1 |
|
|
|
|
|
|
|
|
|||
|
|
2h2 (a b)2 |
|||||||||
|
|
|
|
|
|
|
|
||||
|
|
Ответ: |
|
ah |
|
|
|
. |
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||
2h2 (a b)2
Продемонстрируем применение всех указанных методов на следующем примере.
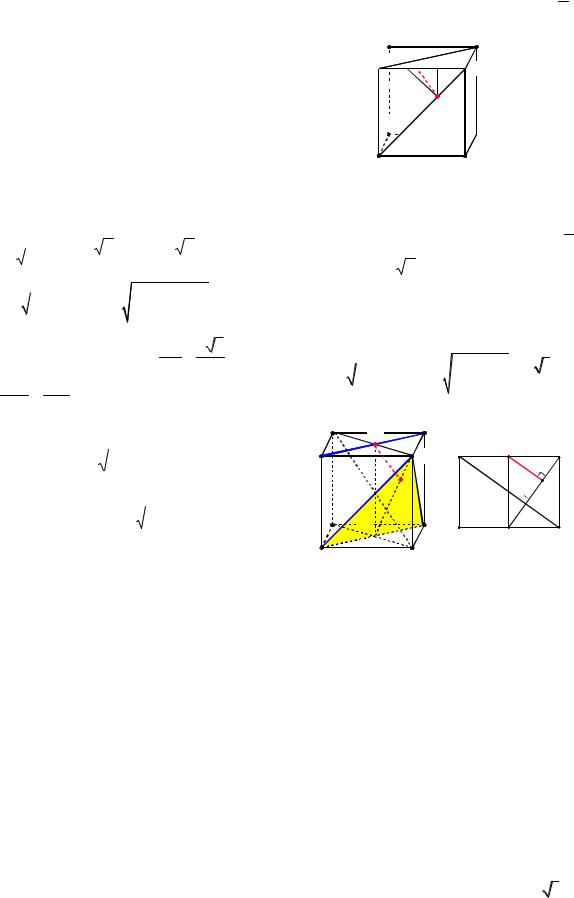
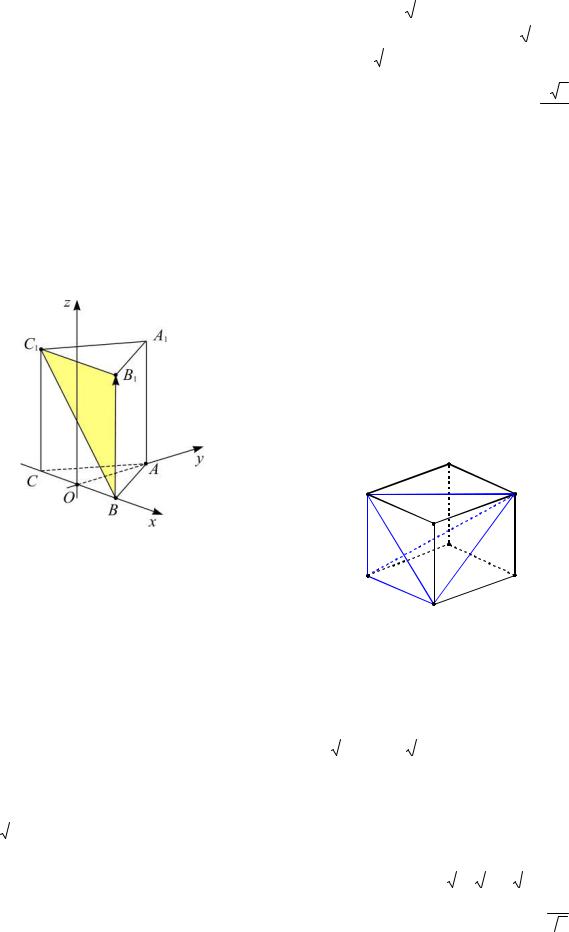
Пример 28. Найти расстояние между непересекающимися диагоналями двух смежных граней куба, длина ребра которого равна a.
Решение. Найдем расстояние между диагоналями A1C1 и AD1 куба
ABCDA1B1C1D1 .
1-й способ. Пусть отрезок PQ (см. рис. 30) есть общий перпендикуляр скрещи-
вающихся прямых A1C1 |
и AD1 , а PN и |
||||
KQ его |
ортогональные |
проекции на |
|||
плоскости A1B1C1 и AA1D1 соответственно |
|||||
(PK A1D1 |
и |
QN A1D1). |
На основании |
||
теоремы |
|
о |
трех |
перпендикулярах |
|
PN AC |
и |
KQ AD . |
Треугольники |
||
1 |
1 |
|
1 |
|
|
04.12.2012 |
|
|
|
|
22 |
A1PN и KQD1 прямоугольные и равно-
бедренные, поэтому A1K KN ND1 a . 3
B1 C1
A1
 P
P

 N
N  D1
D1
 K
K
Q
 B
B












 C
C
A D
Рис. 30
Аналогично, NQ ND1 A1K KP a
3
и AP PN |
a 2 |
. Тогда из прямоуголь- |
||||||||||||||
|
||||||||||||||||
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ного треугольника PNQ получим рас- |
||||||||||||||||
стояние между A1C1 и AD1 : |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2a2 |
|
a2 |
|
|
a |
|
|
. |
||
|
|
|
|
|
|
|
3 |
|||||||||
PQ |
PN2 NQ2 |
|||||||||||||||
9 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
9 |
|
|
|
3 |
|
|
|
|||
B1 |
O |
C1 |
B1 |
|
O |
|
D1 |
|||||||||
A1 |
|
|
D1 |
|
|
|||||||||||
|
|
N |
|
|
|
|
|
|
|
h |
N |
|||||
B O1 |
|
C |
B |
|
O1 |
|
D |
|||||||||
|
|
|
|
|
|
|
|
|||||||||
AD
аб
Рис. 31
2-й способ. Построим плоскость, содержащую AD1 и параллельную A1C1 (см. рис. 31а). Искомой плоскостью является AD1C . Найдем расстояние до нее от ка- кой-либо точки прямой A1C1. Для этого опустим из точки O (см. рис. 31а) на указанную плоскость перпендикуляр. Плос-
кости |
BB1D1 и AD1C перпендикулярны |
|||||||||
( AC BD и AC D1D , и AC AD1C ). |
||||||||||
|
Так как |
B1D D1O1 (см. рис. 31б) (до- |
||||||||
кажите самостоятельно!), то ON AD1C |
||||||||||
(ON || B1D) |
и из подобия треугольников |
|||||||||
BB1D и OD1N следует |
|
|
|
|
||||||
|
ON |
|
OD1 |
|
или h ON |
BD OD1 |
|
a |
3 |
. |
|
|
|
|
|
|
|||||
|
BD |
B1D |
|
B1D |
3 |
|
|
|||
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Замечание. Для нахождения расстояния от точки О до плоскости AD1C можно воспользоваться результатом примера14.
B1 |
O |
C1 |
B1 |
O |
D1 |
A1 |
K |
D1 |
|||
|
|
K |
h |
|
|
|
N |
|
N |
||
B |
C |
|
|
||
O1 |
B |
O1 |
D |
||
|
|
|
AD
аб
Рис. 32
3-й способ. Построим параллельные плоскости AD1C и BA1C1 (см. рис. 32а), содержащие прямые AD1 и A1C1 соответственно. Диагональ B1D куба перпендикулярна обеим плоскостям и (см. рис. 32б) точками K и N делится на три равные части (опорная задача № 20 глава 3 п. 3.4). Расстояние между плоскостями
AD1C и BA1C1 |
равно длине отрезка |
KN , |
||||||
т.е. |
a |
|
|
. |
|
|
|
|
3 |
|
|
|
|
||||
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
B1 |
|
|
O |
C1 |
B1 |
O |
D1 |
A1 |
|
|
|
D1 |
||||
|
|
|
|
|
N |
|
h |
N |

 B
B
 O1
O1




 C
C 






 B O1 D
B O1 D
AD
аб
Рис. 33
4-й способ. Плоскость BB1D1 перпен-
дикулярна |
прямой |
A1C1 ( A1C1 B1D1 и |
|
A1C1 D1D ) |
и |
плоскости |
AD1C |
(B1D AD1C ) (см. рис. 33а). D1O1 |
про- |
||
екция AD1 |
на плоскость BB1D1 . Расстоя- |
||
ние от точки O (проекции A1C1 на плос- |
|||
кость BB1D1 ) до D1O1 |
равно длине отрезка |
||
ON (см. рис. 33б). |
|
|
|
04.12.2012
Векторно-координатный метод
Так как задачу данного типа можно свести к задаче о вычислении расстояния от точки до плоскости, то здесь уместно применить формулу расстояния от точки до плоскости, применяя координатный метод.
Рассмотрим векторный подход к решению задач данного типа. Пусть даны прямые l1 с направляющим вектором q1
и l2 с направляющим вектором q2 . Точки
A1 и A2 лежат на прямых l1 и l2 соответ- |
|||
ственно, A1A2 |
|
|
|
m (см. рис. 34). |
|
||
q1 |
P1 |
A1 |
l1 |
|
m |
|
|
A2 |
P2 |
q2 |
|
|
l2 |
|
|
|
|
|
|
|
Рис. 34 |
|
|
Чтобы определить |
расстояние |
между |
|
прямыми l1 и l2 , то есть найти длину их
общего перпендикуляра P1P2 |
(P1 l1 |
и |
|
P2 l2 ), представим вектор P1P2 |
в виде |
|
|
|
|
|
|
P1P2 P1A1 A1 A2 A2P2 x q1 m y q |
2 . |
||
Неизвестные коэффициенты |
x, y |
на- |
|
ходятся из условия перпендикулярности
вектора P1P2 векторам q1 |
и q2 : |
|
|
|
|||||||
PP |
|
|
|
|
|
|
|
|
|
||
q 0, |
(x q |
m y q |
2 |
) q 0, |
|||||||
|
1 |
2 |
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
0. |
|||
PP q |
(x q1 |
m y q |
2 ) q2 |
||||||||
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
Искомое расстояние выражается следующим образом:
PP |
|
|
|
|
|
|
)2 . |
|
|
|
|||||||
|
(x q |
m y q |
2 |
|||||
1 |
2 |
|
|
1 |
|
|
|
|
В большинстве случаев при решении подобных задач удобнее ввести декартову систему координат, выразить векторы q1, q2 , m через ее базисные векторы и провести все вычисления в координатной форме.
Используя приведенные выводы, решим следующие задачи.
23
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
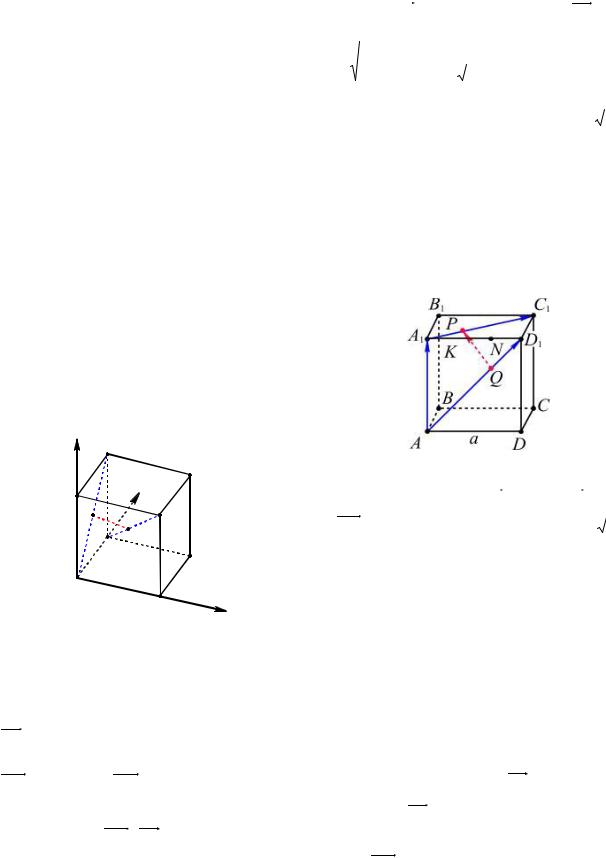
Пример 29. В единичном кубе ABCDA1B1C1D1 найти расстояние меж-
ду диагональю куба BD1 и диагональю грани AB1 .
Решение. Введем прямоугольную систему координат (см. рис. 35), тогда
А(0;0;0), В(0;1;0), В1(0;1;1), |
D1(1;0;1). |
||||||
Пусть EF – общий перпендикуляр |
|||||||
скрещивающихся прямых BD1 |
и AB1 , то |
||||||
есть EF AB1, |
EF BD1 , |
причем |
|||||
E AB |
и F BD . Обозначим |
AE |
, |
||||
|
|||||||
1 |
|
1 |
|
B1E |
|||
|
BF |
|
|
|
|||
|
и воспользуемся формулами для |
||||||
D1F |
|||||||
|
|
|
|
|
|
||
координат точки (опорная задача 1), которая делит данный отрезок в заданном отношении. Получим
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
E |
0, |
|
|
, |
|
|
|
, F |
|
, |
|
, |
|
. |
|
|
|
|
|
|
|
||||||||
|
|
1 1 |
|
|
|
|
|
|
|
|||||
|
|
1 1 1 |
||||||||||||
|
|
|
z |
|
B1 |
|
|
|
|
|
|
|
||
|
|
|
A1 |
|
|
|
y |
|
|
C1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
E |
D1 |
|
F |
||
|
||
|
B |
|
|
C |
A
|
|
|
D |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 35 |
|
|
|
||
Пусть |
|
p, |
|
|
q, |
тогда |
|
1 |
|
|
|||||
|
|
1 |
|
|
|||
E(0, p, p), |
F(q,1 q, q). |
Так как вектор |
|||||
EF {q, 1 q p, q p} |
должен |
быть |
|||||
перпендикулярным |
|
|
|
векторам |
|||
AB1 {0;1;1} и BD1 |
{1; 1;1}, то имеем |
||||||
систему уравнений: |
|
|
|
|
|
||
AB1 EF 0,

BD EF 0
1
или
1 q p q p 0, |
p |
1 |
, q |
1 |
. |
|
|
||||||
|
|
|||||
q 1 q p q p 0 |
2 |
3 |
|
|||
04.12.2012 |
|
|
24 |
|||
Отсюда EF |
|
1 |
, |
1 |
, |
1 |
|
, EF |
|
EF |
|
|
|||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
6 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||
9 |
36 |
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
6 |
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
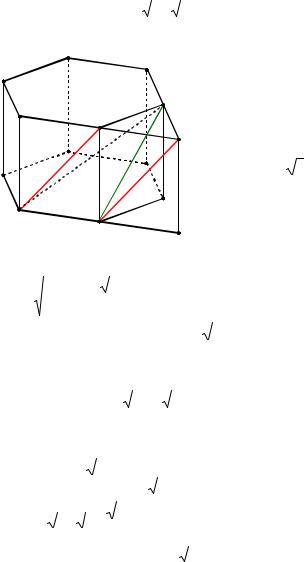
Пример 30. Найти расстояние между непересекающимися диагоналями двух смежных граней куба, длина ребра которого равна a.
Решение. Найдем расстояние между диагоналями A1C1 и AD1 куба
ABCDA1B1C1D1 (см. рис. 36).
Рис. 36
Введем векторы A1C1 q1 и AD1 q2 ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
|
|
|
2 , |
||||||||
AA1 m. |
|
|
|
|q1 |
| |q2 | a |
|||||||||||
| m| a, |
(q1, q2 ) 60 , |
(q1, m) 90 , |
||||||||||||||
(q2 , m) 45 , то |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
q |
q |
|
q 2 2a2 , |
|
|
|
|||||
|
|
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 a2 , |
|
|
|||||||
q2 |
q2 |
q22 2a2 |
, m m |
m |
|
|
||||||||||
|
q |
q |
2 |
| q |
| | q |
| cos60 a2 , |
|
|
||||||||
|
1 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
q1 m | q1 |
|
| | m| cos90 0, |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
q2 |
m | q2 |
| | m| cos45 a2 . |
|
|
|||||||||||
Пусть отрезок QP есть общий перпен- |
||||||||||||||||
дикуляр скрещивающихся прямых A1C1 |
и |
|||||||||||||||
AD1 . Представим вектор QP в виде |
|
|
||||||||||||||
|
|
|
|
QP x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
q1 m y |
q2 . |
|
|
|
||||||||
Из условия перпендикулярности век- |
||||||||||||||||
тора PP векторам q |
и q |
2 |
получаем |
|
|
|||||||||||
|
1 |
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
(x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
||
|
q m |
q |
) q 0, |
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
y |
2 |
|
1 |
|
|
|
||
|
(x |
q1 m |
q2 ) q2 0 |
|
|
|||||||||||
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x q 2 |
m |
q |
y (q |
2 |
q ) 0, |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
x (q |
q |
2 |
|
) m |
q |
2 |
|
|
|
q |
2 |
0 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
(2x y) 0, |
|
|
|
|
|
|
2x y 0, |
|
|
|
|
|||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 2y 0. |
|
|
|
|||||||||||||||||
|
|
|
|
2 |
(x 1 2y) 0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Отсюда x |
1 |
, |
|
y |
2 |
. Тогда |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
QP |
|
|
|
|
|
|
|
q |
m |
|
|
|
q |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
||||||
|
q2 |
9m2 4q2 6(q m) 12(q |
|
m) 4(q |
q |
|
|
||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||
|
2 9 8 0 12 4 |
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
Ответ: a 3 . 3
Замечание. В большинстве случаев при решении подобных задач удобнее ввести декартову систему координат, выразить векторы q1, q2 , m через ее базисные векторы и провести все вычисления в координатной форме.
Пример 31. В правильной четырехугольной пирамиде MABCD с основанием ABCD высота и сторона основания равны 4, точки E и F середины ребер AM и DC соответственно. Найти расстояние между прямыми BE и FM.
z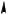
M 

y
E P
P
 Q
Q 


 B
B 



 C
C
A











 O
O



 F
F
 x
x
D
Рис. 37
Решение. Введем декартову систему координат следующим образом. Пусть начало координат O находится в центре основания, ось x проходит через точку O параллельно ребру AD, ось y проходит через точку O параллельно ребру
04.12.2012 |
25 |
AB , ось z проходит через точку O перпендикулярно плоскости основания (см. рис. 37). Тогда вершины пирамиды имеют координаты:
A( 2; 2; 0), B( 2; 2;0), C(2; 2;0),
D(2; 2; 0), M(0; 0; 4).
|
В этой системе координат E( 1; 1; 2) |
||
и |
F(2; 0; 0). |
Введем |
векторы |
BE q1 {1; 3; 2}, |
FM q2 |
{ 2; 0; 4} |
|
и |
|
|
|
EM m {1;1; 2}. |
|
|
|
Тогда
q1 q1 1 1 ( 3) ( 3) 2 2 14, q2 q2 ( 2) ( 2) 0 0 4 4 20, m m 1 1 1 1 2 2 6,
q1 q2 1 ( 2) ( 3) 0 2 4 6, q1 m 1 1 ( 3) 1 2 2 2, q2 m ( 2) 1 0 1 4 2 6.
Пусть отрезок PQ есть общий перпендикуляр скрещивающихся прямых BE и FM. Представим вектор PQ в виде
|
|
|
PQ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x q1 |
m y q2 . |
|
|||||||||||
Из условия перпендикулярности век- |
|||||||||||||||||
тора PQ векторам q1 и q2 получаем |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(x q |
m y |
q |
) q 0, |
|
||||||||||||
|
|
1 |
|
|
|
|
2 |
|
|
1 |
|||||||
|
(x q1 m y |
q2 ) q2 0 |
|
||||||||||||||
|
|
|
|
|
14x 2 6y 0, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
6x 6 20y 0. |
|
|||||||||||
Отсюда x |
|
1 |
, |
y |
18 |
|
. Тогда |
||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
61 |
|
61 |
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
18 |
|
|||||||
|
|
|
PQ |
|
q1 |
m |
|
|
q2 |
|
|||||||
|
|
|
61 |
61 |
|||||||||||||
|
1 |
{1; 3; 2} {1;1; 2} |
18 |
{ 2; 0; 4} |
|||||||||||||
|
|
||||||||||||||||
|
61 |
|
|
|
|
|
|
|
|
|
|
61 |
|
||||
1 {96; 64; 48}. 61
PQ 1 
 962 642 482 16
962 642 482 16
 61. 61 61
61. 61 61
Ответ: 16
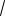 61 . 61
61 . 61
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Если скрещивающиеся прямые поместить в параллельные плоскости, то расстояние между этими прямыми будет равно расстоянию между построенными плоскостями, а оно равно расстоянию от любой точки одной прямой до плоскости, содержащей вторую прямую.
В случае применения координатного метода можно воспользоваться формулой расстояния от точки до плоскости.
Пример 32. (ЕГЭ, 2011). В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 7, найти расстояние между прямыми AA1 и BC1 .
Решение. Введем прямоугольную системукоординат, какпоказано на рис. 38.
Рис. 38
Поскольку прямые AA1 и BB1 параллельны, то плоскость C1B1B и прямая AA1
также параллельны. Плоскость C1B1B
совпадает с плоскостью грани CC1B1B и в
введенной |
системе |
координат |
задается |
|||||
уравнением |
y 0, а ее нормальный век- |
|||||||
тор |
|
имеет |
следующие координаты: |
|||||
n {0;1;0}. |
|
|
|
|||||
Так как расстояние между прямыми |
||||||||
AA1 |
и BB1 |
равно расстоянию от любой |
||||||
точки прямой AA1 |
до плоскости C1B1B, |
|||||||
то |
|
возьмем, |
например, |
точку |
||||
|
7 |
|
|
|
|
|
|
|
3 |
|
|
|
|
||||
A 0; |
|
|
|
|
; 0 и, подставив в формулу (4), |
|||
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получим:
04.12.2012 |
26 |
AA1; BB1 A;C1B1B
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 1 |
7 3 |
|
0 0 0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
7 3 |
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
02 12 02 |
2 |
|
|
||||||
Ответ: 7 3 . 2
Метод опорных задач
При решении задач этого типа можно
воспользоваться опорной задачей № |
9 |
||
(см. главу 3 п. 3.4). |
|
|
|
Если AB и CD – скрещивающиеся реб- |
|||
ра треугольной пирамиды ABCD, d |
– |
||
расстояние между ними, |
АВ а, |
||
CD b, – угол между AB и CD, V |
– |
||
объем пирамиды ABCD, то d |
6V |
. |
|
|
|
||
absin
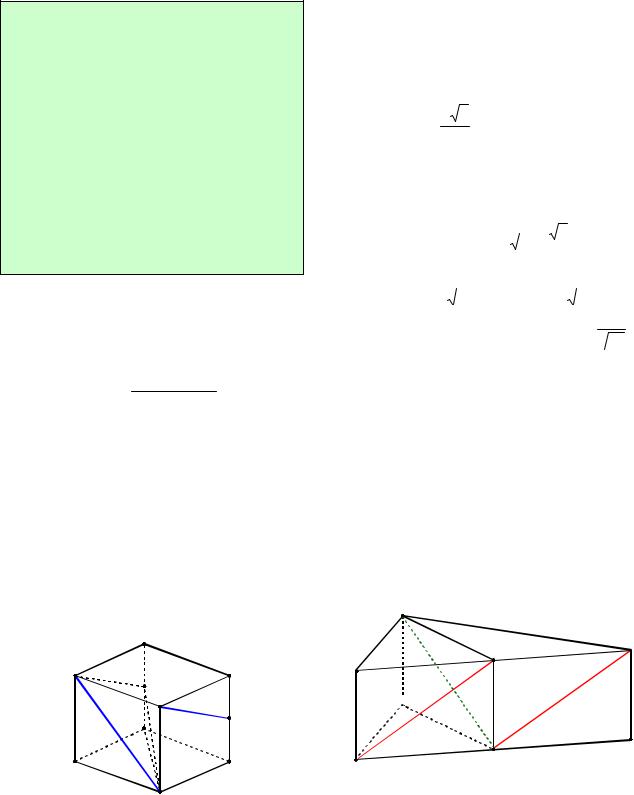
Пример 33. В единичном кубе ABCDA1B1C1D1 найти расстояние меж-
ду диагональю куба BD1 и диагональю грани AB1 .
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
D1 |
|||||
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
D |
|||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Рис. 39 |
|
|
|
|
|
|
|
|
|
|
||||
|
Решение. Найдем искомое расстояние |
|||||||||||||||||||||
по |
|
формуле d |
|
|
|
6V |
|
|
|
, |
где V – |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
AB1 BD1 sin |
|
|
|
|
|
|
|||||||||
объём |
пирамиды |
|
ABB1D1 (см. рис. 39), |
|||||||||||||||||||
AB1 |
|
|
, BD1 |
|
|
, 90 – угол меж- |
||||||||||||||||
|
2 |
3 |
||||||||||||||||||||
ду прямыми BD1 |
и AB1 . Так как площадь |
|||||||||||||||||||||
основания АВВ1 |
пирамиды ABB1D1 рав- |
|||||||||||||||||||||
на |
|
1 |
, а высота A D равна 1, то V |
1 |
. |
|||||||||||||||||
|
2 |
|
1 |
1 |
|
|
|
|
|
|
|
6 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Следовательно, d |
|
|
1 |
|
|
|
1 |
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
3 |
6 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: 1 .  6
6
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Пример 34. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найти расстояние между прямыми AB1 и BC1.
Решение. Найдем синус угла между данными прямыми. Так как AB1 ||BM , то получим косинус угла из треугольника
MBC1 (см. рис. 40):
|
BM2 BC2 |
MC2 |
|
|
|
2 2 1 |
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||||||||||||||
cos |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||
2 BM BC1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
2 4 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
||||||||||||||
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Рис. 40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Расстояние от |
||||||||||||||||||||||||||||||
Тогда sin |
1 |
9 |
|
|
|
|
7 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
точки C до |
прямой |
|
A B |
|
равно |
|
|
|
|
|
|
3 |
|
. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||
Объем пирамиды ABB1C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
с основанием |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ABB равен V |
|
|
|
1 1 |
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1 |
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB1 |
|
|
|
|
|
|
||||||||||||||||||||||||||
Расстояние |
|
между |
прямыми |
|
|
|
|
|
|
и |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
BC1 равно d |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
21 |
/7. |
|||||||||||||||||||||||||||
Тренировочные упражнения
39. В единичном кубе ABCDA1B1C1D1
найдите расстояние между прямыми АВ1
иА1C1.
40.В единичном кубе ABCDA1B1C1D1
найдите расстояние между диагональю куба BD1 и диагональю грани AB1 .
41. В правильной треугольной призме ABCA1B1C1 , все рёбра которой равны 1, найдите расстояние между прямыми AB
иА1C .
42.В правильной треугольной призме
ABCA1B1C1 сторона основания равна 1, а боковое ребро равно 3. Найдите расстояние между прямыми AB1 и BC1 .
43. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все ребра которой равны 1, найдите расстояние между прямыми AА1 и BC1.
44. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найдите расстояние между прямыми DE1 и BC1.
45. Сторона основания ABC правильной треугольной пирамиды ABCD равна
8 3 , высота пирамиды |
DO 6. Точки |
A1 , C1 – середины рёбер |
AD и CD соот- |
ветственно. Найдите расстояние между прямыми BA1 и AC1 .
46. В пирамиде DABC известны длины
рёбер: AB AC DB DC 10, |
BC |
DA 12. Найдите расстояние |
между |
прямыми DA и BC. |
|
47. В тетраэдре ABCD известно, что
AC BD 14, |
BC AD 13, |
AB |
CD 15. Найдите расстояние |
между |
|
прямыми AC и BD. |
|
|
48.В правильной четырехугольной пирамиде MABCD , все рёбра которой равны 1, найдите расстояние между прямыми MA и BC.
49.В правильной четырехугольной пирамиде SABCD с основанием ABCD сторона основания равна 3, а боковое ребро равно 4. Точка M – середина SB. Найдите расстояние между прямыми SA и MC.
50.В правильной шестиугольной пирамиде SABCDEF с основанием ABCDEF боковое ребро и сторона основания равны 5 и 3 соответственно. Точка N – середина ребра SF , а точка M делит ребро SD так, что SM :MD 1:3. Найдите расстояние между прямыми AN
иEM .
04.12.2012 |
27 |
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
1.5.Угол между двумя прямыми
Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.
0 a, b 90 .
Углом между скрещивающимися пря-
мыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.
Две прямые называются перпендикулярными, если угол между ними равен 90 .
Угол между параллельными прямыми
считается равным нулю.
Поэтапно-вычислительный метод
При нахождении этим методом угла между прямыми m и l используют формулу
cos | b2 c2 a2 | , 2bc
где a и b длины сторон треугольника АВС, соответственно параллельных этим прямым.
Пример 35. В кубе ABCDA1B1C1D1
найти угол между прямыми A1D и D1E ,
где E – середина ребра CC1.
Решение. Пусть F – середина ребра ВВ1, а – ребро куба, – искомый угол
(см. рис. 41).
|
B1 |
|
|
A1 |
F |
|
C1 |
|
|
|
|
|
B |
D1 |
E |
A |
|
|
C |
|
|
|
|
|
D |
|
|
|
Рис. 41 |
|
|
Так как |
A1F || D1E , |
то |
– угол при |
вершине A1 |
в треугольнике A1FD. Из |
||
треугольника BFD имеем |
|
||
04.12.2012 |
|
|
|
FD |
2 |
BD |
2 |
BF |
2 |
2a |
2 |
|
a2 |
9a2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||
|
|
|
|
|
4 |
4 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а из треугольника A1B1F получаем |
|
|
|
|||||||||||||||||
A F |
2 |
A B |
2 |
B F |
2 |
a |
2 |
|
|
a2 |
|
5a |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
1 |
1 |
|
1 |
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
откуда A1F a 5 . 2
Далее в треугольнике A1FD используем теорему косинусов
FD2 A1D2 A1F2 2A1D A1F cos ,
|
9a |
2 |
2a |
2 |
|
|
5a2 |
2a |
|
|
a 5 |
|
|
|
|
||||
|
|
2 |
cos , |
||||||||||||||||
4 |
|
|
4 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
откуда cos |
|
1 |
|
|
и arccos |
|
|
1 |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
10 |
|
|
10 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: arccos 1 .
 10
10
Замечание. Для упрощения вычислений длину ребра куба удобно принять за единицу.
Пример 36. В правильной треугольной
призме ABCA1B1C1 , все |
рёбра |
которой |
равны 1, найти угол между |
прямыми |
|
AС1 и B1С . |
|
|
Решение. Проведем |
CM ||AC1 (см. |
|
рис. 42). Тогда |
|
|
(AС1, B1C) (CM, B1C) .
B1
M C1 
A1
B
N
C
A
Рис. 42
Из треугольника MС1B1 с помощью теоремы косинусов находим
MB12 12 12 2 1 1 ( 0,5) 3.
Далее из треугольника MСС1 , используя теорему косинусов, получаем
28
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
cos |
2 |
2 3 |
|
|
1 |
и arccos |
1 |
. |
|||
|
|
|
|
|
|
|
|
||||
|
2 |
|
2 2 |
4 |
4 |
|
|||||
Ответ: arccos1 . 4
Пример 37. (МИОО, 2010). В пра-
вильной шестиугольной пирамиде MABCDEF , стороны основания которой равны 1, а боковые рёбра равны 2, найти косинус угла между MB и AD.
Решение. Прямая AD параллельна прямой BC (см. рис. 43). Следовательно, искомый угол MBC . В равнобедренном треугольнике MBC проведем апофему
ML, BL 1 BC 1 . 2 2
M
L

 C
C









 D
D


B



 E
E
A F
Рис. 43
Из прямоугольного треугольника
BML получаем cos MBL BL 1 .
BM 4
Ответ: 1 . 4
Векторно-координатный метод
При нахождении угла между прямыми m и l используют формулу
p q cos p q
или в координатной форме:
cos |
|
|
|
x1x2 y1 y2 |
z1z2 |
|
|
|
, (5) |
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 |
y2 |
z2 |
|
x2 |
y |
2 |
z2 |
|||
1 |
1 |
1 |
|
2 |
|
2 |
2 |
|
|
|||
где p {x1, y1, z1} и q {x2, y2, z2} век-
торы, соответственно параллельные этим прямым; в частности, для того чтобы
04.12.2012 |
29 |
прямые m и l были перпендикулярны, необходимо и достаточно, чтобы p q 0
или x1x2 y1 y2 z1z2 0.
Пример 38. В единичном кубе ABCDA1B1C1D1 найти угол между прямыми АЕ и DF, где Е и F – точки, расположенные на рёбрах CD и C1D1 так, что
DE 1 DC , C F 1C D . |
||||
3 |
1 |
3 |
1 |
1 |
Решение. Введем прямоугольную системукоординат, как указано на рисунке 44.
|
|
|
|
z |
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
A1 |
y |
|
|
|
|
F |
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
B |
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
A |
|
|
|
|
D |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда А(0;0;0), D(1;0;0), |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Е 1; |
|
|
;0 |
|
, |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
F 1; |
|
;1 |
, |
|
AE 1; |
|
|
;0 |
, DF |
0; |
|
|
|
;1 . |
|||||||||||||||||||||||||||
3 |
3 |
3 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
По формуле (5) получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
AE DF |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
cos |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
, |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
AE |
|
DF |
|
|
|
10 |
|
|
|
13 |
|
|
|
|
|
130 |
|
|
|
|
|||||||||||||||||
arccos |
|
|
2 |
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
, где искомый угол. |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
130 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: arccos |
|
|
|
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
130 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 39. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найти угол между прямыми AB1 и BF1 .
Решение. Введем прямоугольную системукоординат, как указано на рисунке 45.
|
1 |
|
3 |
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
, B |
|
|
|
|
|
||||
|
; |
|
;0 |
|
; |
;1 |
, |
||||||
Тогда А |
|
|
|
|
|
|
|||||||
|
2 |
|
2 |
|
1 |
2 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
|
1 |
|
|
3 |
|
|
|
|
|
|
F 1;0;1 , |
|
AB 1;0;1 , |
|||||||||||||||||||
B |
; |
|
;0 , |
|
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
BF |
|
3 |
|
|
3 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
; |
|
;1 . |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
По формуле (5) получаем |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
AB1 BF1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||
|
cos |
|
|
|
|
|
|
|
|
|
|
2 |
|
, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
AB1 |
|
|
BF1 |
|
|
|
|
|
|
2 2 |
8 |
|
|
||||||||||
|
|
|
|
F1 |
|
|
|
|
|
|
z |
|
|
|
|
E1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
y |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|||
|
|
A |
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
, где искомый угол. |
||||||||||||||||||||||||||
arccos |
|
|
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
8
Ответ: arccos 2 . 8
Векторный метод
При использовании данного метода применяют формулу
p q cos p q ,
где p и q векторы, соответственно параллельные данным прямым.
Пример 40. В кубе ABCDA1B1C1D1
найти угол между прямыми EF и PQ, где E, F, P, Q – середины рёбер DD1 , BC, AA1
и B1C1 соответственно.
Решение. |
Пусть |
AD a , |
AB b , |
AA1 c (см. |
рис. |
46), где |
|a | |b | |
|c | 1, a b a c b c 0.
Тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||
|
|
EF ED DC CF |
|
|
|
|
|
|
|
c b |
|
|
|
|
a, |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||
|
|
PQ PA AB BQ |
|
|
|
|
|
|
c b |
|
|
|
|
a , |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
откуда находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
PQ EF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
c b |
|
|
|
a |
|
|
|
|
|
|
c b |
|
|
a |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
1 2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
b |
|
|
|
|
c |
|
|
|
|
|
|
|
a |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
4 |
|
|
4 |
|
4 |
4 |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
2 |
|
|
|
1 |
|
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
PQ |
|
|
|
|
|
c b |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
c |
|
b |
|
|
|
|
|
|
|
a |
|
|
||||||||||||||||||||||
|
2 |
|
2 |
4 |
|
|
|
|
4 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
2 |
|
|
|
1 |
2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
EF |
|
|
|
c b |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
c |
|
b |
|
|
|
|
|
|
a |
|
|
||||||||||||||||||||||||
2 |
2 |
|
4 |
|
|
|
4 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A



 C
C
D
Рис. 46
Подставляя полученные значения в формулу, имеем:
cos |
|
|
|
PQ EF |
|
|
1 |
: |
3 |
|
1 |
. |
||||
|
|
|
PQ |
|
|
|
EF |
|
2 |
2 |
3 |
|||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда arccos1 , где искомый
3
угол.
Ответ: arccos1 . 3
04.12.2012 |
30 |
www.alexlarin.net
