
file_12171 / МОР Пособие
.pdfА.П.Попов
Методы оптимальных решений
Пособие для студентов экономических специальностей вузов
Ростов-на-Дону
2013
Введение
Вприкладной математике имеется несколько направлений, играющих важную роль в решении целого ряда экономических задачах, и настолько тесно связанных между собой, что иногда трудно понять, где заканчивается одно направление и начинается другое. Речь здесь идет об исследовании операций, теории принятия решения и методах оптимизации. Изначально исследование операций и теория принятия решений служили двумя разными обозначениями одного и того же направления исследований в прикладной математике. Со временем произошло разделение круга задач, решаемых теорией исследования операций и теорией принятия решений, но методы исследования остались общими. Наиболее важным разделом исследования операций является математическое программирование, основная задача которого заключается в поиске экстремума (минимума иди максимума) целевой функции, зависящей от одного или нескольких аргументов, на область изменения которых накладываются ограничения. В зависимости от вида целевой функции и ограничений на область изменения ее аргументов, математическое программирование подразделяется на линейное, выпуклое, квадратичное и общее нелинейное. По сложившейся традиции, содержание ряда дисциплин, которые читают студентам экономических специальностей, включает задачи, либо прямо относящиеся к линейному программированию (задача оптимального использования ресурсов, транспортная задача), либо сводящиеся каким-то образом к задачам линейного программирования (например, теория антагонистических игр с нулевой суммой). В то же время задачи нелинейного программирования в стандартных учебных курсах обычно не рассматриваются, хотя, начиная с работ Р. Беллмана и Э. Полака, под методами оптимальных решений понимают в первую очередь именно универсальные численные методы, специально разработанные для решения задач нелинейного программирования.
Впособии изучаются простейшие задачи оптимизации, сводящиеся к поиску минимума целевой функции, зависящей от одного или нескольких действительных аргументов. Целевая функция предполагается нелинейной, хотя и достаточно гладкой, но при этом на область изменения аргументов целевой функции в многомерном случае не накладывается никаких жестких ограничений, поскольку введение подобных ограничений резко усложняет решение задачи оптимизации. В первой части пособия приводится типичная постановка и методы решения задачи оптимизации в одномерном случае, а во второй части рассматривается задача оптимизации в многомерном случае.
2
1. Выбор оптимального решения в одномерном случае
Выбор оптимального решения в одномерном случае в наиболее общей постановке сводится к поиску минимума непрерывной целевой функции, заданной на некотором достаточно хорошем подмножестве множества всех действительных чисел (поиск максимума сводится к поиску минимума изменением знака целевой функции). Для решения задачи оптимизации в столь общей постановке могут быть привлечены лишь наиболее общие (и именно потому малоэффективные) методы.
Мы будем предполагать целевую функцию не только непрерывной, но и достаточно гладкой (имеющей производные достаточно высокого порядка), что позволяет привлечь для решения задачи оптимизации эффективные методы, использующие мощный аппарат дифференциального исчисления.
Ограничившись довольно скромными требованиями к гладкости целевой функции, поставим задачу оптимизации следующим образом: найти минимум трижды непрерывно дифференцируемой целевой функции ( ), заданной на конечном отрезке [ , ]. При решении задачи будем исходить из предположения, что на данном отрезке целевая функция имеет единственный минимум, который достигается во внутренней точке отрезка.
Поскольку в точке минимума дифференцируемой функции ее первая производная обращается в ноль, задача поиска минимума целевой функции:
( ) → |
(1.1) |
сводится к задаче поиска корня ее первой производной:
( ) = 0, где ( ) = ( ) |
(1.2) |
Для решения этой задачи разработаны эффективные численные методы, допускающие реализацию в виде итерационных процедур (алгоритмов), приводящих к решению задачи с заданной точностью за конечное число шагов (разумеется, число шагов зависит от конкретного вида функции и точности вычислений). Ввиду ограниченного объема пособия мы опишем здесь лишь один из этих методов, получивший название комбинированного метода секущих и касательных. Метод возник как результат соединения двух других методов поиска корней достаточно гладкой функции – метода секущих и метода касательных, причем комбинированный метод оказался намного более эффективным, чем оба эти метода, взятые по отдельности.
3

Относительно производной целевой функции |
( ) |
будем предполагать |
||||||||||||||
выполненными следующие три условия: |
|
|
|
|
|
|
|
|||||||||
A) Функция |
|
|
на отрезке |
|
является монотонно неубывающей |
|||||||||||
(монотонно |
невозрастающей) функцией; |
|
|
|
|
|
|
|
|
|
||||||
|
|
( |
) |
|
[ , ] |
|
|
|
|
|
|
|
|
|
||
B) Функция |
( |
) |
на концах отрезка |
[ , |
|
] |
принимает противоположные |
|||||||||
по знаку значения. |
|
|
|
|
|
[ |
, ] |
|
||||||||
C) Вторая производная функции |
|
на отрезке |
является строго |
|||||||||||||
|
|
|
|
|
|
|
функцией. |
|
|
|||||||
положительной (строго отрицательной) ( |
) |
|
|
|
|
|
|
|||||||||
При выполнении условий A и B функция |
|
|
обязательно имеет внутри |
|||||||||||||
отрезка |
[ , |
] |
корень, причем единственный, |
что позволяет обойти проблему |
||||||||||||
|
|
|
|
( ) |
|
|
|
|
||||||||
отделения и уединения корней уравнения (методы решения этой непростой проблемы подробно обсуждаются в специальной литературе). Условию C имеет наглядный геометрический смысл: если оно выполняется, то функция ( ) на отрезке [ , ] является строго вогнутой (строго выпуклой) функцией. Вкратце опишем теперь метод секущих и метод касательных, которые
лежат в основе комбинированного метода.
В методе секущих корень уравнения (1.2) заменяется корнем уравнения
секущей (прямой линии, проходящей через концевые точки графика |
( )): |
|||
( − ) ( ) + ( − |
) ( ) |
= 0, |
(1.3) |
|
|
− |
|
||
Корень линейного уравнения (1.3) легко находится, и равен: |
|
|||
= |
( ) − ( ) |
(1.4) |
||
( ) − |
( ) |
|
||
В методе касательных корень уравнения (1.2) заменяется корнем уравнения касательной к графику функции ( ), проведенной через одну из концевых точек графика:
( ) + |
( )( |
− |
) = 0 |
(1.5a) |
( ) + |
( )( |
− |
) = 0 |
(1.5b) |
Возникает вопрос: какую именно концевую точку отрезка [ , ] следует при этом выбрать?
4

Можно показать, что при выполнении условий A, B и C обязательно выполняется одно из двух взаимоисключающих неравенств:
( ) |
( ) > 0 |
(1.6a) |
( ) |
( ) > 0 |
(1.6b) |
Если выполняется условие (1.6a), то выбирают уравнение касательной (1.5a), корень которого равен:
= − |
( ) |
(1.7a) |
( ) |
а если выполняется условие (1.6b), то выбирают уравнение касательной (1.5b), корень которого равен:
= − |
( ) |
(1.7b) |
( ) |
Можно показать, что при выполнении условий A, B и C точное значение корня уравнения (1.2) заключено между приближенными значениями корня
и |
, найденными методом секущих и методом касательных. Именно этот |
|
фактcлежит в основе комбинированного метода, где приближенные значения |
||
корня |
и становятся новыми границами интервала, в котором заключено |
|
точное |
значение корня уравнения (1.2). |
|
c |
||
Итерационный процесс, основанный на комбинированном методе, позволяет получить последовательность вложенных интервалов, содержащих корень уравнения (1.2), причем длины вложенных интервалов достаточно быстро стремится к нулю.
Алгоритм 1.1. Итерационный процесс на основе комбинированного
метода секущих и касательных. |
|
|
|
|
|
|
|
||
Шаг 0. Ввести исходные данные |
|
. |
Параметр задает точность |
||||||
вычисления корня, по достижении которой, |
выполнение, |
основного алгоритма |
|||||||
прерывается. Присвоить стартовое значение счетчику числа итераций |
. |
||||||||
Шаг 1. |
Увеличить значение счетчика |
|
, и найти |
приближенные |
|||||
|
|
|
← 0 |
||||||
значения |
и |
корня методом секущих |
(1.4) и касательных (1.7). |
|
|||||
|
|
← |
+ 1 |
|
|
|
|||
Шаг 2. Если | − | < |
, то перейти к шагу 4. |
|
|
5 |
|||||
|
|
|
|
|
|
|
|
|
|
Шаг 3. Выполнить следующие действия: |
и перейти к шагу 1; |
|
|||||||
1) Если |
|
< |
, то присвоить |
← |
, |
← |
|
||
2) Если |
, то присвоить |
, |
и перейти к шагу 1. |
|
|||||
Шаг 4. |
Выход из основного алгоритма, и оформление сводной таблицы |
||||||||
|
< |
|
|
← |
|
← |
|
|
|
с результатами вычислений. |
|
|
|
|
|
|
|||
Найдем в качестве примера минимум целевой функции: |
(1.8) |
||||||||
|
|
|
( ) = 0.03 |
+ 0.02 |
+ 0.18 |
− 0.5 + 0.5 |
|||
на отрезке |
|
, для чего применим описанный выше алгоритм 1.1 к |
|||||||
|
|
производной: |
|
|
|
|
|
|
|
поиску корня ее [0,2] |
|
+ 0.06 |
+ 0.36 − 0.5 |
(1.9) |
|||||
|
|
|
( ) = 0.12 |
||||||
при следующих значениях входных данных: |
|
(1.10) |
|||||||
1.5 |
|
|
= 0 |
|
= 2 |
|
= 0.00001 |
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
0 |
|
|
0.5 |
|
1 |
|
1.5 |
2 |
|
0.5 |
|
|
|
|
|
|
|
|
|
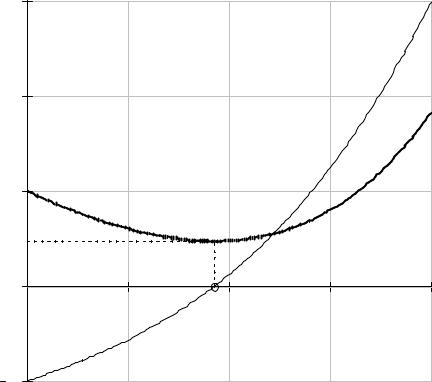
Рис.1.1. Графики целевой функции (1.8) и ее производной (1.9). |
|
||||||||
6
Пользуясь формулами для первой и второй производных полинома (1.9):
( ) = 0.36 |
+ 0.12 + 0.36 |
(1.11) |
( ) = |
0.72# + 0.12 |
(1.12) |
нетрудно убедиться, что на отрезке [0,2] условия A, B и C для функции ( ) выполнены.
1.5 |
|
|
|
|
1 |
|
|
|
|
0.5 |
|
|
|
|
0 |
0.5 |
1 |
1.5 |
2 |
0.5 |
|
|
|
|
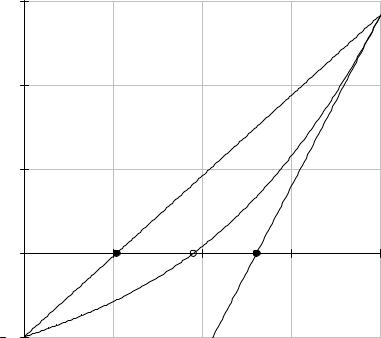
Рис.1.2. Производная (1.9) целевой функции (1.8) вместе с секущей и касательной к графику производной.
приближенные значения корня |
|
и |
|
|
=, |
0.9512072 |
и |
||
На рис. 1.2 |
показано также точное значение корня |
|
|
||||||
первой итерации |
методом |
|
= 0.52083 |
|
|
= 1.30392 |
найденные в |
||
|
|
|
|
|
|
|
|
||
|
|
секущих и методом |
|
касательных. Результаты |
|||||
применения комбинированного метода к поиску минимума целевой функции (1.8) приведены ниже в таблице 1.1, где указаны значения целевой функции, а также ее первой производной, вычисленные на концах цепочки вложенных интервалов. Как видно из этой таблицы, заданная нами довольно высокая точность вычислений достигается всего лишь за 4 итерации, что служит эмпирическим подтверждением быстрой сходимости итерационного процесса, основанного на комбинированном методе секущих и касательных.
7

Таблица 1.1. Поиск минимума комбинированным методом.
|
|
1 |
2 |
3 |
4 |
|
|
0.5208333 |
0.8754355 |
0.9491522 |
0.9512057 |
|
|
1.3039216 |
1.004902 |
0.9526257 |
0.9512082 |
( |
) |
-0.2792697 |
-0.0583492 |
-0.001642 |
-0.0000012 |
( |
) |
0.3374575 |
0.0441278 |
0.0011355 |
0.0000008 |
( |
) |
0.2934447 |
0.2312709 |
0.2290338 |
0.2290321 |
( |
) |
0.2851377 |
0.2302062 |
0.2290329 |
0.2290321 |
Теоретические оценки скорости сходимости итерационных процессов, использующихся при поиске корней достаточно гладких функций, приводятся в специальной литературе. Там же можно найти описание других методов поиска корней и экстремумов непрерывных (но не обязательно гладких) функций, например, метода дихотомии, метода золотого сечения, метода Фибоначчи и т.д.
8
2. Выбор оптимального решения в многомерном случае
Во введении уже говорилось, что наиболее простым классом задач оптимизации являются задачи поиска экстремума непрерывной функции одной или нескольких действительных переменных. При этом, как правило, речь идет о поиске локального минимума, в некотором смысле ближайшего к стартовой точке, с которой начинается итерационный процесс, за конечное число шагов приводящий к искомому решению с заданной точностью. Здесь дается описание общей алгоритмической схемы подобного итерационного процесса, и вводятся единые обозначения, пригодные для работы в пространствах любой конечной размерности. Итак, пусть целевая функция
зависит от |
аргументов |
|
|
|
. Любую совокупность значений этих |
||||
аргументов можно считать |
координатами точки |
|
в |
– мерном |
|||||
, |
, , … |
|
задана на всем |
– мерном |
|||||
пространстве. Будем считать, что целевая функция ( , |
, , … ) |
|
|
||||||
пространстве, и обозначать через |
|
|
значение функции в точке |
. Кроме |
|||||
того, будем предполагать, |
что |
целевая функция не только непрерывна, но |
|||||||
|
( ) |
|
|
|
|
||||
имеет также непрерывные частные производные первого и второго порядка. Приведем теперь описание самой алгоритмической схемы. Алгоритмическая схема 2.0. Схема поиска минимума функции многих
переменных. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Шаг 0. Задать точность |
|
вычисления |
|
минимума |
целевой функции. |
||||||||||
Выбрать стартовую точку и присвоить счетчику итераций значение |
. |
||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
точке |
Шаг 1. Вычислить текущее значение целевой функции |
|
|
в |
← 0 |
|||||||||||
( , , , … ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Шаг 2. Определить направление поиска |
|
|
|
|
|
, |
и выбрать |
||||||||
величину перемещения (шага) |
|
в данном |
направлении. |
Найти следующую |
|||||||||||
|
|
|
( |
, |
, |
|
, … ) |
|
|
. |
|||||
точку в итерационной |
последовательности по формуле: |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
в новой точке. |
|||||
Шаг 3. Вычислить значение целевой функции |
( |
>) |
> = |
|
+ |
|
|||||||||
Шаг 4. Если |
|
( |
)| < |
, перейти к |
|
|
|
|
|
||||||
|
|
|
|
|
шагу 5, иначе присвоить |
||||||||||
счетчику итераций| ( >) − |
|
|
|
, и перейти к шагу 1. |
|
||||||||||
следующее значение |
|
|
|
|
|||||||||||
Шаг 5. Выход из основного |
алгоритма и оформление сводной таблицы с |
||||||||||||||
|
← |
|
+ 1 |
|
|
|
|
|
|
|
|
||||
результатами вычислений.
Чтобы превратить алгоритмическую схему 2.0 в полноценный алгоритм, следует указать конкретные процедуру определения направления поиска и выбора величины шага в данном направлении, причем различные методы поиска минимума отличаются в первую очередь процедурой выбора направления поиска при очередной итерации. Далее мы рассмотрим всего лишь два простейших градиентных метода – метод наискорейшего спуска и метод сопряженных градиентов (градиентными называются методы поиска минимума, реализации которых требует не только наличия производных у целевой функции, но и эффективных методов их вычисления).
9

Вместе с тем в подавляющем большинстве известных алгоритмов при выборе шага руководствуются универсальным правилом: при заданном
направлении поиска величину шага |
|
следует выбрать так, чтобы минимум |
||||||||
при |
|
( ) = ( |
+ |
) |
|
зависящей от одной переменной |
, достигался |
|||
функции |
|
= |
|
|
, |
|
|
|
|
|
|
значении |
: |
|
|
min( ;F) |
( ) = ( ) |
(2.1) |
|||
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||
Если функция ( ) имеет единственный минимум, то для его поиска можно использовать известные численные методы, в частности, описанный в предыдущем разделе комбинированный метод секущих и касательных.
Напомним теперь определение градиента функции многих переменных, которое далее потребуется нам при описании метода наискорейшего спуска и метода сопряженных градиентов.
Градиентом ( ) целевой функции ( ) в точке называют вектор, проекции которого на координатные оси совпадают с частными производными первого порядка от целевой функции, взятыми в данной точке по соответствующим аргументам:
= H( ) = |
K |
K |
|
K |
|
|
|
K |
, |
K |
, |
K |
, … |
(2.2) |
|
Перейдем теперь к непосредственному описанию метода наискорейшего спуска и метода сопряженных градиентов.
Метод наискорейшего спуска является простейшим из градиентных методов поиска минимума целевой функции, где в качестве направления поиска при каждой итерации выбирается направление, противоположное градиенту целевой функции в данной точке (его называют направлением наискорейшего спуска):
|
|
|
= − = − H( |
) |
|
|
|
|
|
|
|
(2.3) |
|
Алгоритм 2.1. Поиск минимума функции многих переменных методом |
|||||||||||||
наискорейшего спуска. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Шаг 0. Задать точность вычисления |
минимума целевой |
функции. |
|||||||||||
Выбрать стартовую точку |
|
|
|
|
|
|
|
в |
|
← 0. |
|||
и присвоить счетчику итераций значение |
|
. |
|||||||||||
Шаг 1. Вычислить текущее значение целевой функции |
|
|
|
точке |
|
||||||||
Шаг 2. Определить направление поиска |
|
в |
соответствии с (2.3), |
и |
|||||||||
|
|
|
( |
) |
|
|
|
|
|||||
выбрать величину шага |
|
согласно правилу (2.1). Найти следующую точку в |
|||||||||||
итерационной |
последовательности по формуле: |
> = |
+в |
. |
|
|
|
|
|||||
|
|
|
|
|
( |
>) |
|
|
|
|
|
||
Шаг 3. Вычислить значение целевой функции |
|
новой точке. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
