
Бычков 3 курс 2 семестр все лабы / ЗАДАНИЕ / ЛР6_Maple
.pdf
Лабораторная работа
Решение задач теории вероятностей в Maple
Задание 1. Однородные цепи Маркова
Пусть { 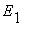 ,
, 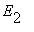 , ...,
, ...,  ,...} - множество возможных состояний некоторой физической системы. В любой момент времени система может находитьcя только в одном состоянии. С течением времени система переходит последовательно из одного состояния в другое. Каждый такой переход называется шагом процесса.
,...} - множество возможных состояний некоторой физической системы. В любой момент времени система может находитьcя только в одном состоянии. С течением времени система переходит последовательно из одного состояния в другое. Каждый такой переход называется шагом процесса.
Для описания эволюции этой системы введем последовательность дискретных случайных величин
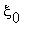 ,
, 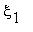 ,...,
,..., 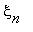 ,... Индекс n играет роль времени. Если в момент времени n система находилась
,... Индекс n играет роль времени. Если в момент времени n система находилась
в состоянии 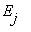 , то мы будем считать, что
, то мы будем считать, что 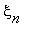 =j. Таким образом, случайные величины являются номерами состояний системы.
=j. Таким образом, случайные величины являются номерами состояний системы.
Последовательность 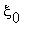 ,
, 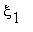 ,...,
,..., 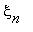 ,... образует цепь Маркова, если для любого n и любых
,... образует цепь Маркова, если для любого n и любых
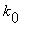 ,
, 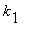 , ...,
, ..., 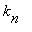
P( 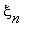 =j|
=j| 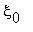 =
= 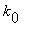 , ...,
, ..., 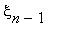 =i)=P(
=i)=P( 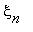 =j|
=j|  =i).
=i).
Для цепей Маркова вероятность в момент времени n попасть в состояние 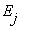 , если известна вся предыдущая история изучаемого процесса, зависит только от того, в каком состоянии находился процесс в момент n-1; короче: при фиксированном "настоящем" "будущее" не зависит от "прошлого". Свойство независимости "будущего" от "прошлого" при фиксированном "настоящем" называется марковским свойством.
, если известна вся предыдущая история изучаемого процесса, зависит только от того, в каком состоянии находился процесс в момент n-1; короче: при фиксированном "настоящем" "будущее" не зависит от "прошлого". Свойство независимости "будущего" от "прошлого" при фиксированном "настоящем" называется марковским свойством.
Вероятности 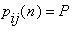 (
( 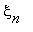 =j|
=j|  =i), i, j=1,2,..., r называются матрицами перехода из состояния
=i), i, j=1,2,..., r называются матрицами перехода из состояния 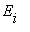 в состояние
в состояние 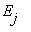 за один шаг.
за один шаг.
Цепь Маркова называется однородной, если вероятности перехода 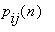 не зависят от n, т.е. если вероятности перехода не зависят от номера шага, а зависят только от того, из какого
не зависят от n, т.е. если вероятности перехода не зависят от номера шага, а зависят только от того, из какого
состояния и в какое осуществляется переход. Для однородных цепей Маркова вместо
будем писать 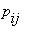 .
.
Вероятности перехода удобно располагать в виде квадратной матрицы
Матрица P называется матрицей вероятностей перехода однородной цепи Маркова за один шаг. Она обладает следующими свойствами:
1

а) 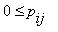 ;
;
б) для всех i 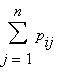 =1.
=1.
Квадратные матрицы, для которых выполняются условия а) и б), называются стохастическими.
ектор |
, где |
=P( |
), i=1,2...,r, называется вектором начальных |
вероятностей. |
|
|
|
Свойства однородных цепей Маркова полностью определяются вектором начальных вероятностей и матрицей вероятностей перехода. В конкретных случаях для описания эволюции цепи Маркова вместо явного выписывания матрицы P используют граф, вершинами которого являются
состояния цепи, а стрелка, идущая из состояния 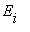 в состояние
в состояние 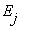 с числом
с числом 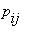 над ней показывает, что из состояния
над ней показывает, что из состояния 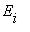 в состояние
в состояние 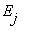 возможен переход с вероятностью
возможен переход с вероятностью 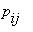 . В том
. В том
случае, когда  , соответствующая стрелка не проводится.
, соответствующая стрелка не проводится.
Можно показать, что матрица вероятностей перехода цепи Маркова за n шагов равняется n-ой степени матрицы P вероятностей перехода за один шаг.
Для однородной цепи Маркова при любом m выполняется равенство
P( 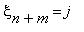 |
|  )=P(
)=P( 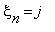 |
| 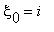 ).
).
Но последняя вероятность есть вероятность перехода из состояния  в состояние
в состояние 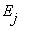 за n шагов.
за n шагов.
Теорема о предельных вероятностях . Если при некотором  все элементы матрицы
все элементы матрицы 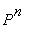 =[
=[
 ] положительны, то существуют пределы
] положительны, то существуют пределы
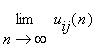 =
= 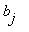 , i,j=1,2,...,r.
, i,j=1,2,...,r.
Предельные вероятности 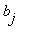 не зависят от начального состояния
не зависят от начального состояния 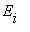 и являются единственным решением системы уравнений
и являются единственным решением системы уравнений
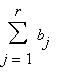 =1,
=1,
= 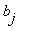 , j=1, 2, ..., r.
, j=1, 2, ..., r.
Физический смысл этой теоремы заключается в том, что вероятности нахождения системы в
состоянии 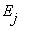 практически не зависит от того, в каком состоянии она находилась в далеком прошлом.
практически не зависит от того, в каком состоянии она находилась в далеком прошлом.
2

Цепь Маркова, для которой существуют пределы 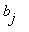 , называется эргодической.
, называется эргодической.
Решение ( 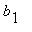 ,
, 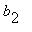 ,...,
,...,  ) написанной выше системы называется стационарным распределением вероятностей для марковской цепи с матрицей перехода P=[
) написанной выше системы называется стационарным распределением вероятностей для марковской цепи с матрицей перехода P=[ 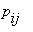 ].
].
Если из состояния  система может перейти в состояние
система может перейти в состояние 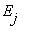 с положительной вероятностью за конечное число шагов, то говорят, что
с положительной вероятностью за конечное число шагов, то говорят, что 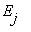 достижимо из
достижимо из 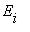 .
.
Состояние 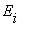 называется существенным, если для каждого состояния
называется существенным, если для каждого состояния 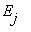 , достижимого из
, достижимого из 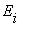 ,
,
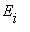 достижимо из
достижимо из 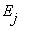 . Если же для хотя бы одного j
. Если же для хотя бы одного j  достижимо из
достижимо из 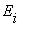 , а
, а 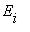 не достижимо
не достижимо
из 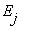 , то
, то 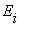 - несущественное состояние.
- несущественное состояние.
Задача 1 . Матрица вероятностей перехода цепи Маркова имеет вид
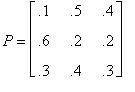 . Распределение по состояниям в момент времени t=0 определяется вектором
. Распределение по состояниям в момент времени t=0 определяется вектором
 . Найти:
. Найти:
1)распределение по состояниям в момент t=2;
2)вероятность того, что в моменты t=0, 1, 2, 3 состяниями цепи будут соответственно 1, 3, 3, 2;
3)стационарное распределение.
Решение. Зададим матрицу P, вектор начальных вероятностей q и найдем матрицу P2
вероятностей перехода за два шага как 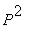 :
:
> P:=array([[0.1, 0.5, 0.4], [.6, .2, .2], [.3, .4, .3]]);q:=array([.7,.2,.1]); P2:=linalg[multiply](P,P);
2) Найдем распределение по состояниям в момент t=2
> q2:=linalg[multiply](q,P2);
Найдем распределение по состояниям в момент t=1
> q1:=linalg[multiply](q,P);
Найдем распределение по состояниям в момент t=3
> P3:=linalg[multiply](P,P,P):q3:=linalg[multiply](q,P3);
Тогда искомую вероятность найдем так
> P:=q[1]*q1[3]*q2[3]*q3[2];
3

Здесь мы перемножили первую координату вектора q (вероятность того, что система в начальный момент времени находилась в состоянии 1), третью координату вектора q1 (вероятность того, что система в момент времени t=1 находилась в состоянии 3), третью координату вектора q2 (вероятность того, что система в момент времени t=2 находилась в состоянии 3), вторую координату вектора q3 (вероятность того, что система в момент времени t=3 находилась в состоянии 2).
3) Найдем стационарное распределение цепи Маркова. Для этого транспонируем матрицу P
> P:=linalg[matrix]([[0.1, 0.5, 0.4], [.6, .2, .2], [.3, .4, .3]]);Pt:=linalg[transpose](P);
Для нахождения собственного собственного вектора транспонированной матрицы, сумма координат которого равняется 1, составим систему линейных уравнений
>
syst:={sum(Pt[1,k]*v[k],k=1..3)=v[1],sum(Pt[2,k]*v[k],k=1..3)=v[2],sum(Pt[3,k]*v[k],k=1..3)=v[3],s um(v[k],k=1..3)=1};
Решим эту систему
> solve(syst);
Таким образом, вектор v определяет стационарное распределение цепи Маркова.
Задача 2 . Пусть  - номер состояния в цепи Маркова в момент времени t, P(
- номер состояния в цепи Маркова в момент времени t, P(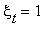 )=1 и
)=1 и
матрица вероятностей перехода за единицу времени равна 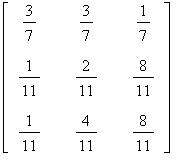 ;
; 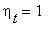 ,
,
если 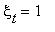 и
и 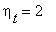 , если
, если 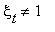 . Показать, что последовательность
. Показать, что последовательность 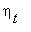 является цепью Маркова. Найти соответствующую ей матрицу вероятностей перехода.
является цепью Маркова. Найти соответствующую ей матрицу вероятностей перехода.
Задача 3 . Игральная кость все время перекладывается случайным образом с одной грани равновероятно на любую другую из четырех соседних граней независимо от предыдущего. К какому пределу стремится при t стремящемся к бесконечности вероятность того, что в момент времени t кость лежит на грани "6", если в момент t=0 она находилась в этом же положении (t=0,
1, 2, 3, ...)?
4
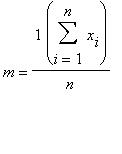
Задача 4 . Матрица вероятностей перехода P и вектор q начального распределения по состояниям имеют вид:
 ,
,
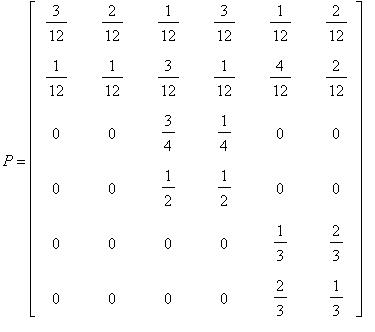 .
.
Найти:
а) несущественные состояния;
б) математическое ожидание 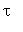 - времени выхода из несущественных состояний;
- времени выхода из несущественных состояний;
в) вероятности 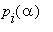 ,
, 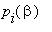 попадания в множества состояний
попадания в множества состояний 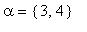 ,
, 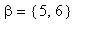 , если начальным состоянием является i из {1, 2};
, если начальным состоянием является i из {1, 2};
г) предельное при 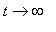 распределение по состояниям, т.е. величины
распределение по состояниям, т.е. величины 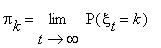 .
.
Задание 2. Точечные оценки неизвестных параметров распределения
Пусть 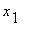 ,
, 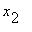 ,...,
,...,  - наблюдавшиеся значения случайной величины . Точечной оценкой для служит выборочное среднее
- наблюдавшиеся значения случайной величины . Точечной оценкой для служит выборочное среднее
Оценкой дисперсии является выборочная дисперсия
5

Для оценки дисперсии при малых n используется величина (исправленная выборочная дисперсия)
Корень квадратный из выборочной дисперсии называется выборочным средним квадратическим отклонением величины
.
(См. задачи в Агапов Г. И. Задачник по теории вероятностей: Учеб. пособие для студентов втузов. - М.: Высш. шк.,
1986.
Задача 1 . В результате пяти измерений длины стержня одним прибором (без систематических ошибок, т.е.
предполагается, что математическое ожидание измерений 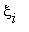 совпадает с истинной длиной стержня) получены следующие результаты ( в мм): 92, 94, 103, 105, 106. Найти:
совпадает с истинной длиной стержня) получены следующие результаты ( в мм): 92, 94, 103, 105, 106. Найти:
а) выборочную среднюю длину стержня; б) выборочную дисперсию и несмещенную оценку дисперсии ошибок прибора.
Решение . Загрузим библиотеку и зададим выборку
>with(stats);
>data:=[92,94,103,105,106];
Найдем выборочную среднюю, для чего используем команду mean из подбиблиотеки describe:
> describe[mean](data);
Найдем выборочную дисперию
> describe[variance](data);
Найдем несмещенную оценку дисперсии ошибок прибора:
> n/(n-1)*describe[variance](data);
Задача 2 . Приведены результаты измерения роста (в см) случайно отобранных 100 студентов
>
data:=[Weight(154..158,10),Weight(158..162,14),Weight(162..166,26),Weight(166..170,28),Weight(170..174, 12),Weight(174..178,8),Weight(178..182,2)];
Найти выборочное среднее и выборочную дисперсию роста обследованных студентов.
Задача 3 . На телефонной станции производились наблюдения за числом неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты:
>
data:=[3,1,3,4,2,1,1,3,2,7,2,0,2,4,0,3,0,2,0,1,3,3,1,2,2,0,2,1,4,3,4,2,0,2,3,1,3,1,4,2,2,1,2,5,1,1,0,1,1,2,1,0,3,4,1,
2,2,1,1,5]:
Найти среднее и дисперсию распределения. Сравнить с распределением Пуассона. Решение . Найдем выборочную среднюю
> lambda:=describe[mean](data);
Найдем выборочную дисперсию
> nu[2]:=describe[variance](data);
Представим выборку в виде статистического ряда:
6

> data1:=transform[tally](data);
Найдем относительные частоты
> data2:=transform[scaleweight[1/describe[count](data1)]](data1);
Вычислим соответствующие вероятности по формуле Пуассона
> data3 := array(1..7):
for i from 1 to 7 do data3[i] :=evalf(exp(-lambda)*lambda^(i-1)/(i-1)!) od: > print(data3);
Для сравнения относительных частот и вероятностей получим массив относительных частот
> data4:=transform[frequency](data2);
Сравним частоты и вероятности (в %)
> sum(abs(data3[k]-data4[k]),k=1..7)*100;
Очевидно, что относительные частоты мало отличаются от вероятностей. Поэтому распределение случайной величины (числа неправильных соединений в минуту) близко к распределению Пуассона.
Задача 3 . Измерен параметр транзистора, результаты измерений приведены в массиве
> data:=[4.4,4.31,4.4,4.4,4.65,4.56,4.71,4.54,4.34,4.56,4.32,4.42,4.6,4.35,4.5,4.4,4.43,4.48,4.42,4.45]:
Найти выборочную среднюю, выборочную дисперсию и ее несмещенную оценку.
Задача 4 . Измерительным прибором, практически не имеющим систематической погрешности, было сделано пять независимых измерений некоторой величины. Результаты измерений приведены в массиве
> data:=[2781,2836,2807,2763,2858]:
а) Найти выборочную дисперсию погрешности измерения, если измеряемая величина точно известна: 2800; б) найти выборочное среднее, выборочную дисперсию и ее несмещенную оценку, если точное значение измеряемой величины неизвестно.
Задача 5 . При шприцевании в лабораторных условиях протекторной резиновой смеси были получены следующие значения усадки: 90, 93.1, 95, 96, 100, 101, 106. Найти выборочное среднее значение усадки, выборочную дисперсию и ее несмещенную оценку.
Задание 3. Ковариация и коэффициент корреляции
Определение. Пусть и -случайные величины, - их произведение, M , M ,M - математические ожидания
этих величин, , - средние квадратические отклонения случайных чисел и . Число
называется коэффициентом ковариации случайных чисел и , а число
коэффициентом корреляции.
Свойства коэффициента корреляции:
1.r( , )=0 для независимых случайных величин и .
2.-1<=r( , )<=1 для любых случайных величин и .
3.Если |r( , )|=1, то случайные величины и связаны соотношением = a +b , где a и b - некоторые постоянные (если r( , )=1, то a>0, если r( , )= -1, то a<0).
Обратно, если и связаны соотношением 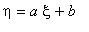 , то |r( , )|=1 (r( , )=1 при a>0, r( , )= -1 при a<0).
, то |r( , )|=1 (r( , )=1 при a>0, r( , )= -1 при a<0).
Справедливы следующие формулы: k( , )=M[( -M )( -M )],
7
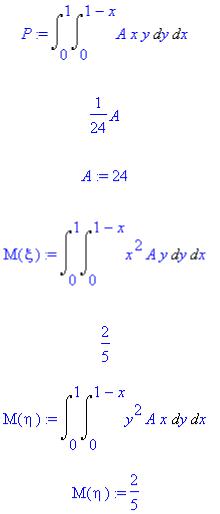
r( , )= 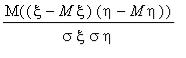 ,
,
k( , )= 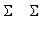 (
( 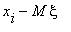 )(
)( 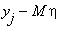 )
) 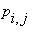 ,
,
k( , )= 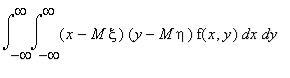 .
.
Задача 1 . (Агапов Г. И. Задачник по теории вероятностей: Учеб. пособие для студентов втузов. - М.: Высш. шк.,
1986.) Двумерная случайная величина ( ) подчинена закону распределения с плотностью вероятности f(x,y)=Axy в области D и f(x,y)=0 вне этой области. Область D - треугольник, ограниченный прямыми x+y-1 =0, x=0, y=0. Найти: а) величину А;
б) M и M ;
в)D и D ;
г) k( , );
д) r( ) .
Решение . а) Очевидно, что двойной интеграл по области D от функции f(x,y) есть вероятность попадания случайной точки в область D. Загрузим библиотеку student
> with(student):f(x,y):=A*x*y:
Выразим вероятность попадания случайной точки в область D через инертную форму двойного интеграла:
> P:=Doubleint(f(x,y),y=0..1-x,x=0..1);
Оценим инертную форму:
> value(P);
Очевидно, что P=1. Тогда
> A:=24;
б) Найдем математические ожидания случайных величин и :
> M(xi):=Doubleint(x*f(x,y),y=0..1-x,x=0..1);
Оценим математическое ожиданиеM :
>value(M(xi));
>M(eta):=Doubleint(y*f(x,y),y=0..1-x,x=0..1);
>M(eta):=value(M(eta));
Таким образом, математические ожидания случайных величин и равны 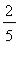 . в) Вычислим дисперсии случайных величин и :
. в) Вычислим дисперсии случайных величин и :
8

>D(xi):=value(Doubleint((x-M(xi))^2*f(x,y),y=0..1-x,x=0..1));
>D(eta):=value(Doubleint((y-M(eta))^2*f(x,y),y=0..1-x,x=0..1));
г) Найдем ковариацию и коэффициент корреляции:
>k(xi,eta):=value(Doubleint((y-M(eta))*(x-M(xi))*f(x,y),y=0..1-x,x=0..1));
>r(xi,eta):=k(xi,eta)/(sqrt(D(xi)*D(eta)));
(Задачи 2, 3 и 4 из Чистяков В. П. Курс теории вероятностей: Учеб.-3-е изд., испр.-М.: Наука. Гл. ред. физ.-мат. лит.- 1987.)
Задача 2 . Дано совместное распределение случайных величин и :
> matr:=linalg[matrix](3,7,[xi, -1, -1, 0, 0, 1,1,eta, -1, 1, -1, 1, -1,1,p, 1/8, 5/24, 1/12, 1/6, 7/24,1/8]);
Найти:
а) одномерные законы распределения и ; б) закон распределения ; в) закон распределения 2 ;
г) ковариацию и коэффициент корреляции и .
Задача 3 . Совместное распределение случайных величин и определяется формулами 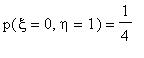 ,
,
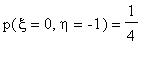 ,
, 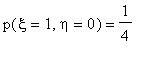 ,
, 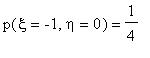 . Найти
. Найти
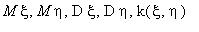 . Являются ли и независимыми величинами?
. Являются ли и независимыми величинами?
Задача 4 . Случайные величины 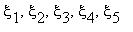 независимы;
независимы; 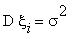 . Найти коэффициент корреляции величин
. Найти коэффициент корреляции величин
а) 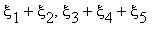 ;
;
б)  .
.
Задание 4. Элементы корреляционного анализа
Цель решения задач : обработка результатов наблюдения для построения линейного приближения методом наименьших квадратов и для нахождения корреляционной зависимости между случайными величинами. В результате решения задач требуется получить выборочное уравнение прямой регрессии Y на X:
9

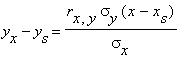 , где
, где  - выборочные средние Y и X, соответственно,
- выборочные средние Y и X, соответственно, 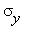 ,
, 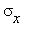 - средние
- средние
квадратичные отклонения Y и X, 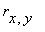 - коэффициент корреляции между X и Y.
- коэффициент корреляции между X и Y.
Задача 1 . Пусть X- динамическая нагрузка вагона рабочего парка, а Y - себестоимость перевозок, n - частота (X, Y).
Дана выборка (X, Y, n): {(28, 3, 1), (28, 3.5, 3), (30, 3, 2), (32, 2, 1), (32, 2.5, 2), (32, 3, 1), (34, 2, 1), (34, 2.5, 2), (36,
2.5, 2)}. Найти уравнение прямой регрессии Y на X.
Решение : Загрузим библиотеку stats и зададим X и Y с соответствующими частотами:
>with(stats):
>X:=[28,Weight(28,3),Weight(30,2),32,Weight(32,2),32,34,Weight(34,2),Weight(36,2)];
>Y:=[3,Weight(3.5,3),Weight(3,2),2,Weight(2.5,2),3,2,Weight(2.5,2),Weight(2.5,2)];
Найдем выборочные средние X и Y:
>Xsr:=describe[mean](X);
>Ysr:=describe[mean](Y);
Вычислим стандартные отклонения X и Y:
>sigmaX:=describe[standarddeviation](X);
>sigmaY:=describe[standarddeviation](Y);
Найдем коэффициент корреляции:
> r[x,y]:=describe[linearcorrelation](X,Y);
Составим уравнение прямой регрессии Y на X:
> y-Ysr=evalf(r[x,y]*sigmaY/sigmaX)*(x-Xsr);
Всилу того, что модуль коэффициента корреляции значительно отличается от 1, между X и Y нет линейной зависимости. Из отрицательности коэффициента корреляции следует, что при возрастании X наблюдается убывание Y.
Вследующих задачах получить выборочное уравнение прямой регрессии Y на X. Сделать вывод о характере и тесноте связи между X и Y.
Задача 2. Пусть X- стоимость активной части производственных фондов, млн. руб., Y - выработка продукции на одного рабочего, тыс. руб., n - частота наблюдений (X, Y). Имеется выборка (X, Y, n): {(10, 0.8, 3), (10.5, 0.8, 2), (10.5, 1, 2), (11, 0.8, 1), (11, 1, 2), (11, 1.2, 2), (11, 1.4, 1), (11.5, 1, 1), (11.5, 1.2, 1), (11.5, 1.4, 1), (12, 1.2, 2), (12, 1.4, 2)}.
Задача 3 . Пусть X- производительность труда, тысяч единиц, Y - себестоимость единицы продукции, руб., n - частота наблюдений (X, Y). Имеется выборка (X, Y, n): {(11,13, 2), (11, 15, 2), (13, 11, 3), (13, 13, 4), (13, 15, 1), (15, 7, 1),
(15, 9, 3), (15, 11, 7), (15, 13, 5), (17, 7, 1), (17, 9, 4), (17, 11, 4), (19, 7, 2), (19, 9, 1)}.
Задача 4 . Пусть X- количество типичных дефектов, Y - срок службы ходовых частей вагона, лет, n - частота наблюдений (X, Y). Имеется выборка (X, Y, n): {(0,1, 35), (0, 3, 15), (5, 1, 12), (5, 3, 34), (5, 5, 5), (10, 3, 6), (10, 5,
11), (15, 5, 3), (15, 7, 2), (20, 5, 1)}.
Задача 5 . Пусть X- средняя величина доходной ставки, руб., Y - доход от перевозок, млн. руб., n - частота наблюдений (X, Y). Дана выборка (X, Y, n): {(2.3, 7.1, 5), (2.3, 7.3, 4), (2.6, 7.3, 12), (2.6, 7.5, 8), (2.6, 7.7, 1), (2.9, 7.5, 5), (2.9, 7.7, 5), (3.2, 7.5, 4), (3.2, 7.7, 7), (3.5, 7.7, 2), (3.5, 7.9, 2)}.
Задача 6 . Пусть X- товарооборот материально-технического обеспечения, млн. руб., Y - относительный уровень заготовительно-складских расходов, %, n - частота наблюдений (X, Y). Дана выборка (X, Y, n): {(5,10, 1), (5, 11, 6), (7,
10, 5), (7, 11, 6), (9, 9, 5), (9, 10, 3), (9, 11, 1), (11, 8, 4), (11, 9, 4), (13, 8, 3), (13, 9, 1)}.
Задача 7 . Пусть X- длина поезда, м., Y - масса поезда, брутто, т., n - частота наблюдений (X, Y). Дана выборка (X, Y, n): {(650, 2500, 8), (700, 2500, 9), (700, 3000, 11), (750, 3000, 13), (750, 3500, 19), (800, 3000, 1), (800, 3500, 24), (800, 4000, 28), (850, 3000, 4), (850, 3500, 22), (850, 4000, 31)}.
Задача 8 . Пусть X- густота перевозок, млн. т., Y - себестоимость перевозок, руб./10 тыс. ткм, n - частота наблюдений
(X, Y). Дана выборка (X, Y, n): {(10, 3.5, 5), (15, 3, 6), (20, 2.5, 5), (20, 3, 4), (25, 2.5, 3), (25, 3, 1), (30, 2, 2)}.
10
