Мои работы / Lab_7_Gorohov_IST-114

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Кафедра Информационных Управляющих Систем

ОТЧЁТ

по лабораторной работе №7 на тему: «Решение задачи регрессии с помощью нейронной сети»

по дисциплине «Теория информации, данные, знания»

Выполнили: студенты группы ИСТ-114, Горохов Д.Г., Калинько С.С.

«30» мая 2023 г. _______/ Горохов Д.Г. /

«30» мая 2023 г. _______/ Калинько С.С /

Принял: Эль Сабаяр Шевченко Н.

«__» ______ 2023 г. ______/ Эль Сабаяр Шевченко Н./

ЦЕЛЬ РАБОТЫ

Исследование принципов разработки нейронной сети на примере задачи регрессии.

ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ

1. Исследовать нейронную сеть при заданных начальных параметрах: метод оптимизации – SGD, число нейронов в скрытом слое – 20, шаг градиентного спуска – 0,01. Найти минимальное значение n_hidden_neurons, при котором сеть дает удовлетворительные результаты.

2. Найти наилучшее значение шага градиентного спуска lr в интервале от номинального значения.

3. Изменить нейронную сеть для предсказания функции y = 2^x * sin(2^−x)

4. Для этой задачи (п.3) получить метрику MAE = не хуже 0.03, варьируя: архитектуру сети, loss-функцию, lr оптимизатора или количество эпох в обучении.

ОПИСАНИЕ МЕТОДИКИ ИССЛЕДОВАНИЯ

В первую очередь нужно рассмотреть понятие регрессии. Регрессия –это односторонняя стохастическая зависимость, устанавливающая соответствие между случайными переменными, то есть математическое выражение, отражающее связь между зависимой переменной у и независимыми переменными х при условии, что это выражение будет иметь статистическую значимость. Фактически, задача регрессии – это предсказание некоторого вещественного числа. Для решения модельной задачи используем нейронную сеть c одним полно связным скрытым слоем, представленную на рис.1.

Рис.1. Схема нейронной сети с одним скрытым слоем

В данном задании нейронная сеть изначально состоит из 20 нейронов в скрытом слое (n_hidden_neurons). Чем больше нейронов, тем более сложные задачи способна решить нейронная сеть. Используется оптимизатор ADAM (который сочетает в себе идею накопления движения и идею более слабого обновления весов для типичных признаков), с шагом (learning rate) 0.001.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

При заданных начальных значениях гиперпараметров результат после обучения выглядит неудовлетворительно (рис.2).

Рис.2 – Начальные параметры

Минимальное значение количества скрытых нейронов, при котором сеть дает удовлетворительное значение 530.

Рис.3 – Значение в 530 нейронов

Если же уменьшить количество нейронов, например, до 500, результат будет хуже.

Рис.4 – Значение 500 нейронов

При изменении значения шага градиентного спуска lr в интервале от номинального значения (рис.5,6,7), получаем наилучший результат на шаге равном 0.01.

Рис.5 lr – 0.005

Рис.6 lr – 0.01

Рис.7 lr – 0.0109

Изменить нейронную сеть для предсказания функции y = 2x * sin(2−x).

def fun(x):

return (2**x)*torch.sin(2**(-x))

x_train = torch.linspace(-10, 5, 100)

y_train = fun(x_train)

noise = torch.randn(y_train.shape) / 20.

y_train = y_train + noise

x_train.unsqueeze_(1)

y_train.unsqueeze_(1)

x_validation = torch.linspace(-10, 5, 100)

y_validation = fun(x_validation.data)

x_validation.unsqueeze_(1)

y_validation.unsqueeze_(1)

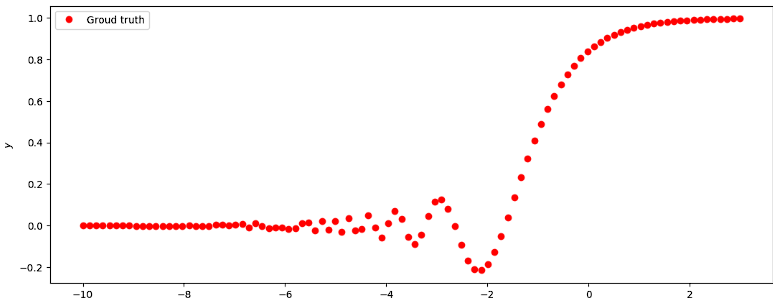
Рис.8 - График функции y = 2x * sin(2−x)

Получаем метрику MAE = , добавляя данные:

def metric(pred, target):

        return (pred - target).abs().mean()

print(metric(sine_net.forward(x_validation), y_validation).item())

Рис.9 – Нейронов - 750, Эпох – 12000, lr – 0.0089

ВЫВОД

В результате проведения лабораторной работы были исследованы принципы разработки нейронной сети на примере задачи регрессии.

КОД

import torch

import matplotlib.pyplot as plt

import matplotlib

matplotlib.rcParams['figure.figsize'] = (13.0, 5.0)

def fun(x):

return (2**x)*torch.sin(2**(-x))

def prepare_data():

x_train = torch.linspace(-10, 5, 100)

y_train = fun(x_train)

noise = torch.randn(y_train.shape) / 20.

y_train = y_train + noise

x_train.unsqueeze_(1)

y_train.unsqueeze_(1)

x_validation = torch.linspace(-10, 5, 100)

y_validation = fun(x_validation.data)

x_validation.unsqueeze_(1)

y_validation.unsqueeze_(1)

return x_train, y_train, x_validation, y_validation

class SineNet(torch.nn.Module):

def __init__(self, n_hidden_neurons):

super(SineNet, self).__init__()

self.fc1 = torch.nn.Linear(1, n_hidden_neurons)

self.act1 = torch.nn.Sigmoid()

self.fc2 = torch.nn.Linear(n_hidden_neurons, 1)

def forward(self, x):

x = self.fc1(x)

x = self.act1(x)

x = self.fc2(x)

return x

def predict(net, x, y):

y_pred = net.forward(x)

plt.plot(x.numpy(), y.numpy(), 'o', c='r', label='Groud truth')

plt.plot(x.numpy(), y_pred.data.numpy(), 'o', c='b', label='Prediction')

plt.legend(loc='upper left')

plt.xlabel('$x$')

plt.ylabel('$y$')

def loss(pred, target):

squares = (pred - target)**2

return squares.mean()

def train(net, x_train, y_train):

optimizer = torch.optim.SGD(net.parameters(), lr=0.0089)

for epoch_index in range(12000):

optimizer.zero_grad()

y_pred = net.forward(x_train)

loss_val = loss(y_pred, y_train)

loss_val.backward()

optimizer.step()

def metric(pred, target):

return (pred - target).abs().mean()

sine_net = SineNet(750)

x_train, y_train, x_validation, y_validation = prepare_data()

train(sine_net, x_train, y_train)

predict(sine_net, x_validation, y_validation)

print(metric(sine_net.forward(x_validation), y_validation).item())

САНКТ-ПЕТЕРБУРГ 2023