attachments_04-10-2012_21-18-24 / репетиционные тесты с теорией для ТиП (050502)

Образовательная программа: 050502.65 – Технология и предпринимательство

Дисциплина: Математика

Всего заданий: 30 (время – 60 минут)

www.fepo-nica.ru

вкладка ТЕСТИРОВАНИЕ  РЕПЕТИЦИОННОЕ ВУЗАМ  выбрать специальность и дисциплину.

; .

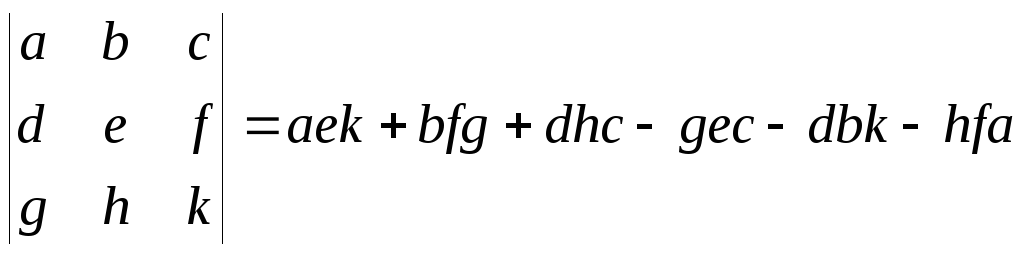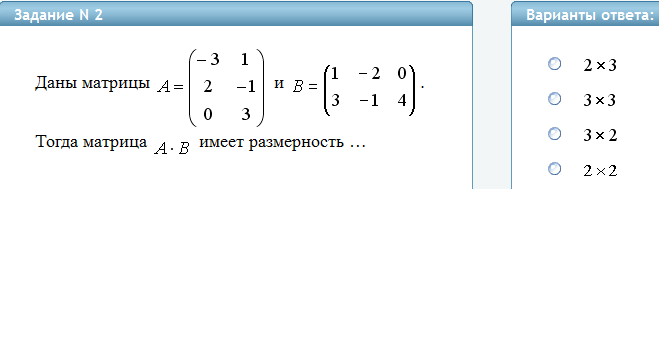
Произведением матриц , , и , , называется матрица , элементы которой равны произведению i-й строки матрицы А на j-й столбец матрицы В.

Для того, чтобы можно было выполнить умножение, число столбцов первой матрицы должно быть равным числу строк второй матрицы.

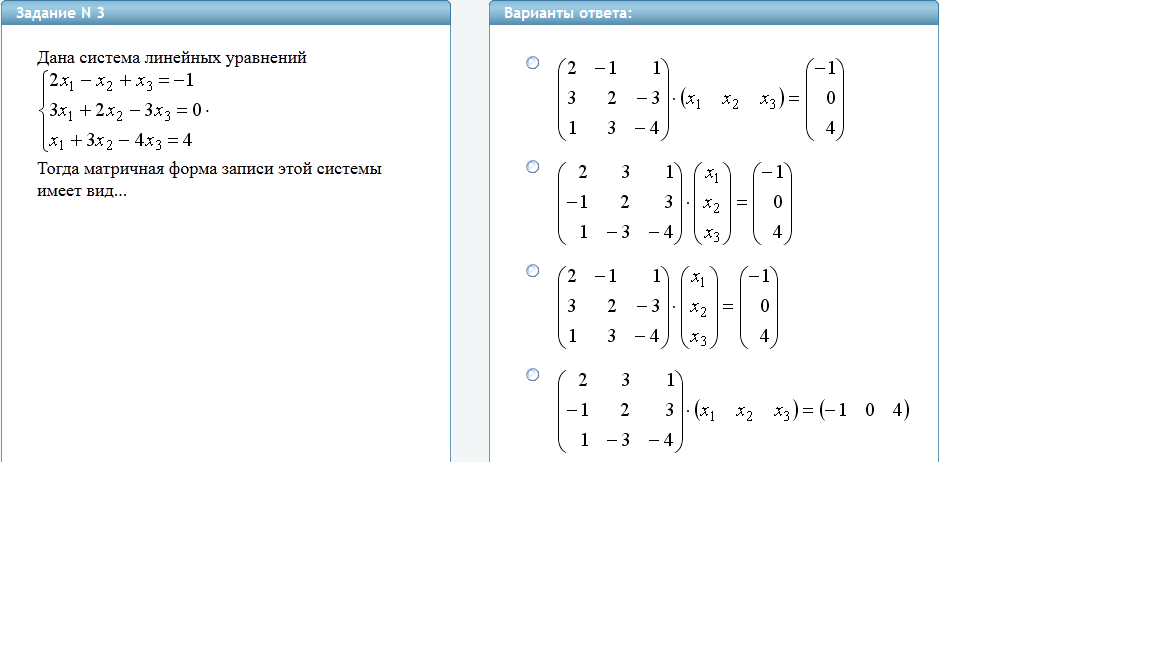
Пусть дана система линейных алгебраических уравнений

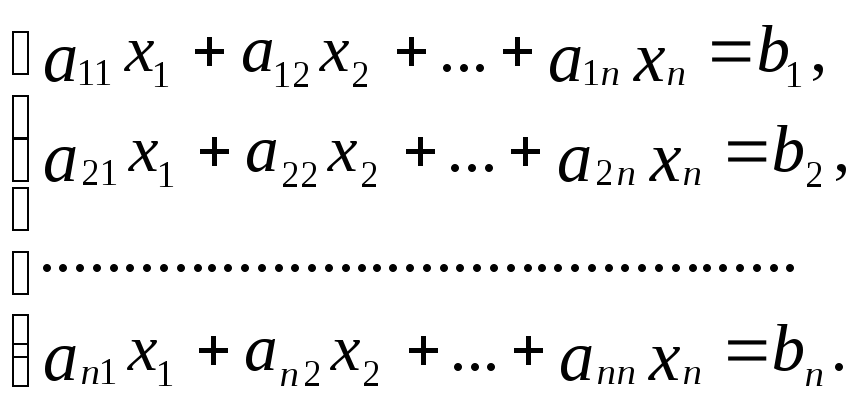
Матричная форма имеет вид: , где , , .

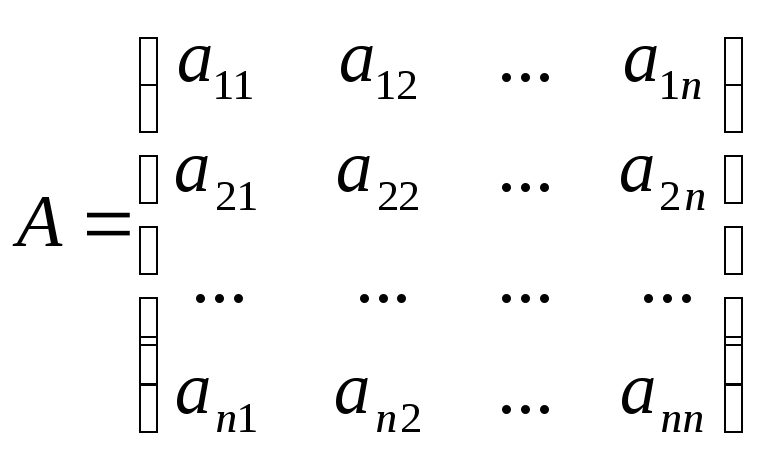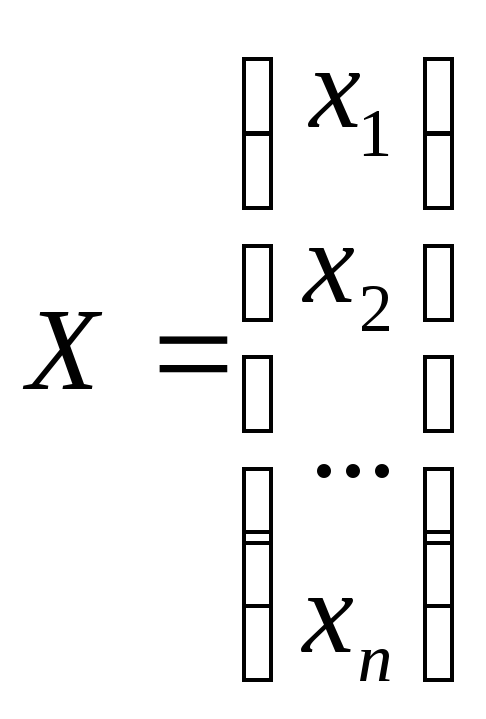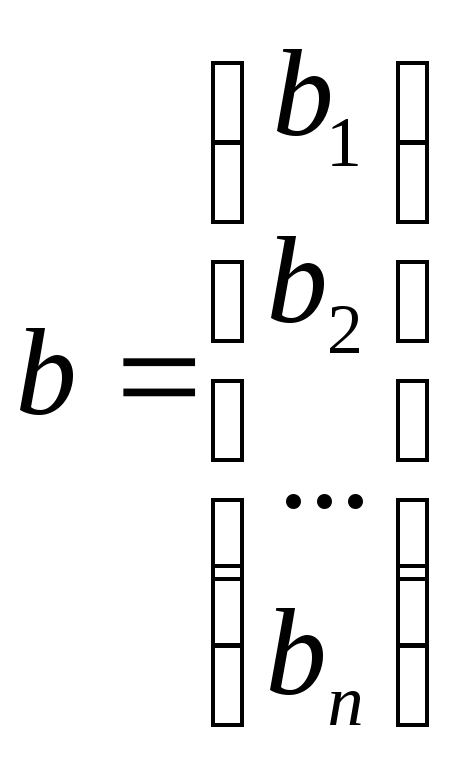Расширенной матрицей системы называется матрица, составленная из коэффициентов при неизвестных системы и свободных членов

.

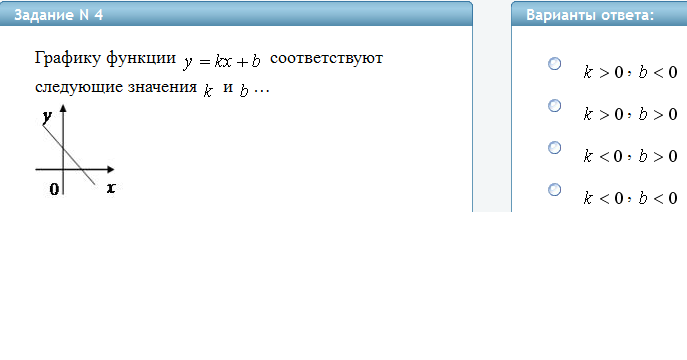
Геометрический смысл углового коэффициента прямой в ПДСК: угловой коэффициент прямой равен тангенсу направленного угла от базисного вектора оси абсцисс до направляющего вектора прямой: , где ).

Уравнение прямой , заданной точкой и угловым коэффициентом k:

, или , где .

Если прямая проходит через начало координат О, то , тогда: .

Если , то имеем

Если , то прямая возрастает, если , то прямая убывает.

Замечания.

1. Если прямые параллельны или совпадают, то их угловые коэффициенты равны: .

2. Угловые коэффициенты взаимно перпендикулярных прямых обратны по величине и противоположны по знаку: , то есть .

Канонические уравнения кривых второго порядка:

эллипс: , .

гипербола: , .

парабола: .

пара пересекающихся прямых: , или .

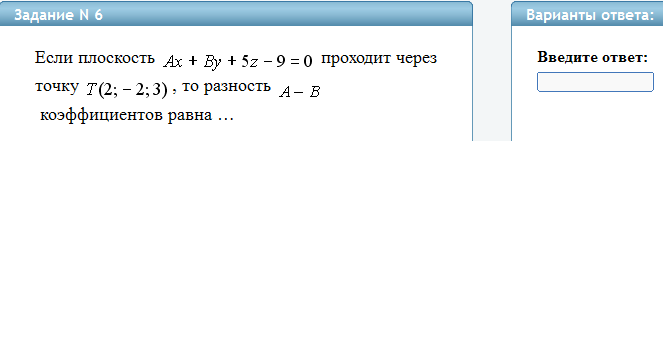
Плоскость задаётся общим уравнением

, где ,

вектор является нормальным вектором этой плоскости, т.е. .

Точка (координаты точки удовлетворяют уравнению плоскости).

Пусть функция определена на интервале , и – два произвольных значения аргумента из этого интервала: , . Обозначим , то есть .

Определение. Говорят, что для перехода от значения аргумента к значению первоначальному значению придано приращение .

Определение. Приращением функции , соответствующим приращению аргумента в точке , называется разность .

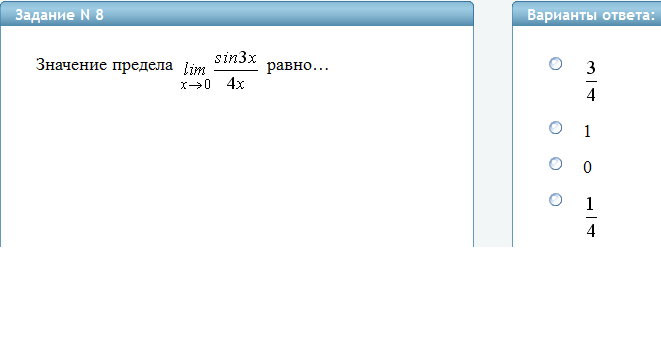
Некоторые замечательные пределы

Физический смысл производной: производная от пути по времени в точке есть мгновенная скорость точки в момент времени .

Пусть – закон движения материальной точки (движение прямолинейное); тогда

.

Аналогично, производная от скорости по времени в точке есть ускорение в момент времени :

.

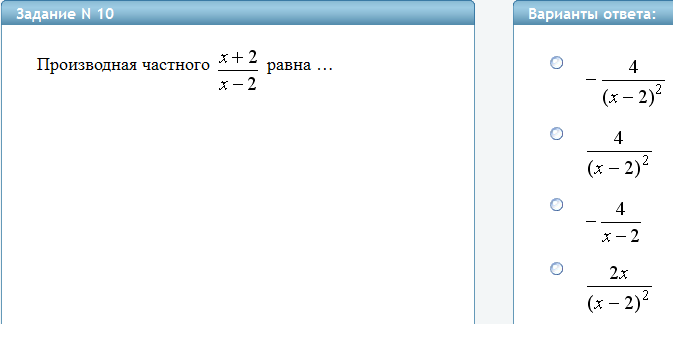
Правила дифференцирования:

1) ;

2) ; ;

3) .

Таблица производных

Производная параметрически заданной функции

Для вычисления производной неявной функции надо продифференцировать обе части уравнения, задающего эту функцию, считая, что зависит от , то есть . Затем из полученного после дифференцирования уравнения надо выразить .

Правило Лопиталя позволяет раскрывать неопределённости типа и .

или .

Если отношение производных опять представляет собой неопределённость вида , то можно снова применить правило Лопиталя, то есть перейти к отношению вторых производных и т.д.

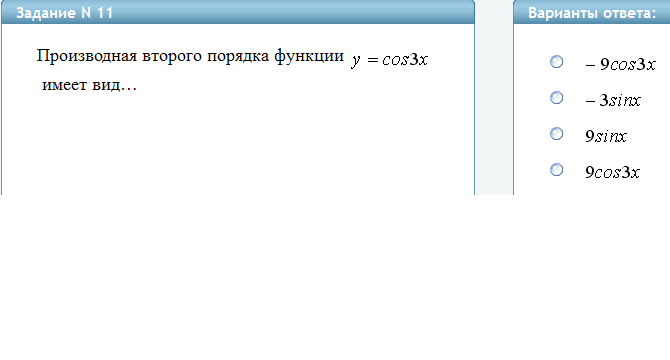
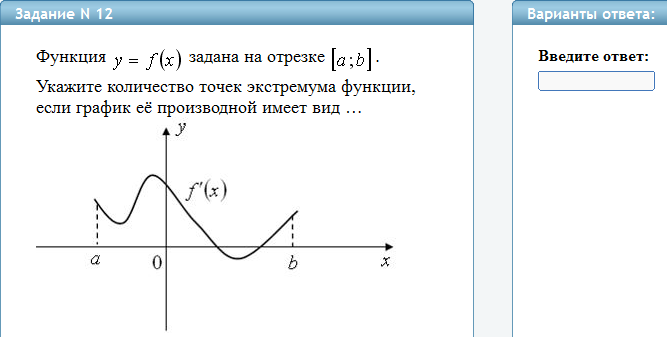
Теорема (признак постоянства функции на промежутке). Пусть функция определена и непрерывна на промежутке и дифференцируема на . Для того, чтобы была постоянной на , необходимо и достаточно выполнение равенства на .

Теорема (признак возрастания и убывания функции). Пусть функция определена и непрерывна на промежутке и дифференцируема на . Тогда для того, чтобы была возрастающей (убывающей) на необходимо и достаточно, чтобы () на .

Теорема (необходимое условие экстремума). Если является точкой экстремума функции , то в этой точке либо функция не дифференцируема, либо .

Теорема (достаточный признак экстремума). Пусть функция дифференцируема в некоторой окрестности точки , за исключением, может быть, самой точки , в которой она непрерывна. Тогда, если производная меняет знак при переходе через точку , то является точкой экстремума. Если при этом знак меняется с «+» на «–», то является точкой максимума, если же знак меняется с «–» на «+», то является точкой минимума. Если производная не меняет знака при переходе через точку , то точка не является точкой экстремума.

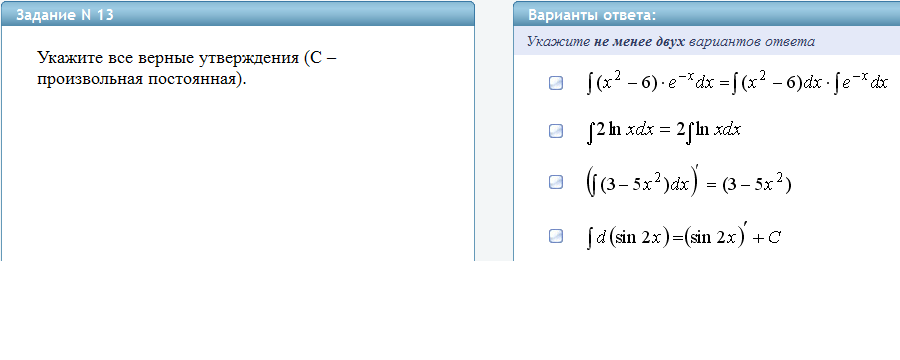
Определение. Функция называется первообразной для данной функции на промежутке , если выполняется равенство .

Определение. Выражение , где – первообразная функции и – произвольная постоянная, называется неопределённым интегралом от функции и обозначается символом , причём называется подынтегральной функцией, – подынтегральным выражением, – переменной интегрирования, ∫ – знак неопределённого интеграла. Таким образом, по определению

, если .

Свойства неопределённого интеграла

1) Производная неопределённого интеграла равна подынтегральной функции:

, или .

2) Дифференциал от неопределённого интеграла равен подынтегральному выражению:

.

3) Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

.

4) Постоянный множитель можно вынести за знак неопределённого интеграла:

.

5) Неопределённый интеграл от суммы двух функций равен сумме неопределённых интегралов от этих функций:

.

Таблица основных интегралов

,

Пусть функция определена на промежутке , и её переменная непрерывно дифференцируема на некотором промежутке . Тогда

, ;

. (1)

Формула (1) называется формулой замены переменной в неопределённом интеграле.

Пусть и – непрерывно дифференцируемые функции. Рассмотрим функцию , , откуда . Интегрируя, получим: , или

. (2)

Формула (2) есть формула интегрирования по частям.

Примечание. Пусть – многочлен n-ой степени.

– лучше принять , – всё, что осталось;

– , где – тригонометрические функции;

– ;

– , где – обратные тригонометрические функции.

Пусть функция непрерывна на отрезке . Если на , то площадь S криволинейной трапеции, ограниченной линиями , , , , равна интегралу