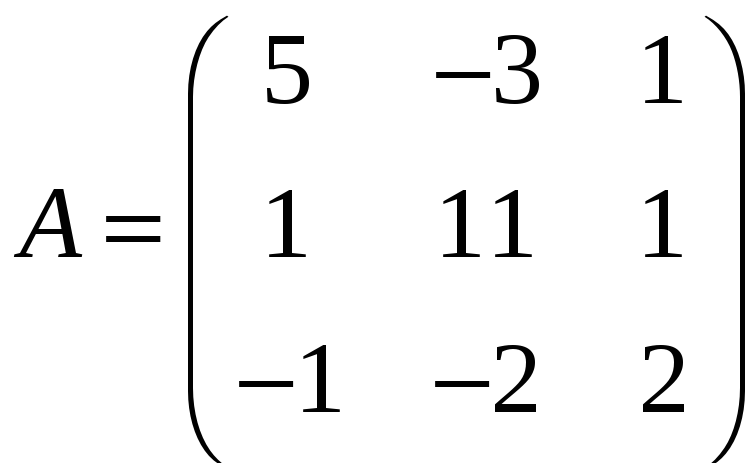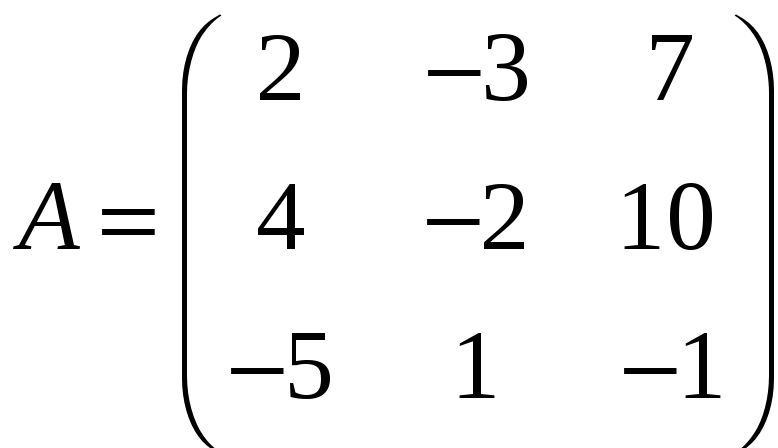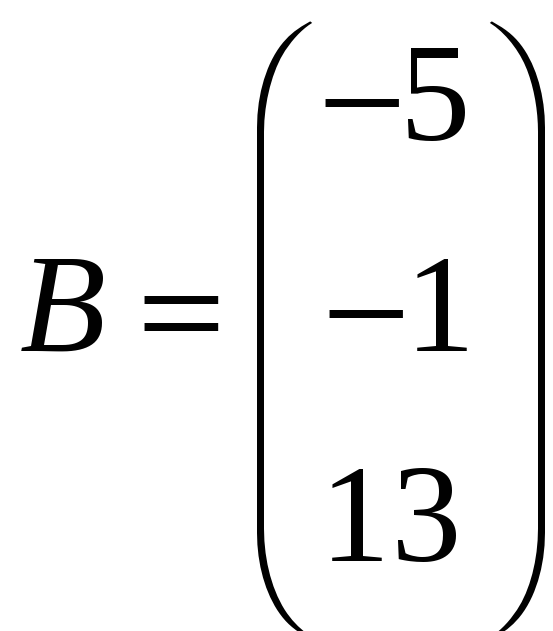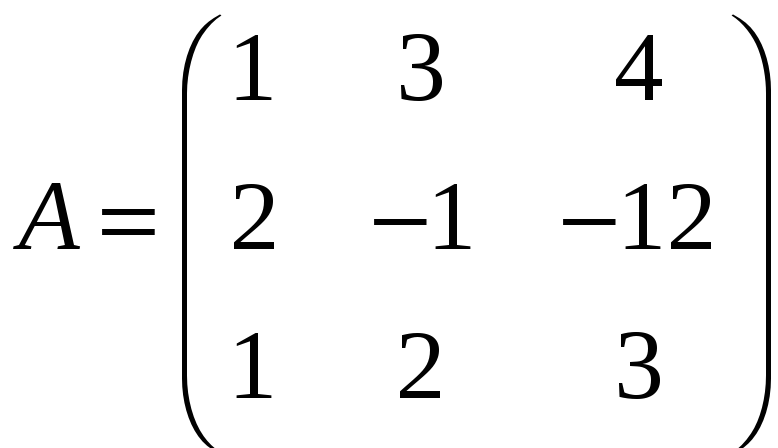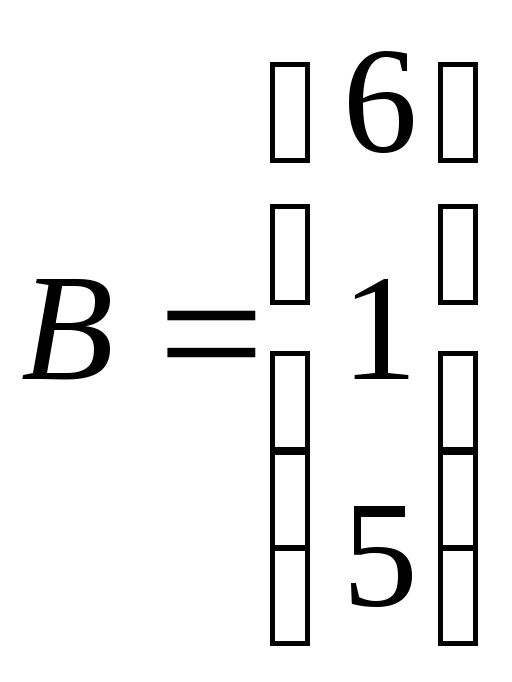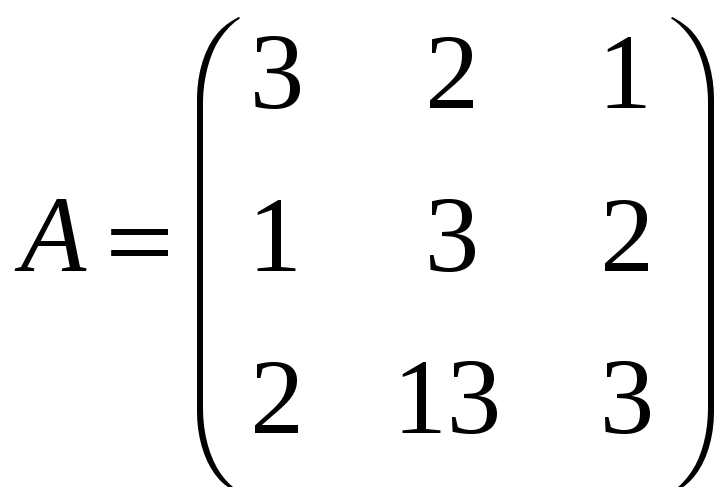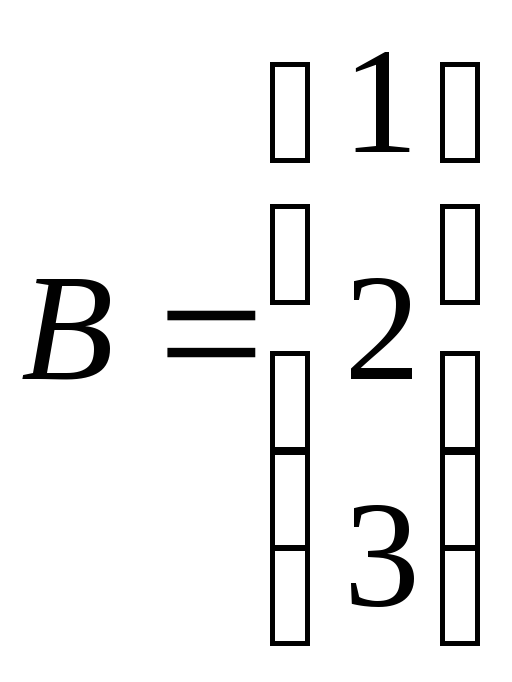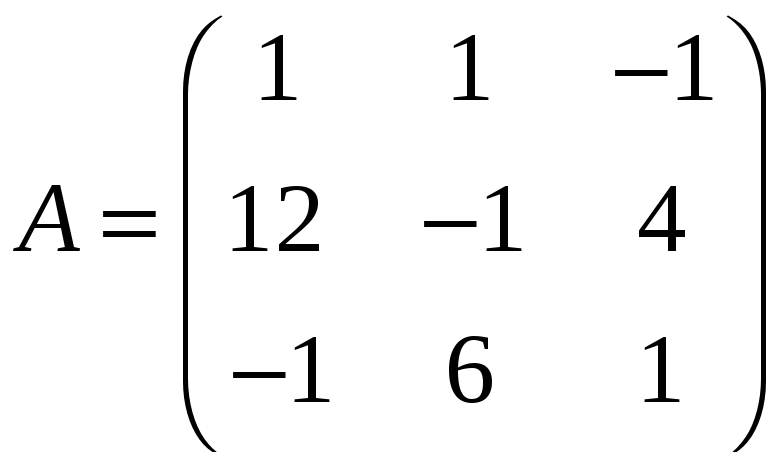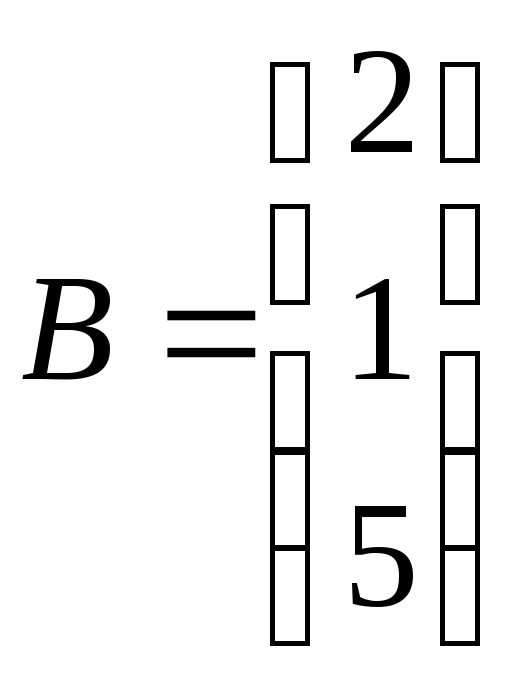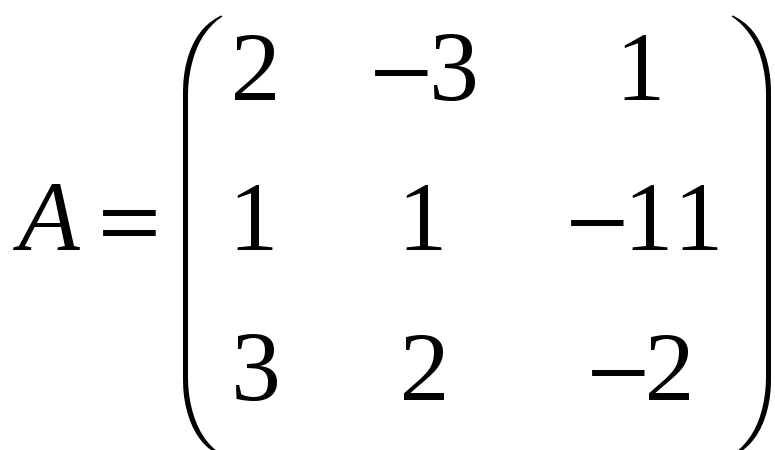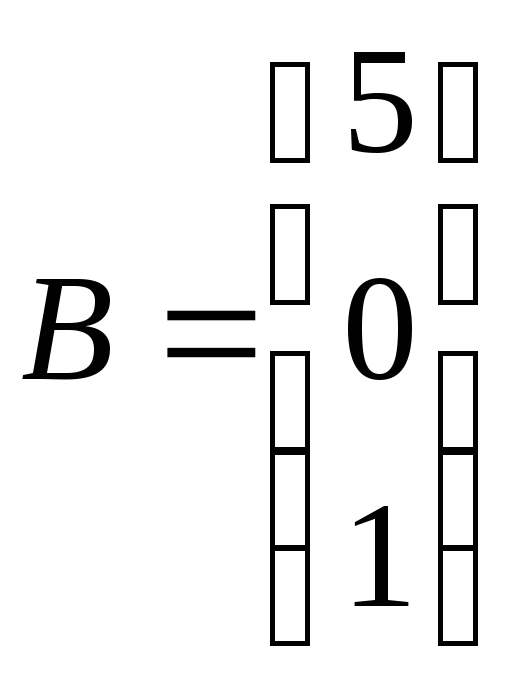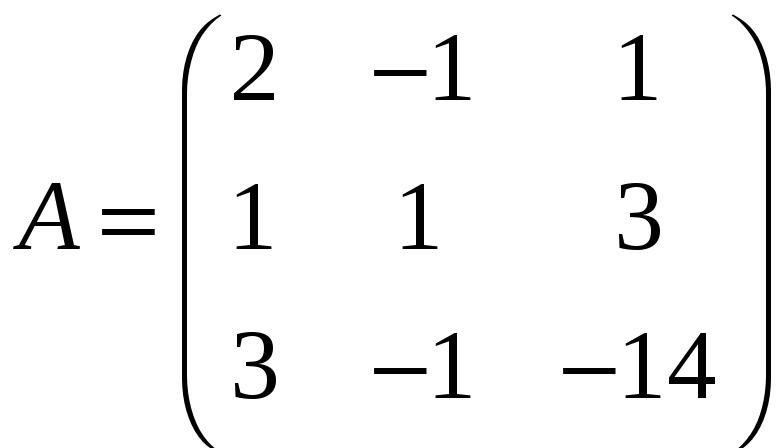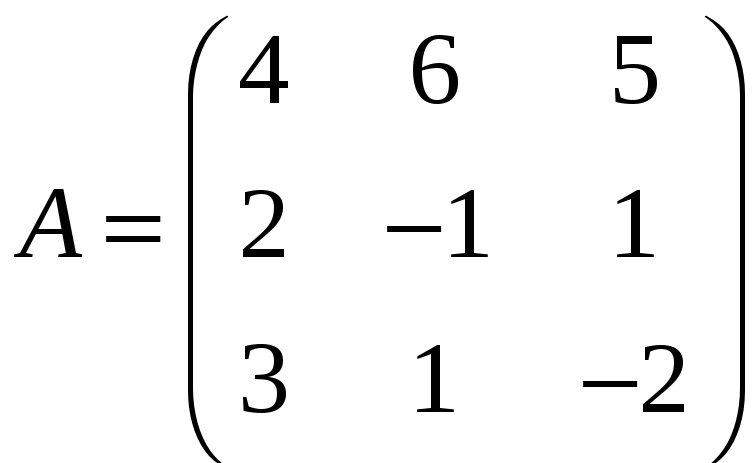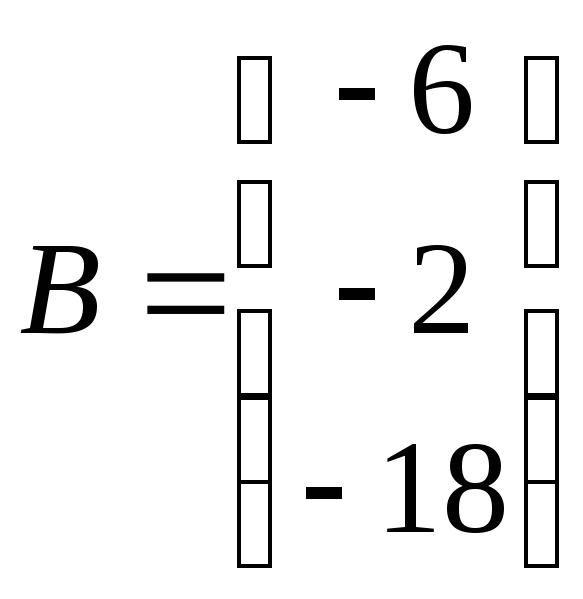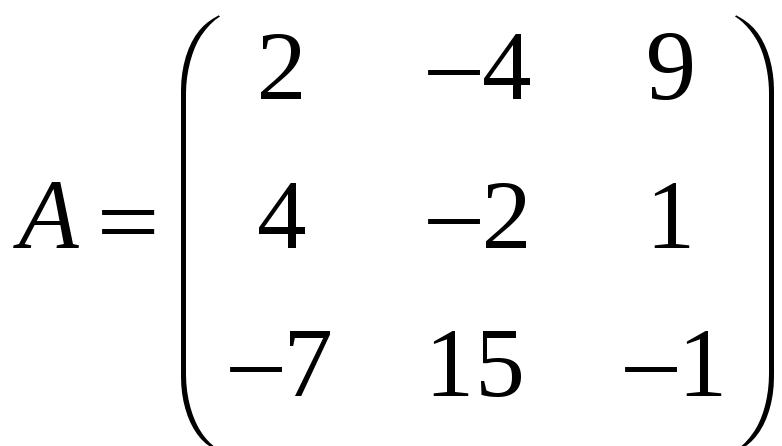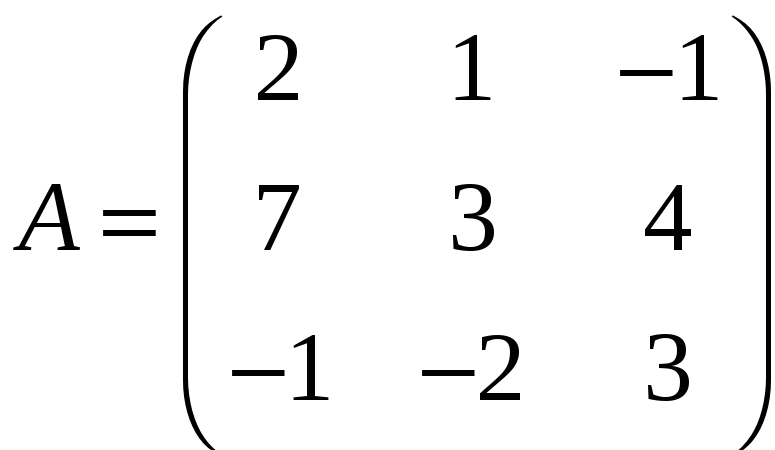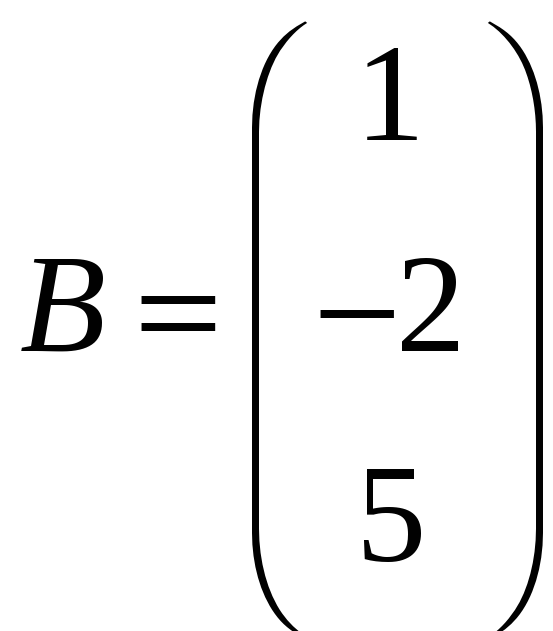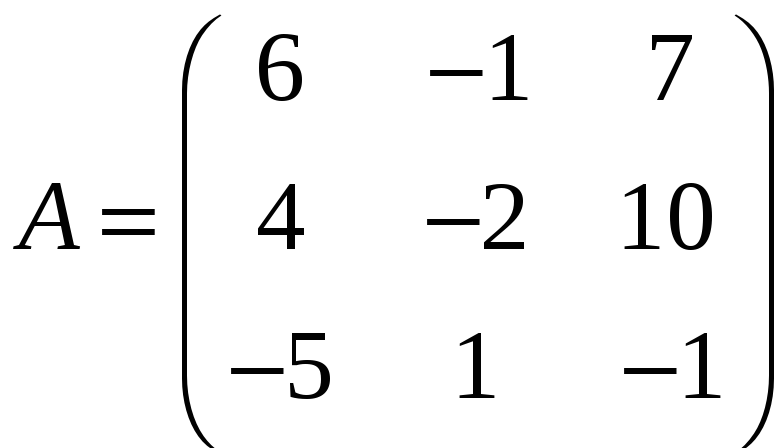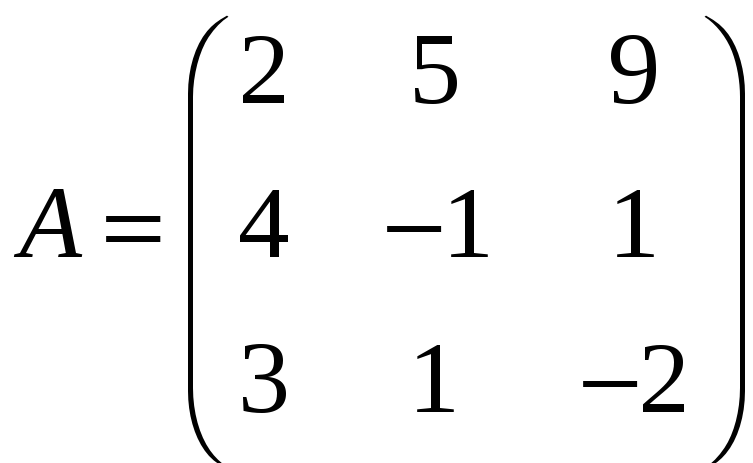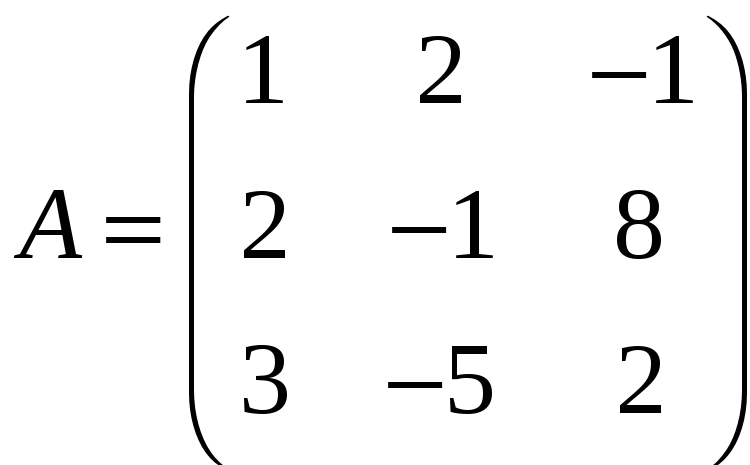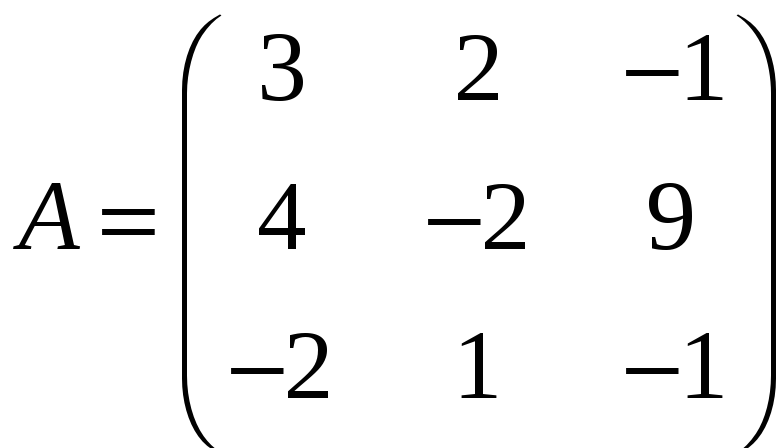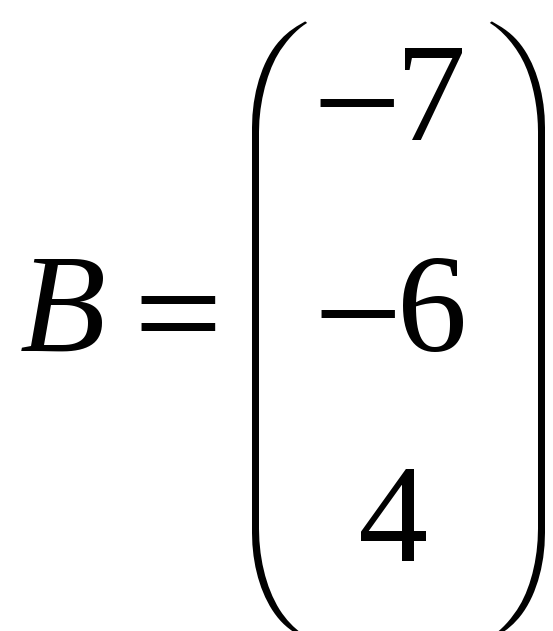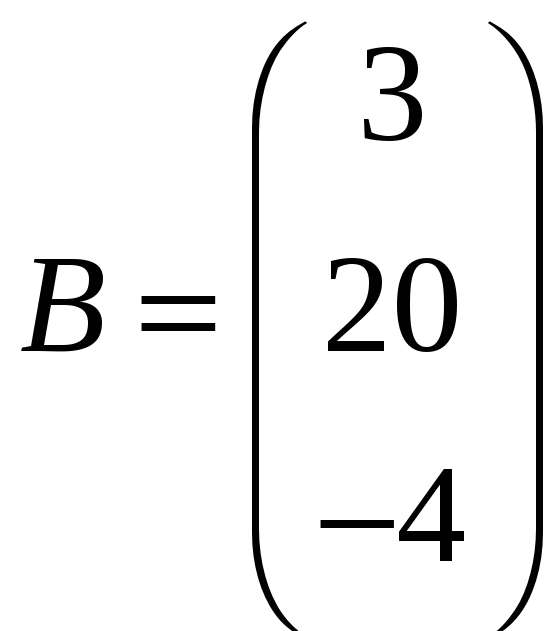ЛАБ MAPLE ИС / ЛАБ 1-2 решение систем линейных уравнений

6

ЛАБОРАТОРНАЯ РАБОТА № 1-2

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

******************************************************************************

1. МЕТОД КРАМЕРА.

Зададим систему уравнений с помощью матрицы системы А и вектора свободных членов В.

> restart:

> with(linalg):

> A:=<<5,1,-1>|<-3,1,-2>|<1,1,2>>;

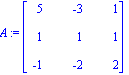
> B:=<14,2,2>;

Найдем главный определитель системы:

> det(A);

Найдём частные определители заменой соответствующего столбца на столбец свободных членов:

> A1:=<<14,2,2>|<-3,1,-2>|<1,1,2>>;

A2:=<<5,1,-1>|<14,2,2>|<1,1,2>>;

A3:=<<5,1,-1>|<-3,1,-2>|<14,2,2>>;

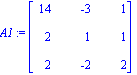
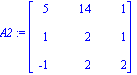
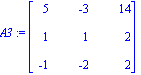
> det(A1);det(A2);det(A3);

Найдём неизвестные по теореме Крамера:

> x:=det(A1)/det(A); y:=det(A2)/det(A); z:=det(A3)/det(A);

ЗАДАНИЕ.

а) Перемножить матрицы А1 и А2. Найти определитель полученной матрицы и убедиться в том, что он равен произведению det(A1) и det(A2).

б) Решить систему своего варианта методом Крамера.

**************************************************************************

2. МЕТОД ГАУССА. Составляем расширенную матрицу системы. Для этого к матрице системы добавляем столбец свободных членов.

> restart:

> with(LinearAlgebra):

> A:=<<5,1,-1>|<-3,1,-2>|<1,1,2>|<14,2,2>>;

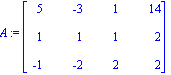
С помощью элементарных преобразований над расширенной матрицей системы под главной диагональю получаем нули.

> Ag:=GaussianElimination(A);

Находим неизвестные с помощью обратного хода:

> z:=Ag[3,4]/Ag[3,3];

> y:=(Ag[2,4]-Ag[2,3]*z)/Ag[2,2];

> x:=(Ag[1,4]-Ag[1,3]*z-Ag[1,2]*y)/Ag[1,1];

2а. ПРОЦЕДУРА МЕТОДА ГАУССА С ПЕЧАТЬЮ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ.

Если не пользоваться пакетом LinearAlgebra, то можно составить процедуру решения системы линейных уравнений методом исключения Гаусса с промежуточной печатью:

> with(linalg):

> gauss_solve_print:=proc(a::matrix,b::vector)

local i,j,k,c,r,x,m;

if rowdim(a)<>vectdim(b) then

error("number of columns of the matrix

must be equal to number of rows of the vector",a,b);

elif coldim(a)<>rowdim(a) then

error("matrix must be square",a);

end if;

m:=rowdim(a);

c:=a;

# Объединение матриц, создание расширенной матрицы:

c:=concat(c,b); print(eval(c));

x:=vector(m);

# Прямой ход

for i from 1 to m do

r:=1/c[i,i];

c:=mulrow(c,i,r);

# i-я строка расширенной матрицы умножается на r

print(eval(c));

if i<>m then

for j from i+1 to m do

r:=-c[j,i];

c:=addrow(c,i,j,r); # прибавление строки

end do;

end if;

end do;

# Обратный ход

x[m]:=c[m,m+1];

for i from m-1 to 1 by -1 do

x[i]:=c[i,m+1]-sum(x[k]*c[i,k],k=(i+1)..m);

end do;

eval(x);

end proc:

> A:=matrix(3,3,[[5,-3,1],[1,1,1],[-1,-2,2]]);

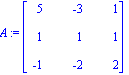
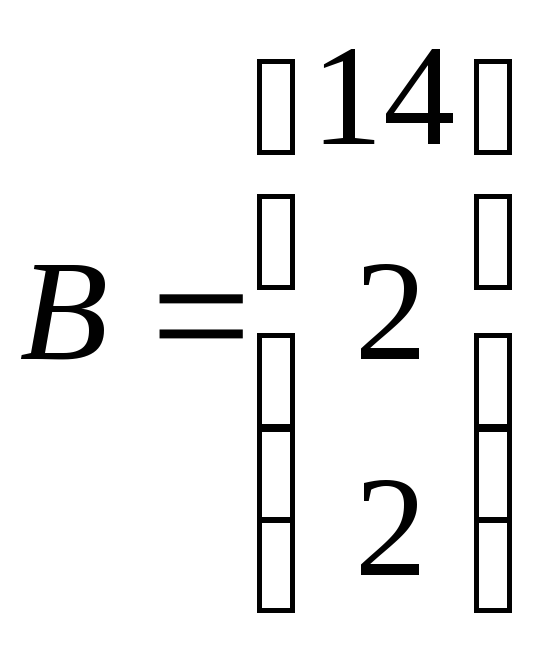
> B:=vector(3,[14,2,2]);

> sol:=gauss_solve_print(A,B);

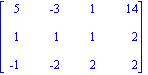
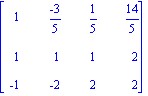
ЗАДАНИЯ.

1. Объяснить работу процедуры.

2. Решить систему своего варианта методом Гаусса с использованием этой процедуры.

******************************************************************************

3. МАТРИЧНЫЙ МЕТОД.

Найдём обратную матрицу.

> Ai:=inverse(A);

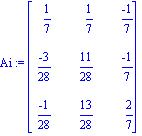
Проверим, что произведение исходной матрицы А на обратную Аi равно единичной матрице.

> multiply(A,Ai);

В обратном порядке (матрицы, вообще говоря, не обладают коммутативностью):

> multiply(Ai,A);

Обратная матрица найдена верно. Найдём столбец неизвестных:

> xyz:=multiply(Ai,B);

Выпишем ответ:

> x:=xyz[1]; y:=xyz[2]; z:=xyz[3];

ЗАДАНИЕ.

1) Найти матрицу, обратную к Аi. Что это за матрица?

2) Проверить правильность расчёта, умножив А на Аi (получить единичную матрицу), затем Аi на А.

3) Решить систему матричным методом.

4) Сделать проверку: перемножить матрицы А и xyz. Какая матрица должна получиться?

******************************************************************************

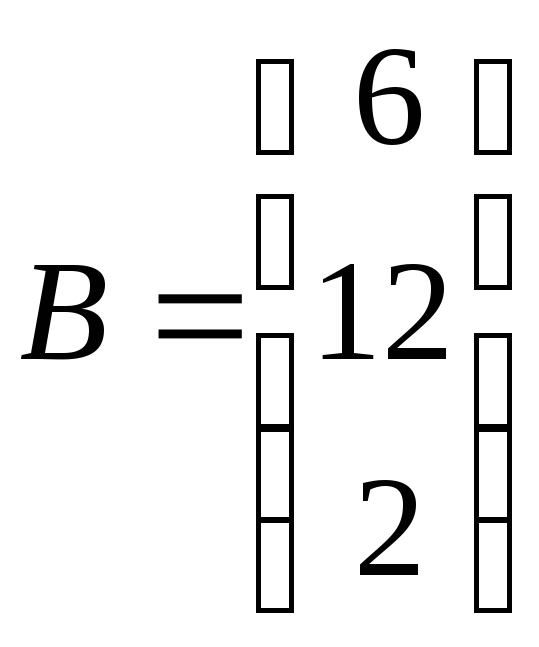
ЗАДАНИЕ. РЕШИТЬ ТРЕМЯ МЕТОДАМИ СИСТЕМУ УРАВНЕНИЙ (по вариантам):

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.

*****************************************************************************