ЛАБ MAPLE ИС / лаб 09-4-ряды Тейлора-задание
.docЛАБОРАТОРНАЯ РАБОТА № 7. РЯДЫ. ЧАСТЬ 4. РЯДЫ ТЕЙЛОРА
Рядом Тейлора функции
![]() в окрестности точки
в окрестности точки
![]() называется степенной ряд
называется степенной ряд
![]() .
Обычно ряд Тейлора представляют в виде
суммы п членов и остаточного члена
в форме Пеано, т.е. бесконечно малой того
же порядка, что первый отброшенный член
ряда:
.
Обычно ряд Тейлора представляют в виде
суммы п членов и остаточного члена
в форме Пеано, т.е. бесконечно малой того
же порядка, что первый отброшенный член
ряда:
![]() .
.
В Maple для разложения в ряд Тейлора предусмотрено несколько процедур, мы рассмотрим процедуру taylor(f,x=x0,n) .Первым параметром ее является раскладываемая в ряд функция. Ее можно задавать в виде выражения, зависящего от х, или в виде переменной, которой заранее это выражение присвоено. Вторым параметром процедуры является равенство, определяющее переменную и точку, в окрестности которой выполняется разложение в ряд. Третьим (необязательным) параметром является порядок остатка ряда.
I. РАЗЛОЖЕНИЕ В РЯД ТЕЙЛОРА. Разложим в ряд Тейлора экспоненту в окрестности нуля (это будет ряд Маклорена), удерживая 9 членов ряда:
> taylor((exp(x)),x=0,10);
![]()
-
Разложите экспоненту в ряд в окрестности единицы и двойки, оставляя различное число членов.
-
Разложите синус в окрестности 0 и .
II. СРАВНЕНИЕ ГРАФИКОВ ФУНКЦИИ И ЕЕ ПРИБЛИЖЕНИЯ С ПОМОЩЬЮ ПОЛИНОМА.
Чтобы отбросить остаток ряда, т.е.
превратить ряд в полином, нужно
воспользоваться процедурой convert(),
преобразующей результат операции
разложения в ряд в многочлен. Зададим
функцию
![]() с помощью переменной f,
разложим ее в ряд и преобразуем в полином:
с помощью переменной f,
разложим ее в ряд и преобразуем в полином:
> f:=1/(1-x);
![]()
> taylor(f,x=0,7);
![]()
> f1:=convert(%,polynom);
![]()
Теперь можно сравнить, насколько отличаются исходная функция и ее приближение рядом Тейлора. Построим на одном чертеже 2 графика, задав цвет, стиль линий и легенду:
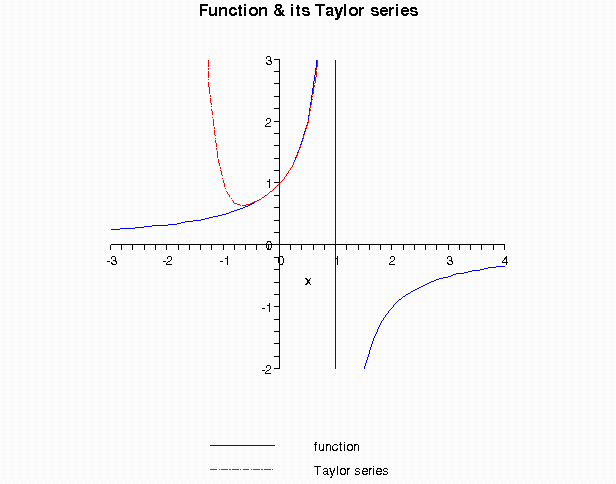
> plot([f,f1],x=-3..4,-2..3,color=[BLUE,RED], linestyle=[SOLID,DASHDOT],title="Function & its Taylor series",titlefont=[HELVETICA,BOLD,13],legend=["function","Taylor series"]);
-
Разложите ту же функцию в окрестности 0, удерживая 20 членов ряда. Постройте график.
-
Проделайте то же в окрестности 2.
-
Разложите
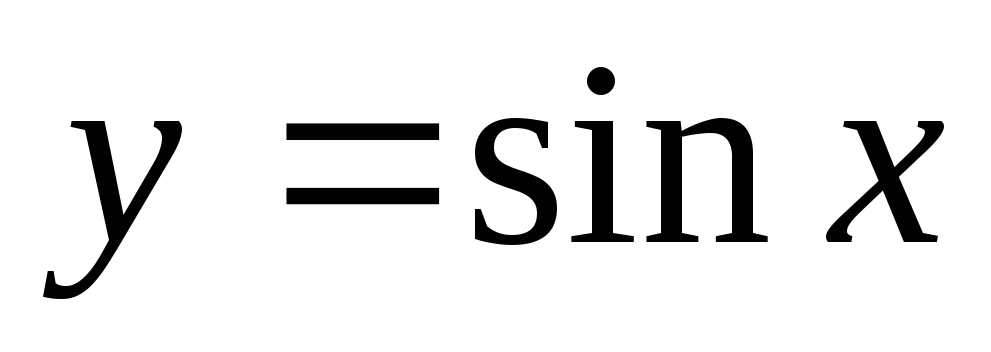 в окрестности 0, удерживая 10 и 40 членов
ряда. Постройте график.
в окрестности 0, удерживая 10 и 40 членов
ряда. Постройте график.
III. ПРОЦЕДУРА.
Составим процедуру, представляющую
разложение функции f
в ряд в окрестности точки
![]() до слагаемых порядка п, преобразуя
такое разложение в полином. Разложим
экспоненту и построим график:
до слагаемых порядка п, преобразуя
такое разложение в полином. Разложим
экспоненту и построим график:
> polly:=(f,x0,n)->convert(taylor(f,x=x0,n),polynom);
![]()
> f:=exp(x);
![]()
> polly(f,0,5);
![]()
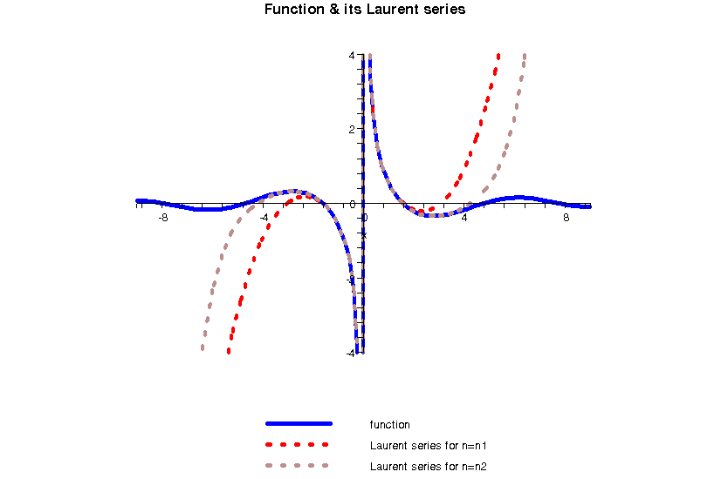
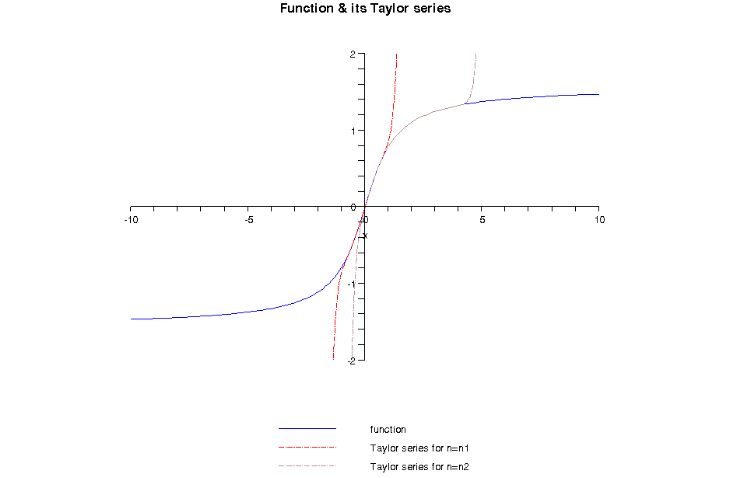
> plot([f,polly(f,0,5),polly(f,0,10)],x=-10..10,-2..2,color=[BLUE,RED,PINK],linestyle=[SOLID,DASHDOT,DOT],numpoints=150,title="Function & its Taylor series",titlefont=[HELVETICA,BOLD,13],legend=["function","Taylor series for n=n1","Taylor series for n=n2"]);

-
Разложите экспоненту в окрестности 1. Постройте график.
-
Разложите функцию
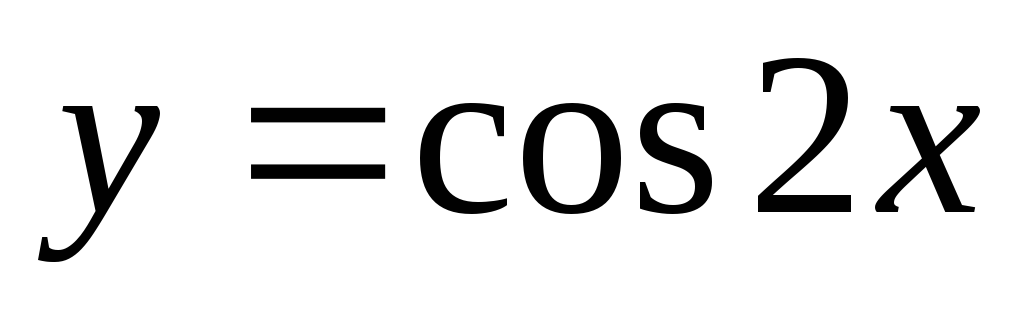 в окрестности /2.
Постройте графики с основной функцией
и полиномами 20-го и 40-го порядков.
в окрестности /2.
Постройте графики с основной функцией
и полиномами 20-го и 40-го порядков. -
Разложите функцию
 в окрестности 0 и 2, удерживая 10 и 20 членов
ряда. Постройте графики.
в окрестности 0 и 2, удерживая 10 и 20 членов
ряда. Постройте графики. -
Разложите в ряд Тейлора функции ln(5x+10), удерживая 5 и 20 членов ряда. Постройте графики.
-
То же проделайте для функции sin(3x-7).
IV ЦИКЛ.
Сделаем цикл рисунков, показывающих фазы приближения графика функции графиками полиномов все больших степеней. Для этого напишем процедуру, которая будет разлагать функцию в ряд Маклорена и отсекать п членов ряда:
> Macloren:=(f,n)->convert(taylor(f,x=0,n),polynom);
1. Разложим в ряд экспоненту
![]() и отбросим все члены ряда, начиная с
10-го:
и отбросим все члены ряда, начиная с
10-го:
> Macloren(ex,10);
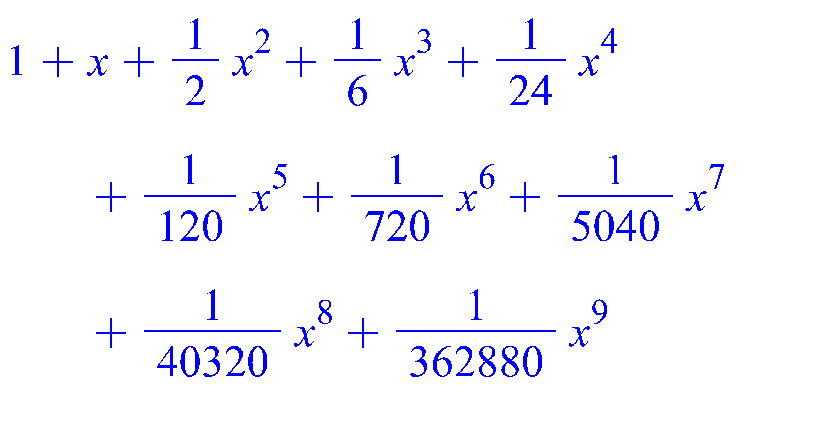
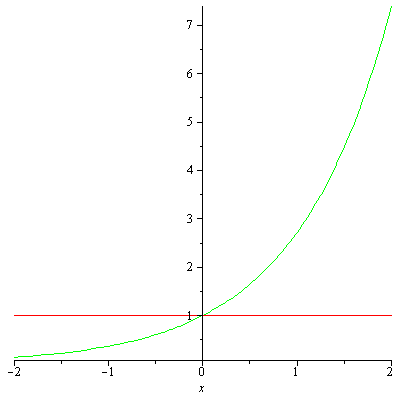
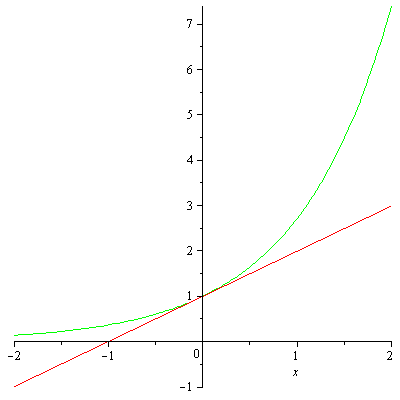
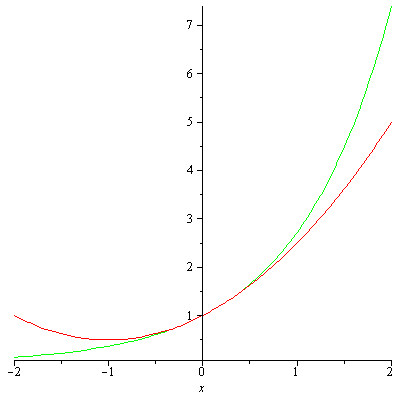
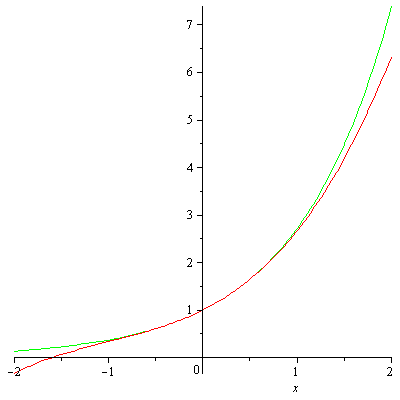
> for i from 1 to 6 do ex1:=Macloren(ex,i); plot([exp(x),ex1],x=-2..2,color=[GREEN,RED]) end do;
>
![]()
![]()
![]()
![]()
![]()
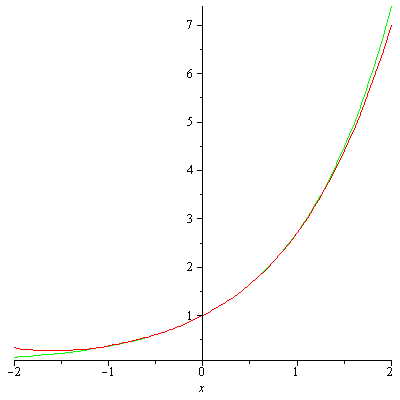
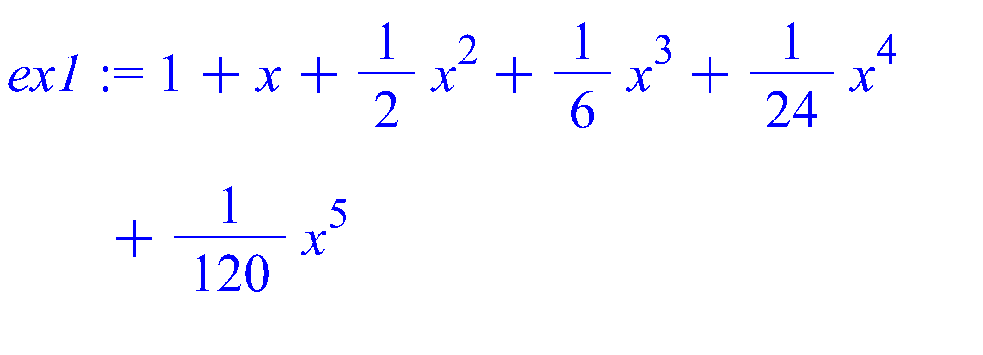
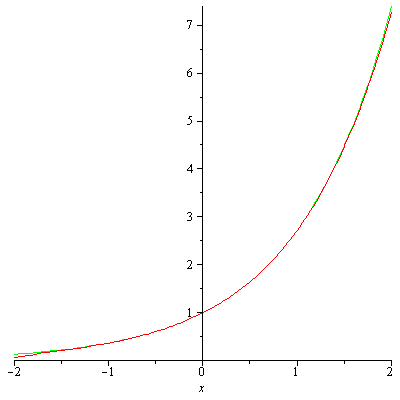
Здесь цикл работает правильно.
2. Разложим в ряд гиперболический синус
![]() и отбросим все члены ряда, начиная с
10-го:
и отбросим все члены ряда, начиная с
10-го:
> sh:=sinh(x);
![]()
> Macloren(sh,10);
![]()
Полином содержит только нечетные степени х. Построим графики, соответствующие последовательному удержанию членов ряда. Чтобы цикл не работал при четных i, введем условный оператор проверки на четность (even – четное число, odd – нечетное).
> for i from 1 to 7 do
if is(i,even) then next fi;
sh1:=Macloren(sh,i); plot([sh,sh1],x=-2..2,linestyle=[SOLID,DASHDOT], color=[RED,GREEN]) end do;
![]()

![]()
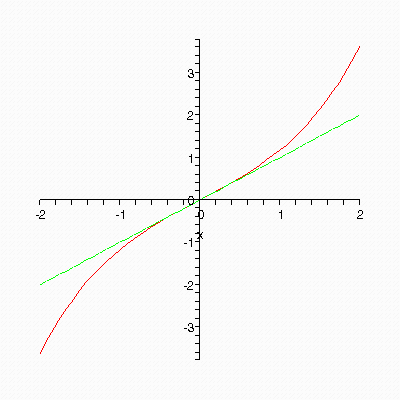
![]()
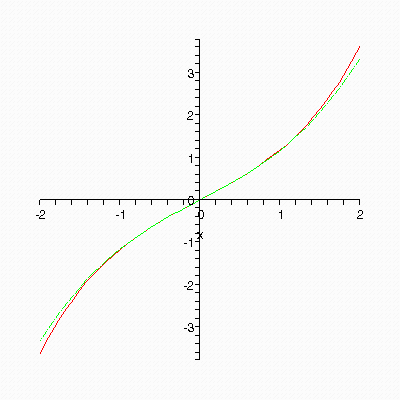
![]()
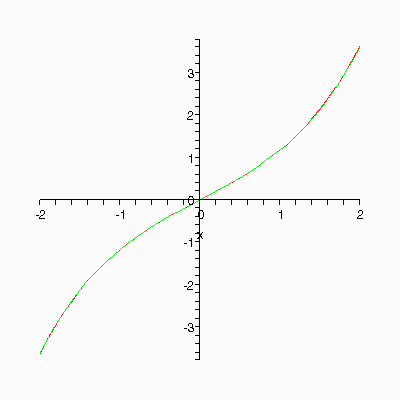
Вопрос: почему печатаются и рисуются члены ряда, начиная с нулевого, а не с первого? Почему заканчиваются не седьмым, а пятым членом ряда? Исправьте цикл.
V. РЯД ЛОРАНА. Попробуйте
разложить в ряд Тейлора функцию
![]() .
Применение процедуры taylor()
не даст результата. Разложите ее в ряд
Лорана, содержащий и члены с отрицательными
степенями
.
Применение процедуры taylor()
не даст результата. Разложите ее в ряд
Лорана, содержащий и члены с отрицательными
степенями
![]() .
Воспользуйтесь процедурой series(),
обращаться к которой нужно так же, как
к taylor().
.
Воспользуйтесь процедурой series(),
обращаться к которой нужно так же, как
к taylor().
Составьте процедуру, аналогичную polly(). Постройте графики.