ЛАБ MAPLE ИС / ЛАБ 8-3 - приложения опред интеграла

7

ЛАБОРАТОРНАЯ РАБОТА № 8-3

ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

Определённые интегралы широко используются в геометрии, физике и механике. С их помощью легко вычисляются длины плоских кривых и площади криволинейных областей, пройденный точкой путь, произведенная работа и многие другие механические и физические величины.

Задача 1. Вычислить длину дуги цепной линии, заданной уравнением y=a ch(x/a), от точки x=0 до текущей координаты x.

Решение. Известно, что дифференциал длины дуги кривой, заданной явным уравнением y=f(x), выражается через производную следующим образом:

Тогда длина дуги кривой, ограниченной точками x=x₀ и x=x₁, определяется через интеграл в виде:

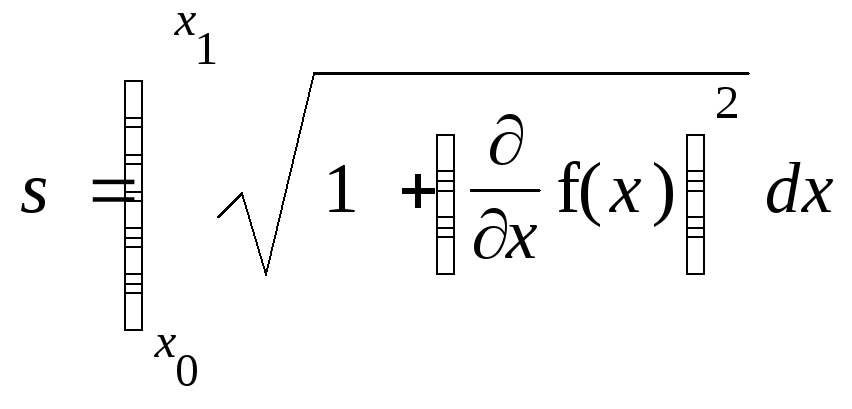
Вычислим для цепной функции производную от длины переменной дуги:

> f:=x->a*cosh(t/a);

> `s'`:=simplify(sqrt(1+diff(f(t),t)^2));

В результате Maple использовал функцию вычисления знака csgn() для выражения cosh(t/a) (мы помним, что гиперболический синус в англоязычной математической литературе обозначается sinh(x), гиперболический косинус cosh(x)). Дело в том, что параметром в команде упрощения simplify() является выражение, содержащее квадратный корень:

> sqrt(1+diff(f(t),t)^2);

Под корнем стоит выражение, которое упрощается до квадрата функции cosh(t/a), а так как результат извлечения квадратного корня из квадрата действительного числа зависит от знака числа, то Maple как раз и использует функцию csgn() для отражения этого факта. Однако мы знаем, что функция гиперболического косинуса всегда положительна, а поэтому можем немного упростить полученное выражение, убрав из него функцию вычисления знака:

> `s'`:=op(2,`s'`);

Теперь, имея выражение для дифференциала дуги цепной линии, можно вычислить и ее длину:

> Int(`s'`,t=0..x)=int(`s'`,t=0..x);

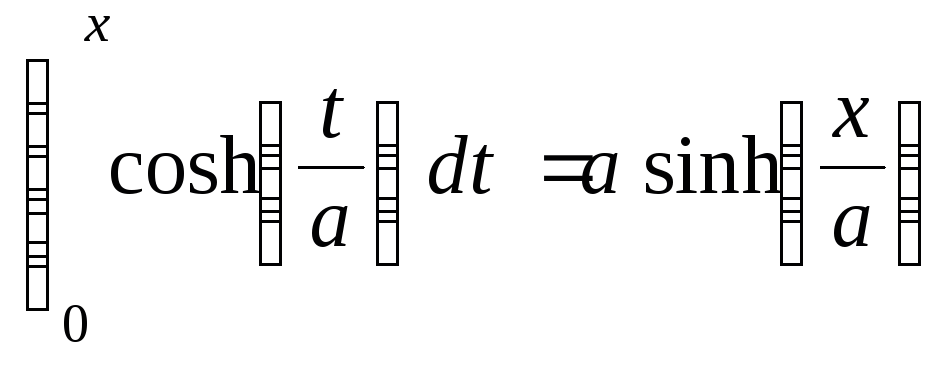
Используя аналогичный подход, можно вычислять длины дуг параметрически заданных кривых. Единственное, что надо помнить, это формулу дифференциала длины дуги параметрически заданной кривой (x=x(t), y=y(t)):

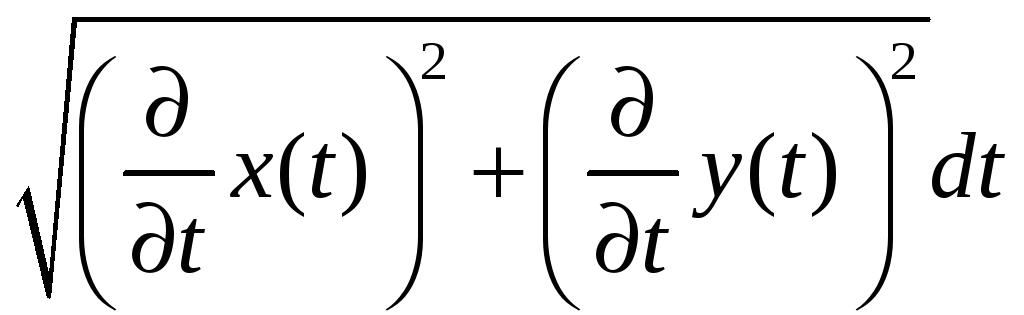
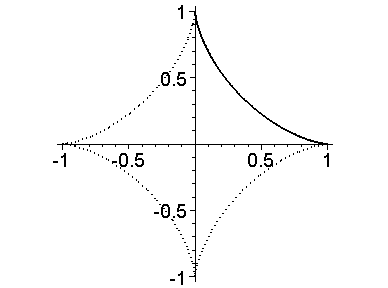
Задача 2. Вычислить длину дуги четверти астроиды x=a cos³ t, y=a sin³ t (0 t/2).

Решение. Начертим сначала график астроиды и выделим дугу, длину которой необходимо вычислить:

> x:=a*cos(t)^3; y:=a*sin(t)^3;

> f:=plot([eval(x,a=1),eval(y,a=1),t=0..2*Pi],color=black,

linestyle=7,thickness=2):

g:=plot([eval(x,a=1),eval(y,a=1),t=0..Pi/2],color=black,

linestyle=1,thickness=2):

with(plots):

display({f,g},scaling=CONSTRAINED);

На рисунке астроида отображается точечной линией, а ее четверть сплошной линией.

Теперь вычислим производную длины дуги астроиды и определённый интеграл от неё на заданном интервале изменения параметра t, величина которого и будет равна длине четверти астроиды:

> `s'`:=simplify(sqrt(diff(x,t)^2+diff(y,t)^2));

> Int(`s'`,t=0..Pi/2)=int(`s'`,t=0..Pi/2);

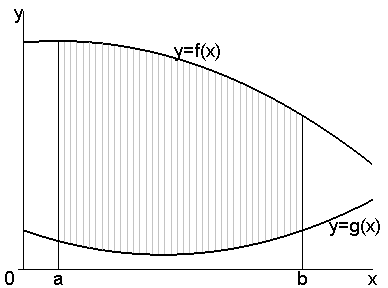
Из определения определённого интеграла нам известно, что если подынтегральная функция f(x) на некотором промежутке [a,b] изменения независимой переменной x положительна, то интеграл равен площади криволинейной трапеции – фигуры, ограниченной сверху кривой y=f(x), слева и справа двумя ординатами x=a и x=b и снизу отрезком [a,b] оси x. Если фигура ограничена снизу не отрезком оси x, а также некоторой кривой y=g(x) (причем эта кривая не обязательно должна быть положительна), то площадь подобной фигуры определяется по формуле:

Рисунок примера 1 иллюстрирует сказанное выше относительно вычисления площади криволинейной трапеции.

Пример 1. Вычисление площади фигуры

> with(plots):

g2:=-0.1*(x-1)^2+15:

g1:=0.1*(x-4)^2+1:

n:=40:

f0:=plot(g1,x=0..10,0..17,color=black,thickness=2):

f1:=plot(g2,x=0..10,color=black,thickness=2):

f2:=seq(plot([[1+7/(n-1)*(i-1),eval(g2,x=1+7/(n-1)*(i-1))],

[1+7/(n-1)*(i-1),eval(g1,x=1+7/(n-1)*(i-1))]],color=gray),i=2..n-1):

f3:=plot([[1,0],[1,eval(g2,x=1)]],color=black):

f4:=plot([[8,0],[8,eval(g2,x=8)]],color=black):

f5:=textplot([1,0,"a"],align=BELOW):

f6:=textplot([8,0,"b"],align=BELOW):

f7:=textplot([0,17,"y"],align=LEFT):

f8:=textplot([10,0,"x"],align=BELOW):

f9:=textplot([5,14,"y=f(x)"],align=ABOVE):

f10:=textplot([9.5,3.5,"y=g(x)"],align=BELOW):

display({seq(f||i,i=0..10)},xtickmarks=[],ytickmarks=[0]);

Замечание

Обратите внимание, что задание пустого списка засечек горизонтальной оси в опции xtickmarks, а также одного значения 0 для засечек по вертикальной оси приводит к вычерчиванию осей координат вообще без засечек с единственной маркированной точкой – началом координат.

Задача 3. Найти площадь фигуры, ограниченной осями координат и параболой

, (a > 0).

Р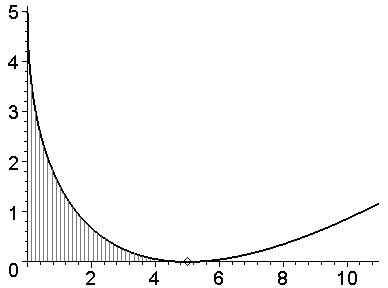ешение. Прежде всего, выразим уравнение параболы в явном виде и начертим ее график. Из задания параболы ясно, что независимая переменная x должна быть неотрицательной:

> f:=sqrt(x)+sqrt(y)=sqrt(a);

> f:=rhs(isolate(f,y));

> with(plots):

a1:=a:

n:=40:

f0:=plot(eval(f,a=5),x=0..11,0..7,color=black,thickness=2):

f1:=seq(plot([[eval(a1,a=5)/(n-1)*(i-1),0],

[eval(a1,a=5)/(n-1)*(i-1),

eval(f,[x=eval(a1,a=5)/(n-1)*(i-1),a=5])]]),i=1..n):

f2:=plot([[eval(a1,a=5),0]],style=POINT, symbol=DIAMOND, symbolsize=16,

color=black):

f3:=textplot([0.1,5,"a"],align=RIGHT):

f4:=textplot([5,0,"a"],align=BELOW):

f5:=textplot([0,7,"y"],align=LEFT):

f6:=textplot([11,0,"x"],align=BELOW):

display({f0,f1,f2,f3,f4,f5,f6},xtickmarks=[],ytickmarks=[0]);

Точку пересечения графика параболы с осью абсцисс найдем из решения уравнения:

> p:=solve(f,x);

Теперь можно вычислить искомую площадь как интеграл:

> Int(f,x=0..p)=int(f,x=0..p);

Задача 4. Определить площадь фигуры, заключенной между двумя параболами y²=2px и x²=2py.

Решение. Как и в предыдущей задаче, сначала мы построим графики парабол, чтобы выяснить их взаимное расположение:

> ff:=y^2=2*p*x;

> f:=sqrt(2*p*x);

> g:=x^2/2/p;

> with(plots):

n:=20:

f0:=implicitplot(eval(ff,p=1),x=-3..3,y=-3..3,color=black,thickness=2):

f1:=plot(eval(g,p=1),x=-3..3,color=black,thickness=2):

f2:=seq(plot([[2./(n-1)*(i-1),eval(f,[p=1,x=2/(n-1)*(i-1)])],

[2/(n-1)*(i-1),eval(g,[p=1,x=2/(n-1)*(i-1)])]],color=gray),i=1..n):

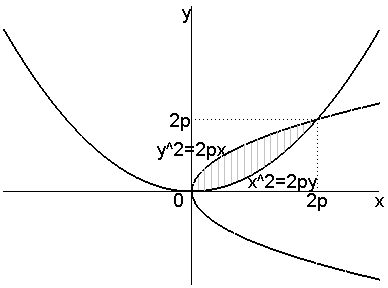f3:=plot([[2,0],[2,2]],color=black,linestyle=7):

f4:=plot([[0,2],[2,2]],color=black,linestyle=7):

f5:=textplot([2,0,"2p"],align=BELOW):

f6:=textplot([0,2,"2p"],align=LEFT):

f7:=textplot([0,5,"y"],align=LEFT):

f8:=textplot([3,0,"x"],align=BELOW):

f9:=textplot([0,1,"y^2=2px"],align=ABOVE):

f10:=textplot([2,0.1,"x^2=2py"],align={ABOVE,LEFT}):

display({seq(f||i,i=0..10)},xtickmarks=[],ytickmarks=[0]);

Из рисунка видно, что две параболы пересекаются в двух точках, координаты которых можно определить из решения системы уравнений:

> eq1:=y=f;eq2:=y=g;

> c:=solve({eq1,eq2},{x,y});

Из полученного множества решений нас, естественно, интересуют только действительные {x=0, y=0} и {x=2p, y=2p}, из которых определяется интервал интегрирования для определёния площади фигуры, образованной пересечением конгруэнтных парабол, – [0, 2p]. Определённый интеграл от разности функций f и g по этому промежутку и будет равен площади искомой фигуры:

> S:=int(f-g,x=0..2*p);

> subs(sqrt(p^2)=p,S);

Если параметр p > 0, то можно упростить выражение для площади, заменив в нем на p.

Кроме вычисления длин дуг кривых и площадей определённый интеграл применяется при вычислении объемов тел вращения, образуемых вращением криволинейной трапеции, ограниченной сверху неотрицательной функцией y=f(x), слева и справа прямыми x=a и x=b (a  b), а снизу отрезком [a, b] оси x, вокруг этой оси. В этом случае объем полученного тела можно вычислить по формуле

.

Если фигура ограничена и сверху и снизу кривыми y=f(x) и y=g(x), то, очевидно,

.

Задача 4. Вычислить объем эллипсоидов вращения, образованных вращением эллипса вокруг оси x и оси y.

Решение. Нарисуем на плоскости xy заданный в задаче эллипс:

> with(plots):

f0:=implicitplot(x^2/2^2+y^2/4^2=1,x=-2..2,y=-4..4,

color=black,thickness=2,scaling=CONSTRAINED):

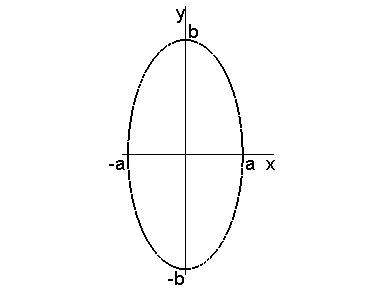f1:=textplot([2.1,0,"a"],align={RIGHT,BELOW}):

f2:=textplot([-2.1,0,"-a"],align={LEFT,BELOW}):

f3:=textplot([0,5,"y"],align=LEFT):

f4:=textplot([3,0,"x"],align=BELOW):

f5:=textplot([0.1,4.1,"b"],align={ABOVE,RIGHT}):

f6:=textplot([0,-4,"-b"],align={BELOW,LEFT}):

display({seq(f||i,i=0..6)},xtickmarks=[],ytickmarks=[]);

Для вычисления объема эллипсоида вращения, образованного вращением вокруг оси x, следует найти квадрат координаты y, а потом вычислить в соответствии с приведённой выше формулой определённый интеграл на промежутке [-a, a]:

> ellips:=x^2/a^2+y^2/b^2=1;

> isolate(ellips,y^2);

> f:=rhs(%);

> V[x]=Pi*Int(f,x=-a..a);

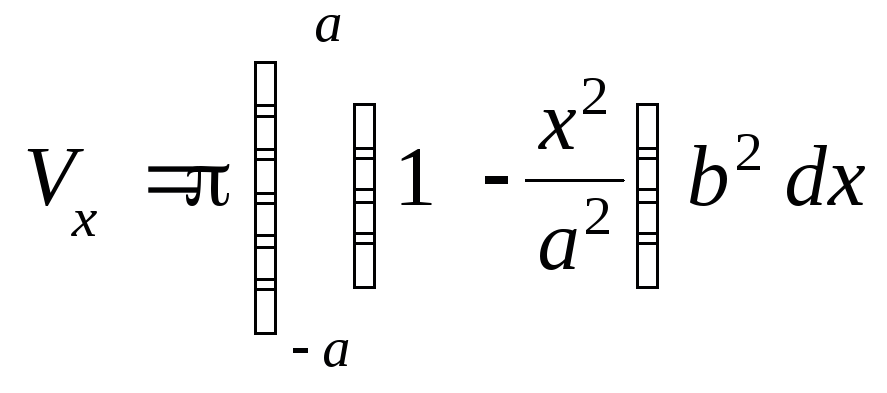
> V[x]=Pi*int(f,x=-a..a);

При вращении эллипса вокруг оси y нам необходимо вычислить определённый интеграл от квадрата координаты x на промежутке [-b, b]:

> isolate(ellips,x^2);

> f:=rhs(%);

> V[y]=Pi*Int(f,y=-b..b);

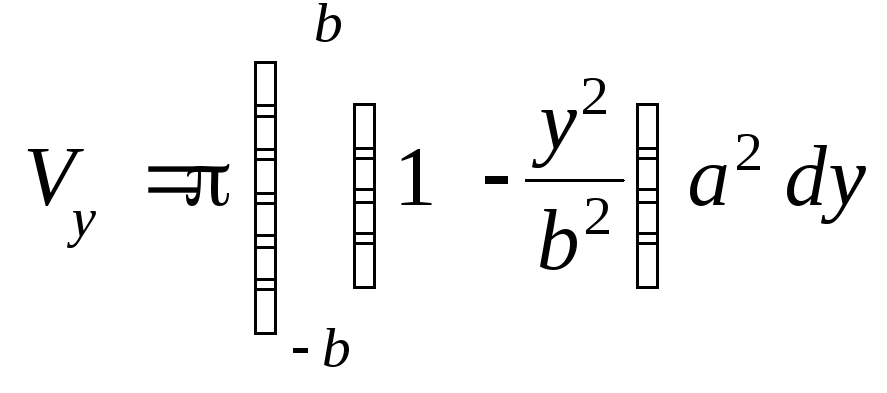
> V[y]=Pi*int(f,y=-b..b);

Задание. Назначить переменным а и b числовые значения, вычислить объёмы эллипсоидов вращения и сравнить их между собой.

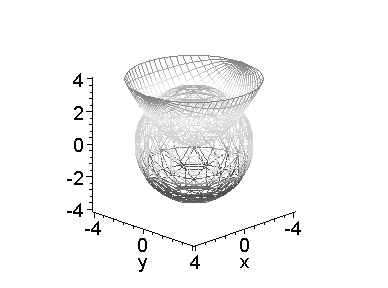
Задача 5. Найти объём общей части параболоида вращения 2az=x²+y² и сферы x²+y²+z²=3a².

Решение. Оба тела являются телами вращения относительно оси z, а поэтому и общая их часть также будет телом вращения относительно этой же оси:

> g:=plot3d((x^2+y^2)/2/2,x=-4..4,y=-sqrt(16-x^2)..sqrt(16-x^2)):

g1:=implicitplot3d(x^2+y^2+z^2=12,x=-4..4,y=-4..4,z=-4..4):

display({g,g1},scaling=CONSTRAINED,axes=FRAME,

shading=ZHUE,style=WIREFRAME,orientation=[45,70]);

Замечание. Для иллюстрации пересечения параболоида вращения и сферы мы задали значение параметра a равным 2.

Для вычисления объема тела, получаемого пересечением параболоида вращения и сферы, необходимо определить уравнение кривой, вращение которой образует их общую часть. Для этого следует построить сечения заданных тел плоскостью, проходящей через ось z, например, xz:

> p:=2*a*z=x^2+y^2;

> s:=x^2+y^2+z^2=3*a^2;

> p[z]:=subs(y=0,p);

> s[z]:=subs(y=0,s);

> f0:=implicitplot({eval(p[z],a=2),eval(s[z],a=2)},x=-4..4,z=0..12,

color=black,thickness=2,scaling=CONSTRAINED):

f1:=plot([[0,2],[sqrt(8),2]],color=black):

f2:=textplot([0,2,"a"],align={LEFT}):

f3:=textplot([0,sqrt(12)+0.2,"sqrt(3)*a"],align={LEFT,ABOVE}):

f4:=textplot([0,5,"z"],align=LEFT):

f5:=textplot([5,0,"x"],align=BELOW):

f6:=plot([[sqrt(8),0],[sqrt(8),2]],color=black):

f7:=textplot([sqrt(8),-0.2,"sqrt(2)*a"],align=BELOW):

display({seq(f||i,i=0..7)},xtickmarks=[],ytickmarks=[]);

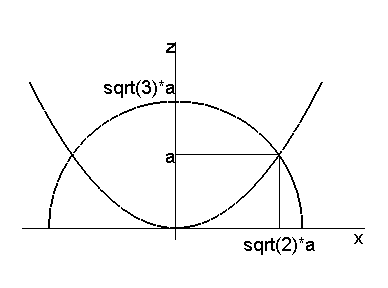
Точки пересечения сечений заданных в задаче тел вращения можно вычислить следующими командами:

> subs(x^2=lhs(p[z]),s[z]);

> solve(%,z);

> z[1]:=%[1];

> x[1]:=simplify(subs(z=z[1],sqrt(lhs(p[z]))),symbolic);

Так как параболоид вращения задан только при z  0, то из двух значений z выбирается первое, которое больше нуля.

Теперь ясно, что сечение тела вращения, являющегося пересечением параболоида и сферы, представляется параболой 2az=x², пока z принадлежит промежутку [0,a], и дугой окружности x²+z²=3a², когда z изменяется в интервале [a, ]. Поэтому объём тела, полученного вращением составной кривой вокруг оси z, представляется суммой двух интегралов:

> V=Pi*Int(lhs(p[z]),z=0..a)+

Pi*Int(rhs(isolate(s[z],x^2)),z=a..sqrt(3)*a);

> V=simplify(Pi*int(lhs(p[z]),z=0..a)+

Pi*int(rhs(isolate(s[z],x^2)),z=a..sqrt(3)*a));