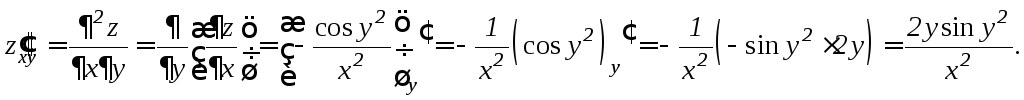10. Функции нескольких переменных

10.1. Понятие функции нескольких переменных, предел и непрерывность функции нескольких переменных

Если каждой точке MDEⁿ по определенному правилу ставится в соответствие одно и только одно число uR, то говорят, что на множестве D задана функция u=f(M), или u=f(x₁,…,x_n). При этом множество D называется областью определения функции.

Область определения функции двух переменных можно изобразить на плоскости.

Пример 1. Изобразить на плоскости область определения следующей функции: .

Р

Рис. 10.1

ешение. Поскольку логарифмическая функция определена для положительных значений ее аргумента, то . Изобразим линию, которая является параболой (см. рис. 10.1). Так как точка (0;0) удовлетворяет неравенству, то заштриховываем ту область, в которой точка находится. Отметим, что границу мы изобразили пунктирной линией, поскольку она не входит в область определения функции.

Линией уровня функции z=f(x,y) называется множество точек плоскости xOy, в которых функция принимает одно и то же значение: f(x,y)=C.

П

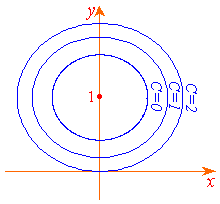Рис. 10.2

ример 2. Построить линии уровня функции .

Решение. Линии уровня u=C – это кривая на плоскости xOy, задаваемая уравнением , или. Это уравнение окружности с центром в точке(0;1) и радиусом (см. рис. 10.2). Таким образом, линии уровня данной функции– это концентрические окружности, радиус которых увеличивается с ростомC>–1, причем расстояние между линиями с одинаковым шагом уровня уменьшается по мере удаления от центра. Таким образом, график исходной функции представляет собой коническую поверхность, вершина которой находится в точке (0;1;–1).

Рассмотрим функцию u=f(M), определенную на множестве DEⁿ, и точку PEⁿ, быть может, и не принадлежавшую множеству D, но обладающую тем свойством, что в любой окрестности этой точки содержится хотя бы одна точка множества D, отличная от P (другими словами, точка P является предельной точкой множества D).

Число a называется пределом функции u=f(M) в точке P (или при MP), если для любого 0 можно указать такое число =()>0 , что для всех точек M, удовлетворяющих условию 0<(M,P)< , выполняется неравенство |f(M)–a|< , записывают

, или .

Здесь (M,P) – расстояние между точкамиM иP : если M(x₁,…,x_n),Pа₁,…,а_nто(M,P)=.

Понятие непрерывности функции нескольких переменных вводится точно также как и для функции одной переменной.

Функция u=f(M) называется непрерывной в точке P, если предел в этой точке существует и равен значению функции в этой точке, т.е.

, или .

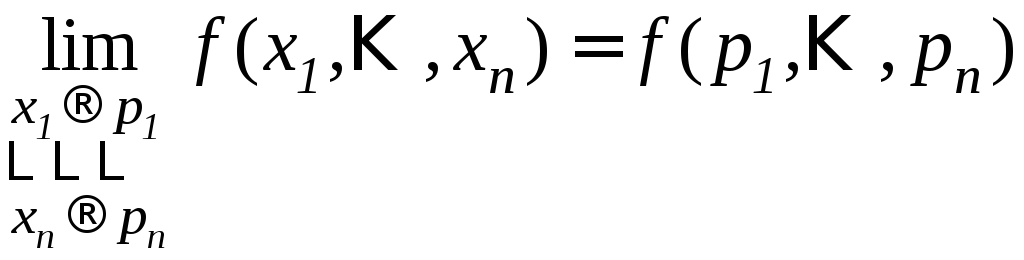10.2. Частные производные

Пусть функция u=f(x₁,x₂,…x_n) определена в некоторой окрестности точки M , включая саму эту точку. Придадим аргументу x_k приращение x_k , тогда функция тоже получит приращение

.

Частной производной от функции u=f(x₁,x₂,…x_n) по независимой переменной x_k называется предел (если он существует и конечен):

.

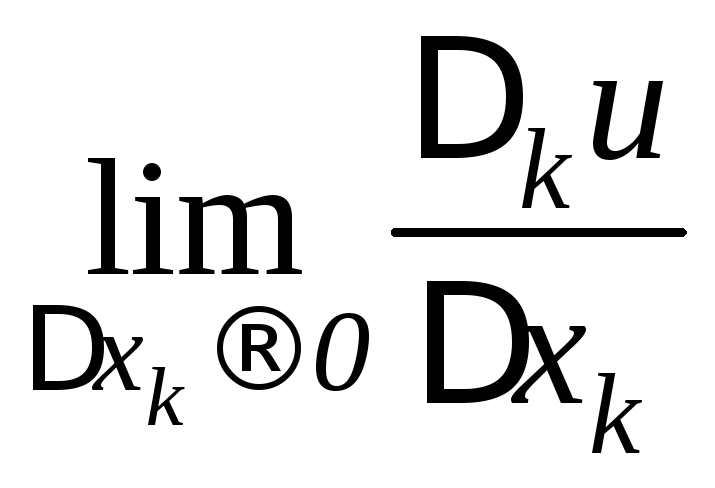Обозначают или. Таким образом, по определению:

.

Отметим, что частная производная по независимой переменной x_k вычисляется при условии, что все другие переменные постоянны. Для частных производных справедливы обычные правила и формулы дифференцирования.

Пример 3. Найти все частные производные функции .

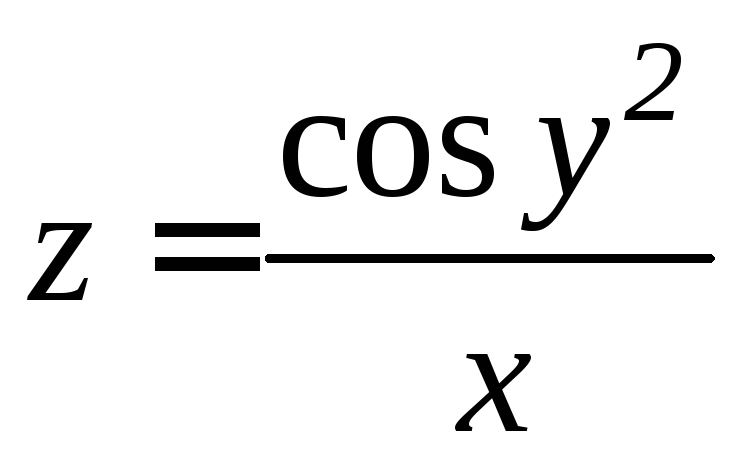Решение. Считая y постоянной, получим:

.

Считая x постоянной, получим:

.

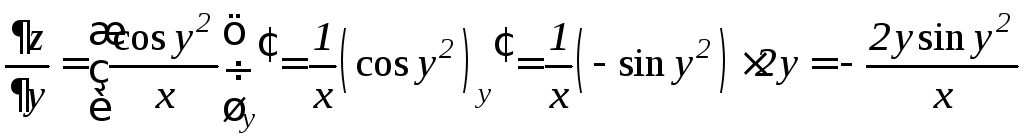Частными производными 2-го порядка функции u=f(x₁,x₂,…x_n) называются частные производные от ее частных производных первого порядка. Производные 2-го порядка обозначаются следующим образом:

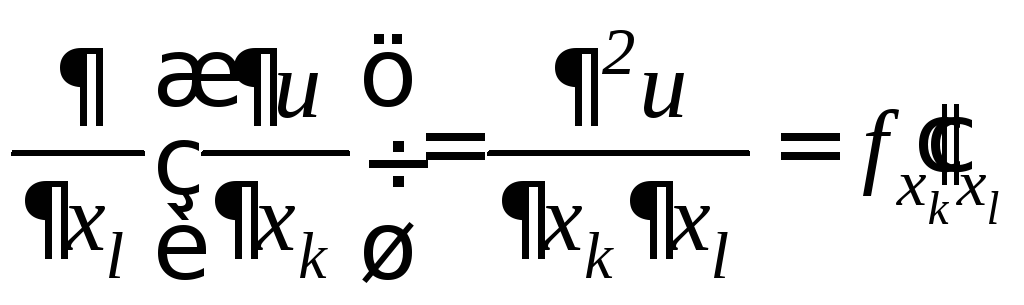, и т.д.

Аналогично определяются производные порядка выше второго.

Отметим, что результат многократного дифференцирования по различным переменным не зависит от очередности дифференцирования, если получающиеся при этом частные производные непрерывны. Если дифференцирование производится по различным переменным, то полученные частные производные называются смешанными.

Пример 4. Найти все частные производные 2-го порядка функции .

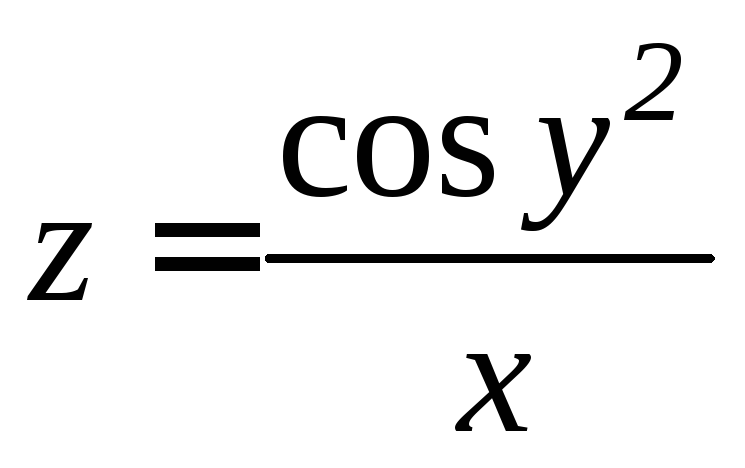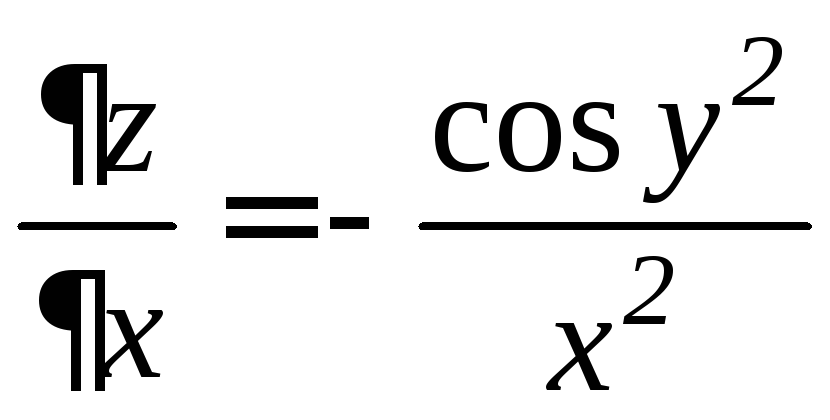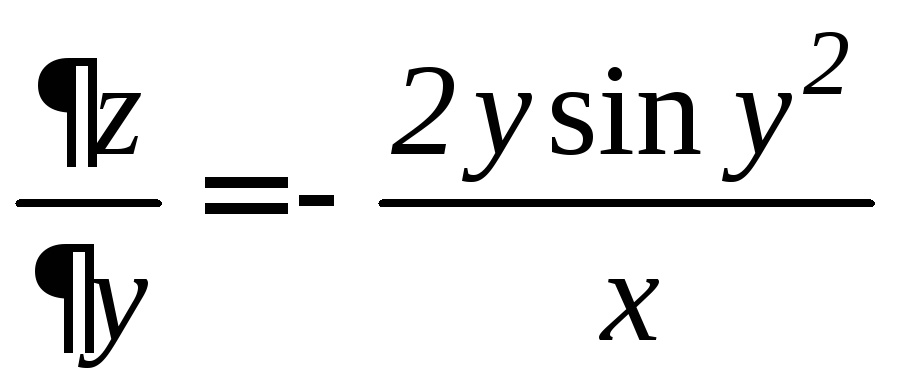Решение. В примере 3 были найдены частные производные 1-го порядка этой функции: и. Найдем частные производные от этих производных, т. е. частные производные 2-го порядка.

Найдем частную производную второго порядка по переменной x :

Найдем частную производную второго порядка по переменной y :

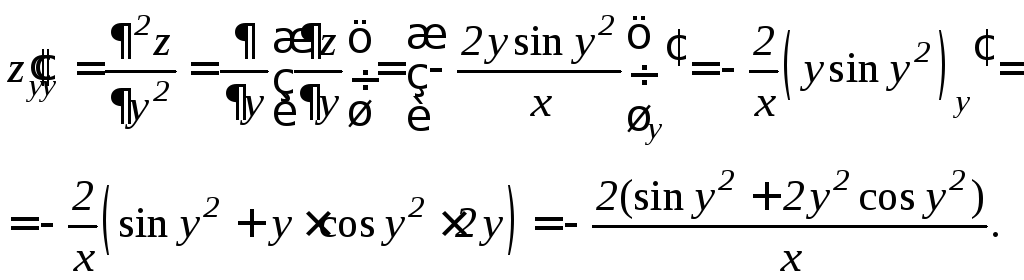
Найдем смешанную частную производную второго порядка: