9. Определенный интеграл и его приложения

9.1. Понятие определенного интеграла

Пусть функция f(x) определена на отрезке [a,b]. Этот отрезок разделим на n произвольных, необязательно равных, частей:

a=x₀ < x₁ < ... < x_n=b.

В этом случае говорят, что произведено разбиение отрезка [a,b]. На каждом участке разбиения [x_i–1, x_i] возьмем произвольную точку _i и вычислим значение функции f(x) в этих точках. Если умножить полученные значения функции f(_i) на длину соответствующего участка x_i = x_i–x_i–1 и просуммировать , то получим

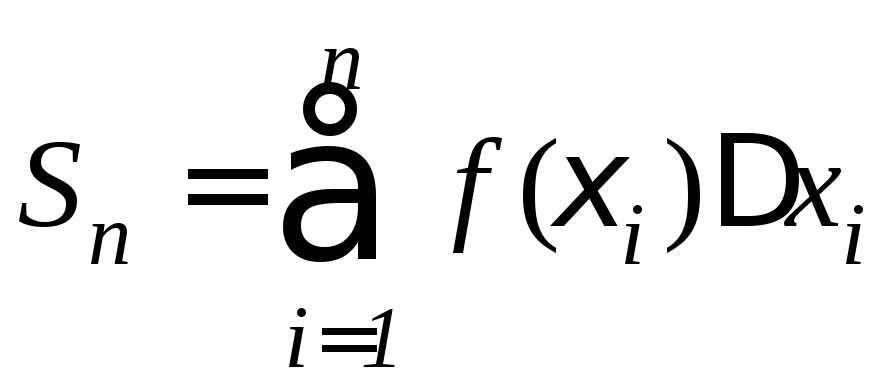, (9.1)

которая называется интегральной суммой функции f(x) на отрезке [a,b].

Обозначим через x =max x_i.

Если предел последовательности интегральных сумм

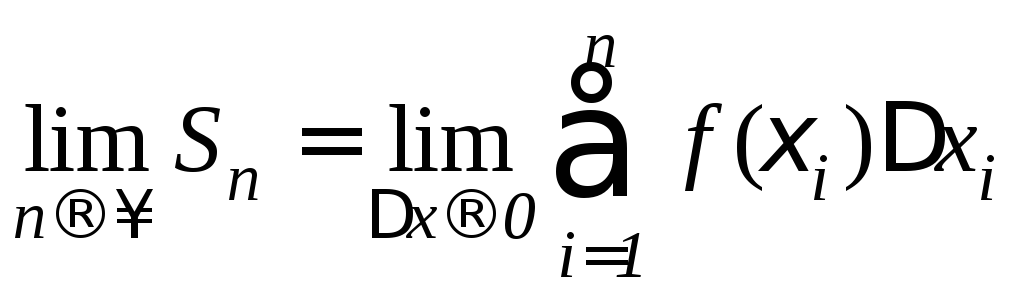. (9.2)

существует, т.е. конечен и не зависит от способа разбиения отрезка [a,b] и от выбора точек _i на соответствующих участках, то этот предел называется

Определенным интегралом функции f(x) на отрезке [a,b] и обозначают

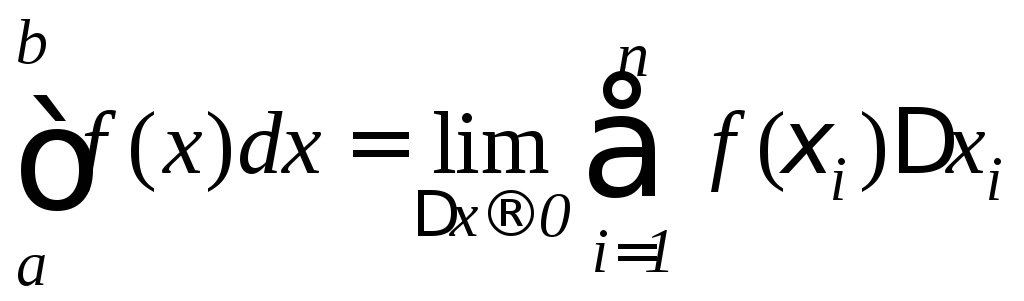. (9.3)

Здесь число a называется нижним пределом, число b называется верхним пределом интеграла.

Функция f(x) называетсяинтегрируемойна отрезке [a,b], если для этой функции на указанном отрезке существует предел интегральных сумм, т.е. определенный интеграл.Необходимое условие интегрируемости: если функцияf(x)интегрируема на отрезке [a,b], то она ограничена на этом отрезке.Достаточное условие интегрируемости: если функцияf(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.

9.2. Свойства определенного интеграла

1. .

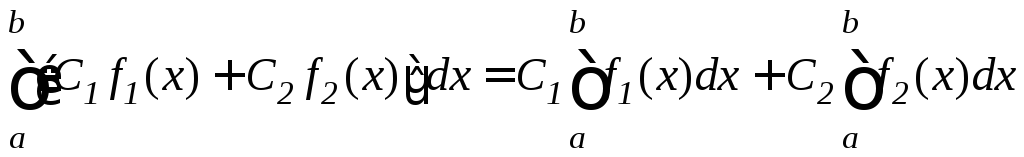2. .

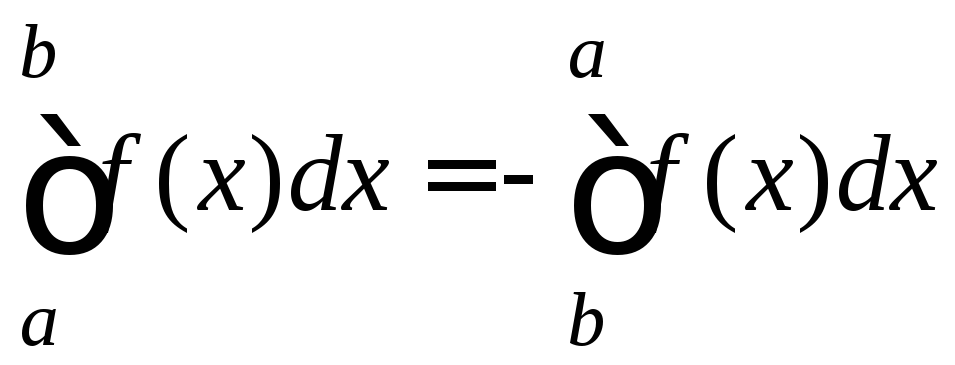3. .

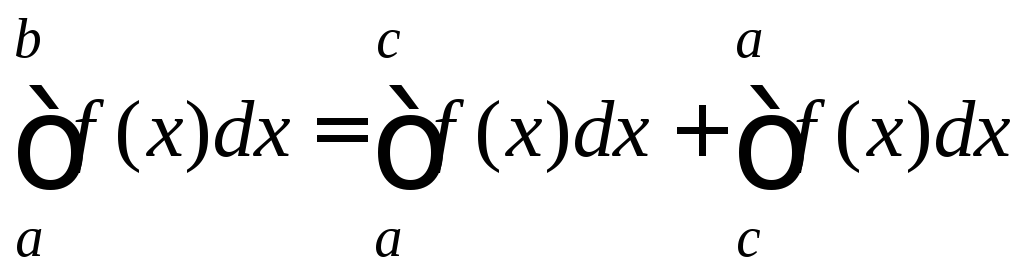4. Если функция f(x) – четная, то ,

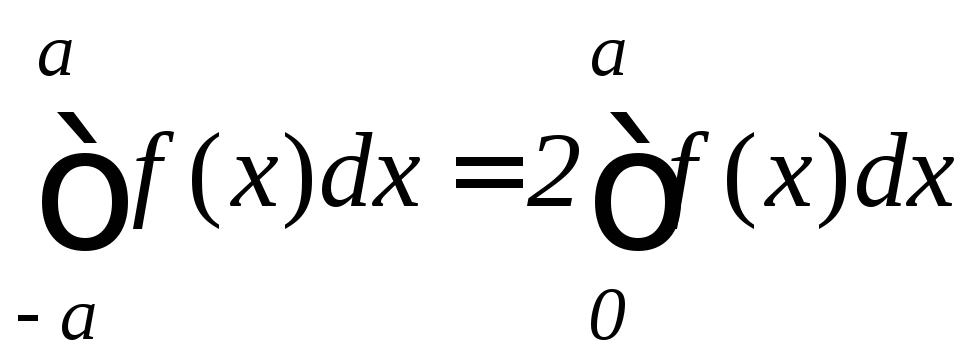если функция f(x) – нечетная, то .

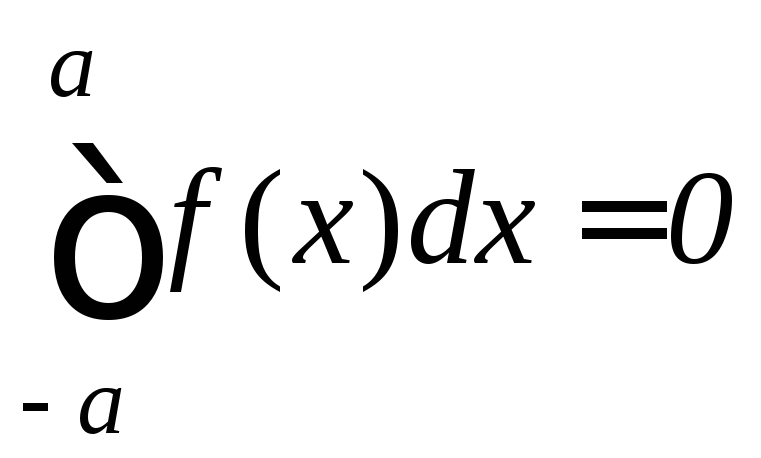9.3. Формула Ньютона-Лейбница

Теорема (формула Ньютона-Лейбница). Если функция f(x) непрерывна на отрезке [a,b] и F(x) – какая-либо ее первообразная на этом отрезке, то имеет место следующая формула:

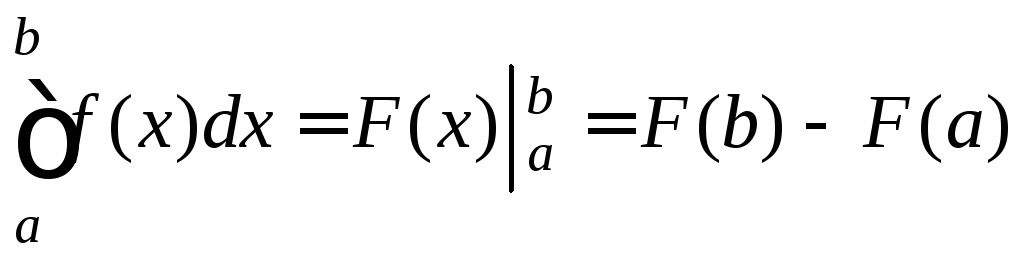. (9.4)

Пример 1. Вычислить интегралы

а) 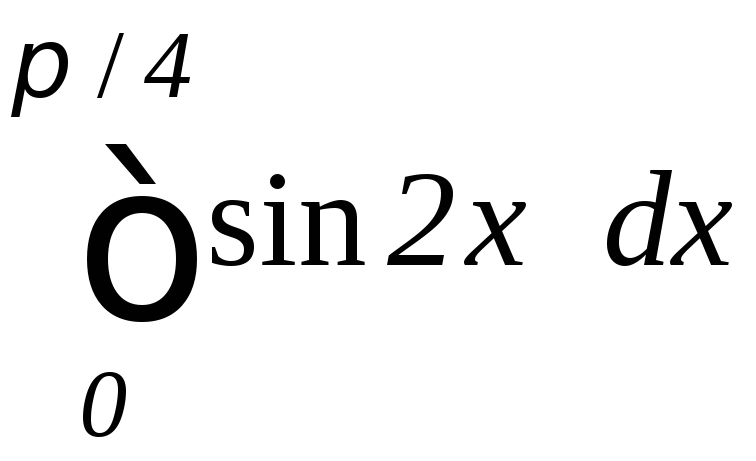, б).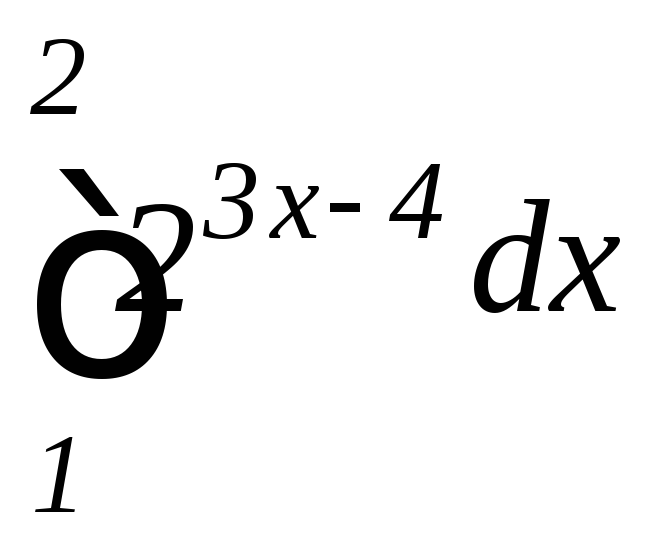

Решение.

а) ,

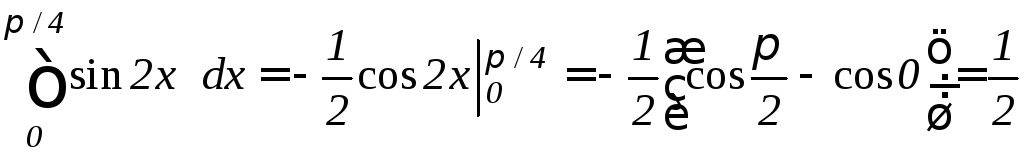б) .

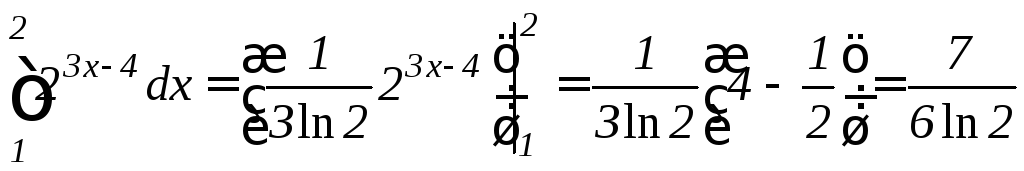9.4. Метод замены переменной в определенных интегралах

Теорема. Если функция f(x) непрерывна на отрезке [a,b], а функция x=(t) дифференцируема на отрезке [t₁,t₂], где a=(t₁) и b=(t₂), то имеет место формула:

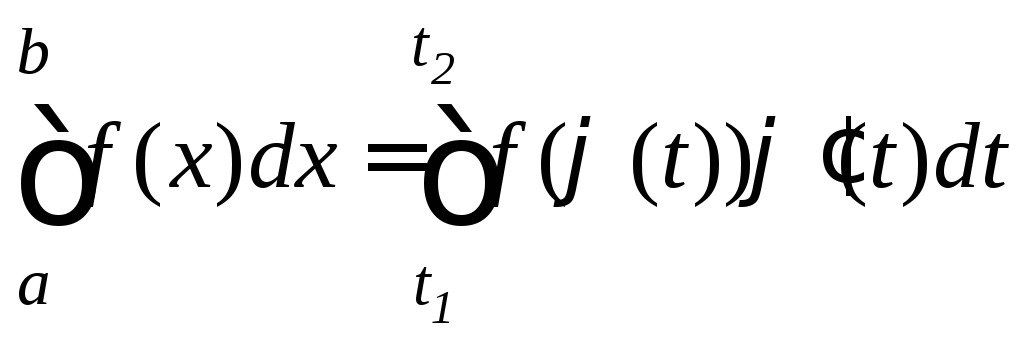. (9.5)

Пример 2. Вычислить интегралы

а) 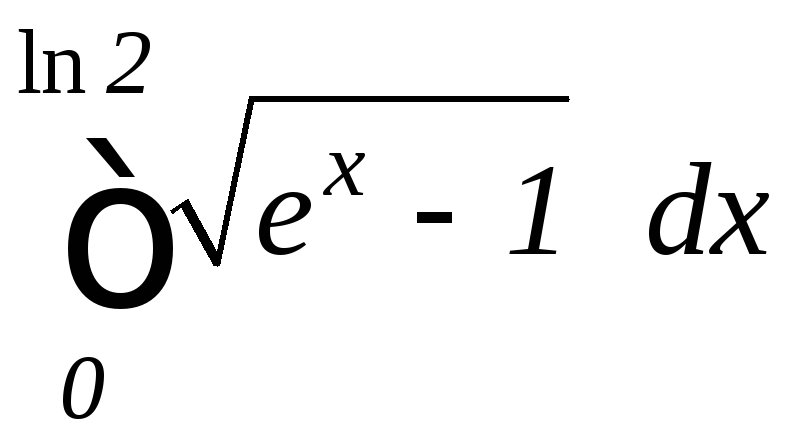, б).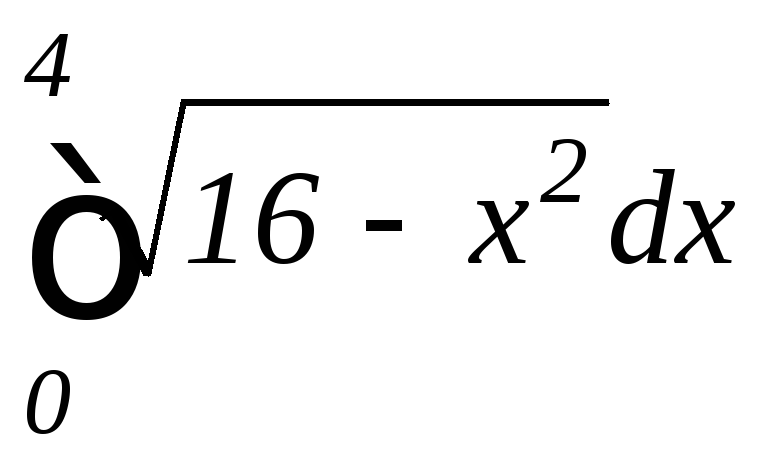

Решение. а) Сделаем замену . Тогдаиdx = 2tdt/(1+t²). Поскольку при x=0 t=0 и при x=ln2 t=1, то получим

.

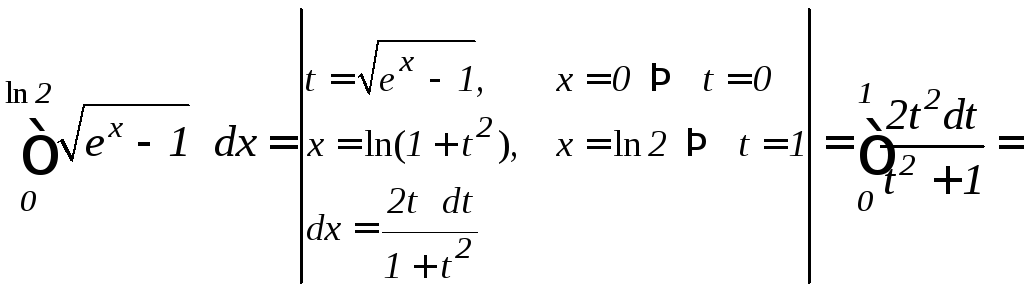
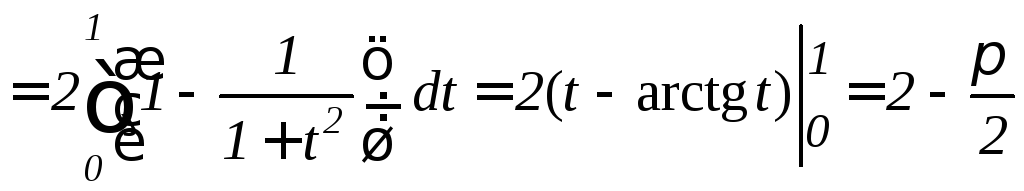б) Сделаем тригонометрическую подстановку x=4sint. Тогда

.

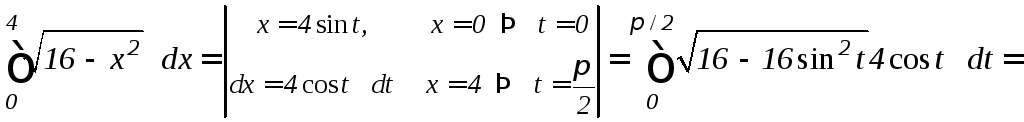
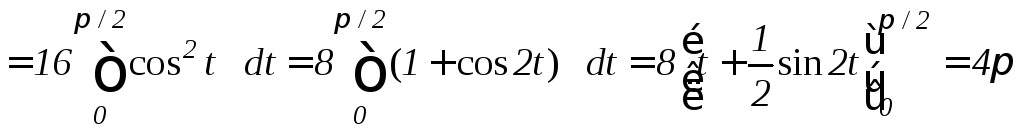Заметим, что при использовании метода замены переменной необходимо проверять выполнение всех перечисленных в теореме условий. Если эти условия нарушаются, то может быть получен неверный результат.

9.5. Метод интегрирования по частям в определенных интегралах

Теорема. Если функции u=u(x) и v=v(x) непрерывны вместе со своими производными на отрезке [a,b], то имеет место формула:

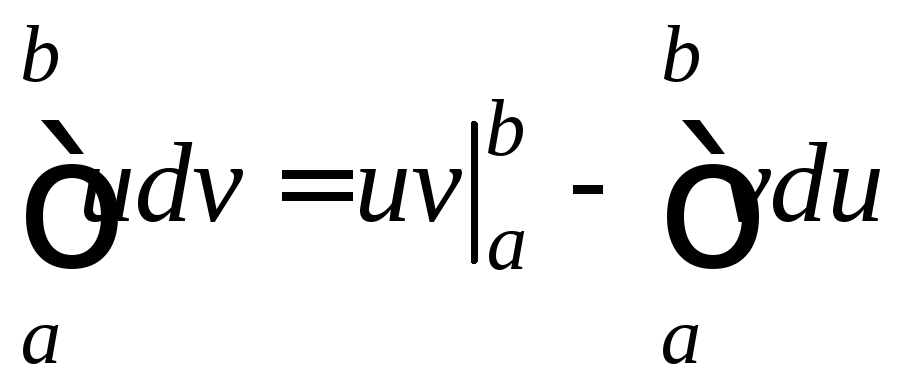. (9.6)

Пример 3. Вычислить интегралы

а) 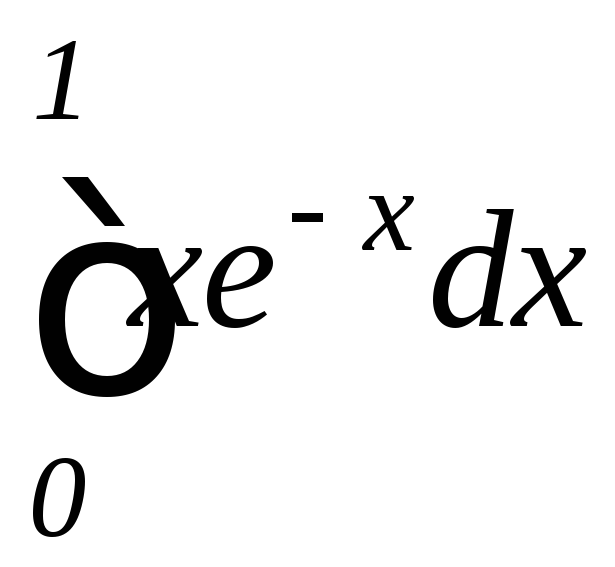, б).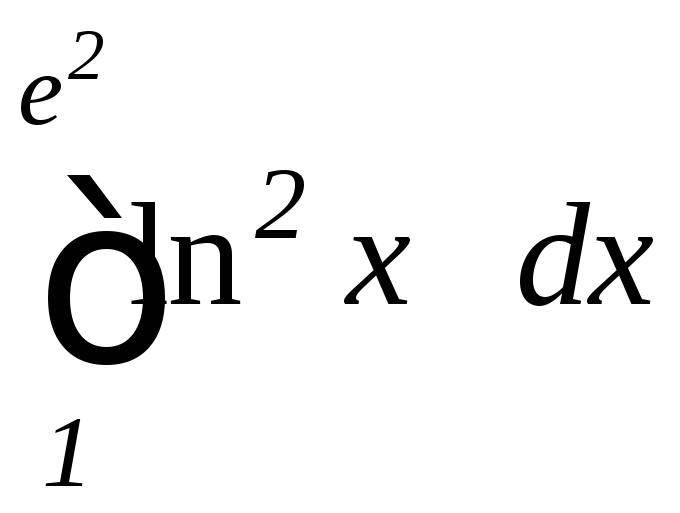

Решение. а) Воспользуемся формулой (9.6) интегрирования по частям, для этого положим u=x, dv=e^–xdx, откуда du=dx, v=–e^–x. Тогда

.

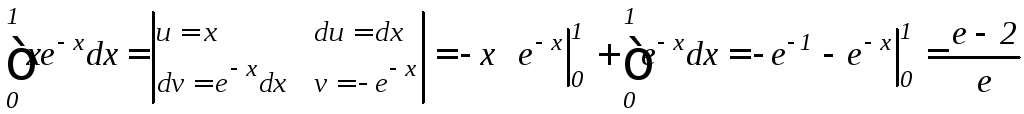б) Применяя формулу интегрирования по частям, получим

.
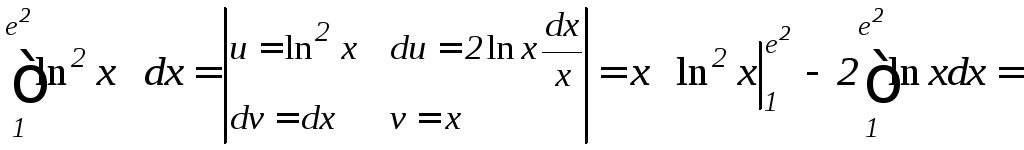
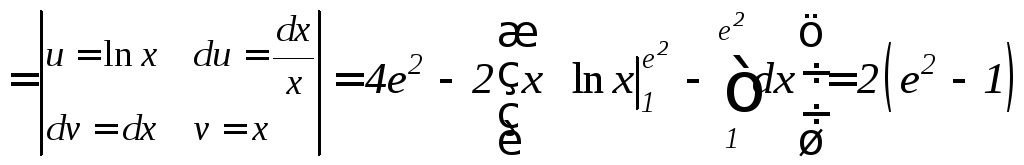