1. Определители и матрицы. Системы линейных уравнений

1.1. Матрицы и определители

Таблицы вида

,

где а_ij, i=1, …. , m, j=1, …. , n - числа, называются матрицами. При m=n - матрица квадратная, при m≠n – прямоугольная.

Определителем 2-ого порядка, соответствующим матрице

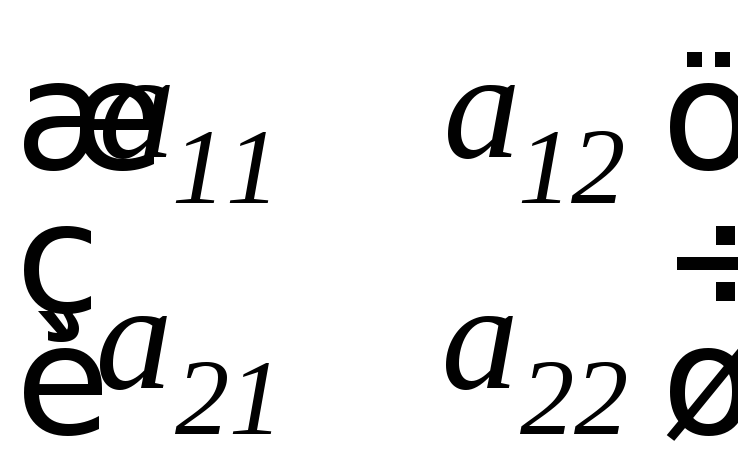А =, называется число |А| = .

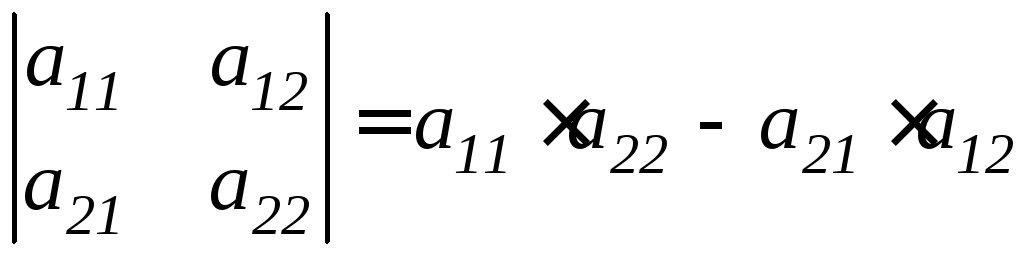Определителем 3-его порядка, соответствующим квадратной матрице А=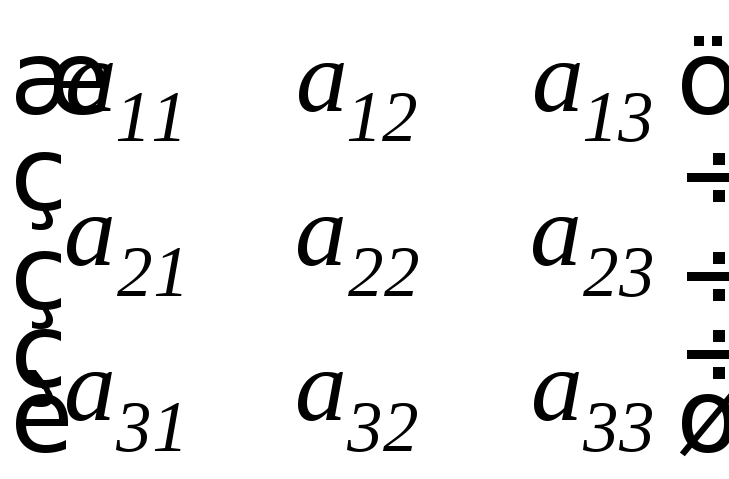, называется число

|А|= .

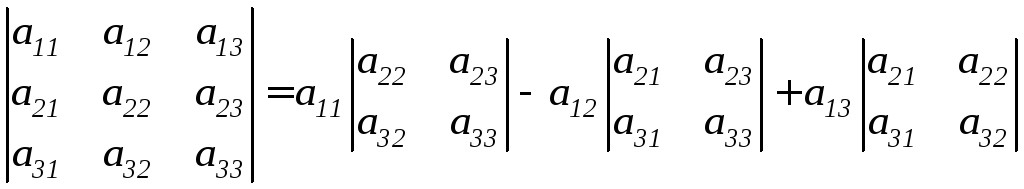Минором М_ij элемента а_ij называется определитель, полученный из данного определителя вычеркиванием i - строки и j- столбца. Так, минором М₂₃ определителя 3-его порядка является определитель М₂₃=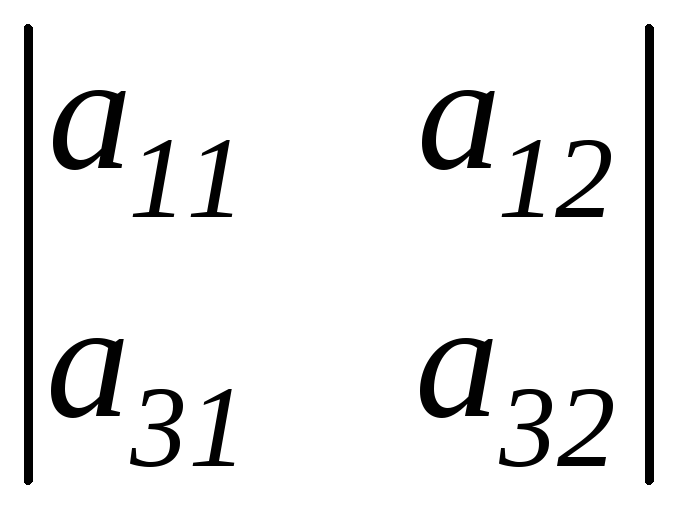, схема:.

Алгебраическим дополнением А_ij элемента а_ij определителя называется определитель, равный А_ij = (-1)^i+j М_ij.

Вычисление определителя по элементам строки или столбца.

Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраические дополнения. Так, по элементам второй строки вычислим определитель 3-его порядка:

|А| =

.

Операции над матрицами.

Суммой двух матриц А = (а_ij) и В = (b_ij) называется матрица С =(с_ij), каждый элемент которой равен сумме соответствующих элементов матриц А и В.

с_ij= а_ij+b_ij i =1,2, … , m, j =1,2, … , n.

Произведением матрицы А = (а_ij) на число λ называется матрица λА=( λ а_ij ), где каждый элемент матрицы А умножается на число λ.

Произведением матрицы А = (а_ij)_mn на матрицу В = (b_ij)_nk называется матрица С=(с_ij)_mk=AB , элемент с_ij которой равен сумме произведений соответствующих элементов i -ой строки матрицы А и j -ого столбца матрицы В.

Так, например,

.

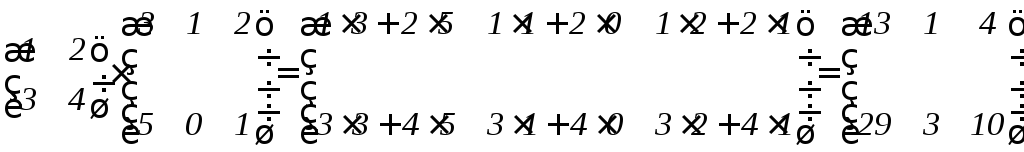Квадратная матрица А называется вырожденной, если ее определитель |А| = 0, и невырожденной , если |А| ≠ 0.

Обратной для невырожденной матрицы А называется матрица А^-1 такая, что , гдеЕ – единичная матрица (по главной диагонали которой стоят единицы, а остальные элементы равны 0).

Так, обратная матрица А^-1 для квадратной матрицы А 3-его порядка имеет вид

_.

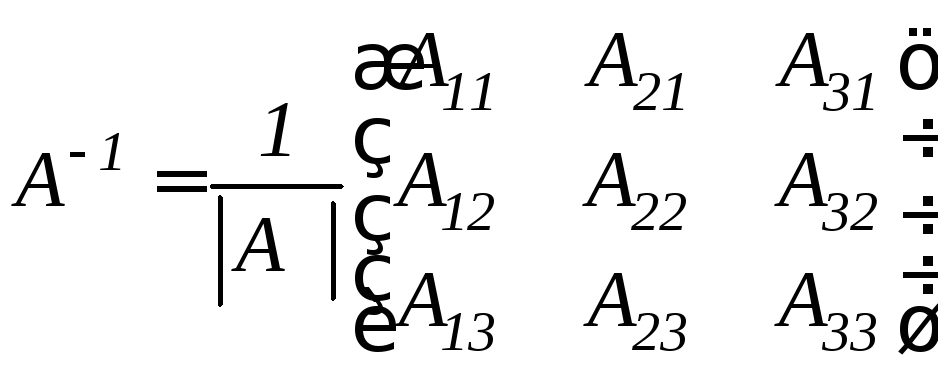1.2. Решение систем линейных уравнений

Правило Крамера. Рассмотрим систему трех уравнений с тремя неизвестными

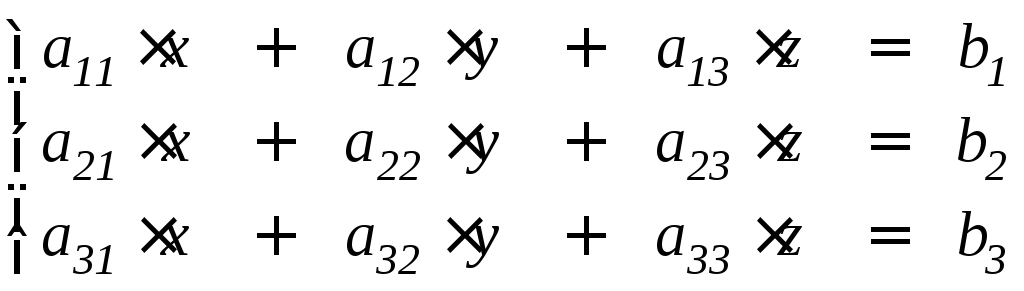. (1.1)

Решение находится по формулам Крамера

,

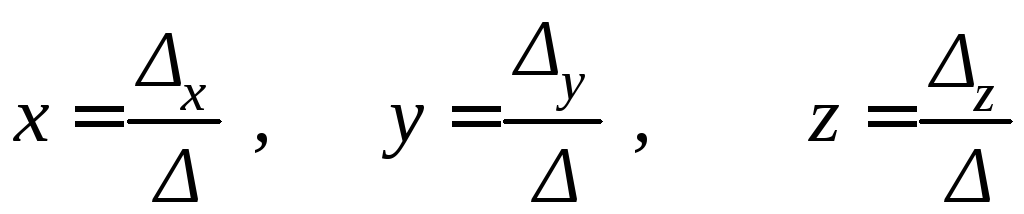где ,,

, .

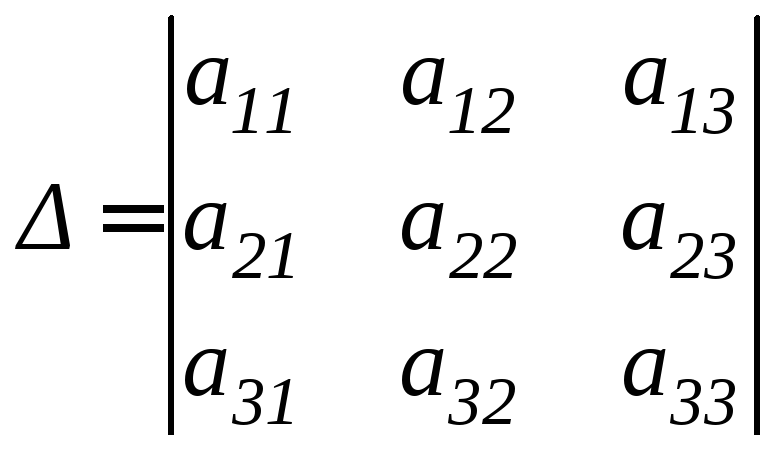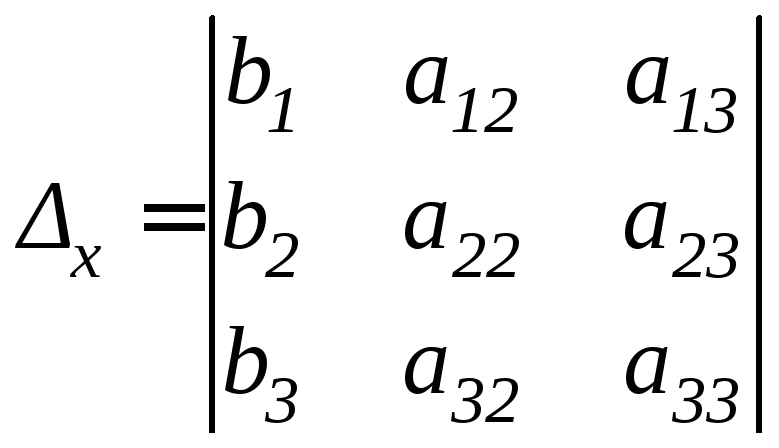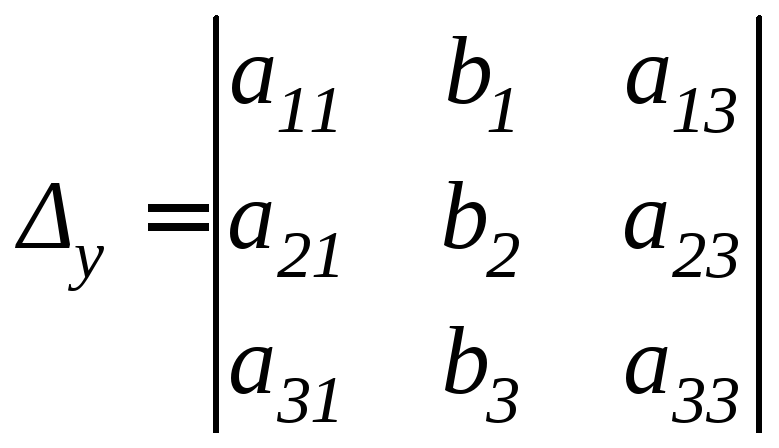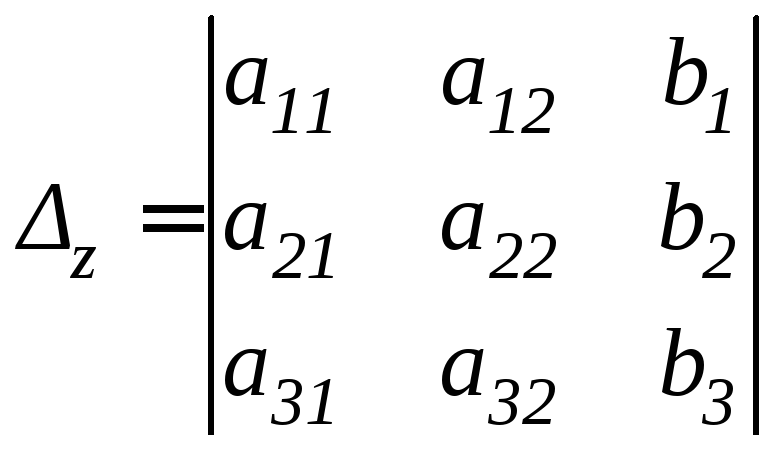Система имеет единственное решение при ∆ ≠ 0,множество решений при∆ = ∆_x = ∆_y = ∆_z = 0и не имеет решения при∆ = 0и хотя бы одном∆_x , ∆_y, ∆_z , не равном нулю.

Пример. Решить по правилу Крамера систему:

.

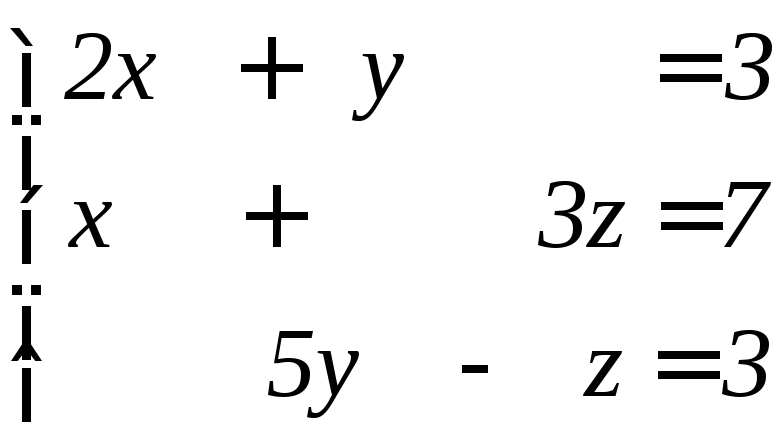Решение.

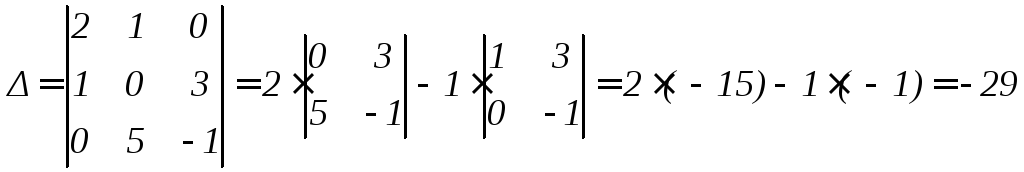
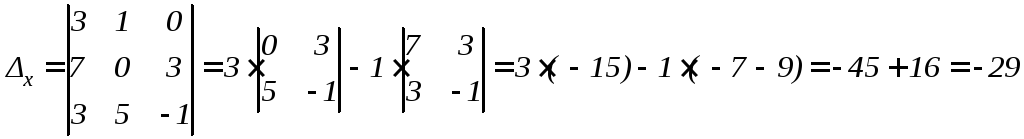
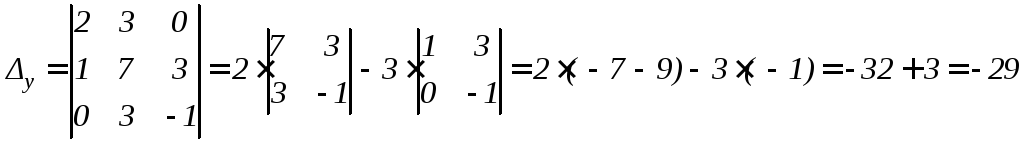
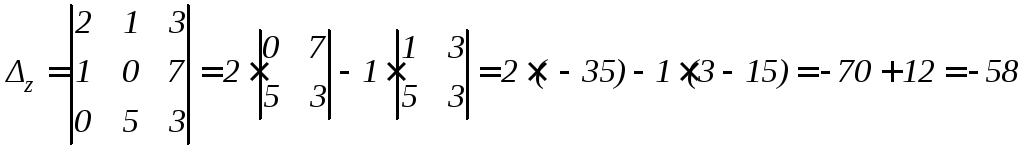
По формулам Крамера

.

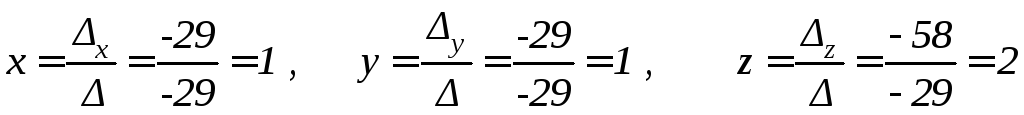Матричное решение системы линейных уравнений. Систему линейных уравнений (1.1) можно представить в матричном виде _{, где} ,,.

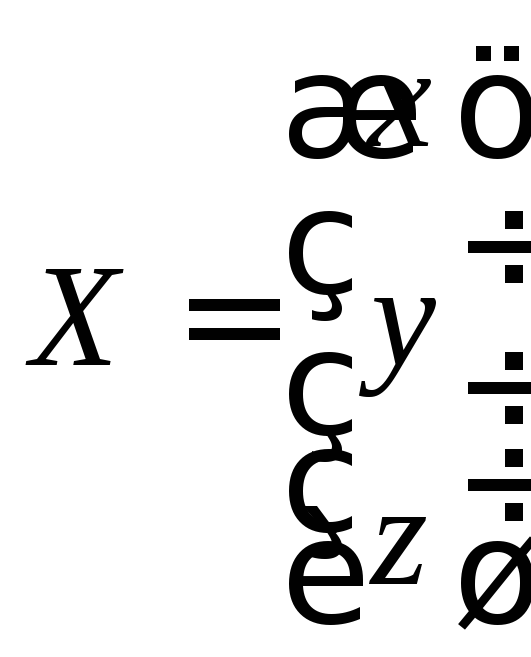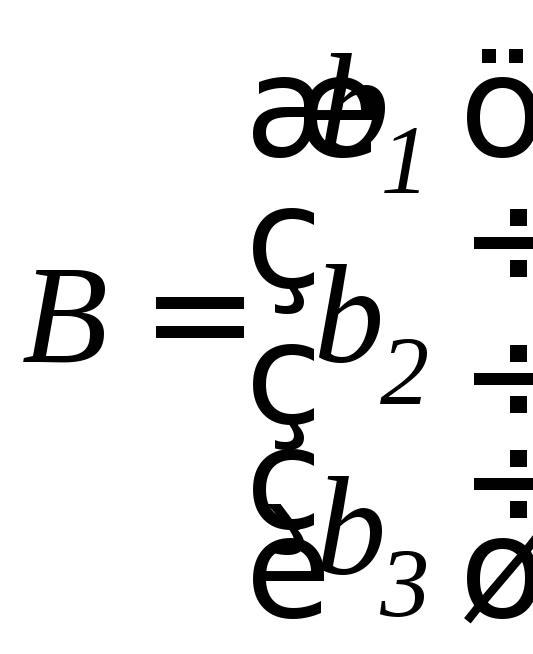Если матрица А невырожденная, то , умножая слева матричное уравнение на матрицу А^-1 , обратную А , получим , т.к.и, то.

Пример. Решить с помощью обратной матрицы:

.

Решение.

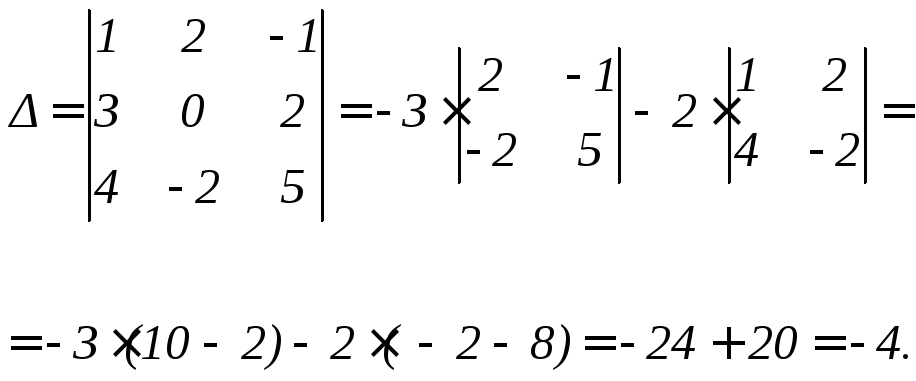
Найдем алгебраические дополнения соответствующих элементов матрицы А.

.

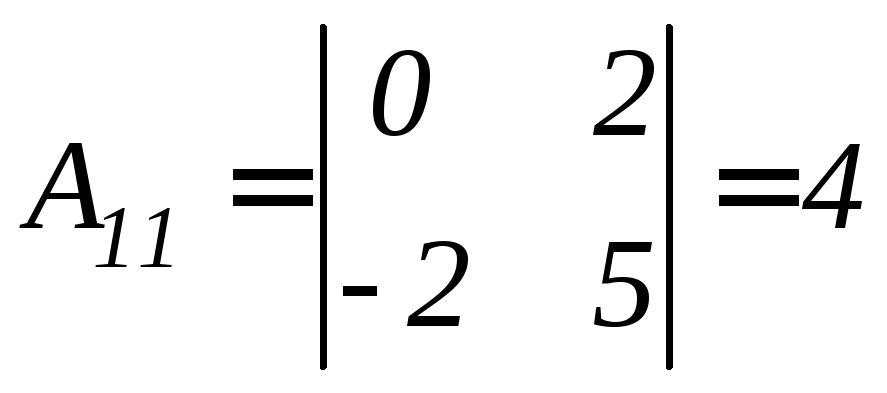
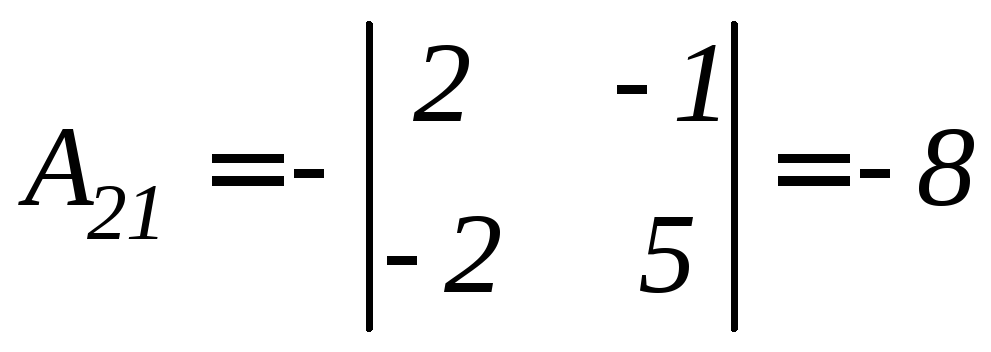
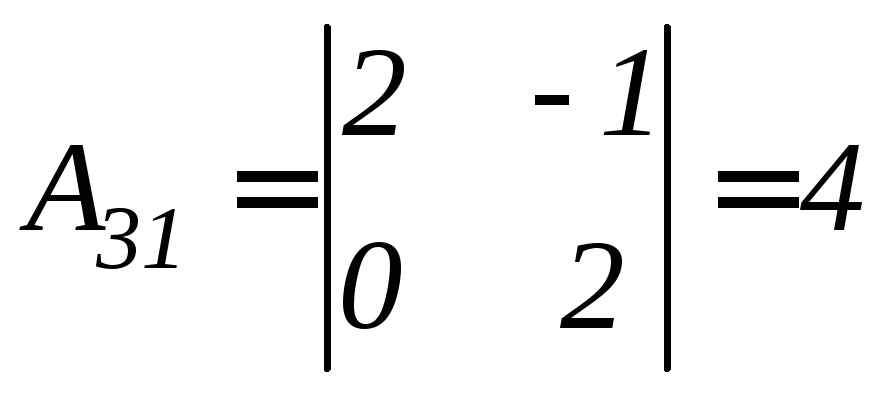
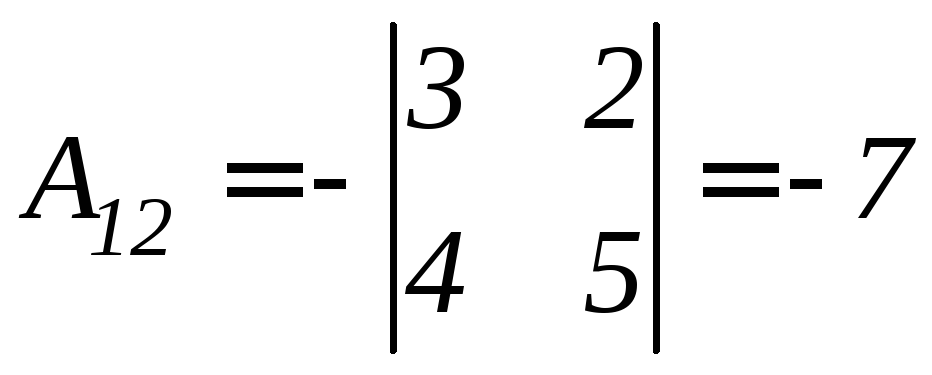
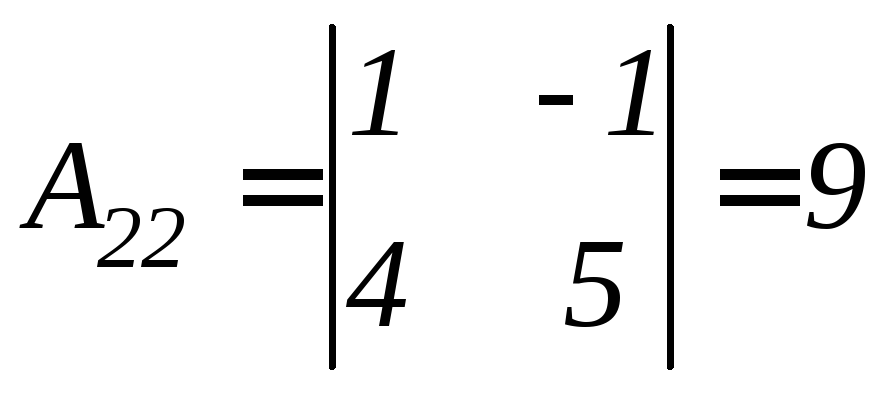
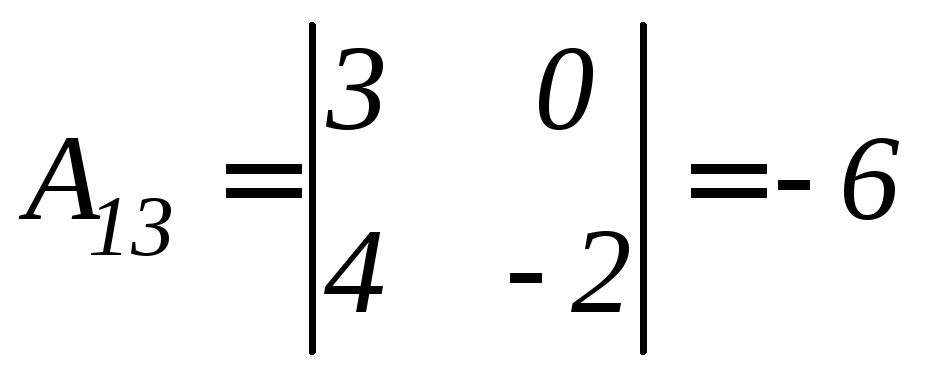
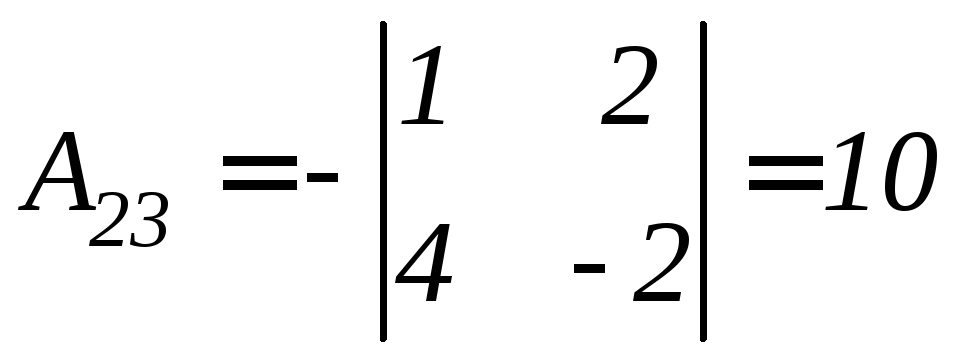
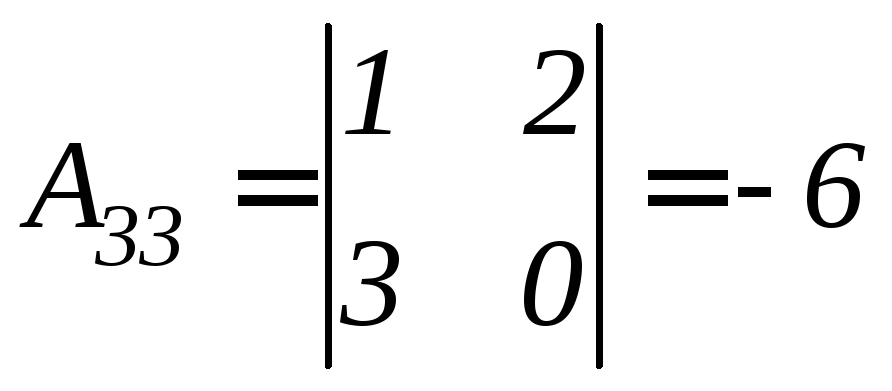Обратная матрица имеет вид .

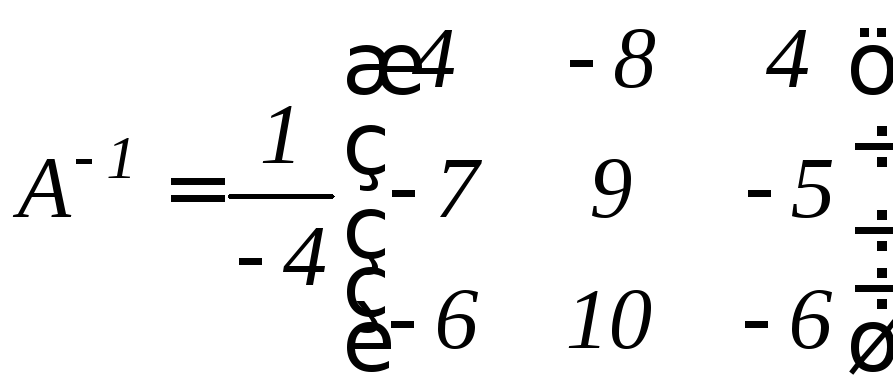Находим решение .

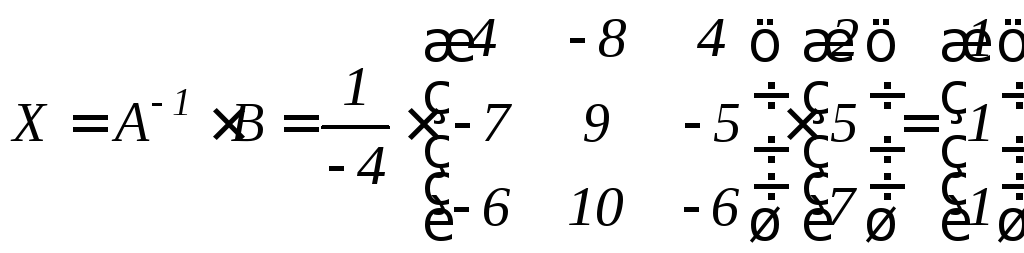Таким образом, система имеет решение x = 1, y = 1, z = 1.

Метод Гаусса. Элементарными преобразованиями системы уравнений называют следующие преобразования:

1. перемена местами двух любых уравнений;

2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;

3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Две совместные системы уравнений называются равносильными, если каждое решение одной является решением другой и обратно.

Элементарные преобразования переводят систему в равносильную данной.

Пример. Решить методом Гаусса систему:

Решение. Сначала умножим первое уравнение на (–2) и сложим со вторым , затем первое уравнение умножим на (-5) и сложим с третьим , в результате получим систему:

.

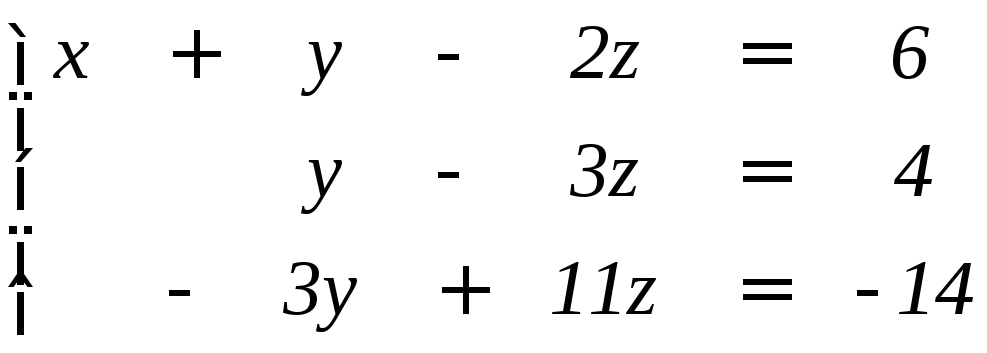Далее умножим второе уравнение на (+ 3) и сложим с третьим:

.

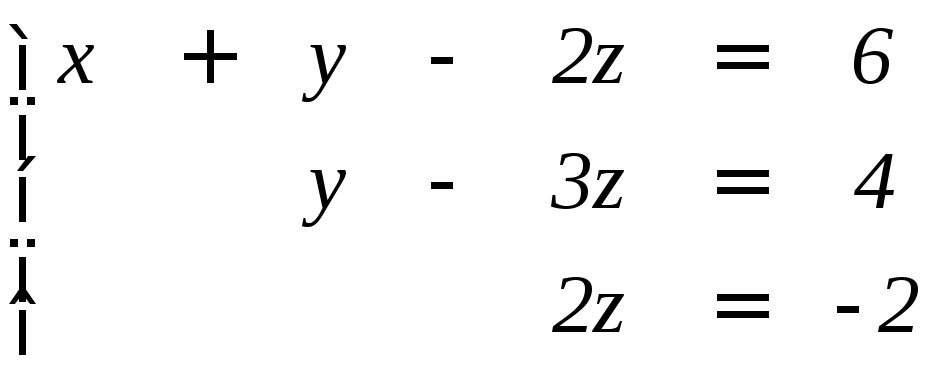Из этой системы последовательно находим

z = -1 y = 4 + 3z = 1 x = 6 + 2z – y = 6 – 2 – 1 = 3.

Итак, первоначальная система с помощью элементарных преобразований приведена к равносильной системе, имеющей треугольный вид и единственное решение.

Пример. Решить методом Гаусса систему:

.

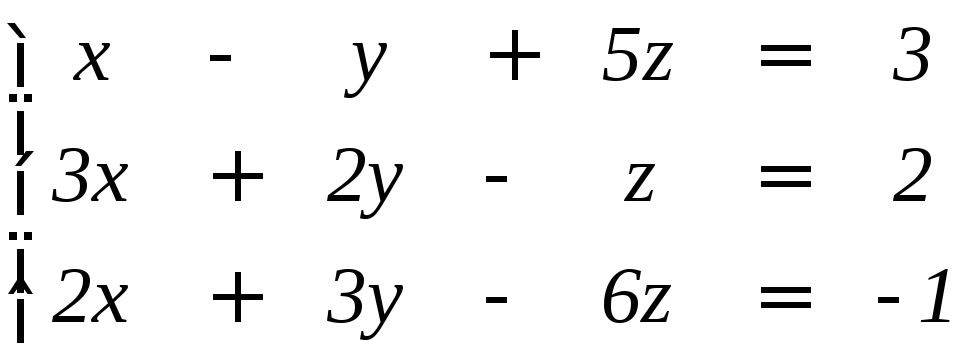Решение. Составим расширенную матрицу и выполним над ней элементарные преобразования:

~ ~.

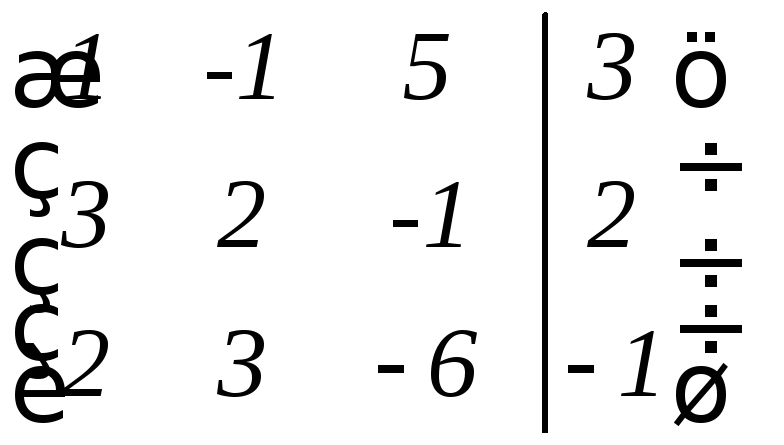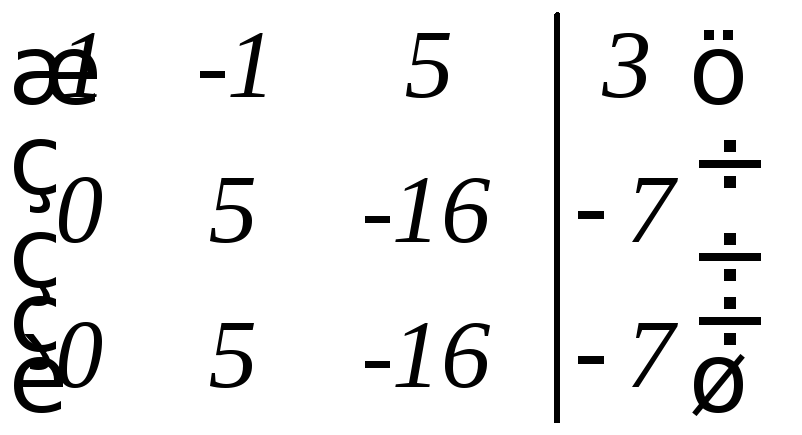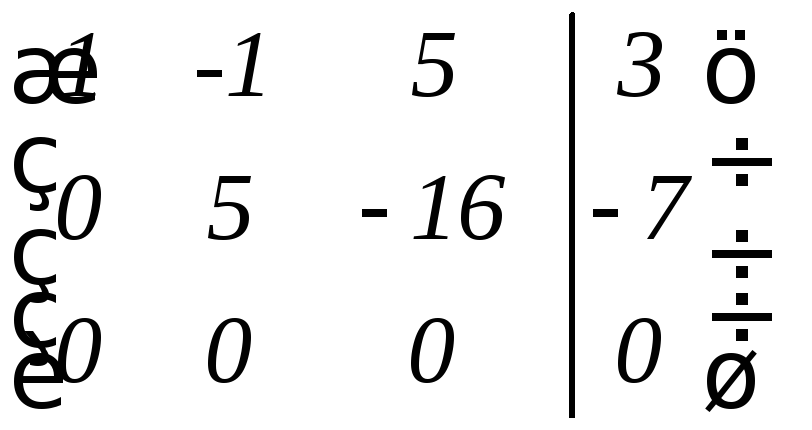Здесь первую строку умножили на (-3) и сложили со второй, далее - первую строку умножили на (-2) и сложили с третьей, а затем из третьей строки вычли вторую.