методичка з матем

Практичні завдання

Модуль1

Практичне заняття № 1

Матриці. Дії над матрицями. Визначники.

Короткі теоретичні відомості.

Матрицею називають таблицю упорядкованих чисел або будьяких інших об’єктів , розташованих в n рядках та m стовпцях.

Така матриця має вигляд

а1 1 а12	....а1n
	....a2 n		,
А= a21 a22
...................
am 1 am 2 ...am n

де аij - елементи матриці А, i- номер рядка, j- номер стовпця.

Добуток матриці А на число

	a	11	a	12	.... a	1n
	a 21 a 22				.... a 2 n
А	.......... .......... ....
	a m1 a m 2 .... a mn

Сума матриць А та В однакового розміру m n

a	b a	b	.....a	b
11	11 12	12	1n	1n
C=A+B= a21	b21a22	b22 ....a2n b2n			,
............................................
am1	bm1am2 bm2 ....amn bmn

де b ij - елементи матриці В

1

Обернена матриця

					A A ....A
					11	21	n1
A 1	1			A12		A22	....An2	,
	A			....................
					A A		....A
					1n	2n	nn

де Аij – алгебраїчні доповнення елементів аij, A 0

Практичні завдання

Дано

2 1		0		1 3 1
					2 0 4		Е-одинична матриця
A 1 1		2		B
	3 2	1
				1 2 3

Знайти:

1)2A 13 B

2)AT 4E

3)A B, B A

4)A , B , AB

5)A 1 , B 1

------------------------------------------------------------------------------

	3		5		2 3			1	2 1
Дано											Е – одинична матриця
	A				B			C 3 7 2
		4	1			2
					1				3 7
								2

6) Знайти:

а) значення матричного многочлена 2А+5В-Е, б) А В, В А

7)Знайти визначник матриці С. а) за правилом трикутника

б)розклавши за елементами 1-го рядка в) розклавши за елементами 1-ого стовпця

8)До матриці С знайти обернену.

2

Практичне заняття № 2 Розв'язування систем лінійних алгебраїчних рівнянь.

Формули Крамера. Матричний спосіб. Метод Гаусса.

Короткі теоретичні відомості.

Розглянемо СЛАР:

a

x

a

x

2

.... a

x

n

b

11

1

12

1n

1

a21 x1

a22 x2

.... a2n xn

b2

(1)

................................................

a

n1

x

a

n2

x

2

.... a

nn

x

n

b

1

Введемо позначення:

a

a ....a

x1

b1

11 12

1n

a

a

....a

A

X

x2

;

B

b2

21

22

2n

;

...................

.....

.....

a

....a

a

n1

n2

nn

x

n

b

n

Тоді систему (1) можна записати в матричному вигляді:

А Х=В (2)

Правило Крамера: Якщо основний визначник A

неоднорідної системи n лінійних алгебраїчних рівнянь з n невідомими недорівнює 0, то ця система має єдиний розв”язок, який знаходиться за формулами:

A

X k Ak , к=1,2..., де A k допоміжний визначник, який

одержується шляхом заміни k-ого стовпця визначника A

стовпця вільних членів.

Для розв'язування СЛАР (1) матричним методом, потрібно:

1.Перевірити виконання трьох вимог правила Крамера; 2.Знайти обернену матрицю A 1 до матриці А;

3

3.Знайти розв”язок Х шляхом множення оберненої матриці A 1 та матриці–стовп ця В вільних членів заданої системи, тобто за формулою X A 1 B

Розв'язувати будь-які системи лінійних алгебраїчних рівнянь можна методом Гаусса (виключення невідомих).

Суть методу Гаусса – зведення системи шляхом елементарних перетворень до такого вигляду системи, коли усі коефіцієнти, що знаходяться нижче головної діагоналі основної матриці, дорівнюють нулю.

Практичні завдання

1.Розв'язати систему рівнянь за формулами Крамера та матричним способом:

2x y z 2 а) 5x y 3z 142x y 2z 5

x y 3z 5 б) 2x 3y z 03x 2 y z 5

2.Розв'язати систему рівнянь за формулами Крамера та методом Гаусса:

x1 3x2 2x3 6		3x1 2x2 x3 5
а) 2x1 x2 3x3	4	б) x1 x2 x3 0
	0
3x1 4x2 x3		4x1 x2 5x3 3
3.Розв'язати систем у рівнянь методом Гаусса:
x1 2x2 x3 x4 2		x1 3x2 x3 14
а) 2x1 6x2 3x3 2x4 3		б) 3x1 2x2 5x3 4
			32
3x1 4x2 2x3 3x4 7		x1 8x2 3x3

-------------------------------------------------------------------------

-----

4

4.Розв'язати СЛАР: за формулами Крамера, матричним способом , методом Гаусса.

x1 5x2 x3 3 а) 2x1 4x2 3x3 23x1 x2 3x3 7

3x 2 y z 2 б) x 3y 2z 12x y 3z 5

5

Практичне заняття №3 Вектори. Дії над векторами. Поняття базису.

Скалярний добуток векторів.Скалярний добуток векторів.

Короткі теоретичні відомості

Координати x,y,z вектора початком якого є т.А (x1 y1 z1), а кінцем т. В(x2 y2 z2), дорівнюють різниці відповідних координат його кінця В і початку А: х=х2 – х1; у=у2 – у1; z=z2 – z1.

Довжину

(модуль)

вектора

a x_

y

z

визначають

за

1

1

1

формулою:

x2

y 2 z 2

a

1

1

1

Скалярний добуток

двох векторів

і

:

a b

a

b

cos

або

xa xb ya yb

za zb

a

b

a

b

a

b

a

b

Косинус кута між векторами

і

a

b

xa xb ya yb za zb

cos cos a,b

xa2 ya2 za2 xb2

yb2 zb2

Проекція вектора

на вектор

:

a

b

a

b

b

a

b

Умова колінеарності двох векторів

та

:

xa

ya

za

a

b

xb

yb

zb

Умова

перпендикулярності

двох

векторів

та

a

b xa xb ya yb za zb 0

Будь-яка трійка некомпланарних векторів a,b, c утворює базис в просторі і довільний вектор d простору можна подати в цьому базисі, як лінійну комбінацію d a b c або в координатній формі:

6

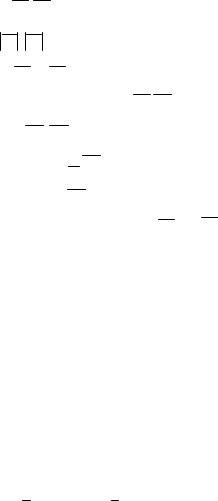
dx ax bx cx

dy ay by cydz az bz cz

Практичні завдання

1. Дано координати точок А=(2;3;6), В=(1;1;3), С=(0;2;1), D=(6;-3;5)

Знайти: а) AB,CD

б) AB , CD

в) 3AB 2CD

г) скалярний добуток AB AC

д) cos ( AB, AC )

е) проекцію AC AB

є) проекцію AC на вісь ox, oy, oz.

ж) перевірити чи вектори AC та BD будуть колінеарні,

перпендикулярні

2. Вектори

та

утворюють кут

2 ,

a

3;

b

4 .

a

b

Обчислити: а)

3

a

b

б) 3

2

2

a

b

a

b

в)

a

b

3. Знайти кут між діагоналями паралелограма, побудованого на векторах a (2,1,0) та b (0, 2,1)

7

4.Визначити лінійну залежність чи незалежність векторів: a1 1, 2, 5 , a2 5, 2,4 , a3 4,2, 3

5.Довести , що вектори a1 5,4,3 , a2 3, 1,2 , a3 3,1,3

утворюють базис в Е3 , розкласти вектор d 12,9,10 за цим базисом і знайти його довжину в цьому базис

6.Виконати завдання 1) якщо координати точок А(2;-3;4),

В(6;-2;2), С(1;-2;0), D(2;-1;3)

7.Дано вектори a 1,2,5 ,b 1,6,3 , c 0,0,2 , d 1,0,4 . Чи є

вектор d лінійною комбінацією векторів a,b, c ? Якщо так, знайти коефіцієнти лінійної комбінації.

8

Практичне заняття №4 Типи добутків векторів (векторний, мішаний). Їх

застосування.

Короткі теоретичні відомості

Векторний добуток векторів:

c a b ab sin , (a,b)

або через декартові координати

					i		j			k
					xa		ya za
	a		b
					xb		yb		zb

Мішаний (векторно-скалярний) добуток векторів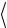: (a b) c a b c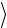

або через декартові координати:

xa ya za a,b, c xb yb zb xc yc zc

Площа паралелограма, побудованого на векторах a та b :

Sпар= a b

Площа трикутника АВС: S ABC 12 AB AC

Об”єм паралелепіпеда, побудованого на векторах a,b, c (з спільним початком:)

V 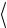a b c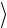

Об”єм піраміди ABCD:

VABCD 16 AB AC AD

9

Практичні завдання

1.Обчислити площу трикутника з вершинами А(1,1,1),

В(2,3,4), С(4,3,2).

2.	Показати , що вектори			2,5,7 ,		1,1, 1 ,		1,2,2
			a		b		c
	компланарні
3.	Знайти об”єм трикутної піраміди з вершинами
	а)	A(2,2,2), B(4,3,3), C(4,5,4), D(5,5,6)
	б)	A(1,2,3), B(4,4,4), C(2,6,4), D(2,3,6)

4.Знайти довжину висоти піраміди АВСD, що опущена з т. В на грань АСD, якщо

а) А(-1,3,-2), B(0,-1,2), C(-1,-2,-3), D(0,0,-1) б) A(2,4,-4), B(1,2,3), C(3,-2,1), D(0,3,1)

5.Перевірити чи будуть точки А(2,-1,-2), В(1,2,1), С(2,3,0), D(5,0,-6) лежати в одній площині.

6.Знайти довжину висоти трикутника BCD, що опущена з т.В

на сторону СD, якщо В(-2;0;4), С(1;-2;1), D(3;0;-1)

------------------------------------------------------------------------------

7.Знайти площу паралелограма побудованого на векторах a(1,2,3), b(3, 1,4) як сторонах

8.Знайти об”єм тетраедра, побудованого на векторах a(1,0,1),b(1,4,1),c( 1,1,1) як сусідніх ребрах.

9.У тетраедрі з вершинами А(1,3,-3), В(2,4,-2), С(3,1,5), D(4,0,1) знайти об”єм V, площу грані SABC, довжину висоти опущеної з вершини Д на грань АВС, кут між ребрами АВ і АС.

10