Федеральное агентство по образованию ГОУВПО «Уральский государственный технический университет – УПИ»

А.Б. Соболев, А.Ф. Рыбалко

МАТЕМАТИКА

Курс лекций для технических университетов

Части 1 и 2

Екатеринбург

2005

УДК 51/075.8 ББК 22.1я73

С54

Рецензенты:

зав. кафедрой физики УГЛУ, доктор физ-мат. наук, проф. М.П. Кащенко, зав. лабораторией ИФМ УрО РАН, доктор физ-мат. наук, проф. А.П. Танкеев

А.Б. Соболев, А.Ф. Рыбалко

С54 Математика: Курс лекций для технических вузов / А.Б. Соболев, А.Ф. Рыбалко. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. 359 с.

ISBN 5-321-00532-Х

Курс лекций по дисциплине ЕН.Ф.01 «Математика» предназначен для студентов, изучающих данную дисциплину в объеме 540 – 800 часов в течение 4 семестров. Содержание лекций соответствует ГОС и рабочим программам технических специальностей.

Первая часть включает 16 лекций и содержит материал, обычно изучаемый в первом семестре, – линейная алгебра, векторная алгебра, аналитическая геометрия, основы математического анализа (функции, пределы, производная).

Вторая часть включает 16 лекций и содержит материал, обычно изучаемый во втором семестре, – исследование функций, неопределенный и определенный интегралы, дифференциальные уравнения, дифференциальное исчисление функций нескольких переменных.

Электронная версия книги, используемая в аудиториях, сопровождается дополнительным иллюстративным материалом.

Наряду с курсом лекций существуют пособия, рассматривающие решение типичных задач и способствующие усвоению понятий и методов.

	ББК 51 (075.8)
	УДК 22.1я 73
ISBN 5-321-00532-Х	© ГОУ ВПО «Уральский государственный
	технический университете – УПИ», 2005
	© А.Б. Соболев, А.Ф. Рыбалко, 2005

ПРЕДИСЛОВИЕ

Курс лекций предназначен для студентов технических университетов и состоит из четырех частей, в которых излагается теоретический материал курса математики для инженеров.

Впервой части излагаются следующие разделы: линейная алгебра, аналитическая геометрия, начала математического анализа (теория пределов и дифференцирование).

Во второй части излагаются следующие разделы: исследование функций, неопределенный и определенный интегралы, дифференциальные уравнения, дифференциальное исчисление функций нескольких переменных

Вначале каждой лекции приведены заголовки разделов. В совокупности эти заголовки образуют программу дисциплины и являются базой вопросов для тестовых и экзаменационных заданий. Звездочкой помечены разделы, предназначенные для более глубокого изучения. В конце каждой лекции приведен список ключевых понятий.

Влекциях студент найдет основные определения, формулировки теорем, примеры, демонстрирующие методы решения типичных задач. Если отсутствуют доказательства каких–либо утверждений, то формулировки результатов сопровождаются примерами, разъясняющими их смысл.

Втексте приняты следующие условные обозначения:

Оопределение

Ттеорема

Сследствие

!замечание

Лекции 1-2 ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ

В лекциях 1 – 2 излагаются элементы линейной алгебры, в них приведены первоначальные сведения о матрицах и определителях и их применении. Матричное исчисление широко применяется в различных областях математики (решение систем линейных уравнений, векторная алгебра, дифференциальные уравнения, теория вероятности), механики, электротехники, теоретической физики и т.д. Матричное исчисление позволяет в компактной форме получить решение реальных задач, содержащих большое количество переменных.

1.1. Понятие матрицы. Частные виды матриц 1.2.* Перестановки и подстановки 1.3.* Понятие определителя любого порядка

1.4.Определители второго и третьего порядка

1.5.Свойства определителей

1.6.Теорема о разложении определителя по строке (столбцу)

1.7.Методы вычисления определителя n-го порядка

1.7.1.Метод понижения порядка

1.7.2.Метод сведения к треугольному виду

2.1.Операции над матрицами

2.2.Обратная матрица. Теорема о существовании левой и правой обратной матрицы. Алгоритм нахождения обратной матрицы

2.3.Решение матричных уравнений

2.4.Ранг матрицы. Метод окаймляющих миноров. Элементарные преобразования матриц

Ниже будут использоваться сокращенные способы записи сумм и произведений большого количества элементов:

n	n
∑aj = a1 + a2 +…+ an ,	∏aj = a1 a2 … an .
j=1	j=1

1.1. Понятие матрицы. Частные виды матриц

О

Матрицей размерности m ×n называется прямоугольная таблица чисел

aij

a11

a12

...

a1n

a

a

...

a

A =

a

m,n

= (a )

m,n

=

21

22

2n ,

ij

ij

... ...

...

...

a

m1

a

m2

...

a

mn

6 Лекции 1-2

где i =1,...,m; j =1,...,n , расположенных в m строках и n столбцах. Числа aij называют элементами матрицы. Числа i, j - индексы элемента матрицы, указывающие его местоположение: i - номер строки, j - номер столбца. Число

элементов матрицы m ×n определяется как произведение числа строк m на число столбцов n .

Частные виды матриц

О	Нулевой матрицей размерности m ×n называется матрица, все эле-
				0	0	0
				0	0	0
	менты которой равны нулю, например: =						.
				0	0	0
	Матрица размерности 1×n	называется матрицей-строкой или просто
О
	строкой, например: B = (2	1 7,3)1,3 .
	Матрица размерности m ×1 называется матрицей-столбцом или просто
О
		7
	столбцом, например: C = 3,5		.
		0
			3,1

ОМатрица называется квадратной, если число ее строк равно числу столбцов, m = n . Число n называется порядком матрицы, например при n=3:

	3	1	2
	0	7	0
D =				.
	4	5	1
				3,3

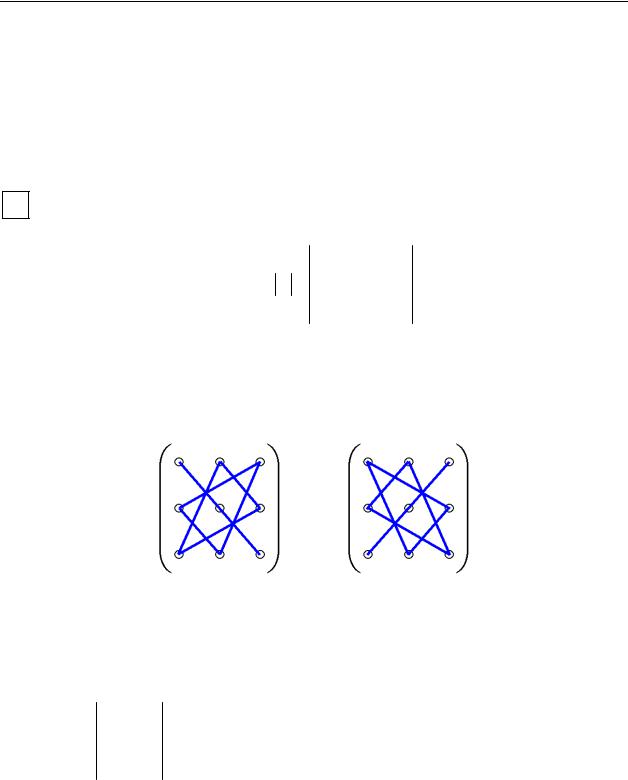
ОГлавной диагональю квадратной матрицы называется диагональ, составленная из чисел a11,a22 ,...,ann , идущая из левого верхнего угла в правый нижний; побочной называется диагональ, идущая из правого верхнего угла в левый нижний:

.

Определители и матрицы

7

ОКвадратная матрица называется диагональной, если все элементы, стоящие выше и ниже главной диагонали, равны нулю:

	6	0	0
	0	2	0
A =				.
	0	0
			−11

ОКвадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону главной диагонали, равны нулю:

		4	1	2
		0	7	5			- верхняя треугольная матрица;
D =
		0	0	1
	3		0	0
	6		−2	0			- нижняя треугольная матрица.
D =
	4		−8	1

ОКвадратная диагональная матрица с единичными элементами называется единичной и обозначается буквой Е.

Например, единичная матрица 3-го порядка имеет вид:

	1	0	0
	0	1	0
E =				.
	0	0	1

ОТранспонированием матрицы называется преобразование, состоящее в замене строк столбцами с сохранением их номеров.

Таким образом, строки данной матрицы будут в той же последовательности столбцами транспонированной матрицы, и наоборот.

	1	2	3					1	4
					,	T		2	5
A =	4	5	6			A	=			.
								3	6

В случае квадратной матрицы транспонирование сводится к повороту матрицы на 180˚ вокруг главной диагонали.

8	Лекции 1-2

1.2. * Перестановки и подстановки

ОПерестановкой n символов a1 ,a2 ,...,an называется любое расположение этих символов в определенном порядке.

Так как данные n символов можно занумеровать числами 1,2,...,n , то изучение пе-

рестановок любых n символов сводится к изучению перестановок этих чисел. Число всех перестановок из n чисел равно n! =1 2 3 ... n (читается: « n -факториал»).

Пример:

Все перестановки чисел 1, 2, 3 имеют вид: 123, 132, 213, 231, 312, 321.

Число их 3! = 6.

ОДва числа в перестановке образуют инверсию, если большее число стоит впереди меньшего, и образуют порядок, если меньшее число стоит впереди большего.

Способ подсчета числа инверсий: читаем числа перестановки в порядке их записи (слева направо), для каждого из чисел считаем, сколько чисел, меньших данного, стоит правее него, и все полученные числа складываем.

Пример:

В перестановке 528371964 число инверсий равно

4 + 1 + 5 + 1 + 3 + 2 + 1 = 17.

ОПерестановка называется четной или нечетной, смотря по тому, будет число инверсий в ней четно или нечетно.

ОТранспозицией называется перемена местами двух чисел перестановки. Транспозиция чисел i и j обозначается через (i, j). От любой перестановки n чисел к любой

другой перестановке тех же чисел можно перейти путем ряда транспозиций, причем можно обойтись не более чем n −1 транспозициями.

Пример:

От перестановки 25134 к перестановке 42513 можно перейти путем четырех транспозиций: (2,4),(2,5),(1,5),(1,3).

ОПодстановкой n чисел 1, 2, … n, или подстановкой n-й степени, называется вза-

имно однозначное отображение совокупности этих чисел на себя, т.е. такое отображение, при котором каждому числу от 1 до n соответствует одно из этих чисел и двум различным числам всегда соответствуют два различных числа.

Подстановка записывается двумя строками в общих скобках, причем каждому числу верхней строки соответствует стоящее под ним число нижней строки.

Например,		2 1 3 4		обозначает подстановку, в которой 1 →1,	2 → 3 , 3 → 4 ,
		3 1 4 2

4 → 2 . Иначе можно сказать, что подстановка n-й степени – это соответствие между двумя перестановками n чисел.

Определители и матрицы												9
В зависимости от расположения чисел в верхней строке одну и ту же подстановку
можно записывать многими способами.
Например, записи	1	2	3	2	3	1		,	3	2	1	обозначают одну и ту же
		3	,		1	2				3
	2		1	3					1		2

подстановку, в которой 1 переходит в 2, 2 в 3, 3 в 1. Каждая подстановка n чисел допускает n! различных записей. Число различных подстановок n элементов также равно n!.

ОПодстановка называется четной, если общее число инверсий в обеих ее строках четно, и нечетной, если нечетно. Иначе говоря, подстановка четна, если ее строки имеют одинаковую четность, и нечетна, если – противоположную четность.

1.3. * Понятие определителя любого порядка

Пусть дана квадратная матрица порядка n:

		a11		a12	...	a1n
A = (a )		a		a	...	a
		=	21	22	...	2n .
ij	n,n	... ...				...
		a		a	...	a
		n1		n2			nn

ООпределителем n -го порядка, или определителем матрицы A , при n >1 называ-

ется число, полученное из элементов этой матрицы по формулам:

a11

a12

...

a1n

A

=

aij

n,n =

a21

a22

...

a2n

= ∑(−1)s+t ai1 j1 ai2 j2 ...ain jn ,

... ... ... ...

an1

an2

...

ann

где сумма берется по всем различным между собой подстановкам

i1

i2

...

in

j

j

...

j

,

1

2

n

причем s - число инверсий в верхней, а t

- в нижней строке.

Слагаемые суммы называются членами определителя; каждый член опреде-

лителя равен произведению n

элементов матрицы, взятых по одному из каждой

строки и каждого столбца, причем это произведение берется со своим знаком, если подстановка индексов четна, и с противоположным, если нечетна.

Определитель первого порядка равен единственному своему элементу. Число всех членов определителя n -го порядка равно n !. Элементы, строки, столбцы и т. д. матрицы A называются соответственно элементами, строками, столбцами и т. д. определителя A .

10 Лекции 1-2

1.4. Определители второго и третьего порядка

О	Определителем квадратной матрицы A второго порядка называется
	число, равное det A =							a11	a12		= a a	22	− a	21	a .
								a21			11				12
									22
	Например,		1	2		=1 4 − 2 3 = −2 .
			3	4

ООпределителем квадратной матрицы А третьего порядка называется число, равное

a11 a12 a13 det A = A = a21 a22 a23 =

a31 a32 a33

= a11a22a33 + a12a23a31 + a21a32a13 − a13a22a31 − a21a12a33 − a32a23a11 .

Это выражение получается по правилу треугольников (правилу Саррюса), которое можно пояснить следующей схемой:

,

+

-

где элементы определителя изображаются кружками, а соответствующие произведения - отрезками или треугольниками. Знаки «+» и «-» соответствуют знакам слагаемых, входящих в определитель, например,

1 0 0

∆ = 1 2 1 =1 2 1 + 0 1 0 +1 3 0 −0 2 0 −1 3 1−1 1 0 = −1.

0 3 1

1.5. Свойства определителей

Сформулированные ниже свойства легко проверяются непосредственным вычислением определителей 2-го или 3-го порядков и остаются справедливыми для определителей порядка n .

Введем необходимые определения.

Определители и матрицы

11

ОСуммой нескольких строк одинаковой длины называется строка, каждый элемент которой равен сумме соответствующих элементов данных строк.

ОПроизведением строки на число называется строка, каждый элемент которой получен из соответствующего элемента данной строки умножением его на данное число.

ОЛинейной комбинацией нескольких строк одинаковой длины называется строка, равная сумме произведений данных строк на некоторые

числа, называемые коэффициентами этой линейной комбинации. Если одна строка является линейной комбинацией других, то говорят, что она линейно выражается через эти строки. Например, равенство (1, −1, −3, −5)= 3(1,1,1,1)− 2(1, 2,3, 4) означает, что первая строка является ли-

нейной комбинацией двух других.

1˚. При транспонировании определителя его значение не меняется. Свойство 1˚ устанавливает полное равноправие строк и столбцов определителя |A|. Иначе говоря, свойства определителей, доказанные для строк, верны и для столбцов, и наоборот.

2˚. При перестановке местами двух любых строк (столбцов) определитель меняет знак.

3˚. Определитель, имеющий две одинаковые строки (столбца), равен 0. Из 2˚: при перестановке строк ∆ = −∆, ∆ + ∆ = 0 , 2∆ = 0 ∆ = 0 .

4˚. Общий множитель любой строки (столбца) можно выносить за знак определителя.

Это свойство можно сформулировать иначе: умножение всех элементов некоторой строки (столбца) определителя |A| на число k равносильно умножению определителя на это число, например,

2	1	2	= 2	1	1	2
4	3	4		2	3	4	.
6	5	6		3	5	6

5˚. Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю. Это свойство вытекает из предыдущего при k = 0.

6˚. Если все элементы одной строки (столбца) определителя пропорциональны соответствующим элементам другой строки (столбца), то он равен нулю.

7˚. Если всякий элемент любой строки (столбца) представляет собой сумму двух слагаемых, определитель равен сумме двух определителей, в пер-

12	Лекции 1-2

вом из которых в соответствующей строке (столбце) оставлены первые слагаемые, а во втором – вторые, например,

1	2	3		1	2	3		1	2	3		1	2	3
4	5	6	=	1 + 3 3 + 2 5 +1			=	1	3	5	+	3	2	1	.
7	8	9		7	8	9		7	8	9		7	8	9

8˚. Если к элементам любой строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на любое число, то он не изменится.

Пользуясь свойством 8˚, можно все элементы некоторой строки (столбца) определителя, кроме одного, сделать равными нулю, не меняя при этом величину определителя.

1.6. Теорема о разложении определителя по строке (столбцу)

					a11	a12	...	a1n
Рассмотрим определитель n -го порядка		A		=	a21	a22	...	a2n	.
					... ... ... ...
					an1	an2	...	ann

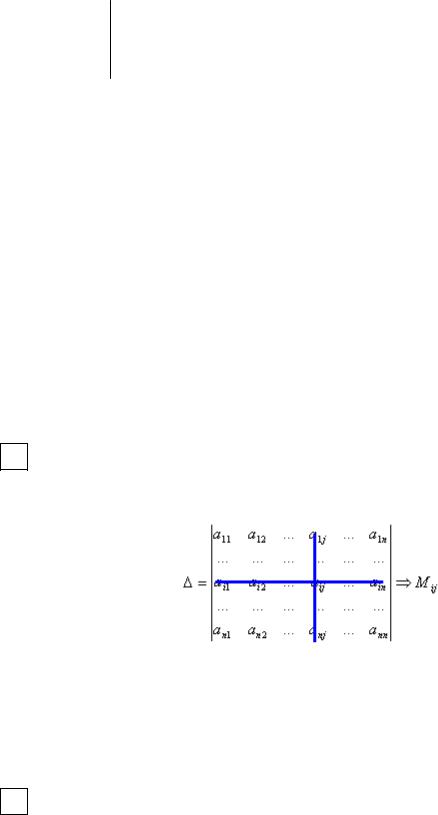
ОМинором Мij элемента аij определителя n-го порядка называется определитель (n-1) порядка, полученный из исходного вычеркиванием i-строки и j–столбца, на пересечении которых стоит элемент aij.

.

Например, ∆ =	1	2	3		4	5		1	3
	4	5	6	, M13 =			, M32 =			.
	7	8	9		7	8		4	6

ОАлгебраическим дополнением Аij элемента аij называется его минор со знаком (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент aij, Aij = (−1)i+ j Mij , например,

Определители и матрицы

13

A13 = (−1)1+3 M13 = (−1)4 M13 = M13 , A32 = (−1)3+2 M32 = (−1)5 M32 = −M32 .

ТОпределитель n-го порядка |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические

дополнения:

n

det A = ∑aij Aij = ai1 Ai1 + ai2 Ai2 +... + ain Ain , i =1,..., n , i=1

n

det A = ∑aij Aij = a1 j A1 j + a2 j A2 j +... + anj Anj , j =1,..., n . i=1

Эти формулы представляют собой разложение определителя по i-й строке и по j-му столбцу. Например, для определителей третьего порядка разложение по первому столбцу имеет вид:

a11

a12

a13

a21

a22

a23

= a11 A11 + a21 A21 + a31 A31 =

a31

a32

a33

= a

a22

a23

− a

a12

a13

+ a

a12

a13

=

11

a

a

21

a

a

31

a

a

32

33

32

33

22

23

=a11a22a33 + a12a23a31 + a21a32a13 − a13a22a31 − a21a12a33 − a32a23a11 .

САлгебраическая сумма произведений элементов любой строки (столбца) определителя |A| на алгебраическое дополнение соответствующих эле-

n

ментов другой строки (столбца) равна нулю: ∑Aij akj = 0,k ≠ i .

j=1

Непосредственным вычислением показывают, что этой сумме соответствует определитель с двумя одинаковыми строками (столбцами).

1.7. Методы вычисления определителя n-го порядка

Определители высшего порядка вычисляются с использованием их свойств двумя способами.

14	Лекции 1-2

1.7.1. Метод понижения порядка

Так как в формуле разложения определителя n-го порядка по строке (столбцу)

n

detA= ∑aij Aij = ai1 Ai1 + ai2 Ai2 + ...+ ain Ain ,

j=1

все алгебраические дополнения являются определителями (n-1)-го порядка, то задача свелась к вычислению n определителей меньшего, (n-1)-го порядка.

Если в некоторой строке исходного определителя много нулей, то именно по ней удобно проводить разложение. Более того, используя свойство 8˚, можно добиться того, что все элементы некоторой строки (столбца), кроме одного, станут равны нулю.

1.7.2. Метод сведения к треугольному виду

Используя свойства 1˚– 8˚, добиваются такой структуры определителя, при которой все его элементы, стоящие выше (ниже) главной диагонали, равны нулю, т.е. определитель имеет треугольную форму и численно равен произведению элементов, стоящих на главной диагонали:

a11

A = ...0 0

a12 ... a1n a22 ... a2n

... ... ...

0 ... ann

n

= ∏aii =a11 a22 ... ann .

i=1

Пример:

Вычислить определитель ∆ =	1	0	0	двумя способами.
	1	2	1
	0	3	1

1). Разложим определитель по первой строке:
∆ =1 (−1)1+1						2 1								+ 0	(−1)1+2						1 1			+ 0 (−1)1+3				1 2				= 2 −3 = −1.
						3			1												0	1						0		3
2). Приведем определитель к треугольному виду:
		1	0	0				=			1			0	0		=		1			0		0		=1 2				−	1			= −1.
		1	2	1							0 2				1				0			2		1
																															2
		0	3	1							0			3	1				0			0		− 0,5

Определители и матрицы

15

2.1. Операции над матрицами

О Две матрицы A = (aij )m,n и B = (bij )m,n равны, A = B , если равны их размер-

О

О

ности и все их соответствующие элементы совпадают, aij = bij ,

i =1,...,m;			j =1,...,n .
Суммой двух матриц A = (aij )						m,n		и B = (bij )		m,n	одинаковой размерности m ×n
называется матрица C = (cij )
							,	C = A + B ,			все элементы которой равны
					m,n
cij = aij + bij ,			i =1,..., m;	j =1,..., n .
Свойства операции сложения:								1˚. A + B = B + A .
								2˚. A + B +C = (A + B) +C .
								3˚. A + = A .
								4˚. A +(−A) = .
Произведением матрицы A = (aij )									на число α называется матрица
B = (bij )									m,n
		,	B =α A,	все				элементы			которой равны bij =αaij ,
	m,n
i =1,...,m;			j =1,...,n .

Свойства операции умножения на число:

5˚. (α β)A =α(βA) . 6˚. α( A + B) =αA +αB . 7˚. (α + β) A =αA + β A . 8˚. 0 A = ; 1 A = A .

Для доказательства свойств 1˚-8˚ достаточно воспользоваться соответствующими определениями.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

О	Произведением матрицы A = (ail )m,n размерности (m ×n) на матрицу
	B = (blj )n,k размерности (n ×k ) называется	матрица	C = (cij )		= A B
				m,k
	размерности (m ×k ), элементы которой вычисляются по формуле:
	k
	cij = ∑ail blj = ai1 b1 j + ai2 b2 j +... + ail blj	i =1,..., m ,	j =1,...,k .

l=1

16	Лекции 1-2

Иначе: элемент, стоящий на пересечении i-й строки и j-го столбца матрицы произведения cij , равен сумме произведений элементов i-й строки

матрицы А на соответствующие элементы j-го столбца матрицы В.

Пример:
	1	3	, B =	1		9	10	B .
	Дано: A =				0	2	. Найти C = A
	2	4					1
	c11 =1 1+3 0 =1,					c12 =1 9 +3 2 =15 ,		c13 =1 10 +3 1 =13 ,
	c21 = 2 1+ 4 0 = 2 ,					c22 = 2 9 + 4 2 = 26 ,		c23 = 2 10 + 4 1 = 24 .
	1	15	13
	C =	26	.
	2		24

Свойства операции умножения матриц:

9˚. (A× B)×C= A×( B× C) (A× B)× C= A×( B× C). 10˚. (A+ B)× C = A× C+ B× C.

11˚. A×( B + C)= A× B+ A× C. 12˚. A×E=E× A= A.

13˚. A× = × A = .

14˚. (A×B)T = B T× AT.

15˚. det(A×B) = det A×det B .

Для доказательства свойств 9˚-14˚ достаточно воспользоваться определениями операций над матрицами.

ОМатрицы A и B называются перестановочными (коммутирующими),

если A×B=B×A. В общем случае произведение матриц не коммутативно, A×B≠B×A.

Определители и матрицы

17

2.2.Обратная матрица. Теорема о существовании левой и правой обратной матрицы.

Алгоритм нахождения обратной матрицы

О

Квадратная матрица A n–го порядка называется вырожденной, если оп-

ределитель этой матрицы равен нулю,

A

= 0 , и невырожденной, если

A

≠ 0 .

Матрица А-1 называется обратной матрицей для некоторой квадратной

О

матрицы А, если выполняется соотношение: A× A−1 = A−1 × A = E .

Теорема о существовании и единственности обратной матрицы.

Т

Если матрица A не вырождена, то существует, и притом единст-

венная, обратная матрица

A−1 , равная

A−1 =

1

( A )T , где A = (Aij )-

det A

присоединенная матрица (матрица, составленная из алгебраических до-

полнений элементов исходной матрицы).

Доказательство:

Пусть дана квадратная матрица порядка n :

a

a

...

a

11

12

1n

A = (a )

= a21

a22

...

a2n .

ij

n,n

... ...

...

...

an2

...

an1

ann

1. Доказательство существования (необходимость). Пусть существует

A−1 . По определению A−1 A = E . По свойству 15˚

операции умножения

матриц det( A−1 A) = det E ,

det A−1 det A = det E =1 det A ≠ 0 , то есть мат-

рица A не вырождена.

2.Доказательство существования (достаточность). Пусть матрица A

не вырождена. Найдем вид элементов A−1 , для чего вычислим произведение

C = A ( A )T = (aij ) (Aij )T ,

n	n	det A, i = j
cij = ∑aik ( AT )kj = ∑aik Ajk =
k =1	k =1	0, i ≠ j

по теореме о разложении определителя по строке (столбцу),

18												Лекции 1-2
det A		0	...	0			1	0	...	0
	0	det A ...		0			0	1	...	0
откуда C =						= det A						= det A E ,
		...	...	...				...	...	...
...						...
	0	0	...	det	A		0	0	...	1

т.е. A ( A )T = det A E .

Так как det A ≠ 0 ,		( A )T		−1	1					T
	A		= E и A		=		( A		)		.
		det A				det A

3. Доказательство единственности (от противного). Предположим, что кроме матрицы A−1 , для которой A−1 A = E , существует матрица B , для которой также B A = E , причем B ≠ A−1 . Вычтем из одного равенства другое:

A−1 A − B A = E − E = , ( A−1 − B) A =.

Умножив последнее равенство на A−1 справа, получим:

( A−1 − B) AA−1 = A−1 = .

Так как A A−1 = E , ( A−1 − B)E = , A−1 − B = , A−1 = B , что противоречит B ≠ A−1 . Предположение неверно, обратная матрица единственна.

!1˚. (A−1 )−1 = A .

2˚. (α A)−1 = α1 A−1 . 3˚. (A× B)−1 = B−1 × A−1 .

4˚. (A−1 )T = (AT )−1 .

Алгоритм нахождения обратной матрицы:

1.Находим det A , проверяем det A ≠ 0 .

2.Находим M ij - все миноры матрицы A .

3.Определяем Aij = (−1)i+ j Mij .

4.Строим матрицу алгебраических дополнений A = (Aij ) и транспониру-

ем: ( A )T = (Aji ).

5.Делим каждый элемент матрицы на det A : A−1 = det1 A ( A )T .

Определители и матрицы

19

Пример:

Найти матрицу, обратную для матрицы

1

2

A =

.

3

4

1. det A = 4 − 6 = −2 ≠ 0 .

2. M11 = 4, M12 = 3, M 21 = 2, M 22

=1.

3. A11

= 4, A12

= −3, A21

= −2, A22

=1.

4

−3

, ( A

)

T

4

−2

4. A

=

=

1

.

−2

1

−3

5. A−1 = −

1

4

−2

−2

1

=

.

−3

2

1

3 / 2

−0,5

Проверка:

1 2 −2

1 −2 +3 1−1

1 0

= E .

A A−1 =

−0,5

=

−6 +6

3 −2

=

0 1

3

4 1,5

2.3. Решение матричных уравнений

О

Если A , B - известные матрицы, а X – неизвестная, то равенство вида

A X = B называется матричным уравнением.

Основные типы матричных уравнений:

1.

A X = B . Матрица A должна быть квадратной,

A

≠ 0. Умножим уравне-

ние на A−1 слева: A−1 A X = A−1B , E X = A−1B ,

X = A−1B .

2.

X A = B . Матрица A должна быть квадратной,

A

≠ 0. Умножим уравне-

ние на A−1 справа: X AA−1 = B A−1 X = B A−1 .

3.

A X B =C . Матрицы A и B должны быть квадратными,

A

≠ 0,

B

≠ 0 .

Умножим на A−1 слева: A−1 A X B = A−1C X B = A−1C . Умножим на

B−1 справа: X B B−1 = A−1C B−1 X = A−1 C B−1 .

Пример:

Решить матричное уравнение: A X = B ,

1		2		;	3		5
где A =	3	4			B =	5	9	.

20																							Лекции 1-2
	X = A	−1	B ,		A	−1			1				( A	T	−2		1
							=							)	=	−0,5				,
								det			A
															1,5
		− 2					1					3		5	−1	−1		,	X			−1 −1
	A−1 B =														=						=		.
				1,5		− 0,5						5				3						2 3
														9	2

2.4.Ранг матрицы. Метод окаймляющих миноров. Элементарные преобразования матриц

Пусть в матрице A размерности (m ×n) выбраны k строк и k столбцов, причем k ≤ min (m,n). Тогда элементы, стоящие на пересечении выбранных

строк и столбцов, образуют квадратную матрицу k -го порядка. Определитель Mk этой матрицы называется минором k -го порядка матрицы A .

ОРангом матрицы A называется число, равное максимальному порядку r отличных от нуля миноров M k этой матрицы:

r = r (A)= rang A.

О Матрицы называются эквивалентными, что обозначается A B , если r (A)= r (B).

Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.

Метод окаймляющих миноров

Пусть в матрице A элемент aij ≠ 0 , тогда M1 ≠ 0 и r (A)≥1. Окаймляем этот элемент элементами ( j +1)-го столбца и (i +1)-й строки, получаем минор 2-го порядка:

M2 =	ai, j	ai, j+1	.
	ai+1, j	ai+1, j+1

Если M2 = 0 , то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка. Если все миноры второго порядка равны нулю, то r (A)=1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r (A)≥ 2 .

Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его

элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr ≠ 0 , но все Mr+1 = 0 .

Определители и матрицы

21

Пример:

1

−1

1

Найти ранг матрицы A =

2

− 2

2 .

1

1

−1

M

1

=1; M 1

=

1 −1

= −2 + 2 = 0 , M 2 =

−1 1

= −2 + 2 = 0 ,

2

2 −2

2

−2 2

M23 =

2 −2

= 2 + 2 = 4 ≠ 0 ; M 3 =

1

−1

1

= 0 r( A) = 2 .

2 − 2 2

1

1

1

−1

−1

Метод элементарных преобразований

Кэлементарным преобразованиям матрицы относятся следующие:

транспонирование;

перестановка строк (столбцов);

умножение строки (столбца) на число α ≠ 0 ;

прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число;

отбрасывание нулевой строки (столбца) матрицы.

ТЭлементарные преобразования матрицы не меняют ее ранга.

Для определения ранга матрицы A методом элементарных преобразований следует:

1.Переставить строки так, чтобы в верхнем левом углу матрицы был ненулевой элемент.

2.Все элементы первого столбца, кроме a11 , обратить в ноль:

a		...	a		a		a
	11		1n			11		1n
A =		...	a			0	a		.
a	m1					0
			mn					mn

3.Повторить операцию со второй строкой: во втором столбце должен быть ненулевой элемент, после чего все элементы второго столбца, кроме a12

и a22 , обратить в ноль.

Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:

22										Лекции 1-2
a11		a12 ...			a1,r−1		a1r	...	a1n
	0	a	22	...	a	2,r−1	a	...	a
							2r		2n
A = ... ... ...						...	...	... ...		.
	0	0 ...			a	−1,r−1	a	...	a
					r		r−1,r		r−1,n
	0	0 ...				0	a	...	a
							rr		rn

Тогда ранг матрицы A = r (A)= rang A = rang A.

В результате изучения материала, изложенного в этих лекциях,

устудентов должны сформироваться следующие понятия:

матрица - таблица,

определитель - число,

ранг матрицы - число,

минор,

алгебраическое дополнение.

Студент должен уметь:

вычислять определители 2-го, 3-го и n -го порядков,

перемножать матрицы,

находить обратную матрицу,

определять ранг матрицы,

решать матричные уравнения.

Лекция 3 СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

В лекции 3 излагаются элементы теории систем линейных уравнений. Системы линейных уравнений возникают при решении многих задач механики, электротехники, теоретической физики и т.д. Матричное исчисление позволяет в компактной форме получить решение таких систем. Реальные задачи, содержащие большое количество переменных (десятки и сотни), требуют владения этими методами.

3.1.Системы m линейных уравнений с n неизвестными. Основные определения

3.2.Системы n линейных уравнений с n неизвестными. Матричный метод решения. Правило Крамера. Метод Гаусса (метод последовательного исключения переменных)

3.2.1.Системы n-линейных уравнений с n неизвестными

3.2.2.Правило Крамера

3.2.3.Метод Гаусса

3.3.Теорема Кронекера - Капелли

3.4.Однородные системы линейных уравнений

3.5.Схема отыскания общего решения системы m уравнений с n неизвестными

3.6.* Фундаментальная система решений

3.1.Системы m линейных уравнений с n неизвестными. Основные определения

Рассмотрим систему линейных уравнений (СЛУ), содержащую m уравнений и n неизвестных:

a11x1 + a12 x2 +…+ a1n xn = b1,
a21x1 + a22 x2 +…+ a2n xn = b2 ,
…………………………………,				(1)
a x	+ a x	+…+ a x	= b .
m1 1	m2 2	mn n	m
где aij , i =1,..., m; j =1,...,n	- коэффициенты системы, bi , i =1,..., m - сво-

бодные члены, xj , j =1,...,n - неизвестные.

Система может быть записана в матричном виде: A X = B ,

24

Лекция 3

a11

a12

...

a1n

где

A = (a

)

a

a

...

a

- основная матрица системы,

m,n

= 21

22

2n

ik

...

...

... ...

am1

am2

...

amn m,n

b1

B = (b )

b

- матрица-столбец свободных членов,

m,1

=

2

i

...

bm m,1

x1

X = (x

)

x

- матрица-столбец неизвестных.

n,1

=

2

k

...

xn n,1

Например, первое уравнение системы получено умножением первой строки матрицы A на столбец неизвестных: a11x1 + a12 x2 +... + a1n xn =b1 .

ОМатрица, полученная из матрицы A добавлением столбца свободных членов, называется расширенной матрицей системы:

a11

a12

...

a1n

b1

a

a

...

a

b

A = (A

B)=

21

22

2n

2

.

... ...

... ...

...

a

...

a

b

a

m1

m2

mn

m

m,n+1

О

Упорядоченное множество

из

n

величин

x1 = c1 ,

x2 = c2 , … xn = cn

называется решением СЛУ, если при подстановке этих чисел в систему уравнения превращаются в тождества. Решение может быть записано в виде матрицы

c1 X = (ck )n,1 = ... .

⎝cn n,1

ОСистема уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения.

ОСистема называется определенной, если она имеет единственное решение, и называется неопределенной, если она имеет бесконечное множество решений.

Системы линейных уравнений

25

ОСистема линейных уравнений (1) называется неоднородной, если матрица B не является нуль−матрицей , и называется однородной, если

B = .

!Однородная система всегда имеет нулевое (так называемое тривиальное) решение: x1 = x2 =... = xn = 0 .

Например,

1).	Система x1	+ x2	=1	несовместна, решений нет;
	x1	+ x2	= 2
2).	Система x1	+ x2	=1	совместна, но не определена, так как имеет беско-
	x1	+ x2	=1

нечное множество решений: x1 =1−c, x2 = c или (в матричной форме)

X= 1 −c , где c - произвольная постоянная;

c

3). Система x1	+ x2	=1	, совместна и определена, так как имеет единствен-
x1	− x2	=1
ное решение: x1 =1,			x2	= 0 (или X =	1	).
					0

3.2.Системы n линейных уравнений с n неизвестными. Матричный метод решения. Правило Крамера. Метод Гаусса (метод последовательного исключения переменных)

3.2.1.Системы n линейных уравнений с n неизвестными

ТСистема n линейных уравнений с n неизвестными имеет единственное решение, если определитель основной матрицы A отличен от нуля.

Доказательство:

Запишем систему уравнений в матричном виде: A X = B , где

a11	...	a1n	x1			b1
A = ...	...	... , X = (xi )n,1	= ... , B = (bk		)n,1	= ... .		(2)
a	...	a	x			b
n1		nn n,n	n	n,1		n	n,1
Пусть det A ≠ 0, тогда существует обратная матрица A−1 , A−1 A = E .
Умножим уравнение слева на A−1 :			A−1 A X = A−1B ,		X = A−1 B .

26

Лекция 3

С1. Если система n уравнений с n неизвестными имеет отличный от нуля определитель, она может быть решена матричным методом.

Например, система x1 + x2 =1 в матричном виде выглядит как

x1 − x2 =1

1	1	x		1
		1		= .
1	−1	x2		1

1

1

−2 ≠ 0 ,

A

−1

1

−1 −1

,

A =

, det A =

= −

2

1

−1

−1 1

x1

1 −1

−1 1

=

1

X =

= −

1

.

x2

2 −1

1

0

2. Если однородная система n уравнений с n

неизвестными имеет от-

личный от нуля определитель основной матрицы системы, то у нее существует только нулевое (тривиальное) решение.

Для однородной системы B = ; A X = . Так как существует A−1 , то

X=A−1 = .

3.2.2.Правило Крамера

Обозначим через ∆ - определитель основной матрицы системы (2) (главный определитель системы)

a11 ... a1n

∆ = det A = A = ... ... ... ,

an1 ... ann

∆i - i-й вспомогательный определитель системы (2), получается из ∆ заменой i -го столбца на столбец свободных членов,

a11

... a1,i−1

b1

a1,i+1

...

a1n

∆

i

=

A

=

a21

...

a2,i−1

b2

a2,i+1

...

a2n

.

i

... ... ... ... ... ... ...

an1

...

an,i−1

bn

an,i+1

...

ann

Системы линейных уравнений

27

ТЕсли главный определитель системы линейных уравнений не равен нулю, то система совместна и определена, причём единственное решение

(x1, x2 ,…, xn ) вычисляется по формулам Крамера:

x =

∆1 , x =

∆2 , … , x =

∆n .

1

∆

2

∆

n

∆

Доказательство:

1

−1

(V )

T

Матрица, обратная к матрице

коэффициентов: A

=

( A )

, ее

det A

V

1

i+ j

−1

q

=

(−1)i+ j

M ji

элементы A ij =

(−1)

M

ij

,

A

= (q ) ,

.

det

A

ij

ij

det A

Запишем элемент произведения X = A−1 B :

n

n

(−1)i+k

M

ki

1

n

i+k

xi = ∑qikbk = ∑

bk =

∑(−1)

bk Mki .

det A

k =1

k =1

det A k =1

По теореме о разложении определителя по столбцу сумма в круглых скобках – это определитель матрицы Ai , которая отличается от матрицы

A тем, что i-й столбец заменен на столбец свободных членов.

Таким образом, xi = ∆∆i .

Пример:

2x1 +3x2 + 2x3 = 9,

Решить систему: x1 + 2x2 +3x3 =14,

3x1 + 4x2 + x3 =16.

По формулам Крамера:

	2			3	2					9	3		2					2	9	2
∆ =	1			2	−3		= −6 ≠ 0, ∆1 =			14	2		−3	= −12,		∆2	=	1	14	−3	= −18,
	3			4	1					16	4		1					3	16	1
∆3 =			2	3	9		=12.
			1	2	14
			3	4	16
Вычислим значения неизвестных:
							x =	∆1	= 2 , x =			∆2	= 3		, x =	∆3	= −2 .
					1			∆	2			∆			3	∆

28

Лекция 3

3.2.3. Метод Гаусса (метод последовательного исключения неизвестных)

Рассмотрим систему n уравнений с n неизвестными (2). Данная система с помощью элементарных преобразований приводится к эквивалентной системе, решение которой находится проще.

Элементарными преобразованиями системы являются следующие:

перемена местами двух любых уравнений системы;

умножение любого уравнения системы на произвольное число k ≠ 0 ;

прибавление к одному уравнению системы другого уравнения, умноженного на произвольное число k ≠ 0 .

!1). Элементарным преобразованиям уравнений соответствуют элементарные преобразования строк расширенной матрицы системы A =(A B).

2). Элементарные преобразования матрицы не изменяют ее ранга. 3). Метод Гаусса справедлив и для произвольных систем ( m ×n ).

Метод Гаусса предполагает следующий алгоритм:

a

x +... + a

x

= b

11

1

1n

n

1

1. Для системы уравнений ..............................

a

x

+... + a

x

= b

n1 1

nn

n

n

записывают расширенную матрицу системы:

a11

a12

...

a1n

b1

a

a

...

a

b

A = (A

B)=

21

22

2n

2

... ...

... ...

... .

a

...

a

b

a

n1

n2

nn

n

n,n+1

2.Элементарными преобразованиями строк приводят ее к трапециевидной форме, при этом основная матрица системы приводится к верхнему тре-

угольному виду.

3.Возвращаясь к системе уравнений, определяют все неизвестные.

Пример:

x1 + x2 + x3 = 6

Решить систему 2x1 − x2 + x3 = 3 .

x1 + x2 − x3 = 0

Для удобства будем обозначать строки матрицы αi , а столбцы – β j .

Системы линейных уравнений

29

1 1

1

6

α2 − 2α1

1 1 1

6

2

−1

1

3

0 −3

−1

−9

, вернемся к системе урав-

α

−

α

1 1 −1

0

3

1

0 0

−2

−6

нений:

x

+ x

2

+ x

3

= 6

x

+ x

2

+ 3 = 6

1

1

− 3 = −9

− 3x2

− x3

= −9

− 3x2

− 2 x3

= −6

x3 = 3

x

+ 5 = 6

x

=1

1

1

x2 = 2

x2 = 2 .

= 3

= 3

x3

x3

!Употребляется также расширенный метод Гаусса, или метод Гаусса – Ньютона. В нем основная матрица системы элементарными преобразованиями строк преобразуется к диагональному виду, пункт 2 предыдущей схемы (так называемый прямой ход) дополняется обратным ходом

– преобразованием верхней треугольной матрицы к диагональной. Для предыдущего примера это будет выглядеть так:

1 1			1		6		1		1	1		6		1 1			0		3
	0	−3 −1			−9			0	−3 −1			−9			0	−3 0			−6
	0	0	−2		−6			0 0		1		3			0	0	1		3

1 1 0					3		1		0	0		1
	0	1	0		2			0 1		0		2		,
	0	0	1		3			0	0	1		3

откуда ответ очевиден.

3.3. Теорема Кронекера - Капелли

Рассмотрим систему m -линейных уравнений с n -неизвестными (1).

В начале лекции было показано, что ее можно представить в матричном виде. Будем рассматривать матрицу A размерности m ×n как набор строк αi (столб-

цовβj ):

30 Лекция 3

α

1

A =

α2

или

A = (β , β , ..., β ),

...

1

2

n

αm

a1 j

где α

= (a

,a

,...,a ) – матрица - строка; β

a

- матрица-столбец.

i

j

=

2 j

i1

i2

in

a

mj

Введем понятие линейной зависимости строк (столбцов) матрицы.

О Линейной комбинацией строк называется выражение вида:

k

λα1 1 + λ2α2 + ... + λkαk = ∑λαi i =

i=1

=λ1 (a11 a12 ... a1n )+λ2 (a21 a22 ... a2n )+ ... + λk (ak1 ak 2 ... akn ).

ОСтроки матрицы α1, α2 , ..., αk называют линейно зависимыми, если существует такой набор чисел λ1, λ2 , ..., λk , не равных одновременно нулю, при которых линейная комбинация строк обращается в ноль:

λ1α1 + λ2α2 + ... + λkαk = 0 .

ТСтроки матрицы являются линейно зависимыми, если одна из них является линейной комбинацией остальных:

αk = λα1 1 + λ2α2 + ... + λk −1αk −1 +λk +1αk +1 + ... + λnαn .

!Действиям над строками матрицы соответствуют действия над уравнениями системы.

ОПусть матрица A размерности (m×n) имеет ранг r . Отличный от нуля минор порядка r , составленный из элементов матрицы A , называется

базисным минором матрицы A .

ОНеизвестные, коэффициенты перед которыми входят в базисный минор, называются базисными неизвестными. Неизвестные, не являющиеся базисными, называются свободными.

ТТеорема о базисном миноре. Если матрица (m×n) имеет ранг r , то существуют r таких строк (столбцов), что все остальные строки (столбцы) являются линейными комбинациями данных. Из элементов, входящих в эти строки (столбцы), можно построить базисный минор матрицы.

!Базисных миноров может быть много, но ранг определяется одно-

Системы линейных уравнений

31

значно.

С1). Строки (столбцы), входящие в базисный минор, линейно независимы.

2). Все строки (столбцы) матрицы, не входящие в базисный минор, линейно зависимы с базисными.

3). Число линейно независимых строк матрицы равно числу линейно независимых столбцов и равно рангу r .

4). rang (A)≤ min (m,n).

ТТеорема Кронекера - Капелли. Для того чтобы система m уравнений с

n неизвестными была совместной, необходимо и достаточно, чтобы ранг основной матрицы системы равнялся рангу расширенной матрицы:

r(Α) = r (Α Β).

Доказательство*:

Достаточность. Пусть r(Α) = r(ΑΒ). Рассмотрим столбцы матрицы A и A :

a

a

b

11

1n

1

β

1

= a21

, … ,

β

n

= a2n

,

B =

.

am1

amn

bm

Так как добавление столбца

B в множество {β1 ,..., βn } не увеличивает количество

линейно независимых столбцов, столбец B есть линейная комбинация столбцов ос-

новной матрицы, т.е. существуют такие x1, x2 ,…, xn ≠ 0 , что

B = x1β1 + x2β2 +…+ xn βn ,

или

b

a

a

a

1

= x

11

+ x

2

12

+... + x

n

1n

.

1

b

a

m1

a

m2

a

m

mn

b

= a

x +... + a

x

Записывая последнее в виде

1

11

1

1n

n

,

b

= a

m1

x +... + a

mn

x

n

m

1

убеждаемся в том, что x1, x2 ,…, xn - решение системы, система совместна. Необходимость. Пусть система совместна, x1, x2 ,…, xn - решение системы. Записывая систему в виде

a

a

a

b

11

x

+

12

x

2

+... +

1n

x

n

=

1

,

1

a

m1

a

m2

a

b

mn

m

x1β1 + x2β2 +…+ xn βn = B ,

32 Лекция 3

видим, чтоB является линейной комбинацией β1,..., βn , добавление столбца свободных членов не увеличивает ранга матрицы, r( A) = r( A) .

	Итак, если r(Α) ≠ r (Α				Β), то система заведомо не имеет решений; если же
r(Α) = r (Α			Β), то возможны два случая:
1)	если r = n , тогда решение единственно;
2)	если r < n , тогда решений бесконечно много.

3.4. Однородные системы линейных уравнений

Однородная система имеет вид:

a x	+ a x +... + a x = 0,
11 1	12 2	1n n
a21x1 + a22 x2 +... + a2n xn = 0,
............................................
a x	+ a x	+... + a x = 0,
m1 1	m2 2	mn n

ей соответствует матричное уравнение Α Χ = .

Однородная система всегда совместна, так как r( A) = r( A) , поскольку

нулевой столбец не меняет ранг матрицы, всегда существует нулевое реше-

ние (0, 0, ..., 0) .

ТДля того чтобы однородная система имела ненулевое решение, необходимо и достаточно, чтобы r( A) < n .

Доказательство:

1)r не может быть больше n (ранг матрицы не превышает числа столбцов или строк);

2)r ≠ n , т.к. если r = n , то главный определитель системы ∆ ≠ 0 , и, по

формулам Крамера, существует единственное тривиальное решение x1 = x2 =... = xn = 0 , что противоречит условию. Значит, r( A) < n .

СДля того чтобы однородная система n линейных уравнений с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы

∆= 0 .

Системы линейных уравнений

33

3.5.Схема отыскания общего решения системы m уравнений с n неизвестными

1. Находим ранги матриц A и (A B).

Если r(Α) ≠ r (Α Β ), то система не имеет решений.

Если r(Α) = r (Α Β )= r , то у системы есть решения. У матриц A и (A B) есть общий базисный минор. Выбираем его.

2.Оставляем в системе только те уравнения, коэффициенты которых входят в общий базисный минор. Остальные уравнения являются линейными комбинациями этих уравнений и не несут дополнительной информации.

3.Сравниваем ранг и количество неизвестных.

Если r = n , то есть порядок базисного минора совпадает с количеством неизвестных, решаем систему n уравнений с n неизвестными (ее определитель ∆ ≠ 0) и получаем единственное решение.

Если	r < n ,	то в системе имеются (n − r)	свободных неизвестных. Тогда
x1 ,	x2 , ...,	xr – базисные неизвестные, а	xr+1 , ..., xn – свободные неиз-

вестные.

Переносим свободные неизвестные в правую часть уравнений системы:

a x + a x +... + a x = b − a x							−... − a x ,
11 1	12 2	1r r	1	1,r+1 r		+1		1n n
a21x1 + a22 x2 +... + a2r xr = b2 − a2,r+1xr+1 −... − a2n xn										,	(3)
...........................................................................
a x + a x +... + a x = b − a x								−... − a	x .
r1 1	r 2 2	rr r	n		r,r+1	r+1			rn n
или, в матричной форме,
	AX r	= B0 + xr+1B1 + xr+2 B2 +...						+ xn Bn−r ,			(4)
где
		a	a	...	a
		11	12		1r
	A = a21		a22	...	a2r		, det A ≠ 0 ,
				... ...
		... ...
		ar1	ar 2	...	arr

		x1
X		x		,
	r	= 2
		...
		xr

	b1
B	b		,
	= 2
0
	...
	br

	a1,r+1				a1,n
	a		, ...,		a
B = − 2,r+1				B = −		2,n .
1	...			n−r		...
	a				a
	r,r+1						r,n

34

Лекция 3

Система (3) является следствием исходной системы (1) и ее решение может быть найдено любым ранее рассмотренным способом.

Пусть свободные неизвестные принимают значения
xr+1 = c1 ,		xr+2 = c2 ,		...,			xn = cn−r .
Тогда система (4) принимает вид:
AX r	= B0 + c1B1 + c2 B2 +... + cn−r Bn−r							(5)
и базисные неизвестные x1, x2 ,			..., xr	выражаются определенным образом
через эти значения: xi = xi (c1 ,		c2 , ...,		cn−r ) ,			i =1,2,..., r .	Решение неодно-
родной системы A X = B можно записать в виде матрицы-столбца:
	x1(c1, c2 , ..., cn−r )
	x (c , c , ..., c				)
	2	1	2	n−r
	...........................
X =	xr (c1, c2 , ..., cn−r )					.		(6)
			c1
			c2
			...
			cn−r

Поскольку свободные неизвестные могут принимать произвольные числовые значения, то исходная система имеет бесконечно много решений. Выражение (6) называется общим решением системы (1). Если константам c1, c2 , ..., cn−r придать конкретные значения, то получим частное решение

системы (1).

Пример:

	2x		+3x	2	− x		3	= 2,
		1
Решить систему: 7x1 + 4x2 + 2x3 = 8,
			−2x2 + 4x3							= 5.
	3x1
Рассмотрим расширенную матрицу:
			2 3 −1						2						−1 3 2			2
			7 4 2						8				~		2 4 7			8		~
(Α	Β )=									~	β3	↔ β1
			3 −2 4						5						4 −2 3			5
			α2 + 2α1								−1	3	2		2
											0	10	1112
			~ α			+ 4α				~						.
					3			1			0	0	0		1

Системы линейных уравнений	35
Следовательно, r(Α) = 2	и r(Α		Β) = 3 . Поскольку r(Α) ≠ r(Α		Β) , система

несовместна. Очевидно, что третье уравнение преобразованной системы: 0 x1 +0 x2 +0 x3 =1 не имеет решений.

Пример:

			x1 − x2 + x3										=12,
		2x1 +3x2 − x3											=13,
Решить систему				3x2 + 4x3									= 5,
	−3x			+ x	2	+ 4x						3	= −20.
			1
Рассмотрим расширенную матрицу:
		1 −1 1							12																		1 −1 1							12
		2 3 −1							13							α					−2α						0 5 3						−11
(Α	Β) =														~		2						1		~												~
		0 3 4							5							α					+3α						0 3 4						5
																	4						1
																											0 −2 7						16
	−3 1 4								−20
			1	−1			1				12																	1	−1	1					12
			0 3 4								5					α2 −α3
																												0 −2 7
~ α2 +α4 ~			0 3 4								5				~	α					↔		α			~									16	~
																		4						2				0	3	4					5
			0	−2			7				16
							1 −1 1													12						1		−1 1			12
	~ 2α3 +		3α2 ~				0 −2 7													16			~			0 −2 7					16
							0 0 29													58						0 0 1					2

Следовательно, r(Α) = r(ΑΒ) = 3 , поэтому система совместна и имеет единственное решение.

x − x		+ x	=12,
	1 2	3
Преобразованная система имеет вид:	− 2x2 + 7x3 =16,
		x3	= 2,

ее решение: x1 =9, x2 = −1, x3 = 2 .

36

Лекция 3

Пример:

x −4x

2

+ 2x

3

= −1,

1

Решить систему

2x1 −3x2 − x3 −5x4

= −7,

3x1 −7x2 + x3 −5x4 = −8.

Рассмотрим расширенную матрицу:

1 −4 2 0

−1

α2

−2α1

1

−4 2 0

−1

2

−3 −1 −5

−7

~

0 5 −5 −5

−5

~

(Α

Β) =

~ α

−

3α

3

3

−7 1 −5

−8

1

0 5 −5 −5

−5

1 −4 2 0

−1

1 0 −2 −4

−5

~ α

3

−α

2

~

0 1 −1 −1

−1

~

α

+ 4α

2

~

0 1 −1 −1

−1

.

1

0 0 0 0

0

0 0 0 0

0

Следовательно, r(Α) = r(ΑΒ) = 2 , поэтому система совместна и не определена. Выберем x1 и x2 в качестве базисных неизвестных и запишем преобразованную систему:

x1 = −5 + 2x3 + 4x4 ,x2 = −1 + x3 + x4 .

Полагая x3 =c1 , x4 = c2 ,				где c1 и c2			− произвольные числа, получаем об-
щее решение системы
	x1		−5 + 2c1 + 4c2						−5				2		4
X	x			−1	+ c	+ c				−1		+ c	1	+ c		1
	= 2		=		1	2			=							0	.
	x				c					0		1	1	2
	3				1					0						1
	x4				c2								0

Решение соответствующей однородной системы

x	− 4x	+ 2x				= 0,
1	2				3
2x1 − 3x2 − x3 − 5x4 = 0,
			+ x3 − 5x4 = 0
3x1 − 7x2
можно записать в виде:
			2				4
			1					1
X = c					+ c				.
	1		1			2		0
			0					1

Системы линейных уравнений	37
3.6*. Фундаментальная система решений

Т Если СЛУ имеет вид A X = c1B1 + c2 B2 , то ее решение может быть записано в виде

X = c1 X1 +c2 X2 , где X1 и X 2 - решения систем A X = B1 и A X = B2 соответственно.

Доказательство:

X1 = A−1 B1 , X2 = A−1 B2 ,

X = A−1 (c1 B1 + c2 B2 )= A−1 (c1 B1 )+ A−1 (c2 B2 )=

=c1 A−1 B1 +c2 A−1 B2 = c1 X1 +c2 X2.

Впредыдущем параграфе возникла система (5)

AXr = B0 +c1B1 +c2 B2 +... +cn−r Bn−r .

Из только что доказанной теоремы следует, что

Xr = X

где Xr,0 , Xr,1, Xr,2 , ...,

правой части столбцов

r ,0 +c1 Xr ,1 +c2 Xr,2 +... +cn−r Xr ,n−r ,

(7)

Xr,n−r - решения системы (5) при подстановке в нее (5) вместо

B0 , B1, B2 , ..., Bn−r .

x1

Поскольку Xr = x...2 , это означает, что базисные неизвестные линейно зависят от

xr

свободных неизвестных и в выражении

x1 (c1, c2 , ..., cn−r )
x (c , c , ..., c			)
2	1 2	n−r
...........................
	(c1, c2 , ..., cn−r )
xr					(8)
X =	c1
	c2
	...
	cn−r
для общего решения системы	xi = xi (c1, c2 , ..., cn−r )				- линейные функции
c1, c2 , ..., cn−r .

Это позволяет записать матрицу–столбец (6) - общее решение системы (1) в виде:

X = X0 +c1 X1 +c2 X2 +...+cn−r Xn−r ,

(9)

38	Лекция 3
где частные решения Xi	(i = 0, 1, 2, ..., n −r) , образующие фундаментальную сис-

тему решений, получены при следующих значениях постоянных в выражении (5):

		x1 (0, 0, ..., 0)					x1 (1, 0, ..., 0)					x1 (0, 1, ..., 0)					x1 (0, 0, ..., 1)
		x (0, 0, ..., 0)					x (1, 0, ..., 0)					x (0, 1, ..., 0)					x (0, 0, ..., 1)
		2					2					2					2
		....................					....................					....................					...................
X		= xr	(0, 0, ..., 0)		, X		= xr	(1, 0, ..., 0)		, X		= xr	(0, 1, ..., 0)		, ..., X		= xr	(0, 0, ..., 1)	.
	0		0			1		1			2		0			n−r		0
			0					0					1					0
			...					...					...					...
			0					0					0					1

Выражение (8) называется разложением по фундаментальной системе решений.

В результате изучения материала, изложенного в этой лекции, студент должен знать:

основные понятия теории СЛУ (основная и расширенная матрицы системы, совместные / несовместные, определенные/неопределенные однородные/неоднородные системы, базисные и свободные неизвестные, общее и частное решение СЛУ);

способ выяснения, имеет ли система решения (теорема Кронекера – Капелли);

методы решения СЛУ – матричный, правило Крамера, метод Гаусса;

схему отыскания общего решения СЛУ.

Студент должен понимать, что преобразования строк матриц системы соответствуют преобразованиям уравнений системы.

Лекция 4 ВЕКТОРНАЯ АЛГЕБРА

В лекции 4 излагаются элементы векторной алгебры. Необходимость применения векторного исчисления при изложении технических дисциплин вызвана не столько удобством и наглядностью математических формулировок законов, сколько объективными свойствами изучаемых явлений. Направленные величины используются при описании широкого круга явлений, относящихся к теоретической механике, механике жидкости и газа, теории электромагнетизма. Курс математики для инженерных специальностей включает также элементы векторного анализа, который будет излагаться после изучения дифференциального и интегрального исчислений одного и нескольких переменных.

4.1.Основные определения

4.2.Линейные операции над векторами 4.3.* Линейная зависимость векторов.

Геометрические критерии линейной зависимости.

4.4.Базис и координаты

4.5.Ортонормированный базис. Декартова прямоугольная система координат

4.6.Скалярное произведение векторов. Определение. Алгебраические свойства. Геометрические приложения. Выражение через декартовы координаты сомножителей

4.7.Векторное произведение векторов. Определение. Алгебраические и геометрические свойства. Выражение через декартовы координаты сомножителей

4.8.Смешанное произведение векторов. Определение. Алгебраические и геометрические свойства. Выражение через декартовы координаты сомножителей

4.1.Основные определения

Величины, для определения которых достаточно знать одно число, называются скалярами (температура, масса, работа силы, плотность). Величины другого рода характеризуются не только численным значением, но и направлением в пространстве. Таковы перемещение, скорость, ускорение, сила, напряженность электрического поля и т.д. Рассмотрение такого рода величин приводит к понятию вектора.

ОГеометрическим вектором (вектором) назы-

вается направленный отрезок (отрезок, у которого одна граничная точка считается начальной, другая – конечной).

закрепленного вектора.

40						Лекция 4
		На чертеже вектор обозначается стрелкой; над буквенным обозначением
				JJG
		вектора также ставится стрелка AB , a .
	О	Длиной вектора (модулем) называется расстояние между началом и кон-
			JJG
		цом вектора. Обозначение:	AB	или	a	.

ОНулевымG векторомG называется вектор, у которого начало и конец совпадают: 0 , 0 = 0 .

ОВекторы называются коллинеарными, если лежат на одной прямой, либо на параллельных прямых.

Нулевой вектор коллинеарен любому вектору.

ОТри вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов, то эти векторы компланарны.

!Вектор, фигурирующий в определении, носит название связанного, или

JJJG

Если же точка приложения вектора (точка A для вектора AB ) может быть выбрана произвольно, вектор называется свободным. Если точка приложения может двигаться по линии действия вектораG , говорят о

скользящем векторе. Иначе говоря, свободный вектор a является представителем бесконечного множества связанных или скользящих векторов.

В дальнейшем мы будем рассматривать только свободные векторы. Для них, в частности, справедливо следующее определение.

ОДва вектора равны, если они коллинеарны, име-

ют одинаковуюG Gдлину и направление. Например, a =b .

4.2. Линейные операции над векторами

ОСуммой aG +b двух векторов a и b называется

векторG, идущий из начала вектора a в конец вектора b при условии, что начало вектора b приложено к концу вектора a (правило треуголь-

ника).

Векторная алгебра

41

Свойства операции сложения векторов:

G

G

G

G

1˚.

a +b

=b

+ a

(переместительное свойство).

2˚.

G

G

G

G

G

G

(сочетательное свойст-

(a +b )+ c

= a +(b + c )

во).

3˚.

Существует

нулевой

вектор

0 ,

такой,

что

G

G

G

a +

0

= a

для любого вектора

a (особая роль

нулевого вектора).

aG существует противо-

4˚.

Для каждого вектора

положный

ему

′

G

такой,

что

G

вектор a =

−a ,

G

G

=

a +

(−a )

0 .

Свойства доказываются геометрически. Докажем, например, свойство 1˚.

Рассмотрим

произвольный

параллелограмм

ABCD . Пусть

G

JJG

G

a = AB ,

JJJG

G

G

JJJG

JJJG

JJJG

JJG

JJJG

JJG

JJJG JJJG

G

G

b = BC . Тогда a

+b = AC . Но BC

= AD , DC =

AB

AC

= AD + DC

= b

+ a .

G

G

G

Таким образом, a

+b =b

+ a .

!При доказательстве свойства 1˚ обосновано еще одно правило сложения векторов, назы-

ваемое правиломG параллелограмма: если векторы aG и b приложены к общему началу и

на

них построен параллелограмм, то сумма

G

G

a +b этих векторов представляет собой диа-

гональ параллелограмма, идущую из общего

G

G

начала векторов a и b .

G

G

G

G

!

Вычитание векторов определяется через сложение: a

−b = a

+ (−b) .

Иначе: если векторы

aG и b приложены к общему началу,

то разностью

G

G

G

G

векторов a

и b будет вектор a −b , идущий из конца вектора b к концу

вектора aG.

Произведением αaG

вектора a на вещественное число α

называется

О

вектор bG,

коллинеарный вектору a , имеющий длину

α

aG

и на-

правление,

совпадающее с направлением вектора a

в случае α > 0 и

противоположное направлению вектора a в случае α < 0 . Геометрический смысл операции умножения вектора на число:

при умножении вектора aG на число α вектор a «растягивается» в α раз

при

α

>1, при 0 <

α

<1 вектор «сжимается» в

1

раз. Если α < 0 , век-

α

тор, кроме этого, меняет направление на противоположное.

42								Лекция 4
Свойства операции умножения вектора на число:
5˚.	G	G		G	G	(распределительное свойство относительно суммы
	α(a	+b )	=αa +αb
	векторов).
6˚.	(α + β )aG		=αaG + βaG			(распределительное свойство относительно суммы
	чисел).
7˚.	α(βaG)= (αβ )aG				(сочетательное свойство чи-
	словых сомножителей).
8˚.	1 aG = aG (существование единицы).
	ДокажемG		,G	например, свойство 5˚. Отложим
векторы a и			b	от общего начала и построим на
них параллелограмм, диагональ которого будет
представлять собой сумму aG							+b . При «растяжении» (α >1 ) сторон этого па-
раллелограмма в α					раз его диагональ также «растягивается» в α раз, но это и
					G	G	G
означает, что сумма αa +αb							равна α(a +b) .

!Свойства 1˚ ÷ 7˚ для векторов позволяют производить выкладки в векторной алгебре по тем же правилам, по которым производятся аналогичные выкладки в алгебре вещественных чисел.

4.3.* Линейная зависимость векторов. Геометрические критерии линейной зависимости

ОЛинейной комбинацией векторов a1 , aG2 , ..., aGn называют выражение:

G

G

G

n

G

α1a1 + α2a2

+ ...+αnan =

∑αi ai ,

i =1

где α , α

2

, ..., α

n

- произвольные действительные числа.

1

G

G

G

О

называется линейно зависимой, если существуют

Система векторов a1

, a2

, ..., an

действительные числа α1 , α2 , ..., αn , такие, что хотя бы одно из них отлично от нуля,

и выполняется равенство:

+ α aG

+ ...+α aG = 0 .

α aG

(*)

1 1

2 2

n n

В противном случае, т.е. если линейная комбинация (*) обращается в ноль только при всех αi = 0, i =1, ..., n , то система векторов называется линейно незави-

!симой.

Если векторы линейно зависимы, то любой вектор может быть выражен в виде линейной комбинации остальных. Например, если αn ≠ 0 , то из (*) следует, что

G

G

G

G

n−1

G

, где

β1 = −

α1

, ..., βn−1

= −

αn−1

.

an = β1a1

+ β2 a2

+ ...+βn−1an−1

= ∑βi ai

αn

αn

i=1

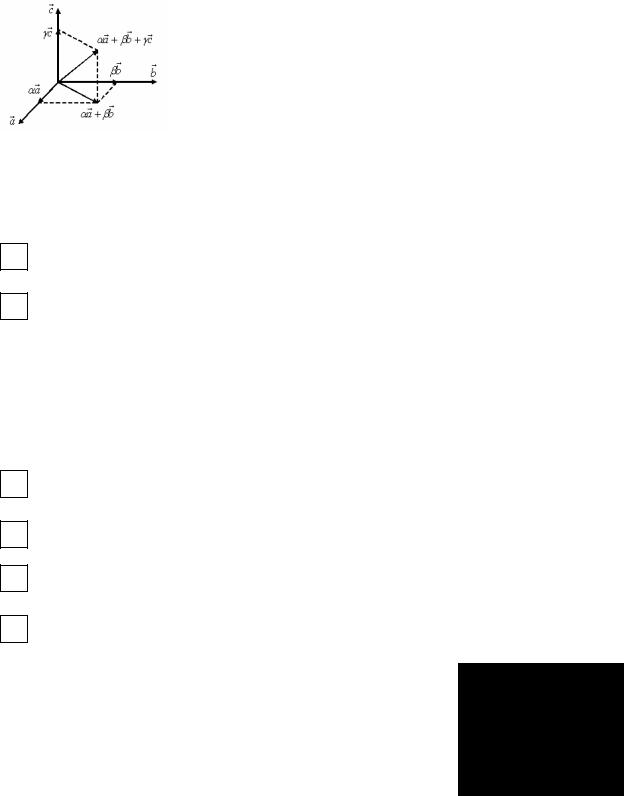
Векторная алгебра

43

Геометрические критерии линейной зависимости

ТСистема двух ненулевых векторов a1 , aG2 линейно зависима тогда, и только тогда, когда векторы коллинеарны.

Доказательство:

Необходимость. Пусть α aG

+ α

aG

= 0 и α ≠ 0 . Тогда α aG

= −α

aG

,

aG

= −α2 aG

; или

1 1

2 2

1

1 1

2 2

1

α

2

aG

= λaG , где λ = −α2 .

1

1

2

α1

Достаточность.

G

G

. Запишем

это равенство

в виде

G

G

G

или

Пусть

a

= λa

a

−λa

= 0

G

G

G

1

2

1

2

+ α

где α =1,

α

= −λ ≠ 0 . Итак, существует нулевая линейная комби-

α a

a

2

= 0 ,

2

1

1

2

1

нация с ненулевыми коэффициентами, а это и означает, что система векторов линейно зависима.

ТСистема трех векторов aG1, aG2 , aG3 линейно зависима тогда и только тогда, когда векторы компланарны.

ТСистема четырех векторов всегда линейно зависима, т.е. для любых aG1, aG2 , aG3 , aG4

найдутся

G

такие

числа

α , α

, α

, α

, не равные одновременно нулю, что

G

+ α

G

+α

G

G

1

2

3

4

α a

a

+α a

a

4

= 0 .

1

1

2

2

3

3

4

4.4. Базис и координаты

ОБазисом в пространстве будем называть три некомпланарных вектора, взятые в определенном порядке.

ОБазисом на плоскости будем называть два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.

ОБазисом на прямой будем называть любой ненулевой вектор этой прямой.

Т Каждый вектор может быть разложен по базису в пространстве и это разложение единственноG G .G

Иначе, если a , b , c – три некомпланарныхG вектора в пространстве, то любой вектор

d

может

G

быть

записан

в

виде:

G

G

G

d

=αa

+ βb +γc .

Доказательство возможности:

G G

G

Пусть {a, b,

c } - некоторый базис в простран-

стве, dG - произвольный вектор.

Тогда

αaG + βb +γcG = 0G

только при

α = β = γ = 0

. α aG

+α

bG

+α

cG

+α

dG = 0 , при этом α4 ≠ 0 ,

так как если

1

2

3

4

44

Лекция 4

α4 = 0 , то α1aG +α2bG +α3cG = 0 , а этого быть не может, т.к. {aG, bG, cG} - ба-

зис.

Тогда

G

G

G

G

G

α1

G

α2 G

α3

G

G

G

G

α

4

d

= −α a −α

b −α

c

, d = −

a −

b −

c , d

=αa + βb

+γc .

1

2

3

α4

α4

α4

Доказательство единственности:

Предположим, что существуют два разложения вектора dG

по базису

G G

G

}, то есть

G

G

G

G

G

G

G

{a, b,

c

d =

α1a

+ β1b +γ1c ;

d =α2a +

β2b +γ2c . Вычтем из од-

ного равенства

другое: (α1 −α

G

+ (

G

G

.

Так как

2 )a

β1 − β2 )b + (γ1 −γ2 )c =

0

G G

G

}- базис, ни один из векторов

G

G

{a, b, c

{a, b,

c } не может быть выражен

через

другие

при

ненулевых

коэффициентах,

поэтому

α1 =α2 ,

β1 = β2 ,γ1 =γ2 .

dG представляет собой пространственную диаго-

!

Геометрически вектор

наль параллелепипеда, построенного на векторах a ,

b и сG.

ОКоэффициенты разложения вектора по базису называются координатами вектора в данном базисе и в каждом базисе определяются одно-

значно:	G	G	G	G
	d	=αa	+ βb	+γc ={α, β,γ }.

ТПри сложении двух векторов d1 и d2 их координаты (Gотносительно любого базиса) складываются. При умножении вектора d1 на любое число

α все его координаты умножаются на это число.

Доказательство:

G

G

G

G

G

G

G

d

=α

+ β

+γ

. Тогда в силу свойств 1˚-7˚

Пусть d

=α a

+ β b +γ c ,

2

a

2

b

2

c

1

1

1

1

2

линейных операций над векторами

dG

+ dG

= (α +α )aG + (β + β )bG + (γ +γ )cG,

λdG1 = (λα1 )aG + (λβ1 )bG + (λγ1 )cG.

Всилу единственности разложения вектора по базису теорема доказана.

ОСистемойG координат в пространстве называют совокупность базиса {aG, b, cG} и некоторой точки, называемой началом координат.

JJJJG

ОВектор OM , идущий из начала координат в точку M , называется ради-1 2 1 2 1 21 2

	ус-вектором точки M .	JJJG
О	Координатами точки M (α, β,γ ) называются координаты вектора OM .
	JJJG
	Таким образом, координаты радиус-вектора OM	и координаты точки

M совпадают.

Векторная алгебра

45

4.5.Ортонормированный базис. Декартова прямоугольная система координат

Пусть в качестве базиса выбраны три взаимно перпендикулярных векто-

ра с длинами, равными единице.
G G	G		G		G
Обозначения: {i, j,k},	i	=	j	=	k	=1

ОТакой базис называетсG G Gя ортонормированным (ОНБ). Векторы i , j, k называются базисны-

ми ортами. Зафиксируем точку О – началоG координат и отложим от нее векторы i , j, k . По-

лученная система координат называется пря-

моугольной декартовой. Координаты любого вектора в этом базисе называются декартовыми координатами вектора:

aG ={x, y, z} = x iG+ y Gj + z k

	Z
	z		M
	G
	k	Gj	Y
	x i 0
			y

X

ОПрямые линии, проведенные через начало координат по направлениямG

i– порождаетбазисных векторов, называются координатными осями:

G G

Ox ; j – порождает Oy ; k – порождает Oz . Координаты точки М (вектора

JJJJG

OM ) в декартовой системе координат по осям Ox , Oy , Oz называются

соответственно абсциссой, ординатой и аппликатой.

Декартовы прямоугольные координаты x, y, z вектора a равны проекциям этого вектора на оси Ox , Oy , Oz соответственно; другими словами,

x = npOX aG =

aG

cosα , y = npOY a =

aG

cos β , z = npOZ aG =

aG

cosγ .

Здесь α, β, γ

–

углы, которые составляет вектор a с координатными

осями Ox , Oy , Oz соответственно, при этом cosα , cos β , cosγ

называ-

ются направляющими косинусами вектора a .

G

Вектор aG0 =

aG

={cosα, cos β, cosγ} представляет собой вектор единич-

a

ной длины данного направления, или орт данного направления. Для направляющих косинусов справедливо соотношение:

cos2 α + cos2 β + cos2 γ =1.

46

Лекция 4

4.6.Скалярное произведение векторов. Определение. Алгебраические свойства. Геометрические приложения. Выражение через декартовы координаты сомножителей

G

G

О

n

Углом между векторами

a и b (обозначается (a , b )) называется наи-

меньший угол,

на который надо повернуть векторa до совмещения с

вектором bG.

О

Проекцией вектора aG

на ось l,

прl a , называ-

ется величина А`В` направленного отрезка

JJJJJG

A`B` оси l.

(

G

)

G

G

G

G

n

l0

прl a =

a

cosϕ =

a

cos

a , l0

, где

- орт

оси l.

О

Скалярным произведением двух векторов называется число, равное

произведению длин этих векторов на косинус угла между ними:

G G

G

G

G

G

G

G

G G

(a b )= (a,b )

= a b =

a

b

n

cos(a , b ).

!Если один из векторов aG, b нулевой, то (aG b )= 0 .

Алгебраические свойства скалярного произведения:

1˚.	Переместительное свойство:				G	G	G
					(a b )=(b		a).
2˚.	Сочетательное свойство:				G		G	G	G	G
					(λa	b )= λ(a		b )=(a		λb )
3˚.	Распределительное свойство:				((aG +b ) cG)= (aG cG)+(bG cG),
					(aG (b + cG))= (aG bG)+(aG cG).
4˚.	G G	G	G	G			G
	(a, a)> 0 , если	a	≠ 0 , и (a,	a)= 0		, если a = 0 .

!Доказательства свойств следуют из определения.

Геометрические приложения скалярного произведения:

1.Связь с понятием модуля:

G G

G G

G G

=

G

2

cos0

o

=

G

2

;

G

=

G G

(a,a)=| a | | a | cos a , a

a

a

a

(a, a ).

G		(aG, b )
G
n
2. Косинус угла между векторами: cos(a , b )=		aG				bG		.

3.Связь с понятием проекции.

Векторная алгебра

47

Проекция прGaG

вектора

aG на вектор b :

b

G

G

G

G

G

G

G

G

G

G

(a, b )

(a, b )

G (a, b )

n

прbGa =

a

cos(a , b )=

a

aG

bG

=

bG

, т.е. прbGa =

bG

.

G

G

Аналогично: прaGbG =

(a,Gb ).

a

4.Необходимым и достаточным условием ортогональности (перпендикулярности) двух ненулевых векторов является равенство нулю их скаляр-

G	G G G	π	G G
	n
ного произведения: a b : (a , b )= 2			(a,b) = 0 .

Выражение скалярного произведения векторов через декартовы координаты сомножителей

ТЕсли два вектора aG и bG заданы своими декартовыми прямоугольными

координатами a ={x1, y1, z1}, b ={x2 , y2 , z2}, то скалярное произведе-

ние этих векторов равноG сумме парных произведений их соответствующих координат, т.е. (aG, b )= x1x2 + y1 y2 + z1z2 .

Доказательство: aG = x1iG + y1 Gj + z1k , b = x2i + y2 Gj + z2kG. В силу свойств 2 и 3 имеем:

(aG, bG)=((x1iG + y1 Gj + z1kG),(x2iG + y2 Gj + z2kG))= = x1x2 (iG,iG)+ x1 y2 (iG, Gj )+ x1z2 (iG,k )+

+y1x2 (Gj,iG)+ y1 y2 (Gj, Gj )+ y1z2 (Gj,k )+

+z1x2 (kG,iG)+ z1 y2 (kG, Gj )+ z1z2 (kG,kG).

G

G

G

G

G

,

Так как i

j

, i k ,

j k

Gj) =1 1 cos90o = 0 .

то (iG, Gj) = (iG, kG) = ( Gj,iG) = ( Gj, kG) = (kG,iG) = (kG,

G G

G

2

G G

G

2

G

G

Но (i ,i ) =| i

|

cos(i ,i ) =| i

|

=1, аналогично ( j, j) =1, (k , k ) =1.

G G

Таким образом, (a, b )= x1x2 + y1 y2 + z1z2 .

1. Длина вектора: aG ={x,

y, z},

aG

= (aG, aG) =

С

x2 + y2 + z2 .

2. Расстояние между двумя точками:

Если A=(x1, y1, z1 ), B =(x2 ,

y2, z2 )

– точки,

48 Лекция 4

то ρ(AB) =

JJJG

= (x

−x )2 +(y − y )2

+(z −z )2 .

AB

1

2

1

2

1

2

3. Угол между векторами:

Если aG

= (x1, y1, z1 ), bG = (x2 ,

y2 ,

z2 ), то

G

G

(aG, b )

x x

+

y y

+

z z

, b )=

aG bG

=

+ z22 .

cos(a

x12 + y12

+ z12

2

x22 + y22

n

1

2

1

1

2

4. Проекция прGaG

вектора a на вектор b

b

G

(aG, b )

x1x2 + y1 y2 + z1z2

прbGa

=

G

=

.

x22 + y22 + z22

b

5. Направляющие косинусы вектора:

G

G

x

cosα

= cos a,

i

=

x2

+ y2

+ z2

G

G

y

cos β

= cos a,

j

=

x2

+ y2

+ z2

G

G

z

cosγ

= cos a,

k

=

x2

+ y2

+ z2

cos2 α + cos2 β + cos2 γ = 1

,

,

;

4.7.Векторное произведение векторов. Определение. Алгебраические свойства. Геометрические приложения. Выражение через декартовы координаты сомножителей

ОУпорядоченная тройка некомпланарных векторов a1 , aG2 , aG3 , приведен-

ныхGк одному началу, называется правой, если из конца третьегоG вектора a3 кратчайший поворот первого вектора a1 ко второму a2 виден совершаемым против часовой стрелки. В противном случае тройка назы-

вается левой.		JG
JJG
a3	JJG	a3	JJG
	a2
			a2
	JG	G
	a1	a1
	правая	левая

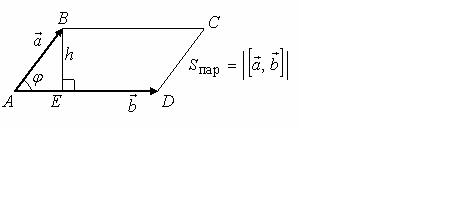
Векторная алгебра

49

Система координат называется правой, если ее базисные векторы обра-

О

зуют правую тройку.

В дальнейшем мы будем рассматривать только правые системы коорди-

нат.

При перестановке местами двух соседних векторов ориентация тройки

меняется.

Если тройки

G

b c a ,

c a b

-

правые, то

G G G

G

a b c ,

a c b ,

c b a ,

G

G G

b

a c - левые. При круговой (циклической) перестановке векторов ори-

ентация тройки не меняется.

Векторным произведением вектора

a на вектор b называется вектор

О

G

G G

G

G

G

G

c

= a, b

= a

×b

= a

×b , удовлетворяющий следующим трем требова-

ниям:

G

G

G

1). Длина вектора c равна произведению длин векторов a

и b на синус

G

G

G

G

G

JGG

угла между ними, т.е.

c

=

=

a

b

sin (a,b).

a, b

G

G

2). Вектор c ортогонален к каждому из векторов a и b , т.е. c перпендикулярен плоскостиG , в которой лежат векторы a и b .

3). Вектор c направлен так, что тройка a b c является правой.

Алгебраические свойства векторного произведения:

1˚. Антиперестановочность сомножителей:

2˚. Сочетательное свойство:

3˚. Распределительное свойство: 4˚. [aG, aG]= 0G для любого вектора a .

aG, bαaG, baG + b,

= − bG, aG .=α aG, bG .

cG =[aG, cG]+ bG, cG .

Геометрические свойства векторного произведения векторов:

ТМодуль вектора aG, bG равен площади Sпар параллелограмма, построен-

ного на векторах G и bG.a

Площадь параллелограмма, построенного на векторах a и bG, равна

	JJJG JJJG	G	G	G	G G
Sпар =| AD | | BE		|=| b | h =| b || a			| sin(a , b) .

50 Лекция 4

Т

Необходимым и достаточным условием коллинеарности двух векторов

является равенство нулю их векторного произведения.

Доказательство:

Необходимость. Пусть aG и b коллинеарны.

G G

G

G

G

G

G G

G

Тогда

[a , b]

=| a |

n

[a , b] = 0 .

| b | sin (a , b )= 0

Достаточность.

G G

G

G G

G

G

G G

Пусть [a,b] = 0

[a , b]

= 0

n

| a | | b | sin (a , b )= 0 .

G G

n

Тогда существуют три возможности: 1) либо sin (a , b )= 0 ,

2) либо aG = 0 ,

G G

G

G

3) либо b = 0 .

G

n

n

a коллинеарен b ; 2) и 3) a коллинеарен b

1) sin (a , b )= 0

(a

, b )= 0,

по определению.

ТВыражение векторного произведения через координаты сомножите-

лей. Если два вектора aG и b заданы своими декартовыми координатами

aG ={x1, y1, z1}, b ={x2 , y2 , z2},

то их векторное произведение имеет вид:

cG = aG, bG ={y1z2 − z1 y2 , z1x2 − x1z2 , x1 y2 − y1x2},

или в виде символического определителя (более удобном для запоминания):

						iG	Gj
	G	G	G					k
					=	x	y	z	.
	c	= a, b
						1	1	1
						x2	y2	z2

Доказательство:

Тройка {iG, Gj, k} - правая. Преобразуем:

cG = aG×bG = (x1iG + y1 Gj + z1kG)×(x2iG + y2 Gj + z2kG) = = x1 x2 iG × iG + x1 y2 iG × Gj + x1 z2 iG × k +

+y1x2 Gj ×iG + y1 y2 Gj × Gj + y1z2 Gj ×k +

+z1x2 kG×iG + z1 y2 kG× Gj + z1z2 kG×kG .

Векторная алгебра

51

Заметим, что

iG×iG = Gj × Gj = k ×kG =0, iG× Gj = −Gj ×iG = kG,

iG×kG = − kG×iG = −Gj, Gj ×kG = − kG× Gj = iG.

С учетом этих равенств выражение для c можно представить в виде:

aG, bG = ( y1z2 − z1 y2 ) i −( x1z2 − z1x2 ) Gj + (x1 y2 − y1x2 ) kG,

что можно выразить через определители:

G

=

y

z

G

x

z

G

+

x

aG, b

y

1

z

1

i −

1

z

1

j

1

2

2

x

2

x

2

2

Если два вектора aG = (x1,

y1,

z1 )

и b = (x2 ,

С

ординаты пропорциональны, то есть

x1

=

x

2

y		G	=		iG	Gj	kG		.
1		k			x	y	z
y2					1	1	1
					x2	y2	z2

y2 , z2 ) коллинеарны, то их ко-

y1 = z1 . y2 z2

4.8.Смешанное произведение векторов. Определение. Алгебраические и геометрические свойства. Выражение через декартовы координаты сомножителей

О

Т

Если вектор aG умножить векторно на вектор b , а результат aG, bG ска-

лярно умножить на вектор c , то полученное число называется смешан-
ным произведением векторов a , b , c : ( aG, b , cG)= aGbGcG.	G
G		по абсо-
Смешанное произведение некомпланарных векторов a , b ,	c

лютной величине равно объему параллелепипеда, построенного на этих

векторах, приведенных к одному началу. Оно положительно, если тройка

G

G

G

G

, b , c

a

, b , c правая и отрицательно, если она левая. Если же векторы

a

G G G

компланарны, то a b c равно нулю.

Доказательство:

Объем параллелепипеда равен произведе-

aG

нию площади основания на высоту.

S

bG, cG

осн.

=

; h =

a

cosθ

;

θ

G

bG, cG

aG

cosθ

=

c

V = Sосн. h =

G

0

G

G

= (aG , b , cG )=

aGb cG

.

b

52

Лекция 4

!Знак смешанного произведения зависит от знака cosθ : aGbGcG > 0 , если векторG aG направленG в ту же сторону, от плоскости, определяемой векторами b и c , что и вектор b, cG , т.е. когда тройка векторов правая; ана-

логично доказываетсяG, что aGb cG < 0 для левой тройки.G

Если же векторы a , b и c компланарны, то вектор c лежит в плоскостиG , определенной векторами a и b , следовательно, прeG c = 0 ([aG,b],cG)= 0 .

С1. ([aG,bG],cG)= ([bG,cG],aG)= ([cG,aG],bG), поскольку тройки aG bG cG и bG cG a , c a b

имеют одинаковую ориентацию (циклическая перестановка векторов в смешанном произведении не меняет его знака).

Нециклическая перестановка векторов в смешанном произведении

приводит к изменению ориентации тройки векторов и смене знака сме-

шанного

произведения:

GG

GG G

G G G

G GG

означает,

что

b a c

= a c b

= c b a = −ab c . Это

смешанное произведение можно записывать просто в виде

G G G

a b c , так как

G G

G

G

G

G

G

G

G

]) (смешанное

произведение зависит

от

([a,b

], c )= ([b

,c

], a)= (a

, [b

,c

порядка сомножителей, но не зависит от того, какие сомножители связаны первичным знаком векторного произведения).

2. Критерий компланарности трех векторов. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Доказательство:

Если aGbGcG = aG bG,cG cosθ = 0 , то должно выполняться хотя бы одно из

условий:
1)		aG		= 0 => векторы компланарны;
2)				G	G		=		G
		b			,c			0 , если b и c коллинеарны, => a , b , c - компланарны;
								, тогда aG			G
3)	cosθ = 0
										b, cG , т.е. a компланарен b и c .
								G	G G
Обратно, если a									, b , c - компланарны и не имеют место случаи 1) и 2),

то имеет место случай 3).

Векторная алгебра

53

Выражение смешанного произведения через

декартовы координаты сомножителей

Если три вектора

G

,

G

и

c

заданы своими декартовыми координатами

Т

a

b

G

G

G

+ z1kG,

G

G

G

G

G

G

a

= x1i + y1 j

Gb

= x2i

+ y2 j

+ z2k

,

c = x3i

+ y3 j + z3k ,

то смешанное

произведение a b c

равняется определителю,

строки которого соответ-

ственно равны координатам перемножаемых векторов:

G

G

G

x1

y1

z1

.

a b c =

x

y

2

z

2

2

x3

y3

z3

Доказательство:

iG

Gj

kG

G

cG =

G

y

z

G

x

z

G

x

y

,

b ,

x

y

2

z

2

= i

2

2

− j

2

2

+ k

2

2

2

y3

z3

x3

z3

x3

y3

x3

y3

z3

G

G

x1

y1

z1

G

y2

z2

x2

z2

x2

y2

(a, b ,

c )= x1

y

z

− y1

x

z

+ z1

x

y

=

x2

y2

z2

.

3

3

3

3

3

3

x3

y3

z3

СНеобходимым и достаточным условием компланарности трех векторов, заданных в декартовом базисе, является равенство нулю определителя третьего порядка, в первой строке которого записаны координаты первого вектора, во второй - второго, в третьей - третьего.

В результате изучения материала, изложенного в этой лекции, студент должен знать:

различия между скалярными и векторными величинами;

определения и свойства линейных операций над векторами (сложение и умножение на число);

понятие базиса и координат вектора в данном базисе;

определения скалярного, векторного и смешанного произведений;

алгебраические и геометрические свойства произведений векторов;

выражение произведений векторов через координаты сомножителей;

что вычисляется с помощью произведений векторов: скалярного (число) – длины векторов, углы, проекции,

векторного (вектор) – площади треугольников и параллелограммов, смешанного (число) – объемы.

Лекция 5 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.

ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

Предметом изучения аналитической геометрии является описание геометрических объектов на плоскости и в пространстве с помощью уравнений. Методы аналитической геометрии широко используются в современном естествознании и прикладных технических дисциплинах при построении математических моделей объектов и процессов. В лекции 5 рассматриваются наиболее простые объекты, описываемые уравнениями первой степени – плоскости и прямые. Приводятся различные виды уравнений плоскостей и прямых в пространстве, показывается, для какого типа задач тот или иной тип более уместен. Примеры иллюстрируют методы решения типичных задач.

5.1.Основы аналитической геометрии

5.1.1.Уравнение поверхности

5.1.2.Уравнения линии

5.2.Плоскость в пространстве

5.2.1.Плоскость как поверхность первого порядка. Общее уравнение плоскости.

5.2.2.Неполные уравнения плоскостей

5.2.3.Уравнения плоскости «в отрезках»

5.2.4.Нормальное уравнение плоскости

5.2.5.Расстояние от точки до плоскости

5.2.6.Уравнение плоскости, проходящей через три данные точки

5.2.7.Угол между двумя плоскостями

5.2.8.Условие параллельности и перпендикулярности плоскостей

5.3.Прямая линия в пространстве

5.3.1.Векторное уравнение прямой

5.3.2.Параметрические уравнения прямой

5.3.3.Канонические уравнения прямой

5.3.4.Уравнения прямой, проходящей через две данные точки

5.3.5.Общие уравнения прямой

5.3.6.Уравнение пучка плоскостей, проходящих через прямую

5.3.7.Угол между двумя прямыми. Условия параллельности

иперпендикулярности двух прямых

5.4.Прямая и плоскость

5.4.1.Точка пересечения прямой и плоскости

5.4.2.Угол между прямой и плоскостью. Условия параллельности

иперпендикулярности прямой и плоскости