биофизика

ГЛАВА 7. ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТИ.

Наблюдаемые нами события можно разделить на следующие три вида: достоверные, невозможные и случайные. Достоверным называют событие, которое обязательно произойдет, если будет выполнена определенная совокупность условий М.

Пример 1. Рассмотрим воду при нормальном атмосферном давлении и температуре 200С. Событие "вода находится в жидком состоянии" – есть достоверное.

Невозможным называют событие, которое заведомо не произойдет, если будет выполнена совокупность условий М.

Пример 2. Событие "вода находится в твердом состоянии" заведомо не произойдет при условии предыдущего примера.

Случайным называют событие, которое при выполнении условий М может либо произойти, либо не произойти.

Пример 3. Подбрасывается монета. Она может упасть гербом или надписью. Событие "при бросании монеты выпал герб" – случайное.

Теория вероятностей не ставит перед собой задачу предсказать, произойдет конкретное событие или нет. Другое дело, если рассматриваются случайные события, которые могут многократно наблюдаться при выполнении одних и тех же условиях М, т.е. если речь идет о массовых однородных случайных событиях. Оказывается, что они подчиняются определенным закономерностям, которыми и занимается теория вероятностей.

7.1. СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ ВЕРОЯТНОСТИ.

7.1.1. Основные понятия теории вероятностей.

Мы уже говорили, что событие называется случайным, если оно может произойти, либо не произойти при определенных условиях М. В дальнейшем вместо слов "совокупность условий М осуществлена" будем говорить: "произведено испытание". Т.е. событие будет рассматриваться как результат испытания – рис.7.1.

Ω Здесь Ω - множество всех элементарных событий. Любое подмножество А множества Ω

Аназывается событием.

Рис. 7.1. Геометрическая иллюстрация события

232

Пример 4. В ящике лежат цветные шары. Из него наудачу берут один шар. Извлечение шара из ящика – есть испытание. Название шара определенного цвета – событие. Установим некоторые соотношения между событиями, с которыми приходится иметь дело в теории вероятностей. Будем обозначать случайные события большими латинскими буквами А,В,С,... Достоверное событие будем обозначать U, а невозможное V.

Определение 1. События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании – рис. 7.2.

Ω

В

А

Рис. 7.2. Иллюстрация несовместных событий

Пример 5. Брошена монета. Появление герба исключает появление надписи. События "появился герб" и "появилась надпись"

– несовместные.

Определение 2. Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них – рис. 7.3.

Рис. 7.3. Полная группа событий

Пример 6. Бросается игральная кость (кубик с цифрами от 1 до 6). Обязательно произойдет одно из следующих событий – выпадение 1,2,...6. Эти несовместные события образуют полную группу.

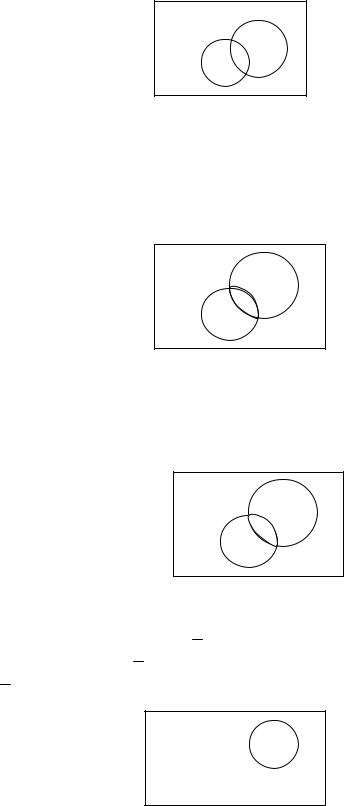
Определение 3. Суммой А В (А+В; А или В) называют событие, заключающееся в появлении события А или В, или обоих событий А и В вместе. – рис.7.4.

233

Ω

В

А

Рис. 7.4. Сумма событий

Определение 4. Произведением или совмещением событий А и В называют событие С, равносильное совместному наступлению обоих событий С=А ∩ В(С=А В; С=А и В) – рис. 7.5.

Если А В= , то события несовместные (нет области совмещения).

Ω

В

А

Рис. 7.5. Произведение событий

Определение 5. Разностью событий А и В называется событие, состоящее из тех элементарных событий, которые входят в А и не входят в В. – рис. 7.6.

Ω

В

А

Рис. 7.6. Разность событий

Определение 6. Событие A (не А) называется противоположным событию А, если A A = и

A + A = Ω . – рис. 7.7.

ΩА

А

Рис. 7.7. Противоположные события

234

7.1.2. Классическое определение вероятности.

Вероятность события характеризует степень объективной возможности этого события. пусть в данном испытании мы различаем полную группу, состоящую из n попарно несовместных и равновозможных событий А1, А2, ... Аn , которые будем называть элементарными исходами данного испытания, или элементарными событиями.

Определение. Если множество Ω состоит из n равновозможных элементарных событий, то вероятность Р(А) события А равна числу m элементарных событий. входящих в А, деленному на число всех элементарных событий, т.е.

Случай равновозможных событий называется "классическим", поэтому вероятность (7.1) часто называют "классической". Элементарные события, входящие в А (исходы опыта) называются "благоприятствующими". Таким образом, можно дать более короткое определение:

Определение. Вероятность случайного события А равна отношению благоприятствующих событию А исходов к общему числу элементарных исходов.

Пример 1. В клетке имеется 10 мышей: 3 белых и 7 серых. Наугад вытаскивается одна мышь. Какова вероятность того, что:

а) мышь белая, б) мышь серая.

Решение:

В соответствии с формулой (7.1) имеем:

а) n=10, m=3. Вероятность вытащить белую мышь равна P1 = 103 .

б) n=10, m=7. Вероятность вытащить серую мышь равна P2 = 107 .

Замечание. Слово "наугад" в задачах следует понимать как равновозможность элементарных исходов.

Свойства вероятности.

Из определения вероятности вытекают следующие ее основные свойства.

Свойство 1. Вероятность достоверного события равна единице. Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. в этом

случае m = n , следовательно

235

Свойство 2. Вероятность невозможного события равна нулю. Действительно, если событие невозможно, то ни один из

элементарных исходов не благоприятствует событию. В этом случае m = 0 , следовательно

положительное число, заключенное между 0 и 1.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом

Комбинаторика.

В большинстве задач на классическую вероятность величины m и n не являются столь очевидными, как в примере 1. В этих случаях для вычисления m и n используются законы комбинирования вариантов, основные из которых рассмотрены ниже.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

Пример 2. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа один раз.

Решение:

Сначала перепишем все возможные комбинации:

123, 132, 213, 231, 312, 321, т.е. всего 6. П формуле (7.5) имеем:

P3 = 3!=1 2 3 = 6

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число размещений

Пример 3. Сколько можно составить сигналов из шести флажков различного цвета, взятых по два.

Решение:

Взяв в качестве цвета флажков первые буквы Б, К, С, З, Ж, Г, выпишем возможные комбинации пар:

236

A62 = 6 5 = 30

Сочетаниями называют комбинации. составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом.

Число сочетаний:

Перестановки, размещения и сочетания связаны равенством

По этой формуле сочетания вычисляются быстрее, чем по (7.7) Пример 4. Сколькими способами можно выбрать 2 ампулы из

упаковки, содержащей 10 ампул.

Решение:

Из формулы (7.8.) имеем:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Правило произведения. Если некоторый объект А можно выбрать из совокупности объектов m способами, а объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m n способами.

Пример 5. У 6 мальчиков и 11 девочек имеются признаки инфекционного заболевания. Чтобы проверить наличие заболевания, требуется взять выборочный анализ крови у 2 мальчиков и 2 девочек. Сколькими способами можно это сделать?

Решение:

Количество способов выбора двух мальчиков:

n1 = C62 = 26!9!! =15 способов.

Количество способов выбора двух девочек:

n2 = C42 = 211!9!! = 55 способов.

Т.к. каждая пара мальчиков может быть взята с каждой парой девочек, то по правилу произведения имеем:

237

N = n1 n2 =15 55 = 825 способов.

Примеры.

6. Технический контроль из партии в 10 изделий проверяет взятые наудачу 3 изделия. Партия не принимается, если среди трех проверяемых изделий окажется хотя бы одно бракованное. Определить вероятность приемки партии, если в ней окажется 5 бракованных изделий.

Решение:

Обозначим через А событие, состоящее в том, что партия изделий будет принята. Общее число элементарных исходов, состоящее в проверке трех наудачу взятых изделий из 10, равно n = C103 , т.е. число сочетаний из 10 по 3.

7. При наборе телефонного номера абонент забыл две последние цифры и наудачу набрал их, помня только, что эти цифры нечетные

иразличные. Найти вероятность того. что номер набран правильно.

Решение:

Вэтой задаче порядок набора цифр важен. поэтому для определения числа всех возможных исходов следует использовать размещения. Число благоприятных исходов m равно 1, т.к. правильным является только один номер. Следовательно, искомая вероятность равна:

8. Пусть в группе из 10 человек - четверо мужчин. Если случайным образом выбирают двух человек, то какова вероятность, что это:

а) оба мужчины, б) обе женщины,

в) один мужчина и одна женщина.

Решение:

Обозначим события:

А – выбирают двух мужчин, В – выбирают двух женщин,

С – выбирают одного мужчину и одну женщину. Число всех исходов:

238

n = C102 = 102!8!! = 45

Число выбора двух мужчин из четырех:

m1 = C42 = 6

Число способов выбора двух женщин из шести:

m2 = C62 =15

По формуле (7.1) имеем:

Наконец, существует 4 способа выбора одного мужчины и 6 способов выбора одной женщины. По правилу произведения число способов выбора двух человек обоего пола равно:

m3 = 6 4 = 24 и P(C) = 2445 = 158 .

9. Из 20 человек одновременно заболевших гриппом, 15 выздоровели полностью за 3 дня. Предположим, что из этих 20 человек случайным образом выбирают 5. Какова вероятность того, что за 3 дня из этих человек выздоравливают:

а) 5 человек, б) 4 человека,

в) никто не выздоравливает.

Решение:

Обозначим события:

А – за 3 дня выздоравливают 5 человек. В – за 3 дня выздоравливают 4 человека. С – за 3 дня не выздоравливают никто.

Число всех исходов равно

Число способов выбора из 15 выздоровевших пяти человек –

m1 = C155 = 3003 .

Таким образом P(A) = 155043003 = 0,194 . Число способов выбора из 15

выздоровевшего из пяти - C51 = 5

По правилу произведения, число способов выбора 5 человек, из которых выздоравливают за 3 дня только четверо, равно

m2 = C154 C51 =1365 5 = 6825 . Следовательно P(B) = 155046825 = 0,440 .

239

Число способов выбора пяти не выздоровевших за три дня из пяти

равно 1 иP(C) = 155041 = 0,00006 .

10. На полке 6 книг по математике и 4 по физике. Найти вероятность того, что среди выбранных наудачу пяти книг будут три по математике и две по физике.

Решение:

Найдем число способов выбора: 3 книги по математике m1 = C63 = 20 2 книги по физике m2 = C42 = 6 .

Пять книг, среди которых три по математике и две по физике. по правилу произведения – m = m1 m2 = 20 6 =120 .

Число всех исходов равно n = C105 = 252 . Искомая вероятность по

формуле (7.1) равна:

P = 120252 = 3063 .

11. В клетке 6 белых и 4 серых мыши. Случайным образом извлекают 3 мыши. Вычислить вероятность для 4 возможных комбинаций цвета мыши.

Решение:

Обозначим:

б – белая мышь с – серая мышь

A1, А2, А3, А4 – события, состоящие в появлении одной из возможных комбинаций цвета мышей: ббб, ссс, бсс, ббс.

Число всех исходов равно

n = C103 = 101 29 38 =120 ,

(всего мышей 10, выбираем 3).

Число способов выбора из 6 белых мышей трех равно

m1 = C63 = 61 25 34 = 20 и P(A2 ) = 12020 = 16 .

Число способов выбора из 4 серых мышей трех равно

m2 = C43 = 14 23 32 = 4 и P(A2 ) = 1204 = 301 .

Событие A3 состоит в том, что из 6 белых мышей нужно выбрать одну – это C61 = 6 способов , и из четырех серых мышей выбрать две

– это C42 = 6 способов. Общее количество вариантов будет равно

m3 = C61 C42 = 36 , а P(A3 ) = 12036 = 103 .

Рассуждая аналогично, найдем общее число способов выбора двух белых и одной серой мыши – событие A4 .

240

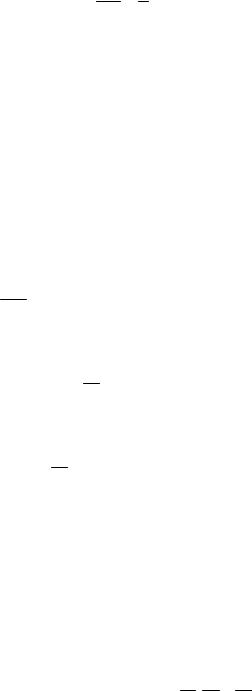
m4 = C62 C41 =15 4 = 60 , а P(A4 ) = 12060 = 12 .

12. В коробке 5 одинаковых изделий, причем 3 из них окрашены. наугад извлечены 2 изделия. Найти вероятность того, что среди отобранных:

а) одно окрашено, б) два окрашены,

в) хотя бы одно окрашено.

Решение:

Обозначим события:

А– окрашено одно изделие из двух извлеченных,

В– окрашены два,

С – хотя бы одно окрашено.

Число всех исходов определяется как

n = C52 = 15 24 =10 .

а) Так как окрашено одно изделие, то второе не окрашено и, следовательно,

m1 = C31 C21 = 3 2 = 6 , а P(A) = 106 = 0,6 .

б) поскольку из двух извлеченных изделий окрашены два, то неокрашенных нет вовсе и

m2 = C32 = 3, и P(B) = 103 = 0,3 .

в) Когда мы говорим "хотя бы одно окрашено", то имеем ввиду, что окрашенных изделий может быть одно или два. Тогда искомая вероятность находится как сумма вероятностей.

P(C) = P(A) + P(B) = 0,6 + 0,3 = 0,9 .

Замечание. Если, в задаче требуется найти вероятность появления "хотя бы одного" события из нескольких А1, А2, ... Аn, то в этом случае удобно пользоваться формулой:

где q1, q2 ,...qn - вероятности противоположных событий A1, A2 ,...An .

В нашем примере противоположным событием будет – "ни одно изделие не окрашено". Следовательно,

Оба результата совпали.

13. Из полного набора костей домино наугад берутся пять костей. Найти вероятность того, что среди них будет хотя бы один с шестеркой.

241