Ан. геометрия

1.Вектором (геометрическим вектором) 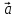называется множество всех направленных отрезков, которые имеют одинаковую длину и направление. О всяком отрезке из этого множества говорят, что он представляет вектор 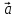. Алгебраические операции над векторами: сложение, вычитание, умножение вектора на число.

2.

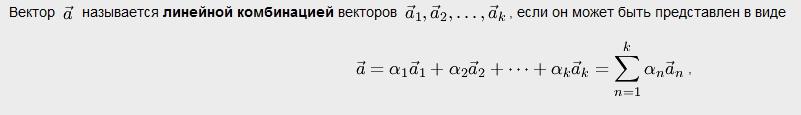
3.

Вектора называются компланарными, если они лежат в одной плоскости. Аналогично, в пространстве любой вектор можно разложить в базисе троих некомпланарных векторов.

4.

5.Скалярным произведением двух векторов называется величина, которая равна произведению длин этих векторов на косинус угла между ними.

Проекция одного вектора на другой и угол между ними определяются по формулам:

Работа силы потраченая на перемещение определяется по формуле:

6.Скалярное произведение векторов в координатах определяется по формуле:

Свойства:

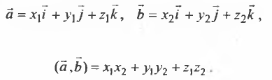
7.Векторным произведением двух векторов называется третий вектор, который удоблетворяет следующие условия:

Свойства:

8.Векторное произведение в координатах можно получить с помощью определителя:

Площадь паралелограмма S₁ и площадь S₂ треугольника определяются по формулам:

Момент силы приложеной к точке относительно оси определяется по формуле:

9.Смешаным произведением тройки векторов называется скалярное произведение вектора

. Т.е.

Свойства:

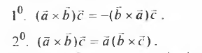
10.Смешаное произведение в координатах равно:

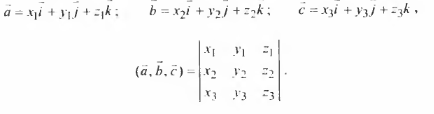
Объем паралилепипеда V₁ и объем пирамиды V₂ определяется по формулам:

11.

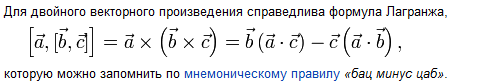
12.Векторное уравнение прямой:

Параметрическое уравнение:

Каноническое уравнение:

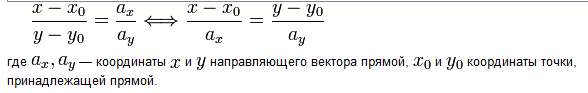
Уравнение прямой проходящей через две точки:

, точки M₁(x₁;y₁) и M₂(x₂;y₂).

13.Общее уравнение прямой на плоскости:

Уравнение с угловым коефициентом:

Уравнение в отрезках:

14.Нормальное уравнение прямой:

Если задано общее уравнение прямой и точка, то расстояние от этой точки до прямой разсчитывается по формуле:

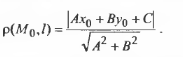
15.Прямые на плоскости могут пересекаться (частный случай быть перепендикулярными), быть паралельными (частный случай совпадать).

16. Определение. Пучком прямых на плоскости называется множество всех прямых данной плоскости, имеющих одну общую точку, которая называется центром пучка.

17. Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;

Векторное уравнение:

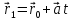
Общее уравнение:

18.Уравнение плоскости в отрезках:

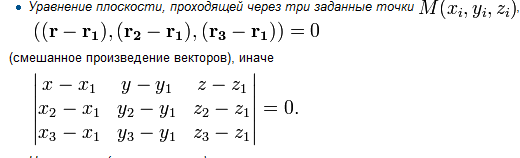
Плоскости могут пересекаться (частный случай быть перпендикулярными) и быть параллельными (частный случай совпадать).

19.Нормальное уравнение плоскости:

Расстояние 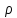от точки до плоскости:

20.Уравнение связки плоскостей:

Уравнение пучка плоскостей:

21.Общее уравнение прямой в пространстве:

Параметрическое уравнение прямой:

,t – параметр.

Векторное уравнение:

Каноническое уравнение:

22.Прямая и плоскость могут пересекаться (частный случай быть перпендикулярными) и быть паралельными (частный случай прямая принадлежит плоскости).

23. Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F1 и F2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

| F1M | + | F2M | = 2a, причем | F1F2 | < 2a.

24. Эксцентриситет — числовая характеристика конического сечения, показывающая степень его отклонения от окружности. Обычно обозначается “e” или “ε”.

Директриса — прямая, лежащая в плоскости конического сечения (эллипса, гиперболы или параболы) и обладающая тем свойством, что отношение расстояния от любой точки кривой до фокуса кривой к расстоянию от той же точки до этой прямой есть величина постоянная, равная эксцентриситету.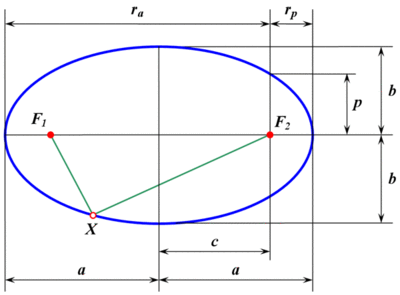

Оптические свойства эллипса

• Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.

• Свет от источника, находящегося вне любого фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.

25.

26.

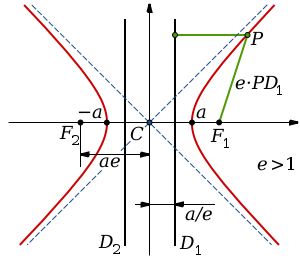
27.Определение кривой второго порядка через директрису и эксцентриситет:

29.Общее уравнение кривой второго порядка:

Уравнение вида Ax²+Cy²+2Dx+2Ey+F=0 всегда определяет либо

окружность (при А=С), либо эллипс (при А*С>0), либо гиперболу (при

А*С<0), либо параболу (при А*С=0), при этом возможны случаи вырождения: для

эллипса (окружности) – в точку или мнимый эллипс (окружность), для гиперболы –

в пару пересекающихся прямых, для параболы – в пару параллельных прямых.

Общее уравнение второй степени с двумя неизвестными: Ax²+2Bxy+Cy²+2Dx+2Ey+F=0

Коэффициент В с произведением координат преобразовывает уравнение путем

поворота координатных осей.

30. Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты, которых удовлетворяют уравнению вида:

a₁₁x² + a₂₂y² + a₃₃z² + 2a₁₂xy + 2a₂₃yz + 2a₁₃xz + 2a₁₄x + 2a₂₄y + 2a₃₄z + a₄₄ = 0

в котором, по крайней мере, один из коэффициентов a₁₁, a₂₂, a₃₃, a₁₂, a₂₃, a₁₃ отличен от нуля.

Эллипсоид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:

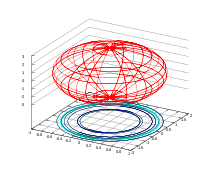
Величины a, b, c называют полуосями эллипсоида. Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка.

Гиперболоид (от др.-греч. ὑπερβολή — гипербола, и εἶδος — вид, внешность). В математике гиперболоид — это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением

  (однополостный гиперболоид),

где a и b — действительные полуоси, а c — мнимая полуось;

или

  (двуполостный гиперболоид),

где a и b — мнимые полуоси, а c — действительная полуось.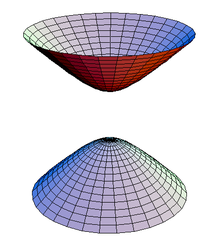

Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси, двухполостный — вокруг действительной. Двухполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: | AP − BP | = const. В этом случае A и B называются фокусами гиперболоида.

Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.

31. Коническая поверхность — поверхность, с вершиной O и направляющей G, содержащая все точки всех прямых, проходящих через точку O и пересекающихся с кривой G.

Каноническое уравнение круговой конической поверхности в декартовых координатах .

Эллипти́ческий параболо́ид — поверхность, описываемая функцией вида

,

где a и b одного знака. Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.

Если a = b то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину данной параболы.

Гиперболи́ческий параболо́ид (называемый в строительстве «гипар») — седлообразная поверхность, описываемая в прямоугольной системе координат уравнением вида

 .

Из второго представления видно, что гиперболический параболоид является линейчатой поверхностью.

Поверхность может быть образована движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается со второй своей вершиной.

32.Цилиндры:

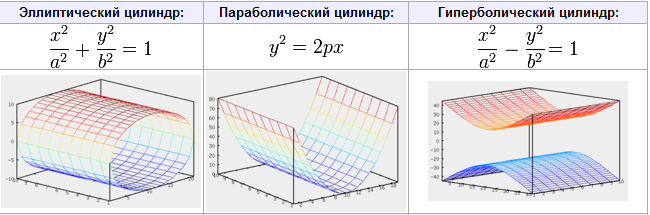
Вырожденные поверхности второго порядка – это конусы и цилиндры.