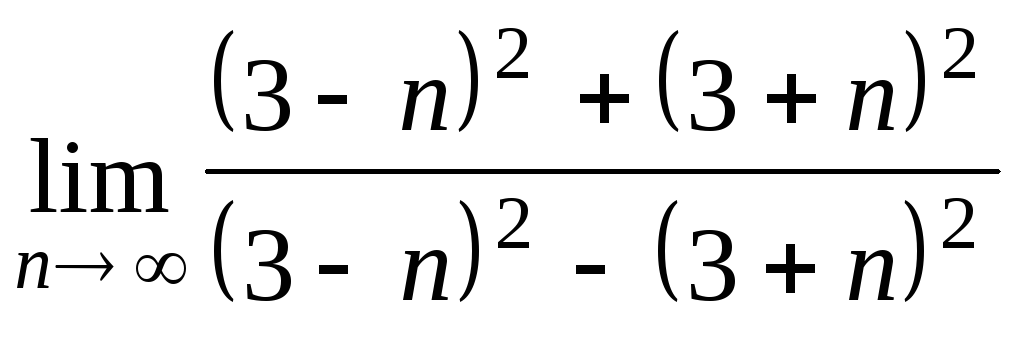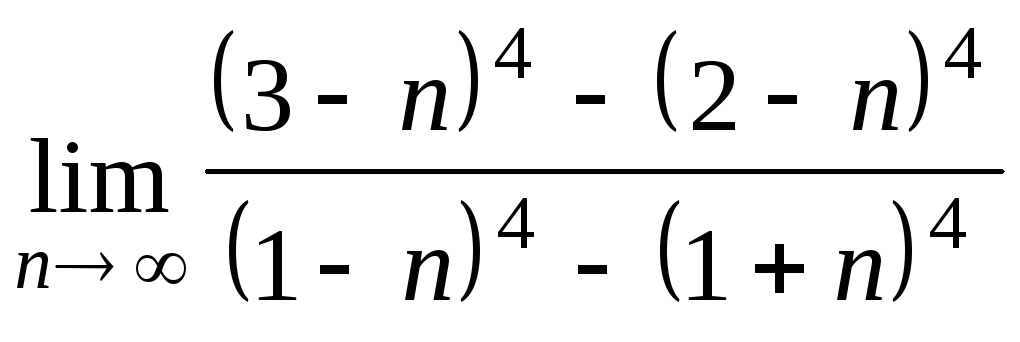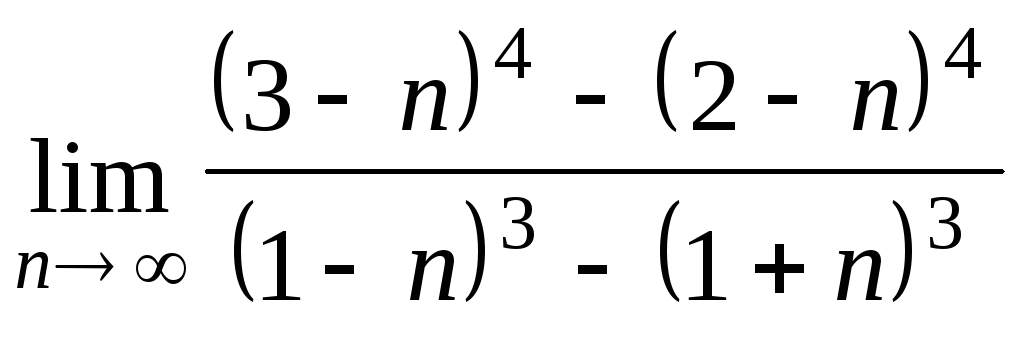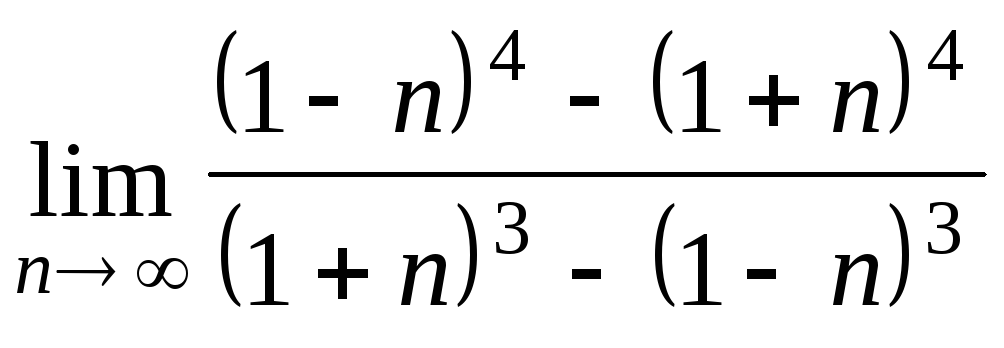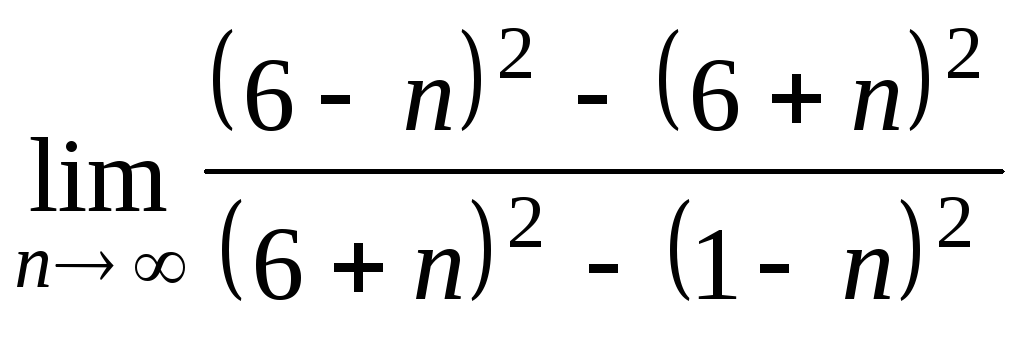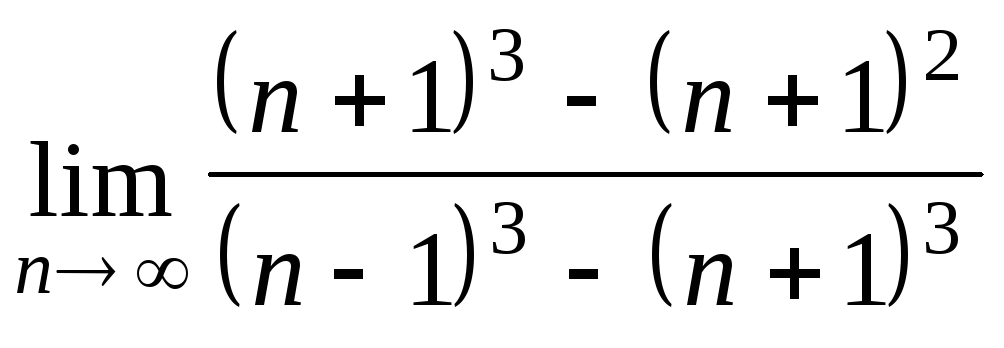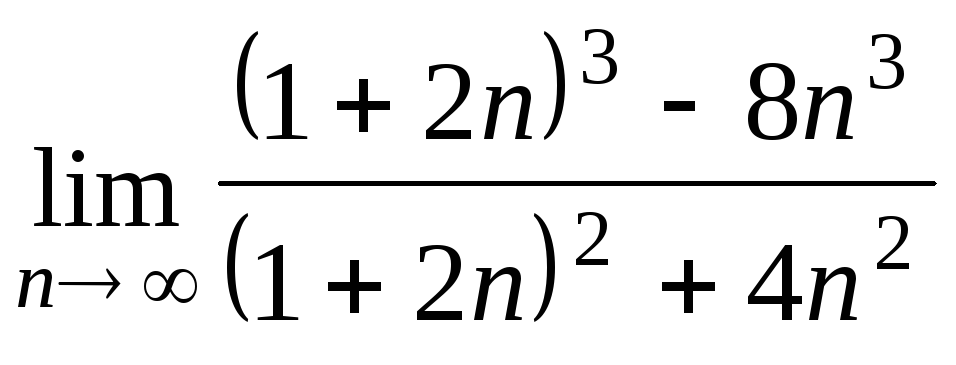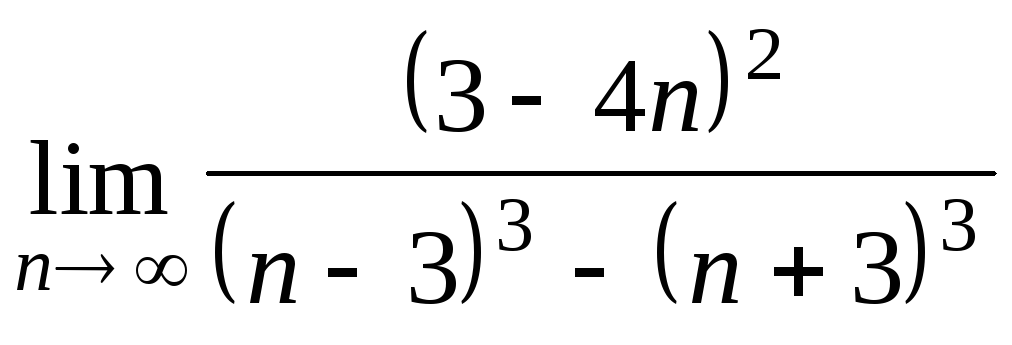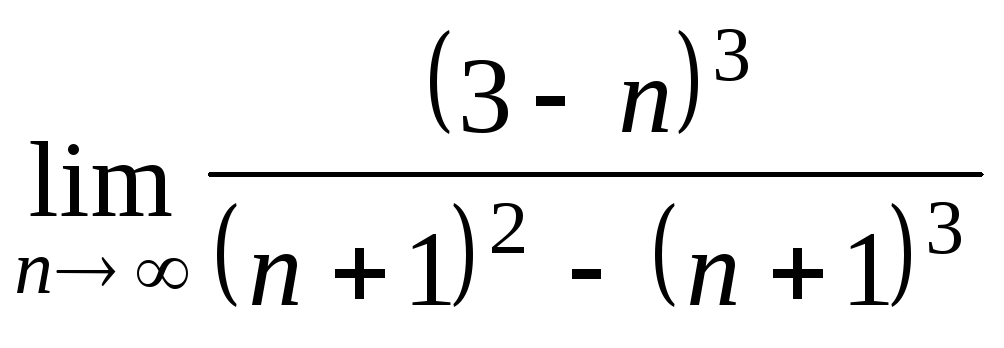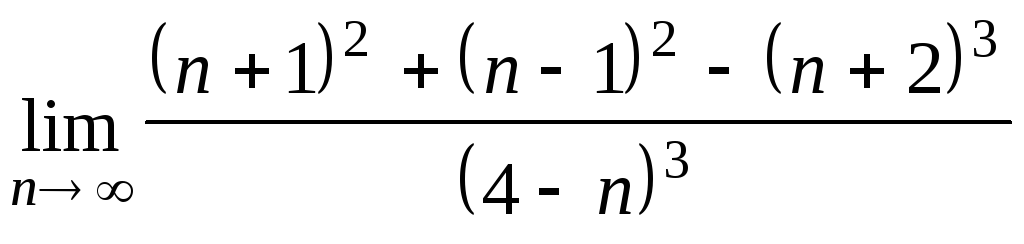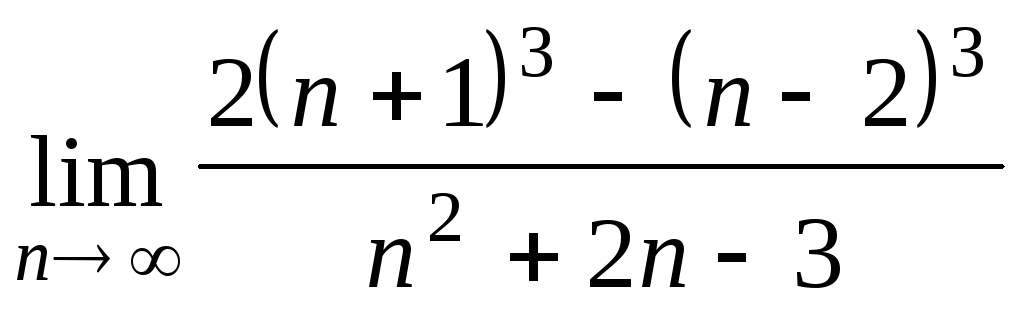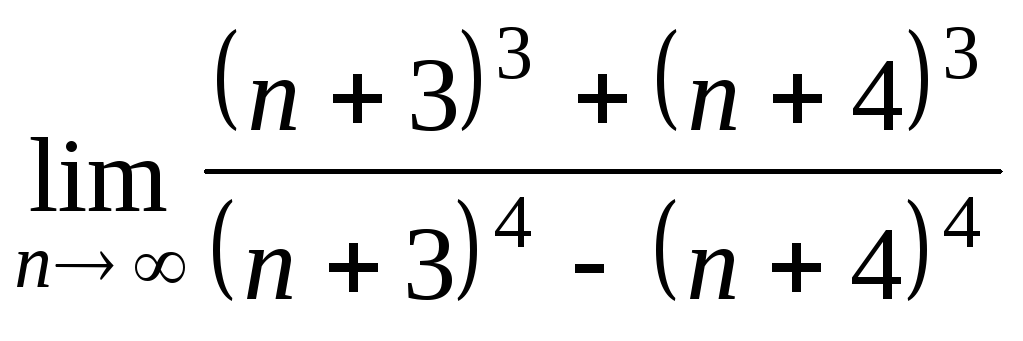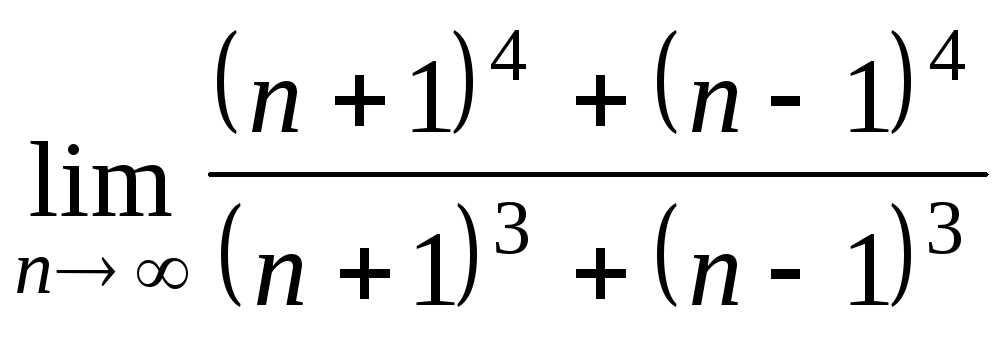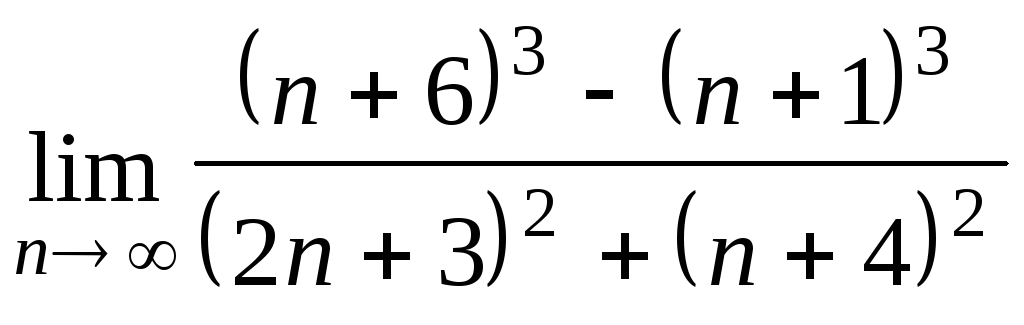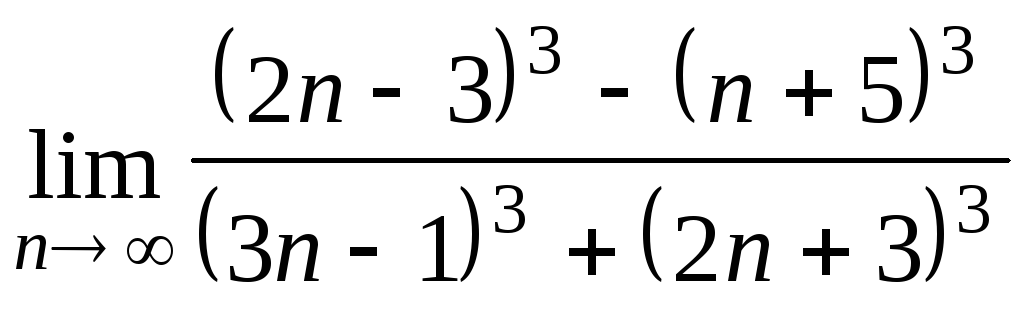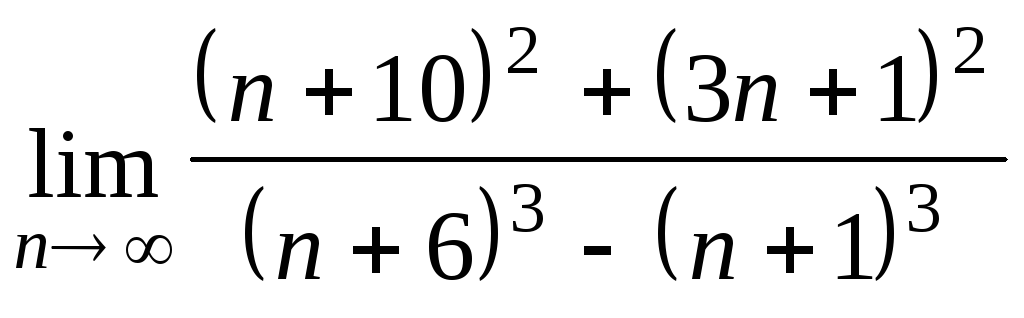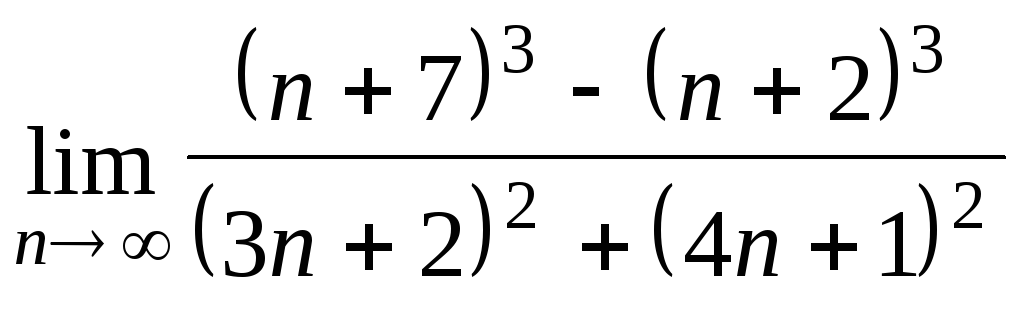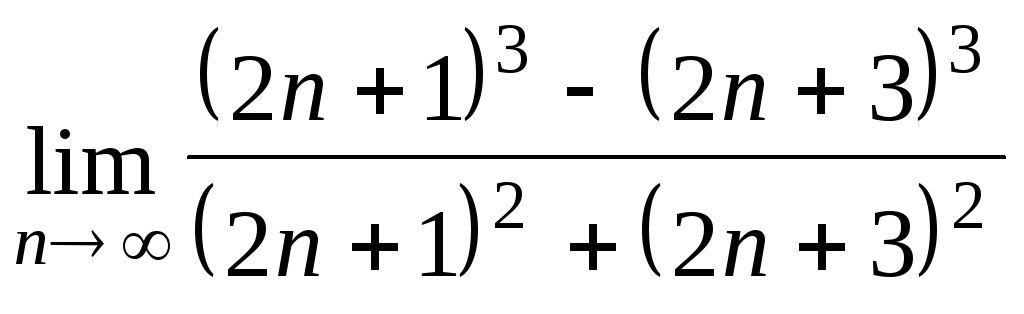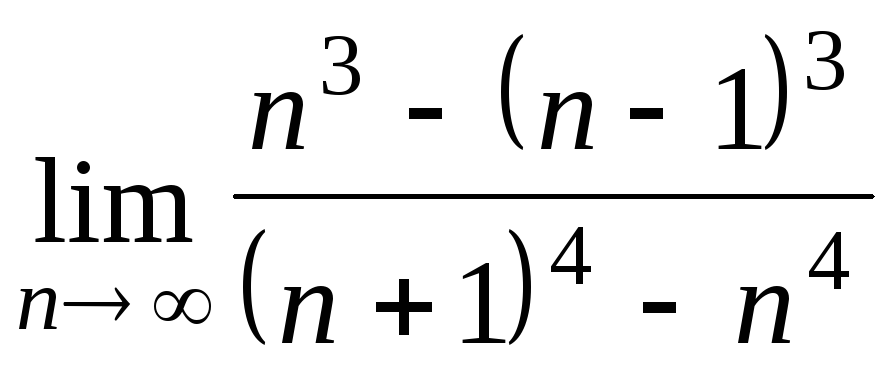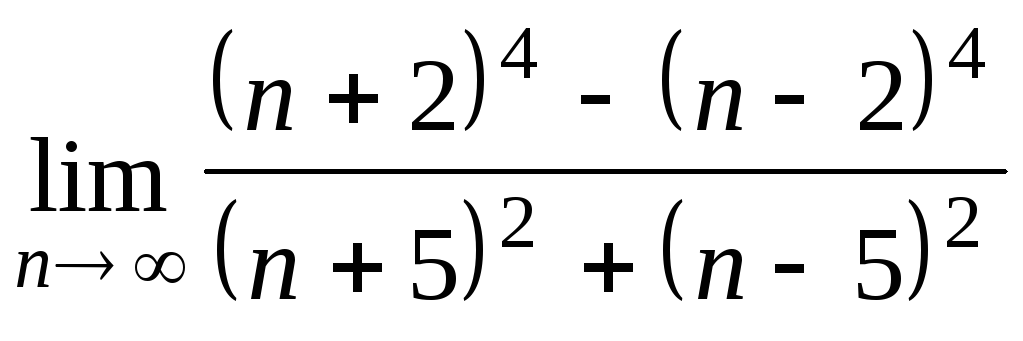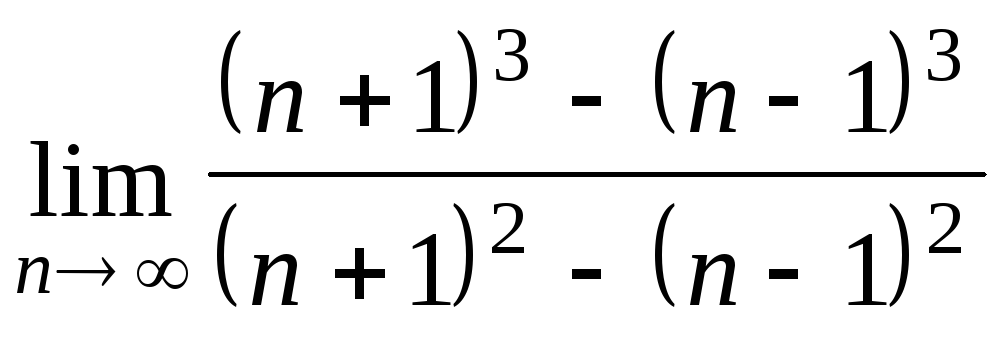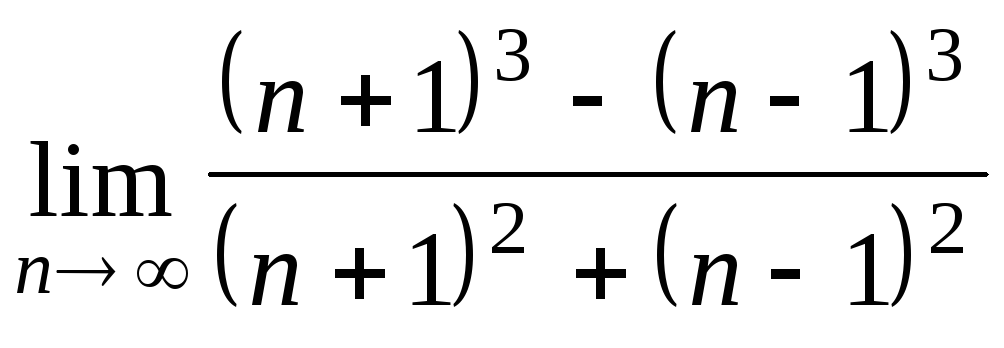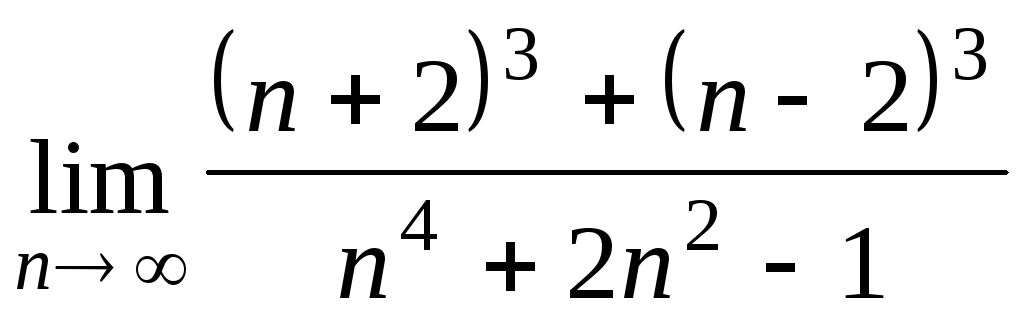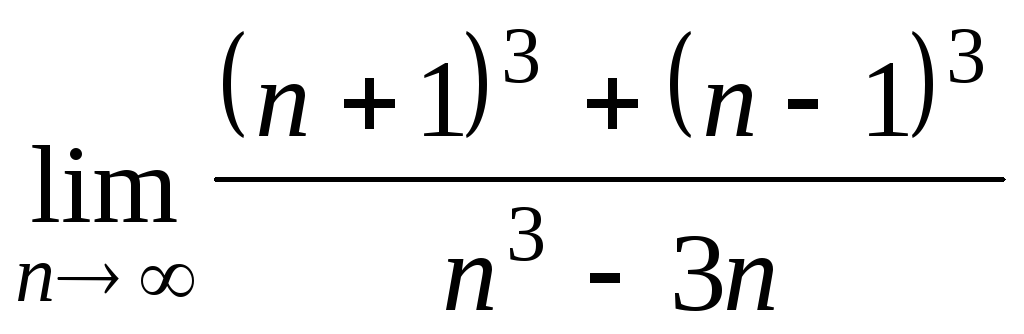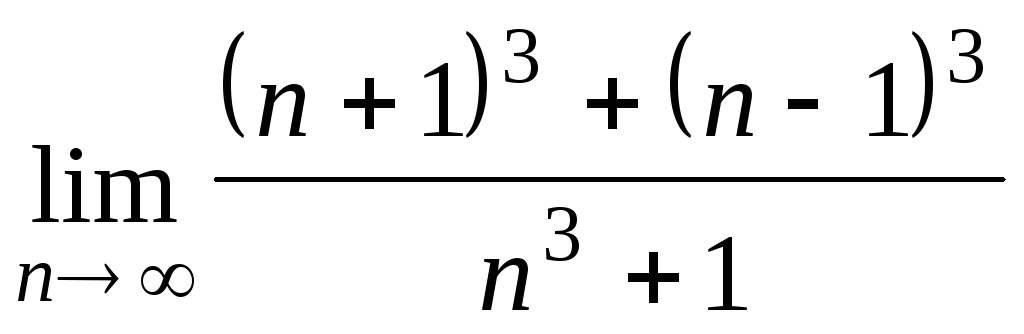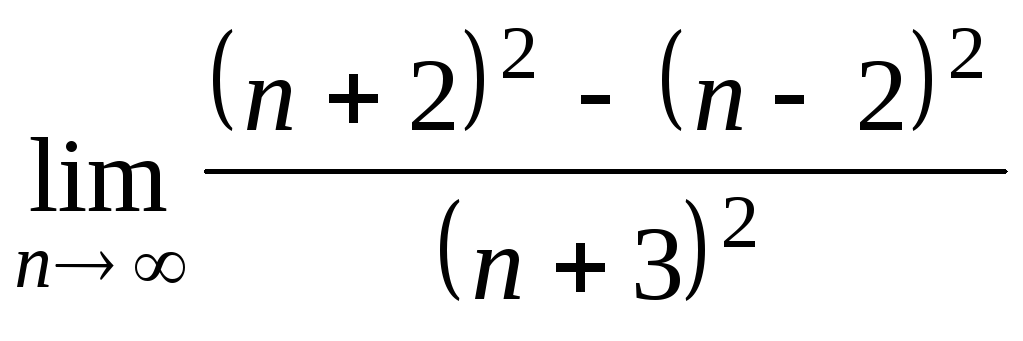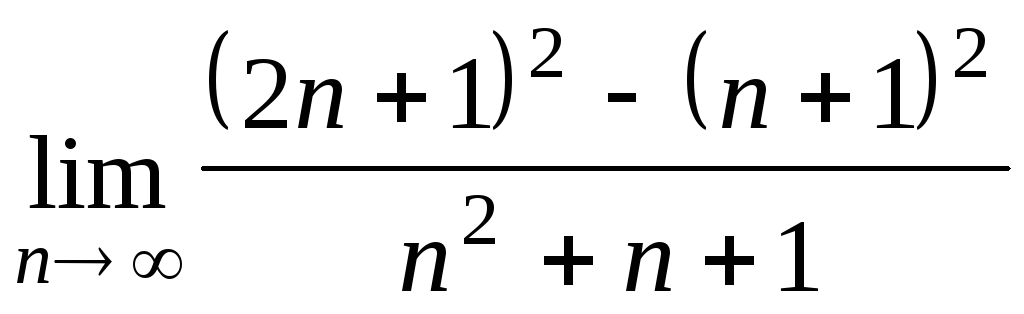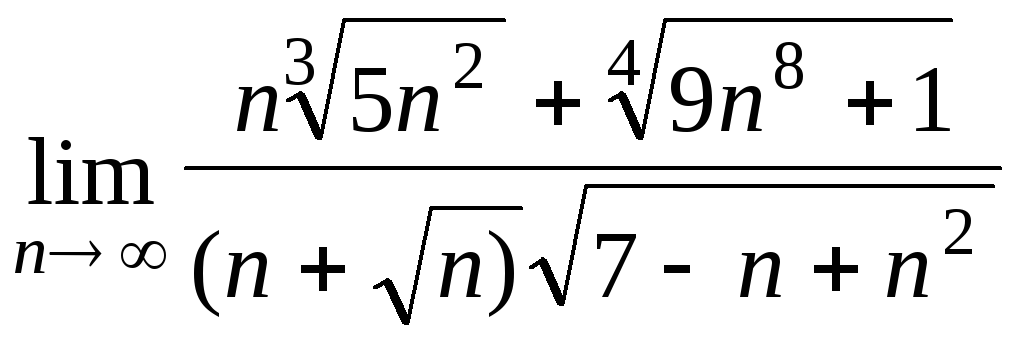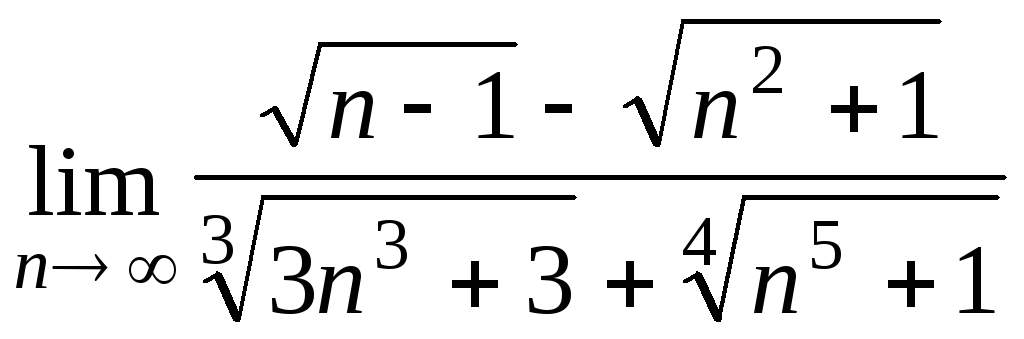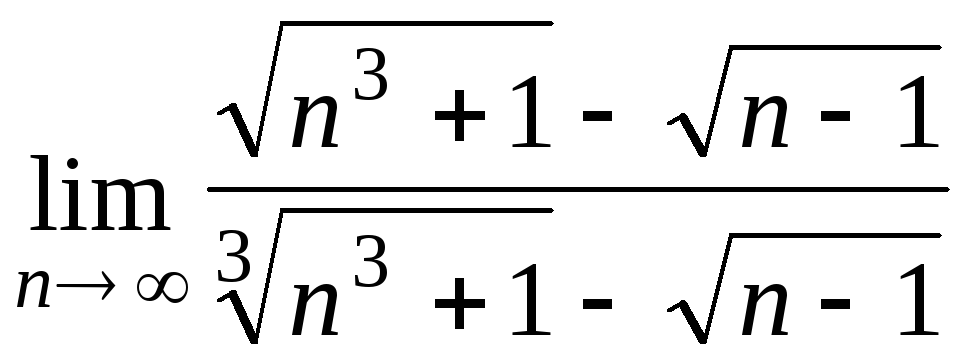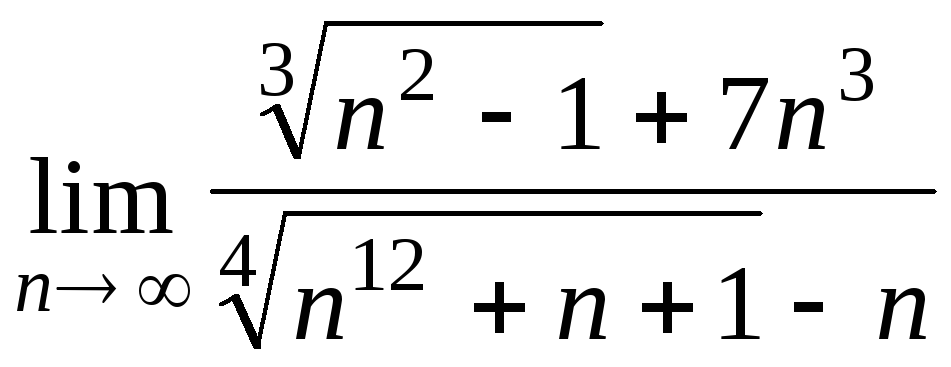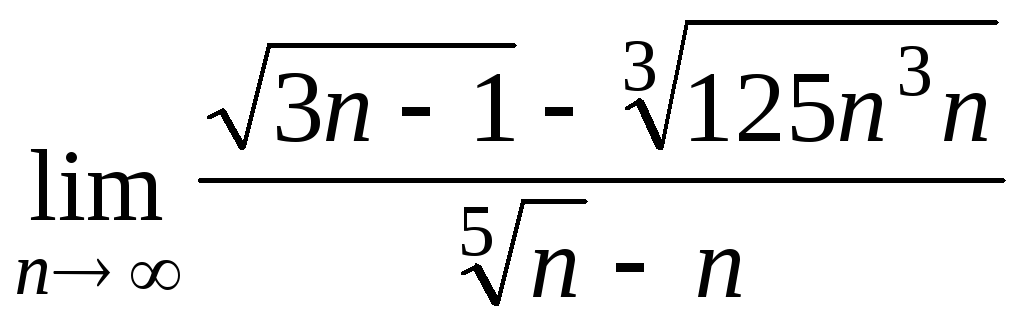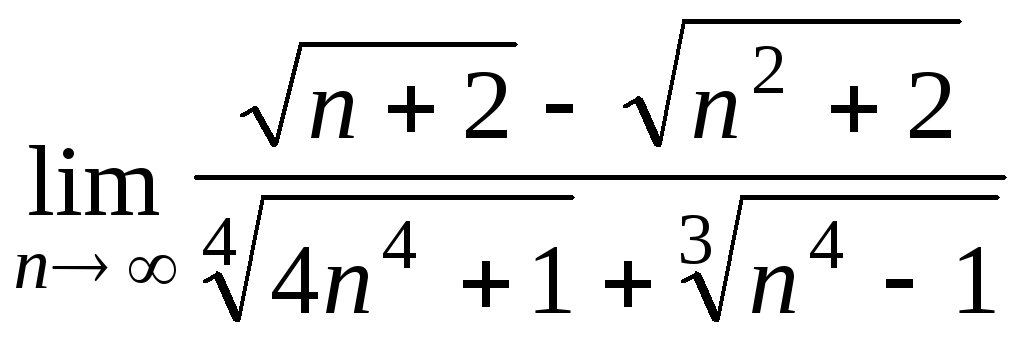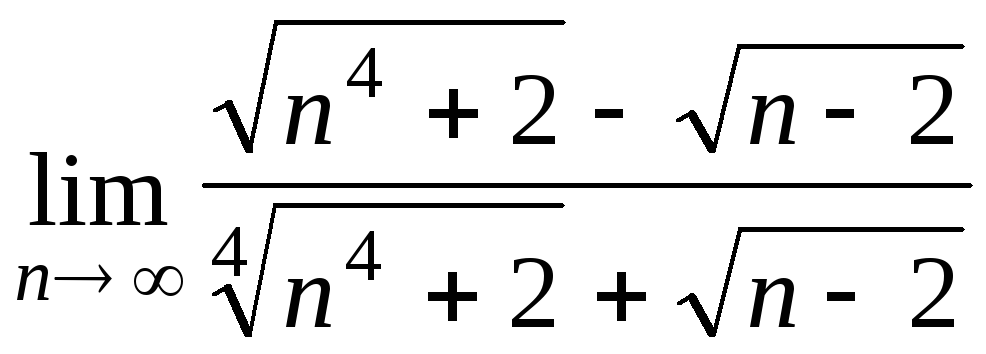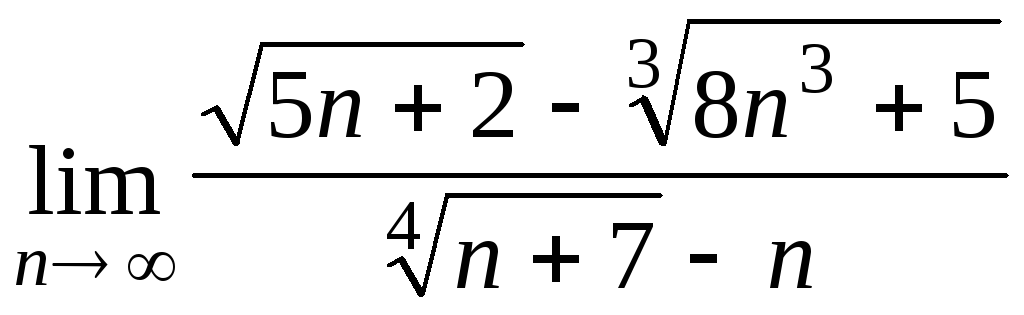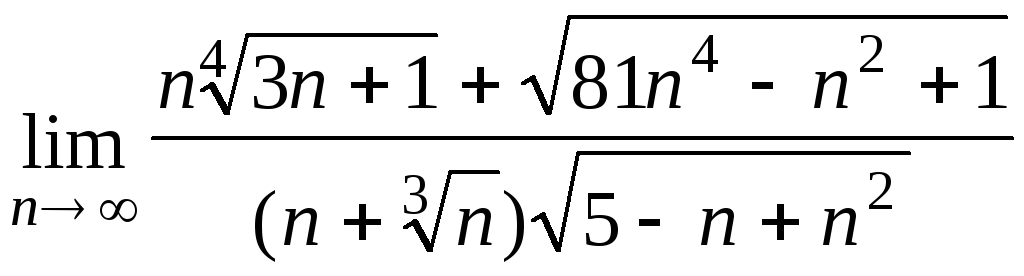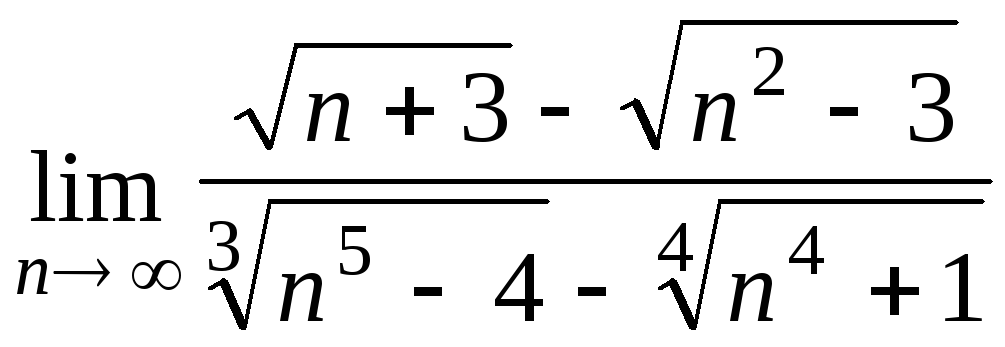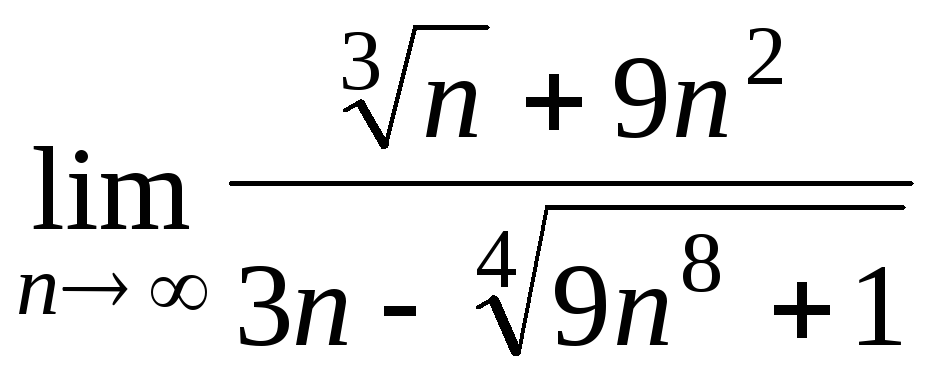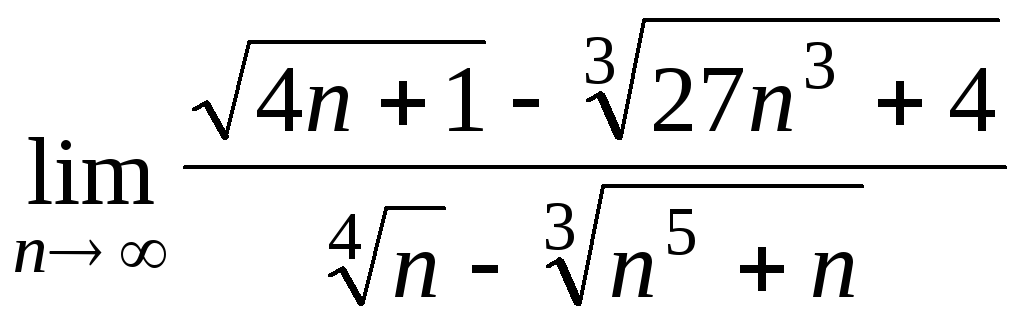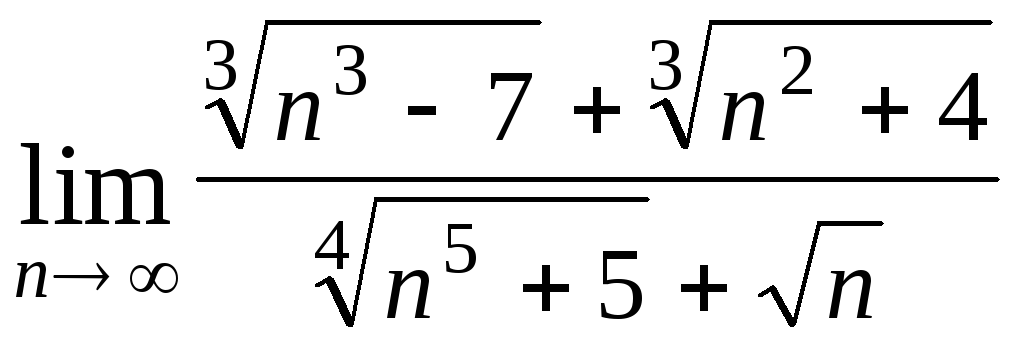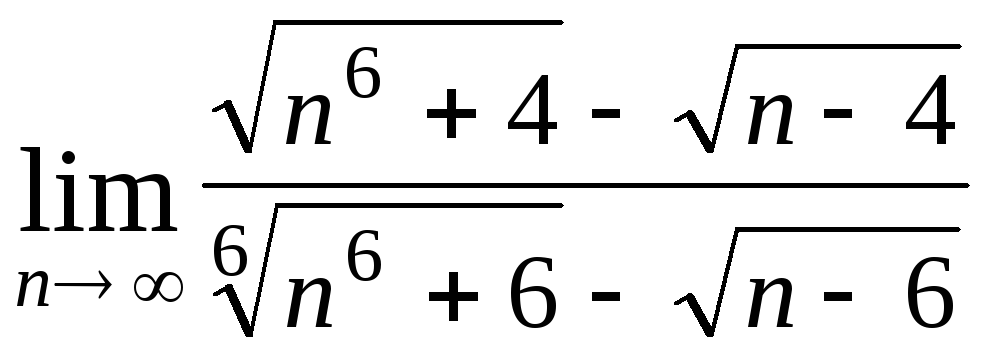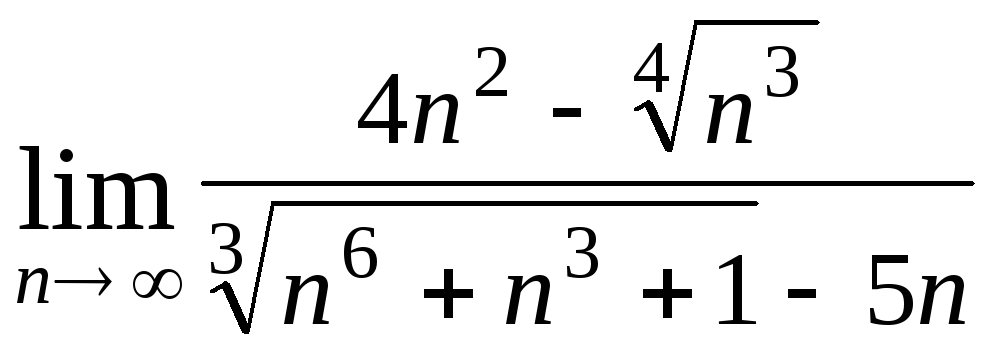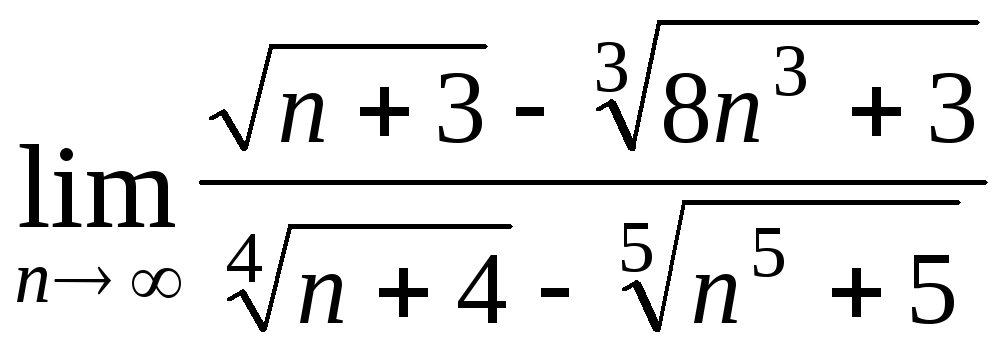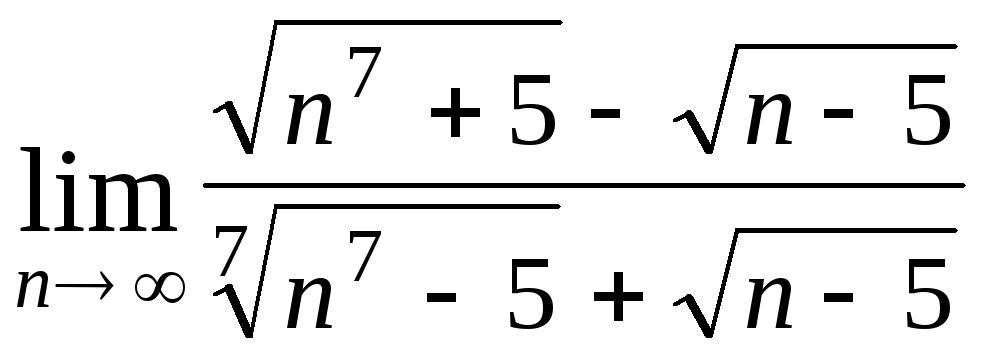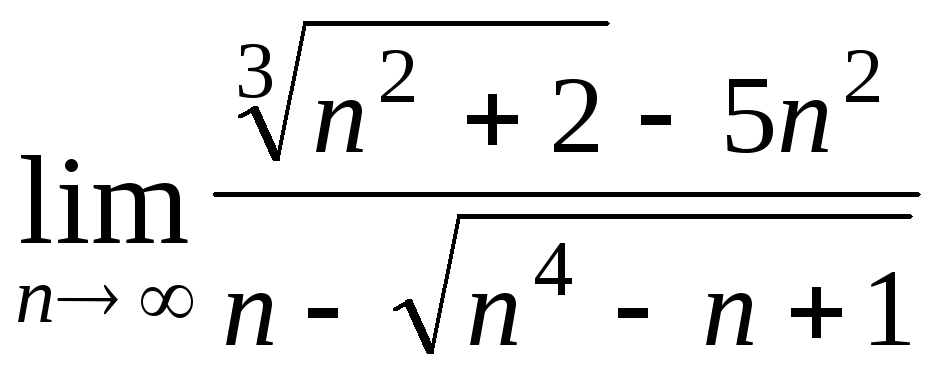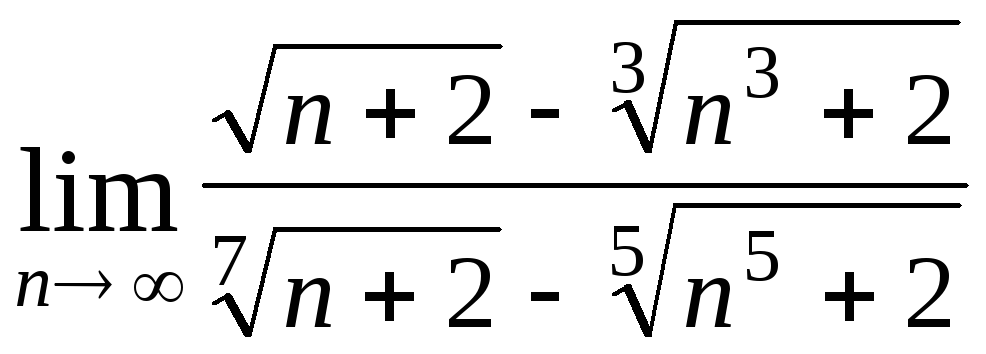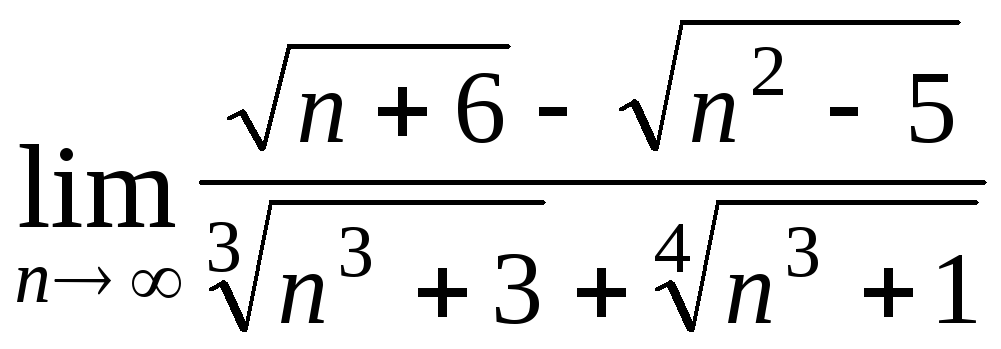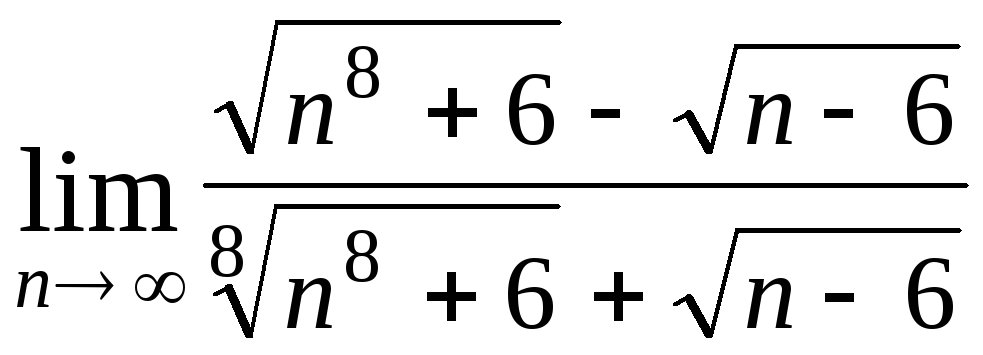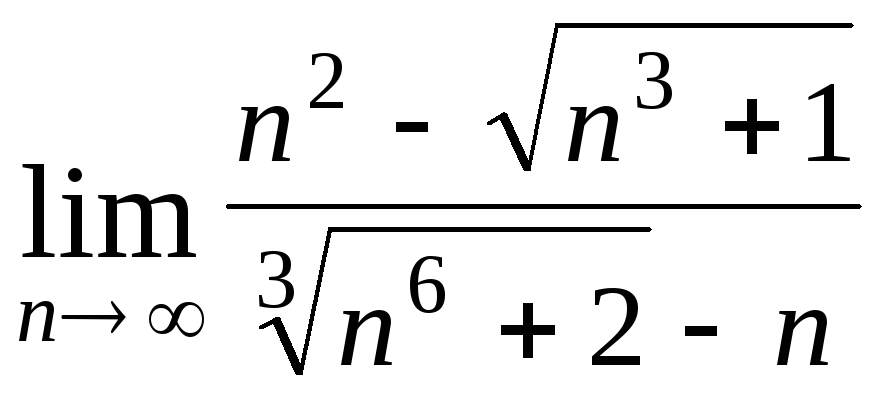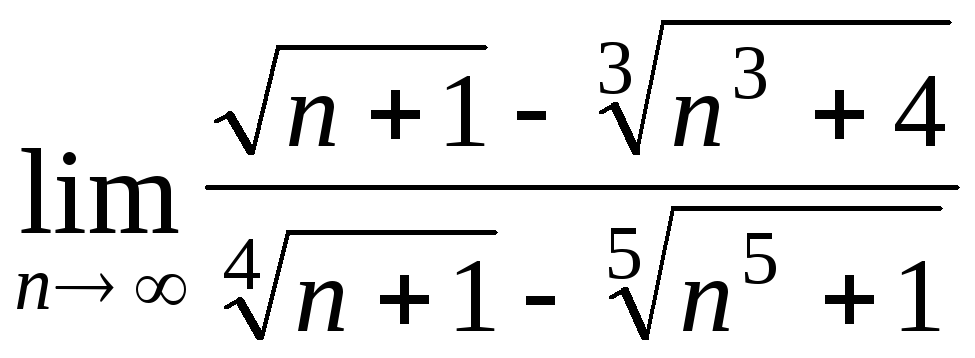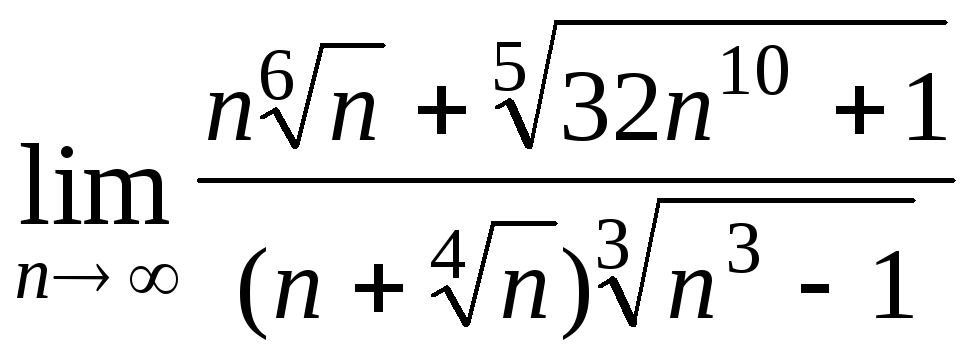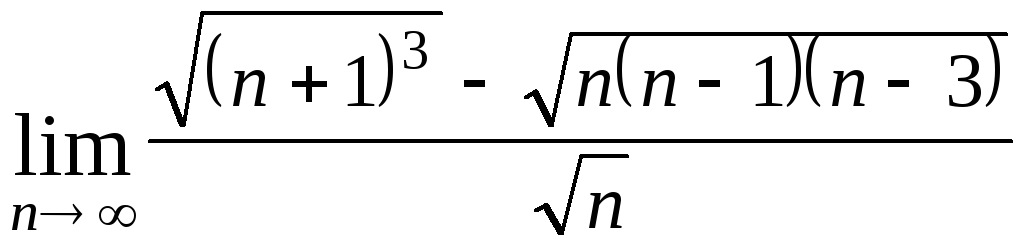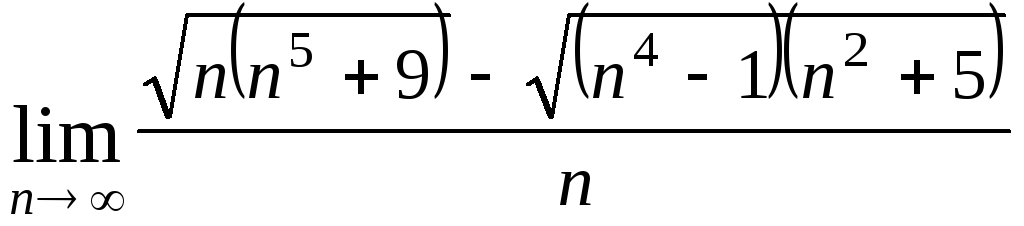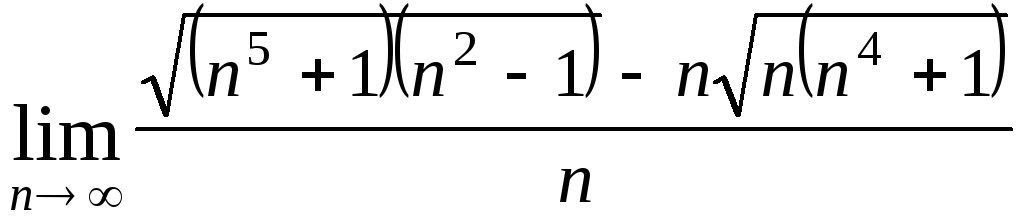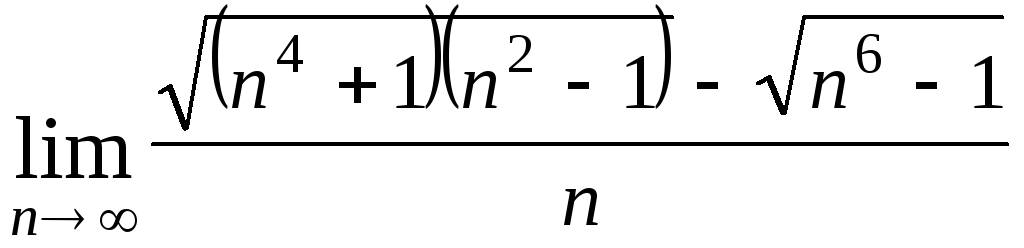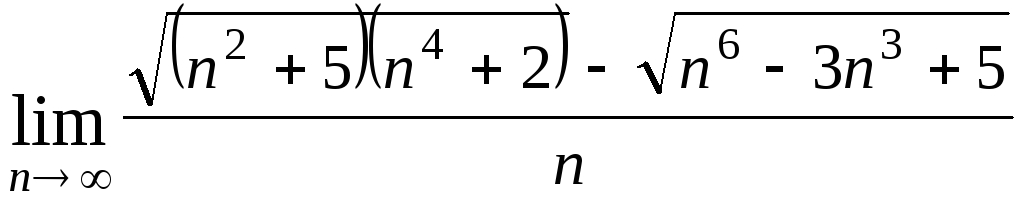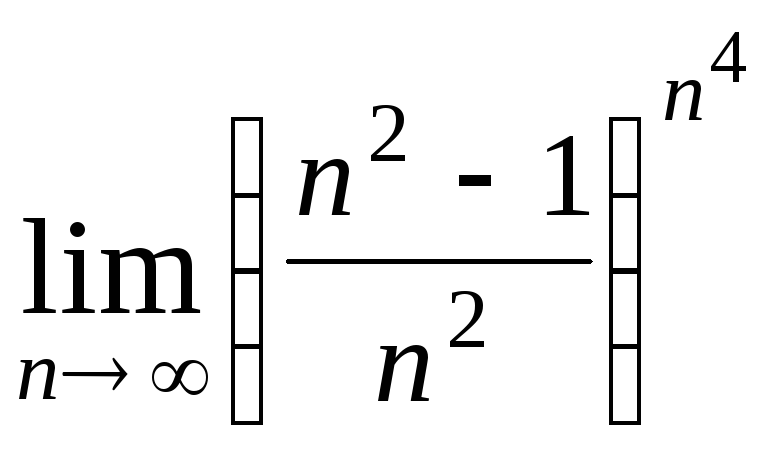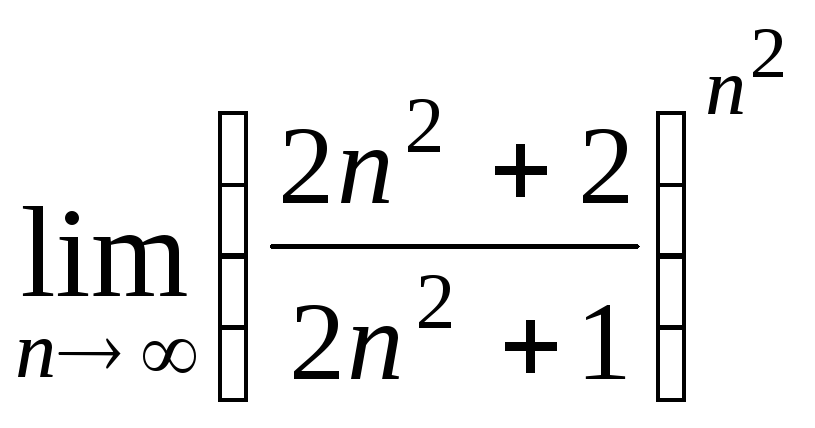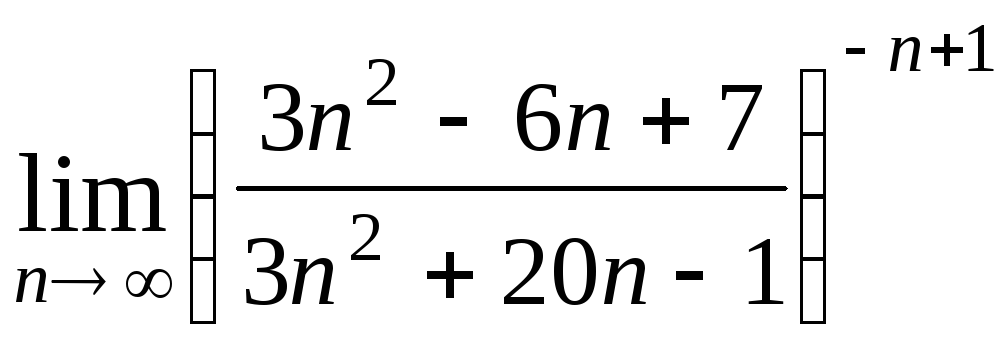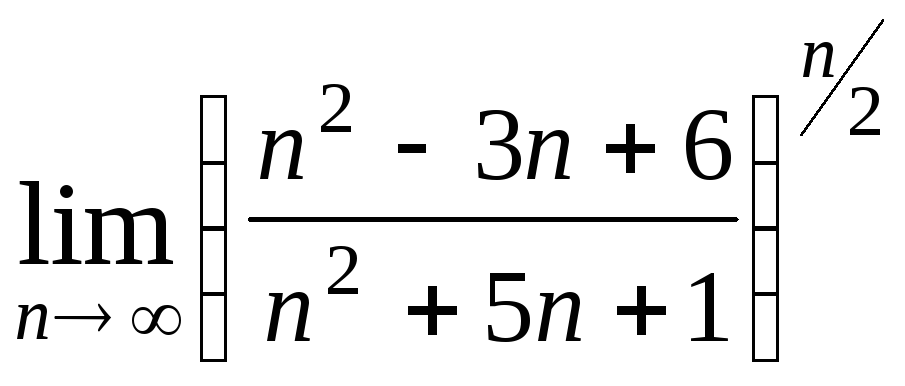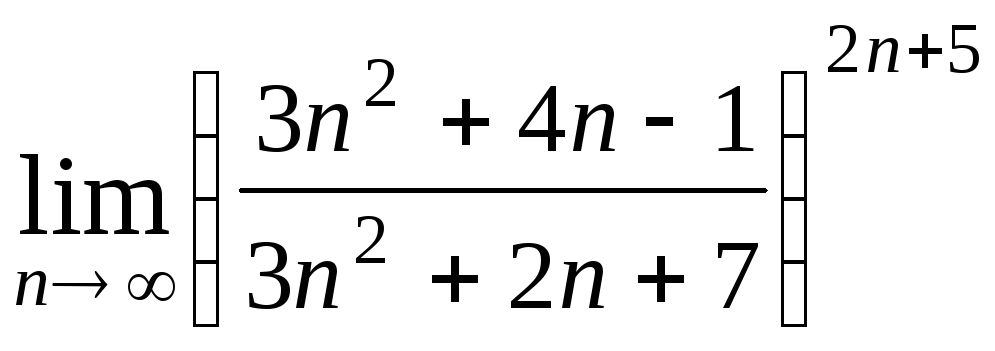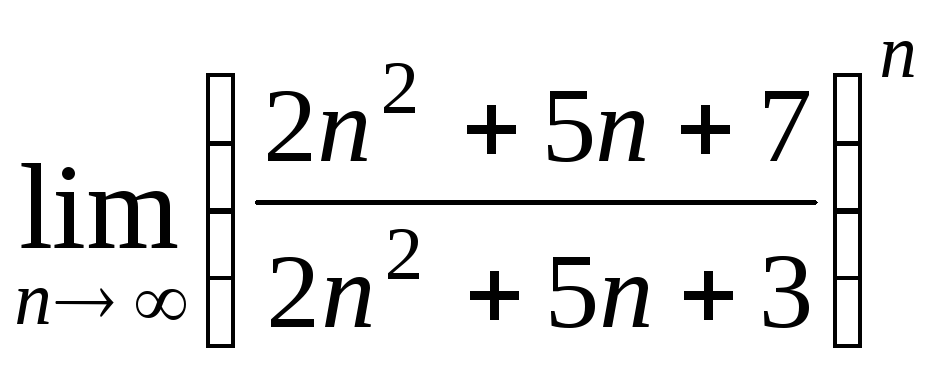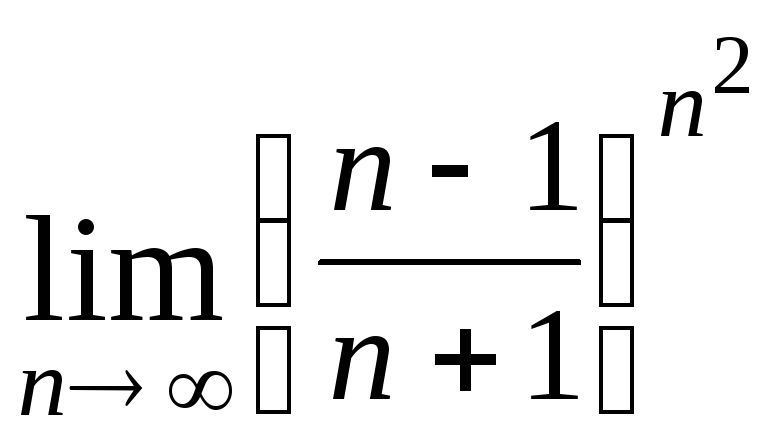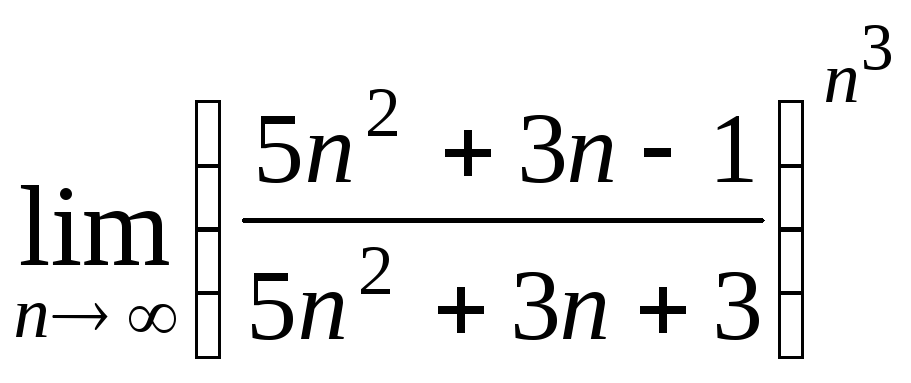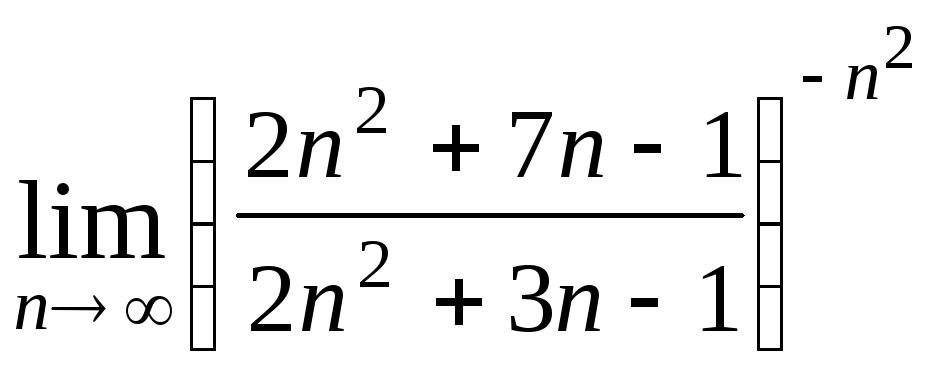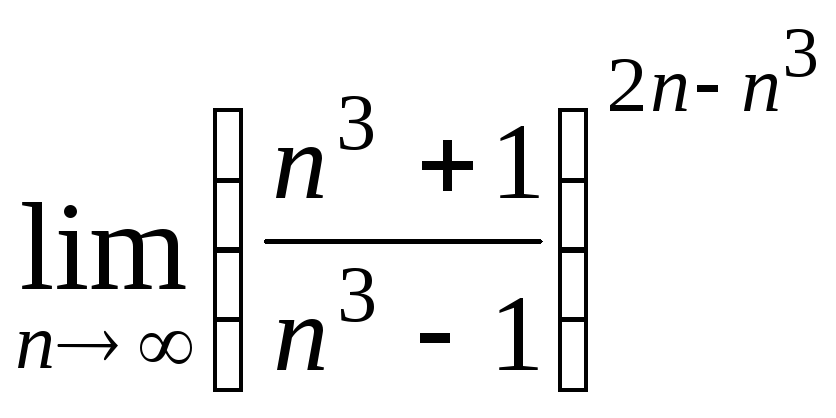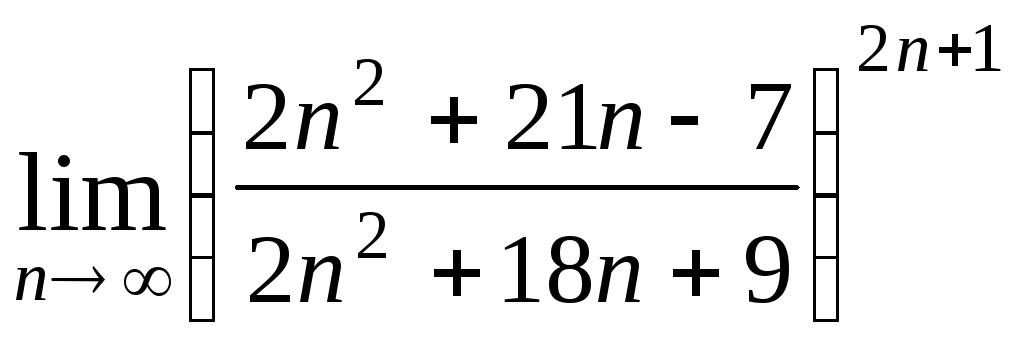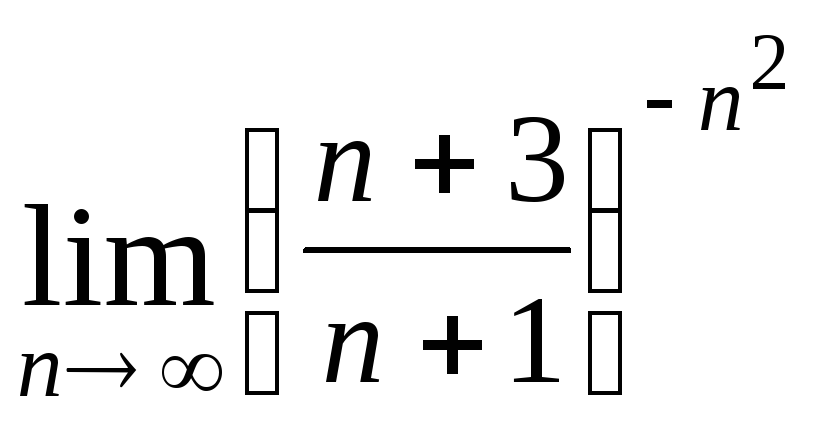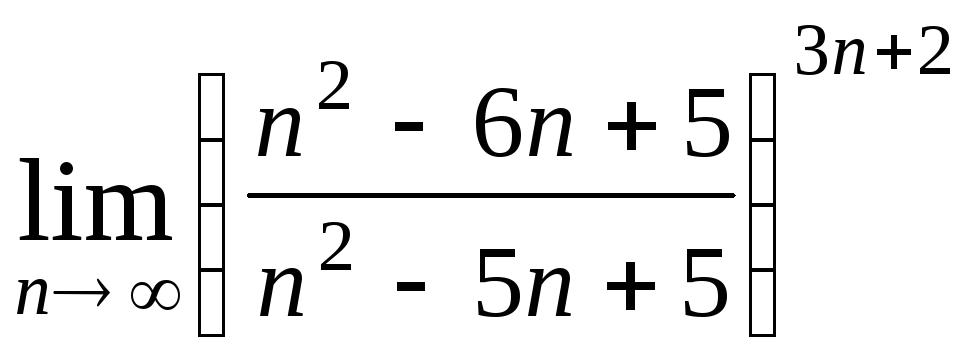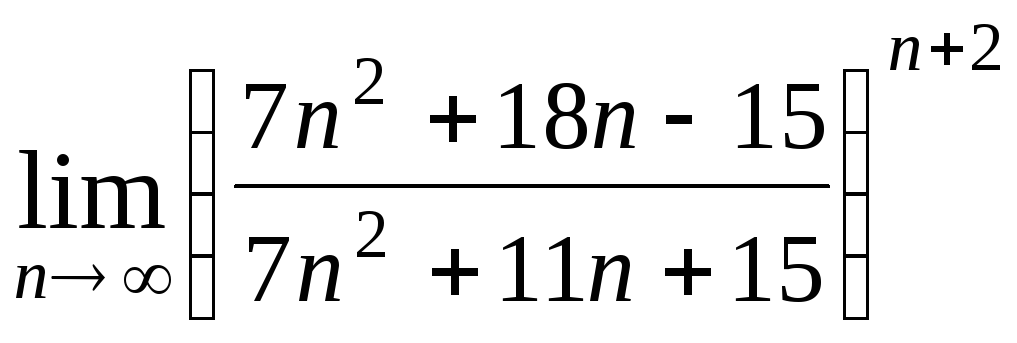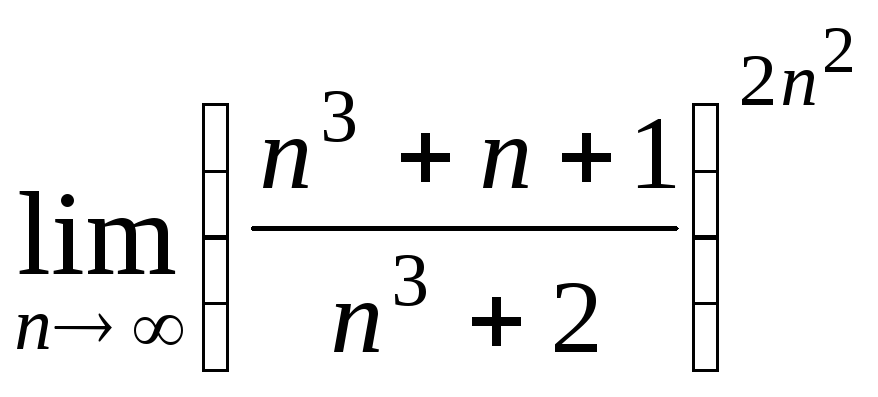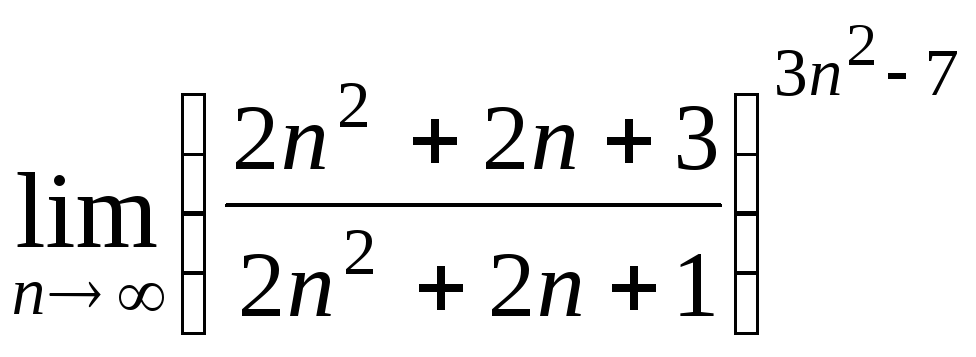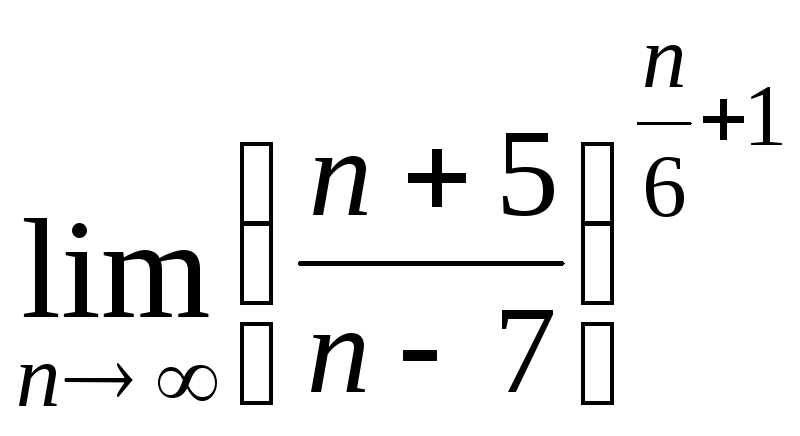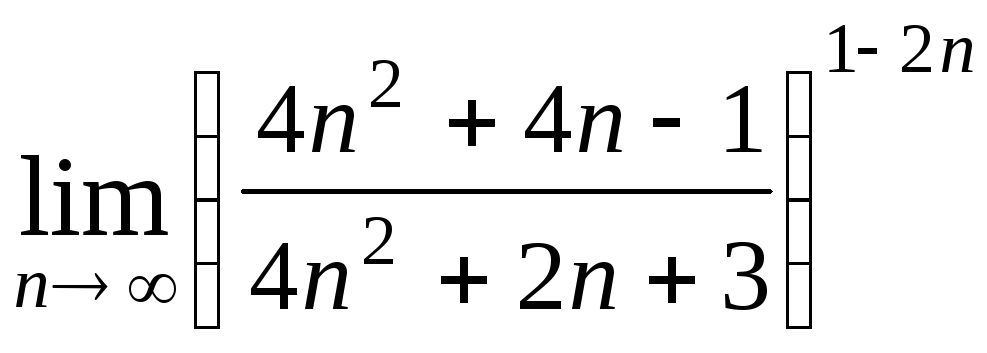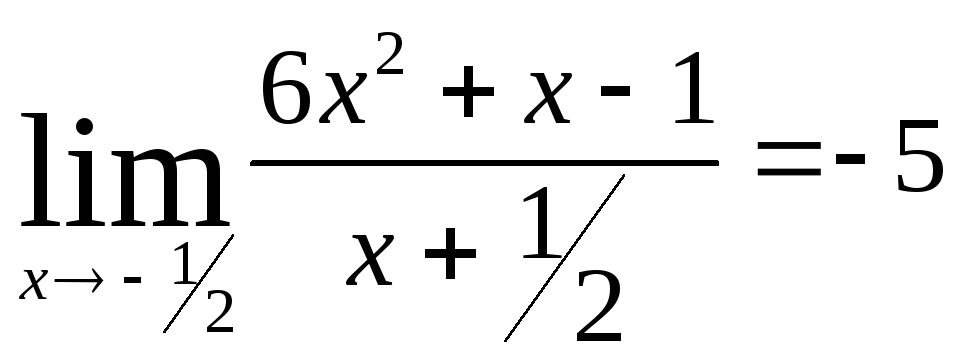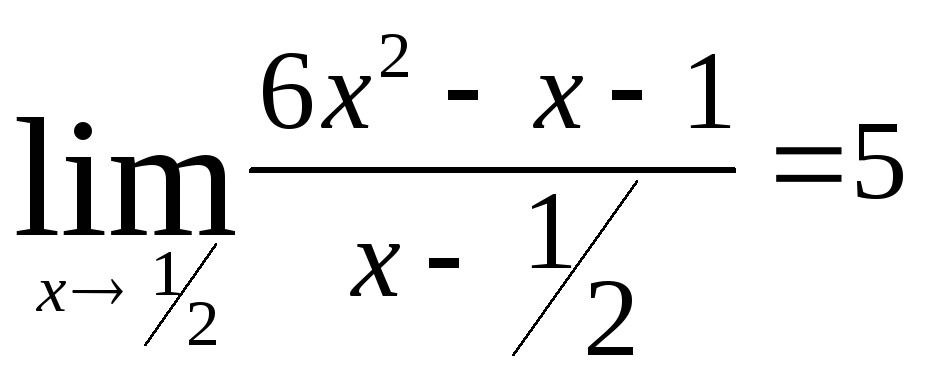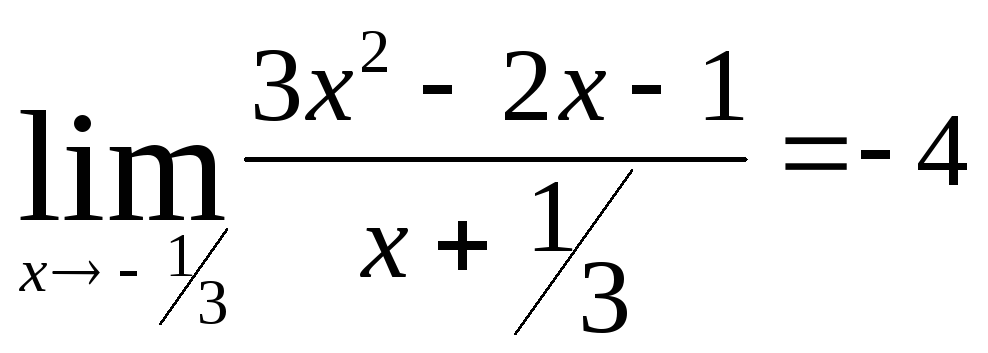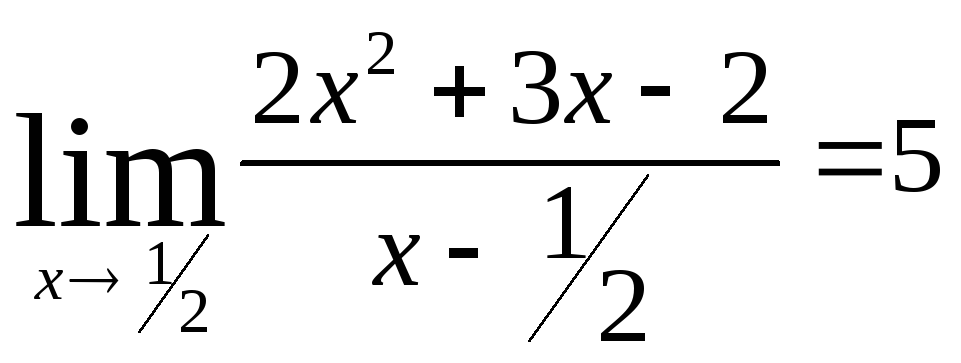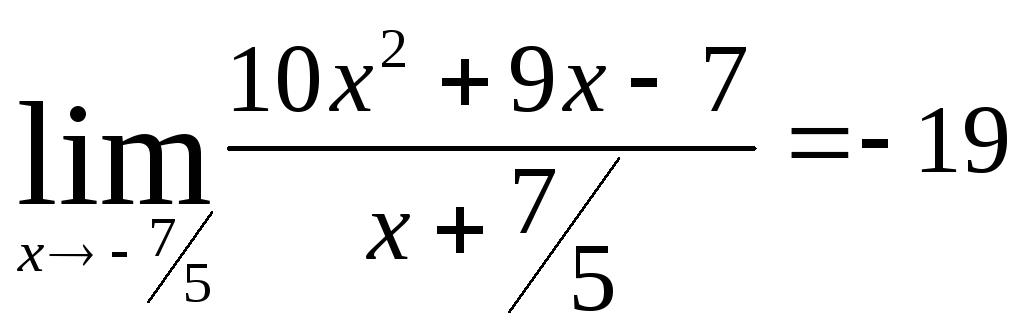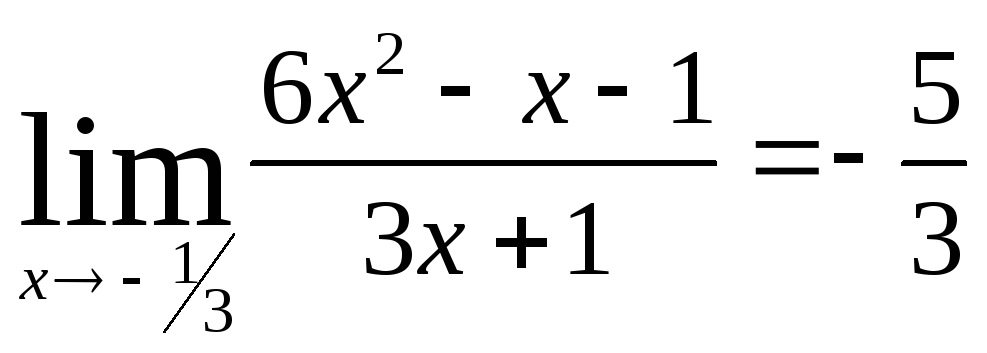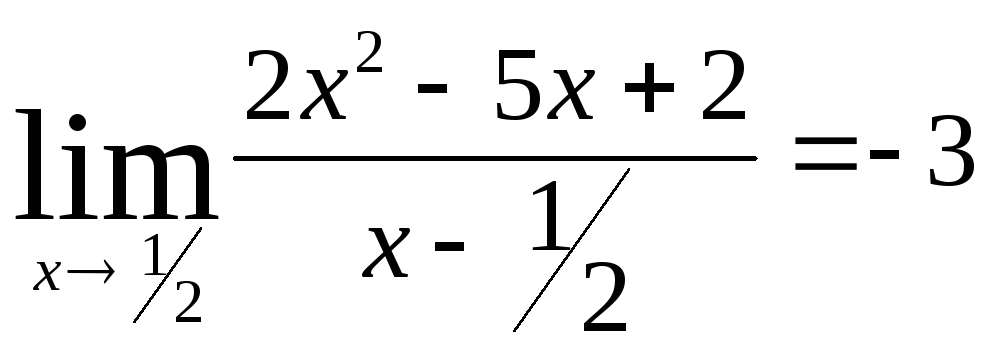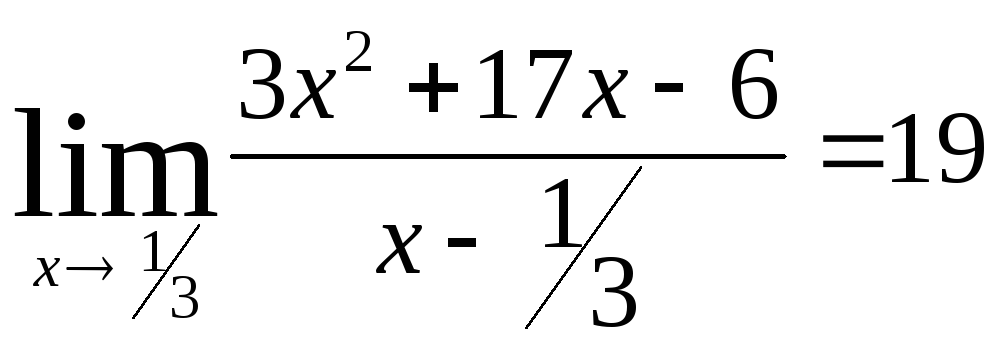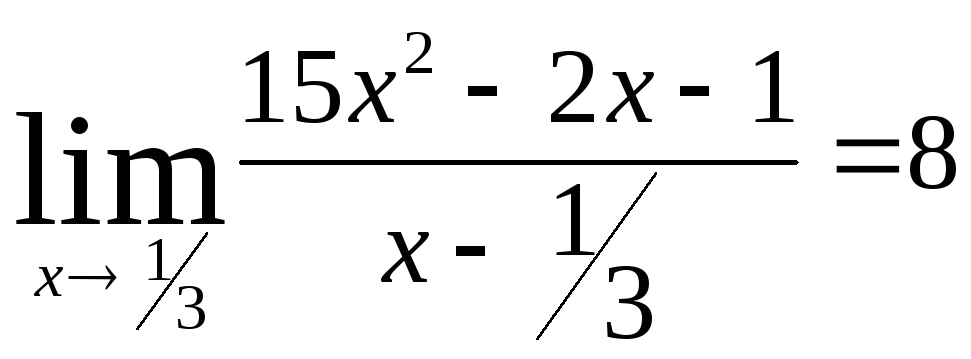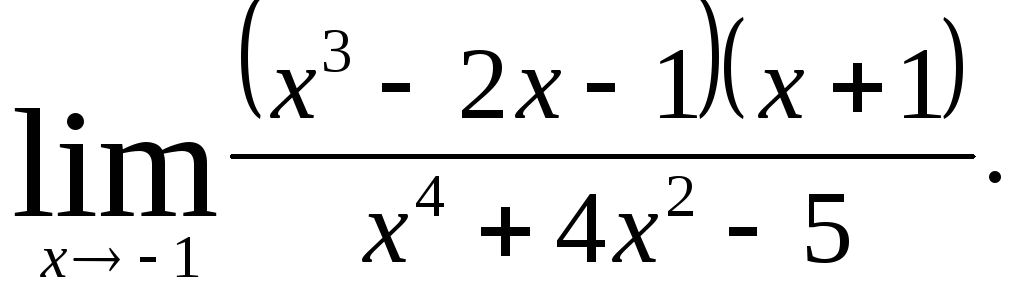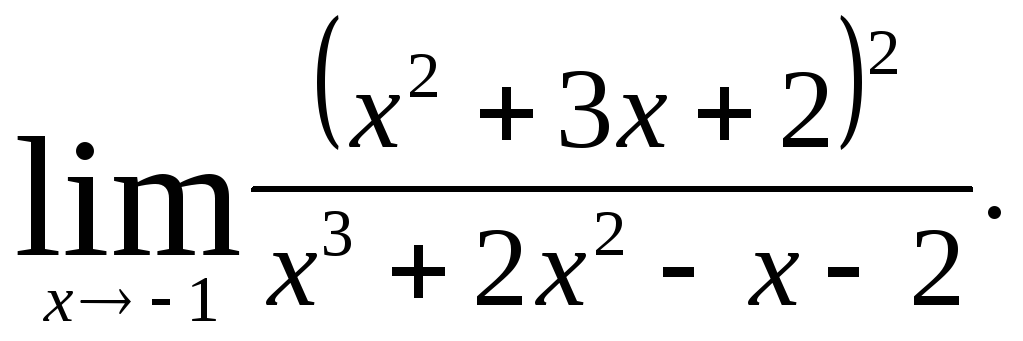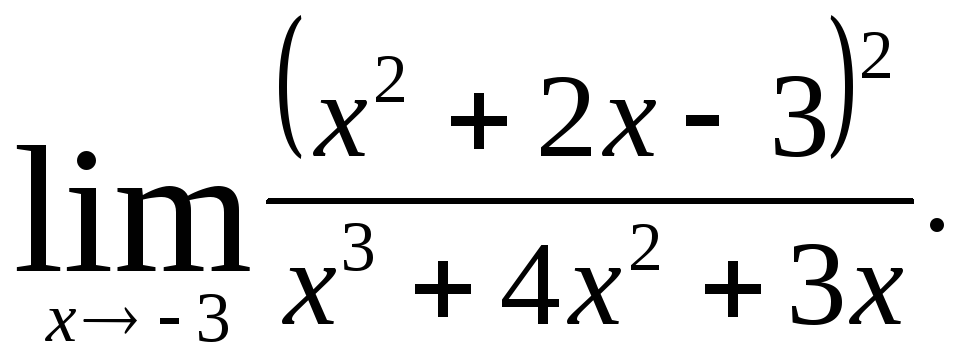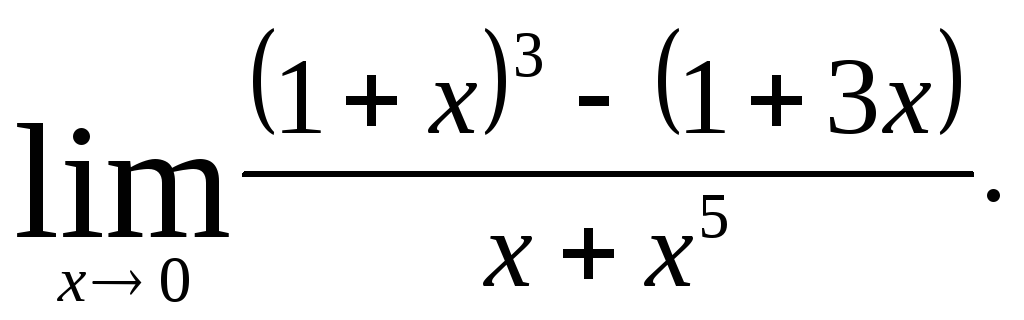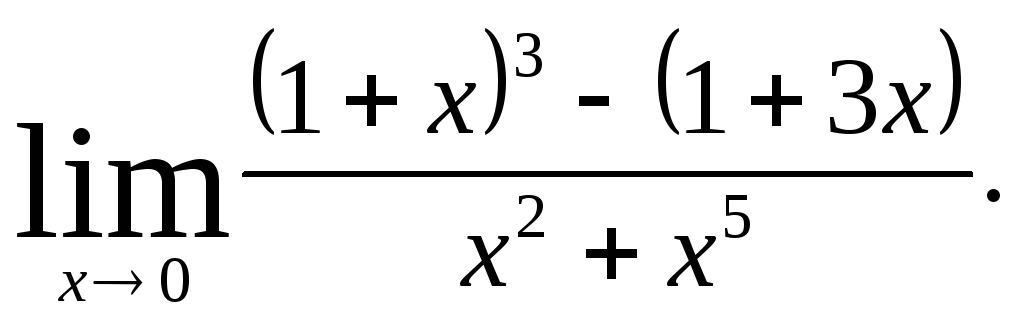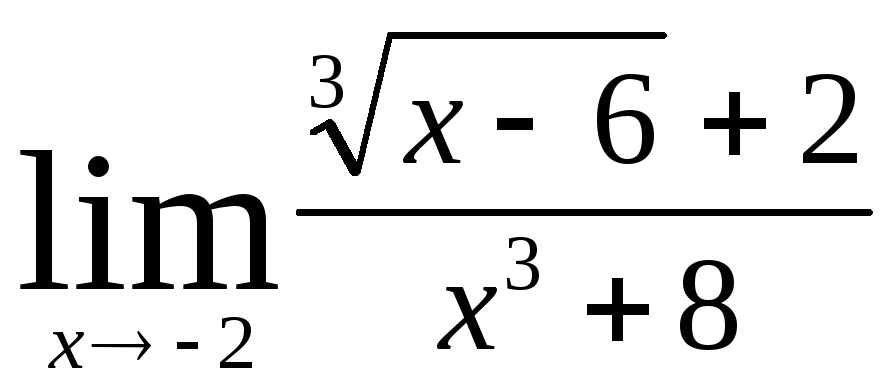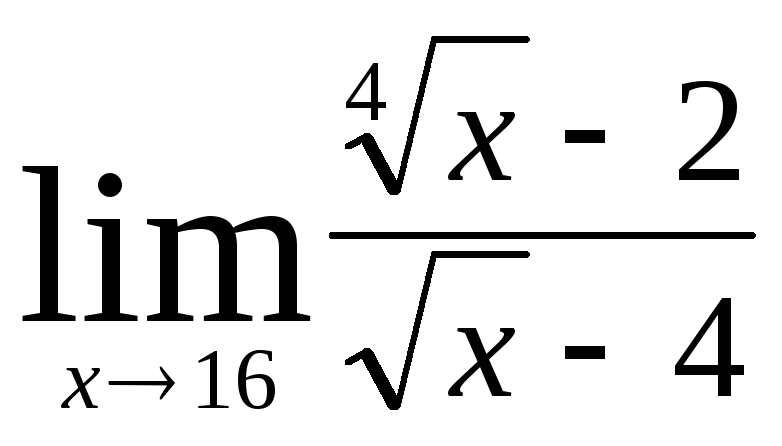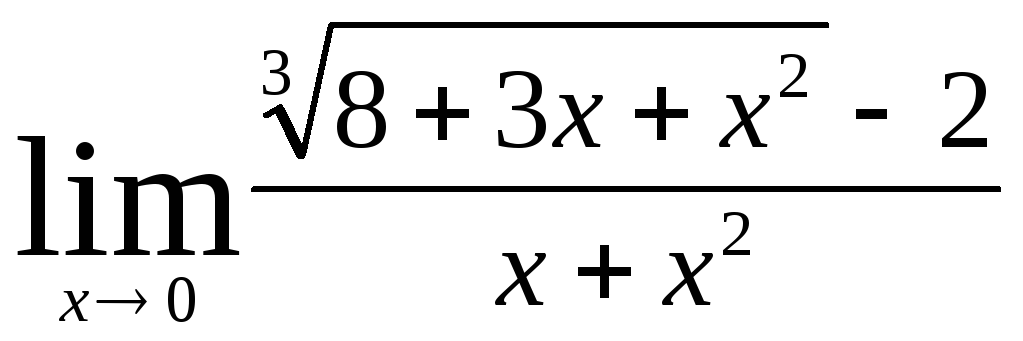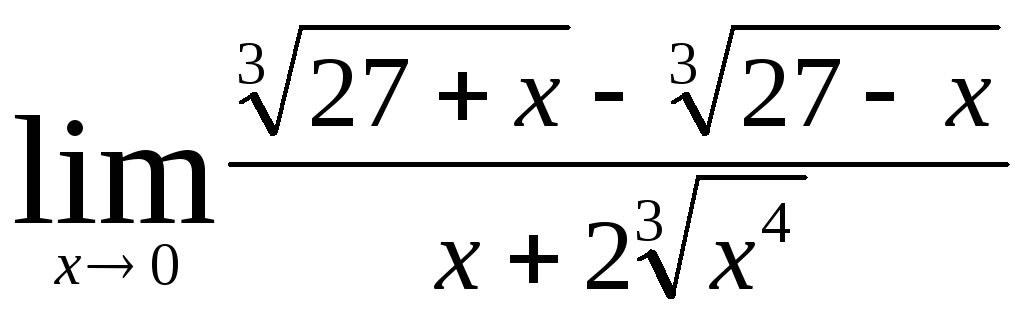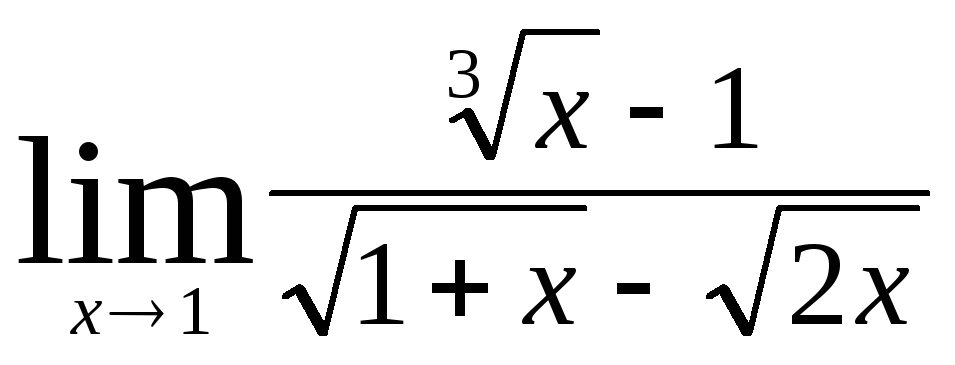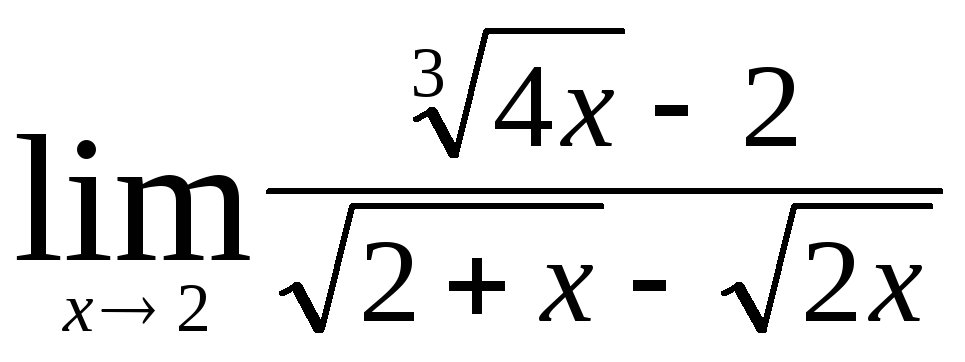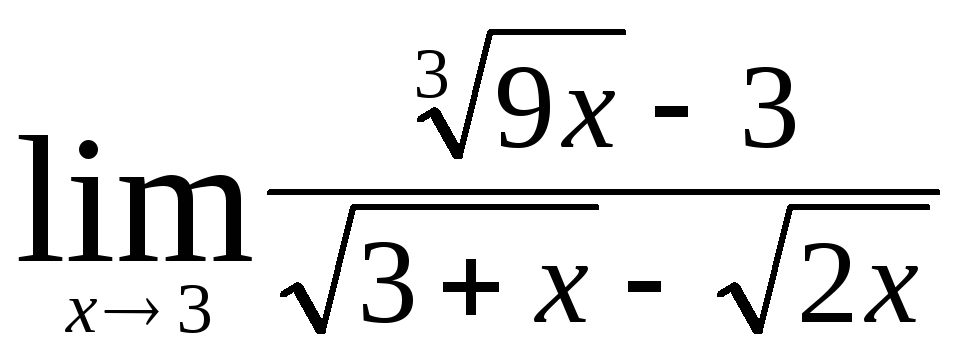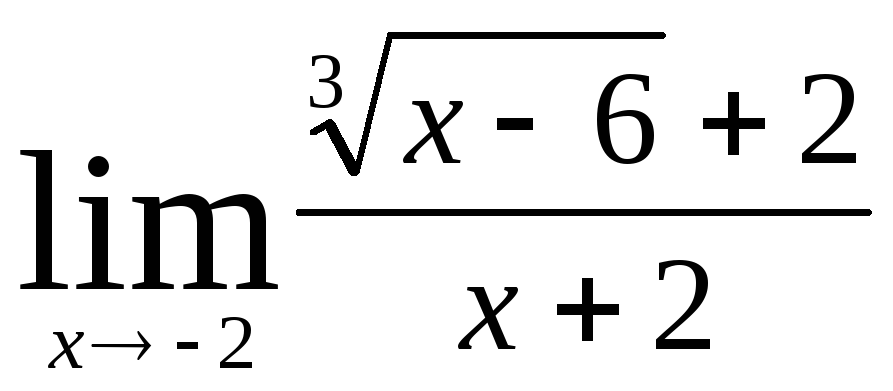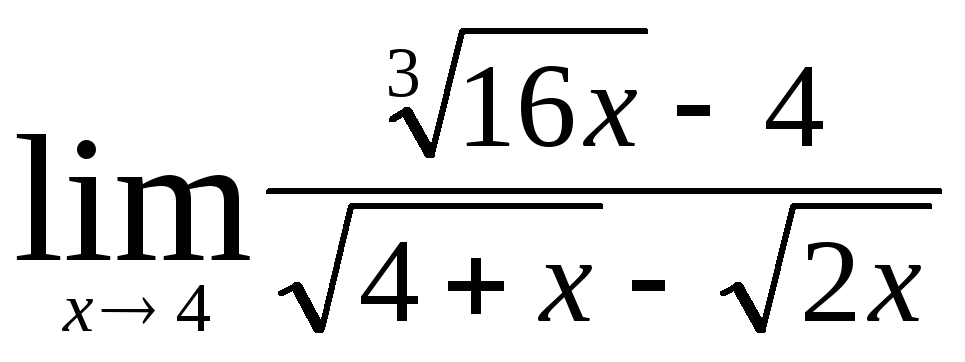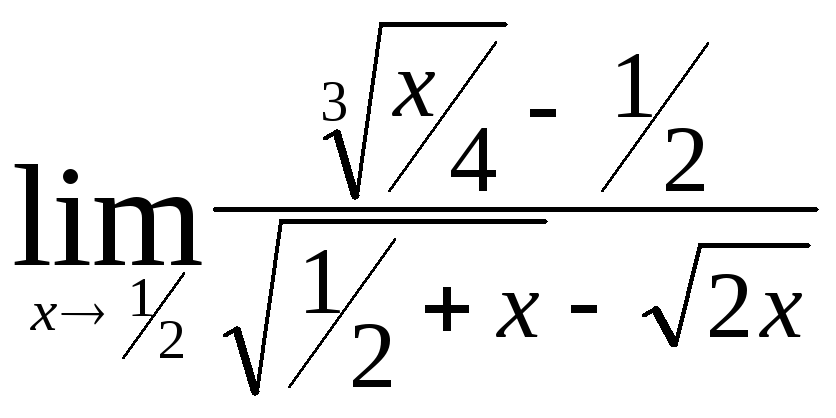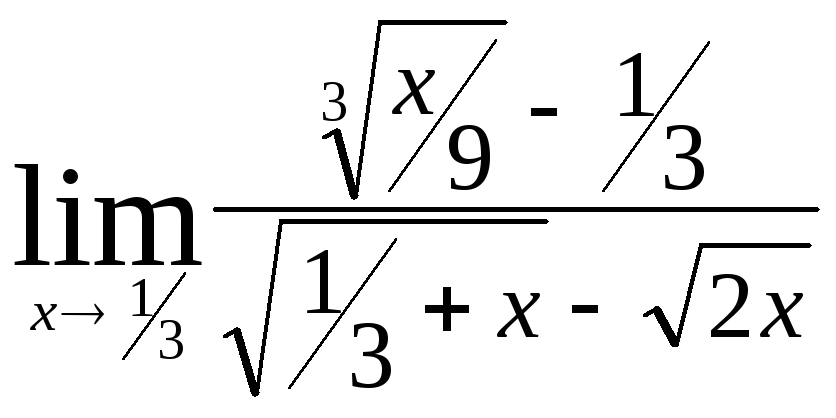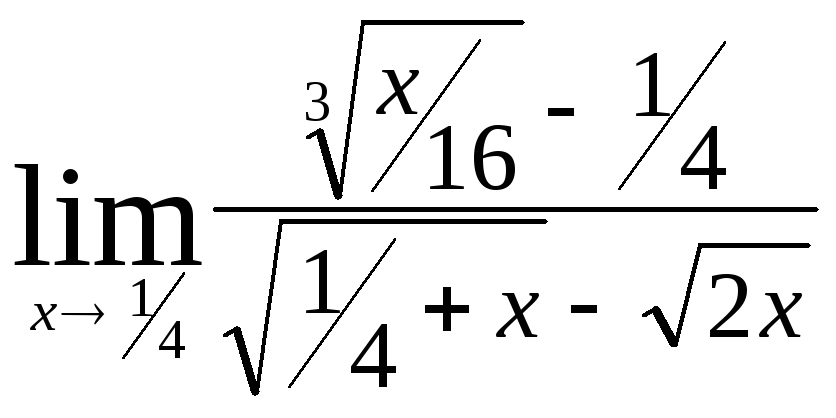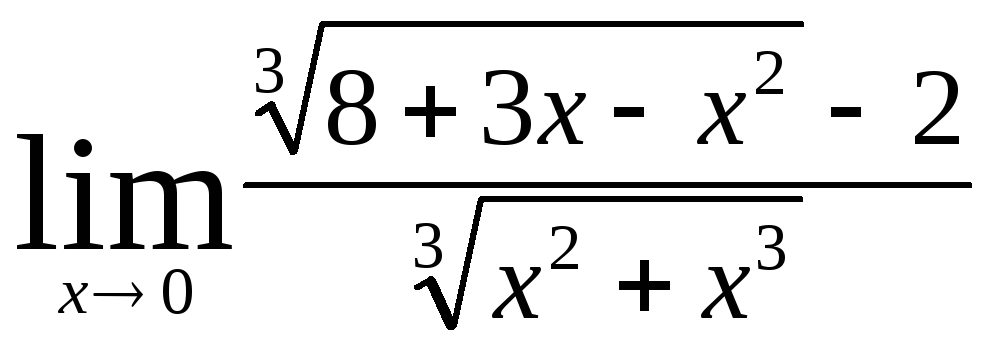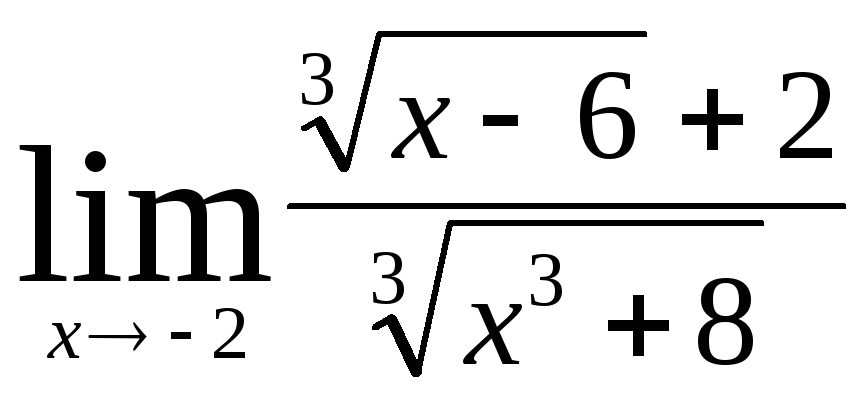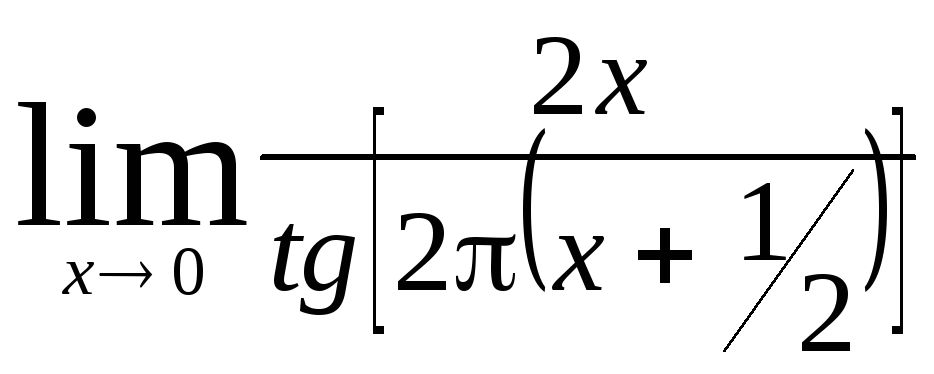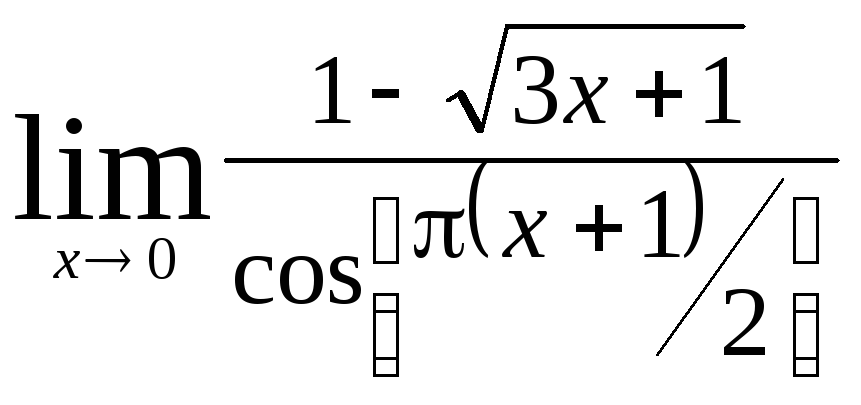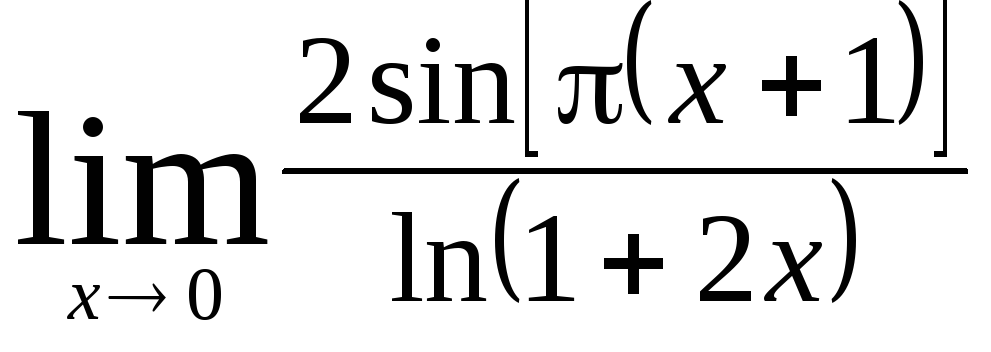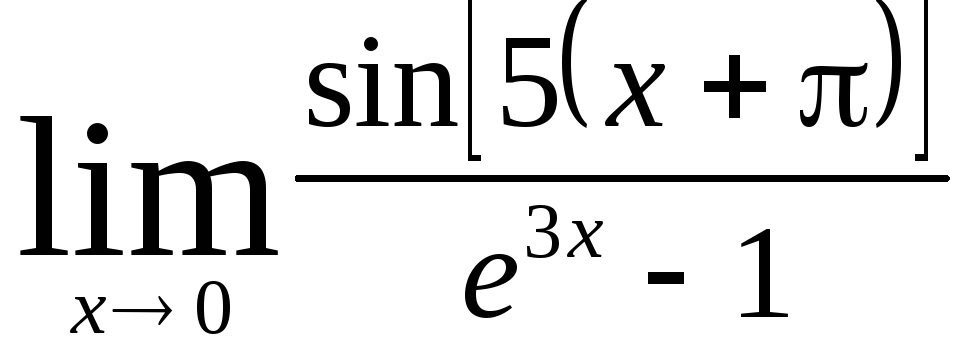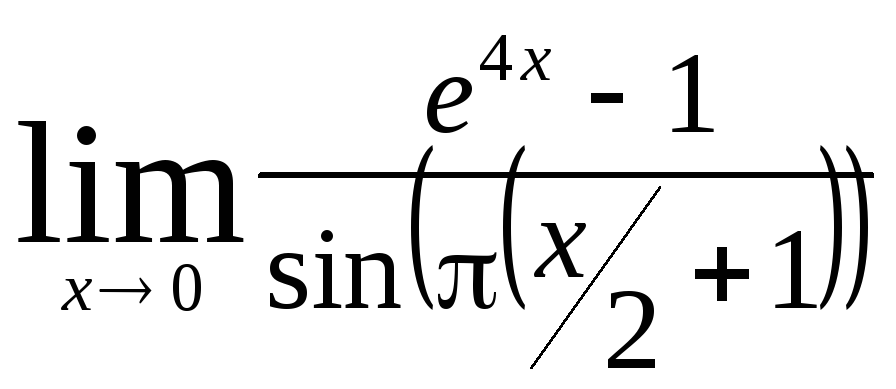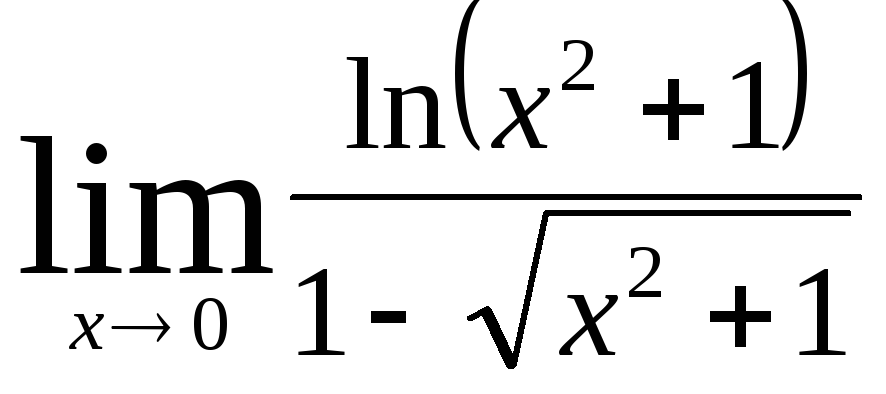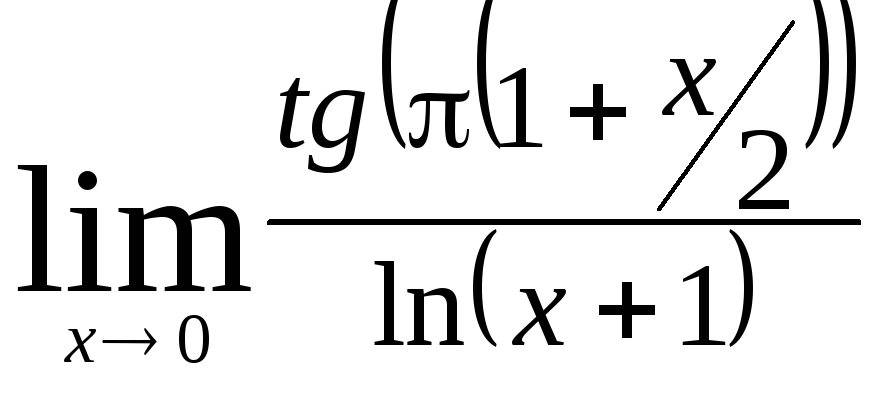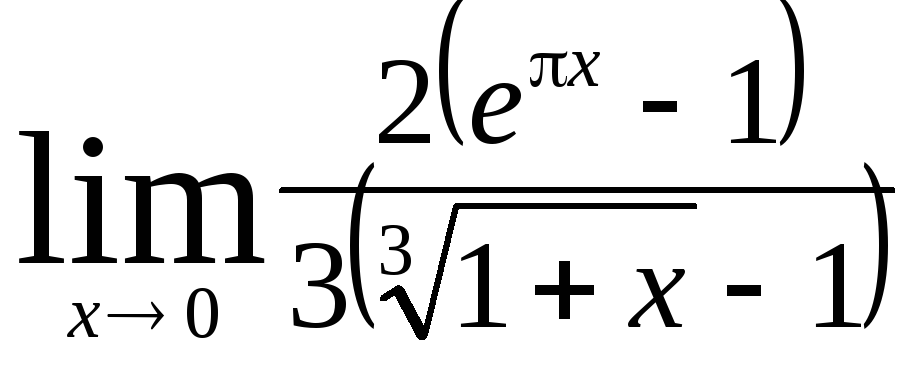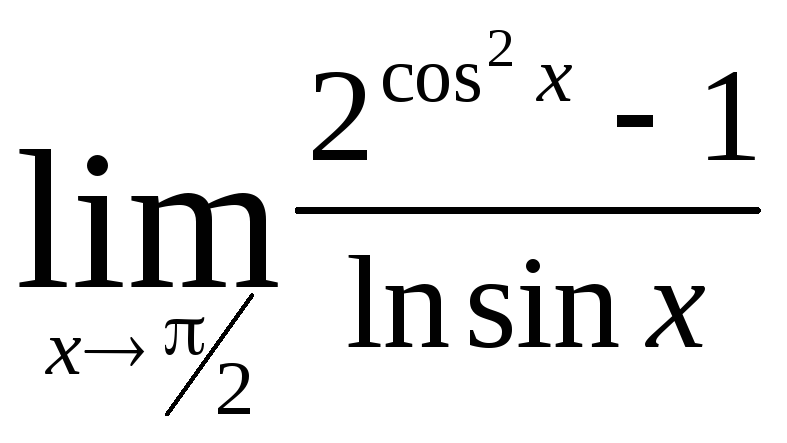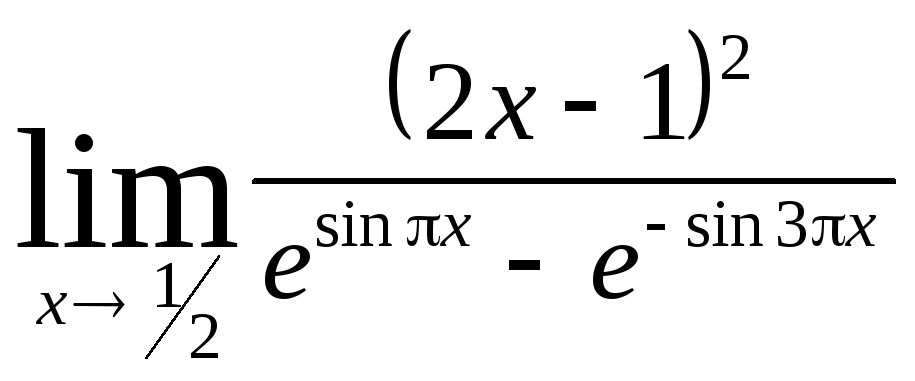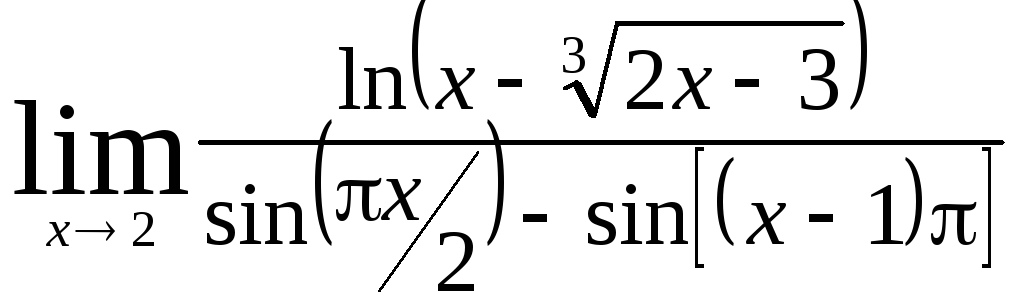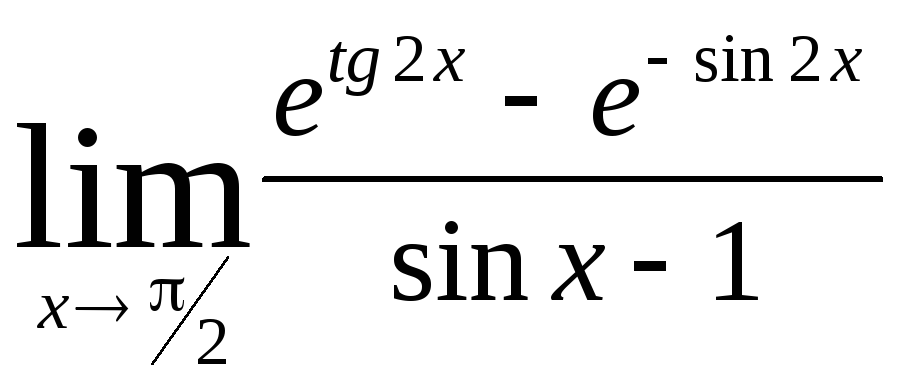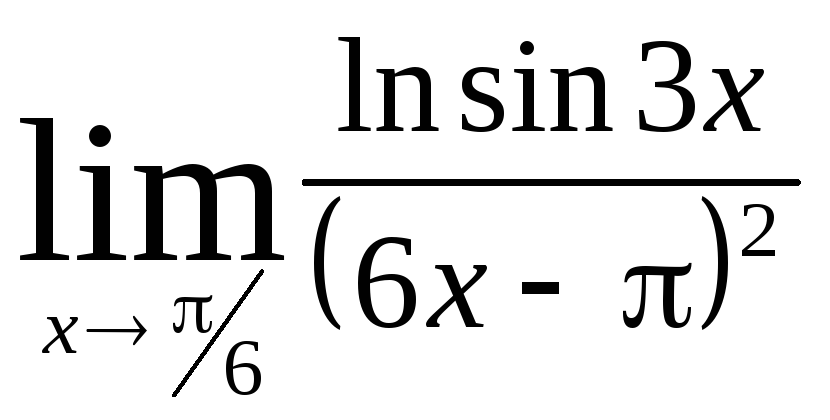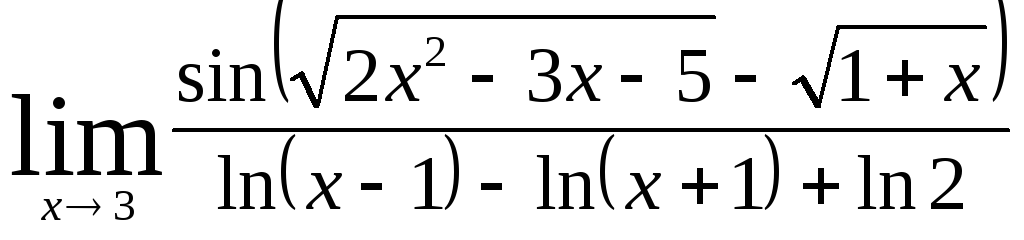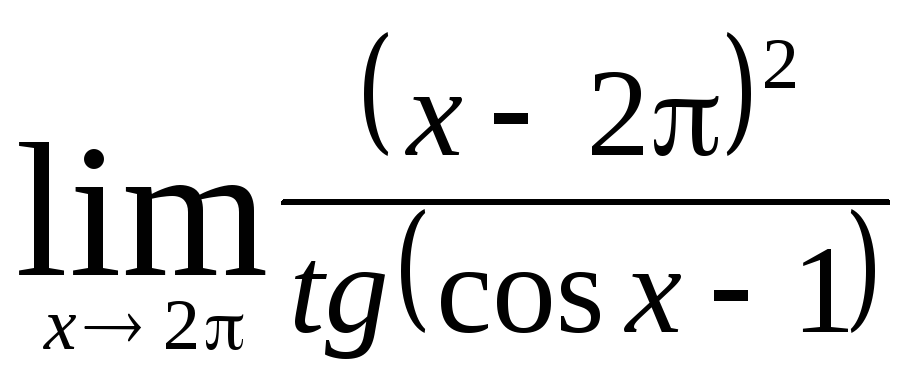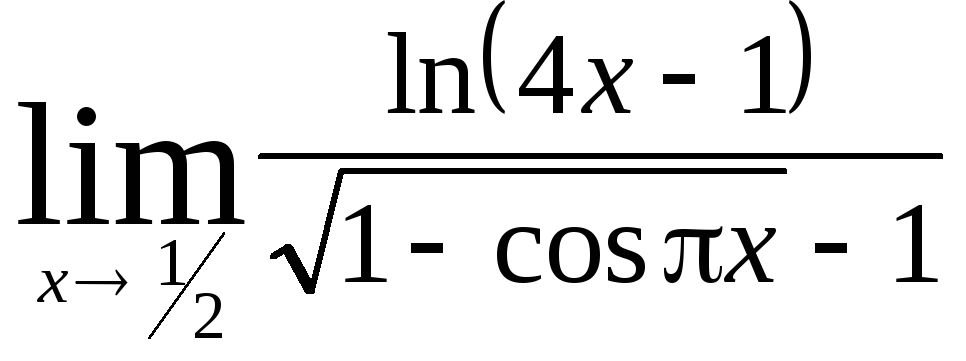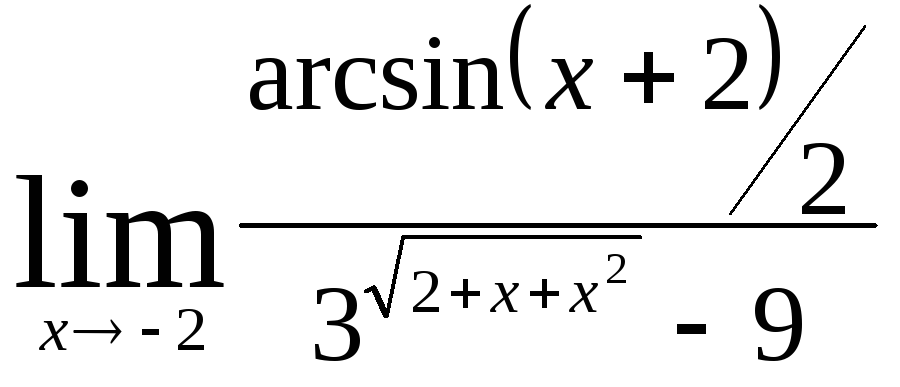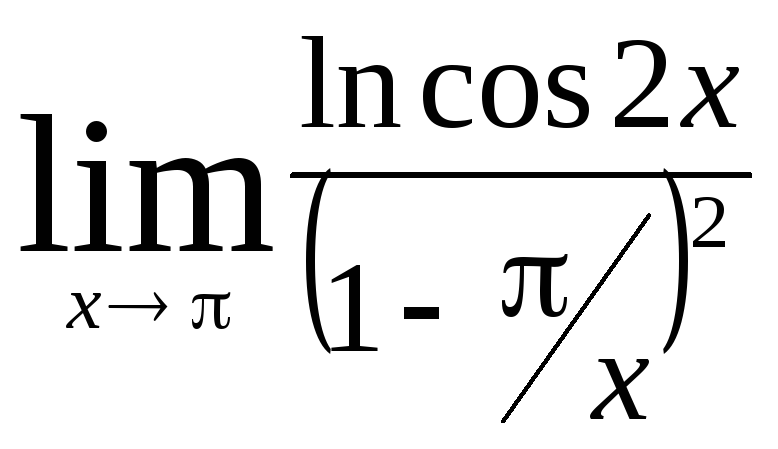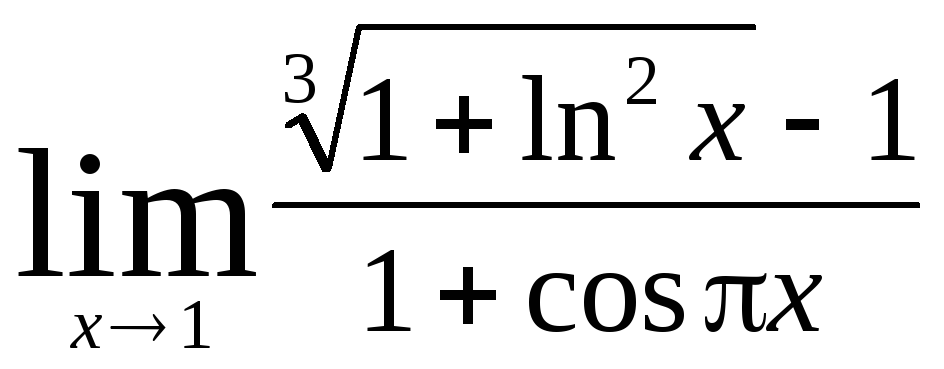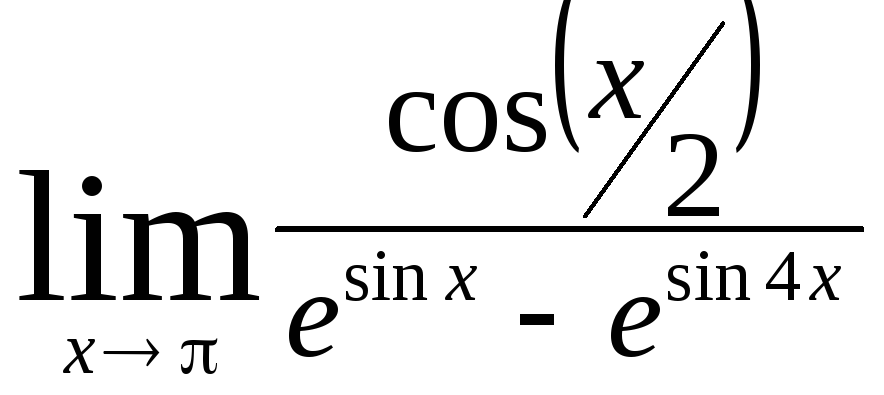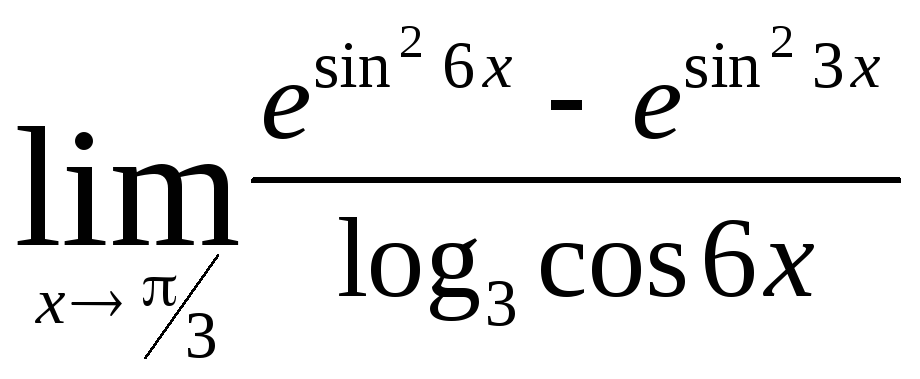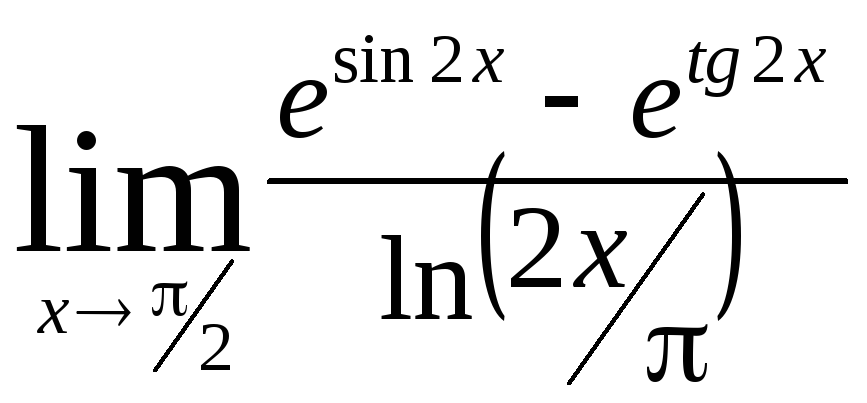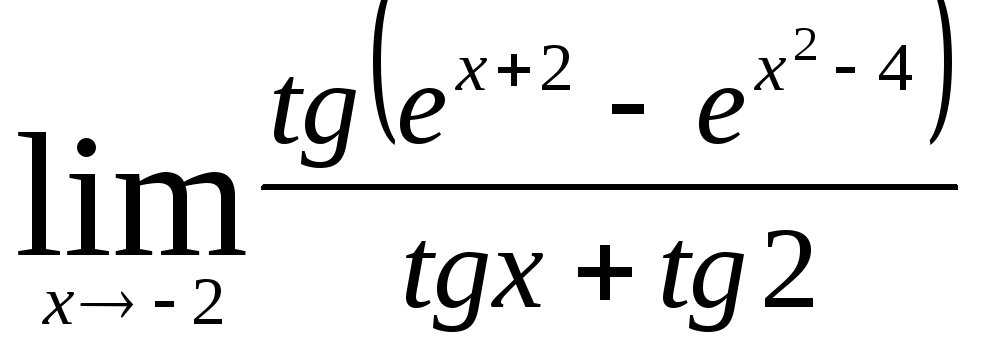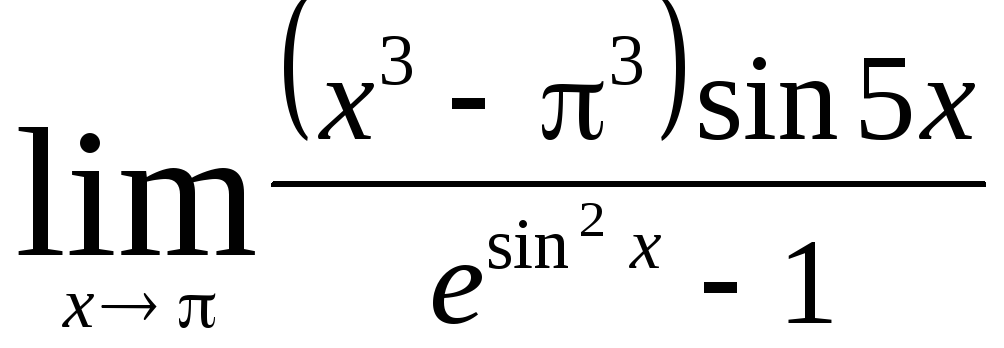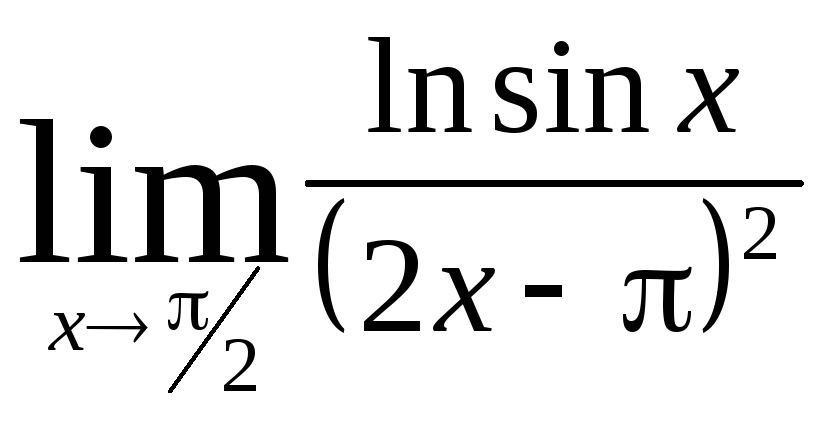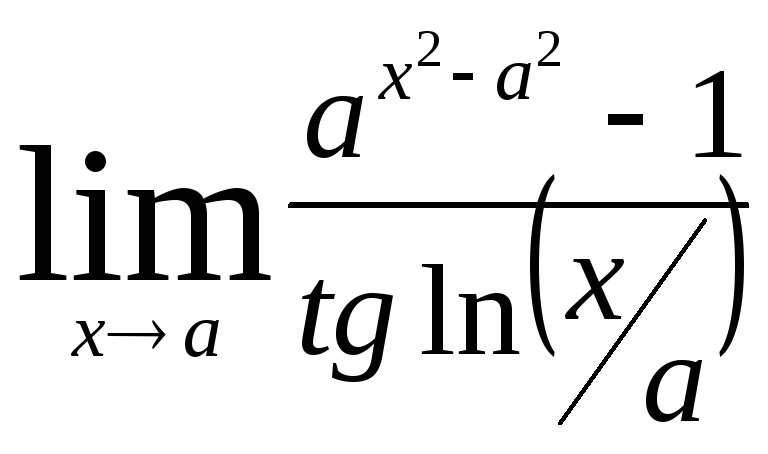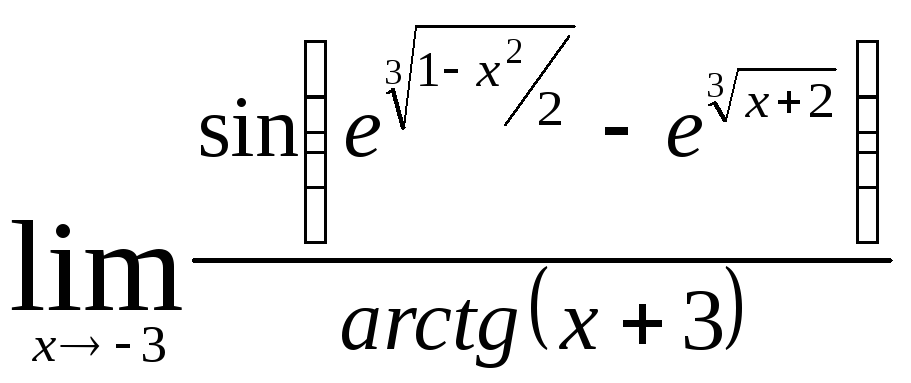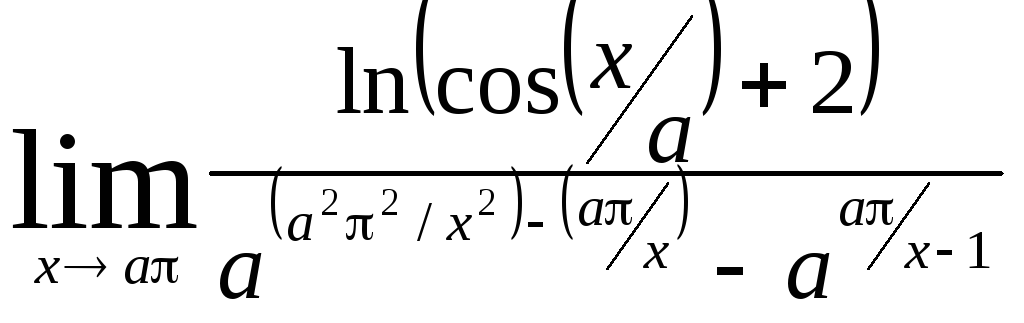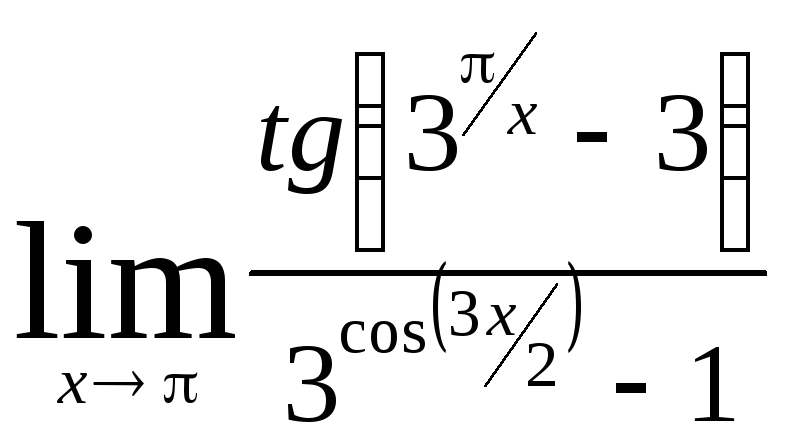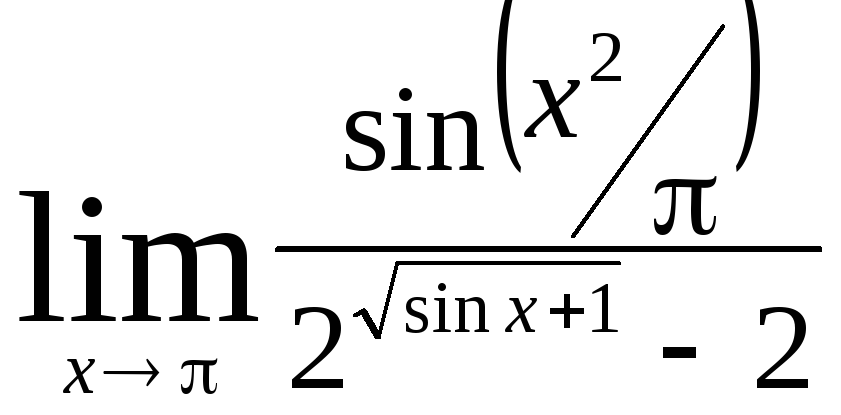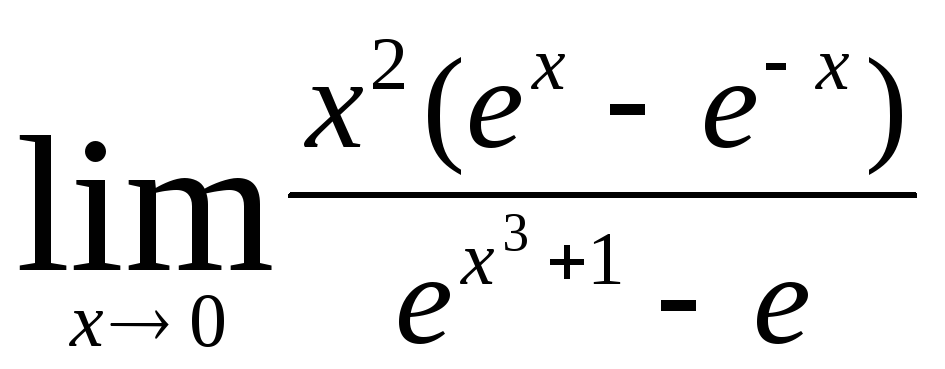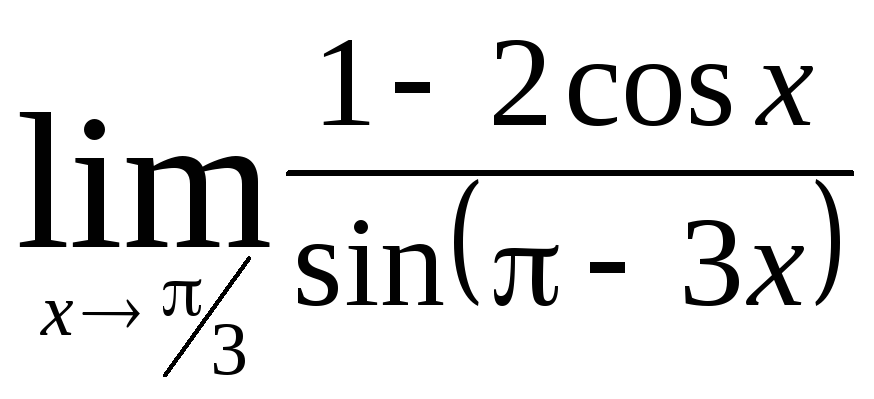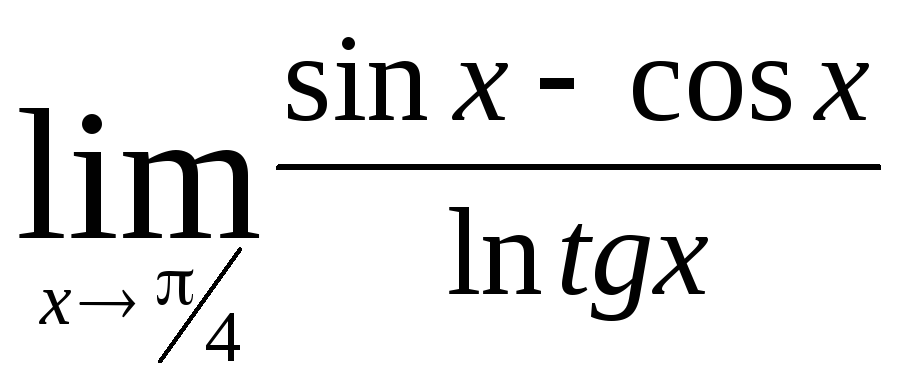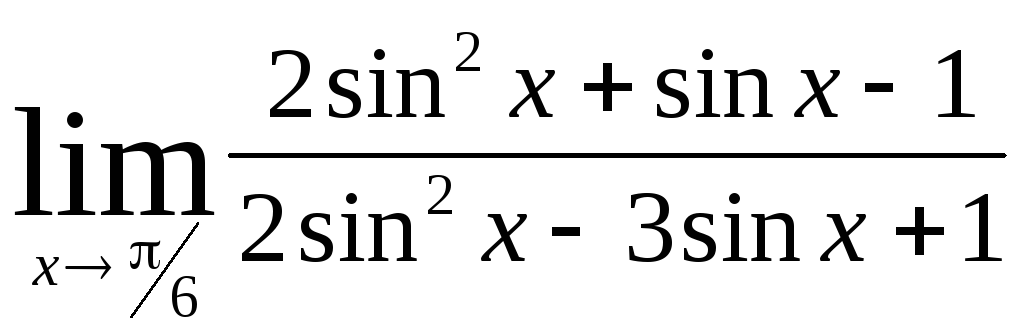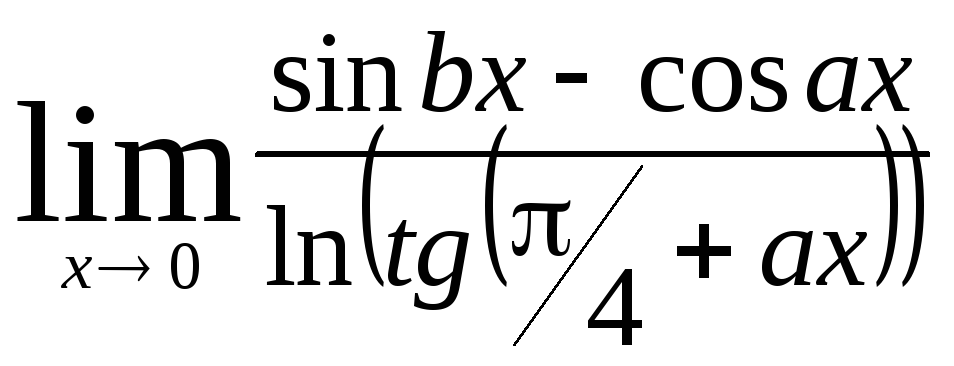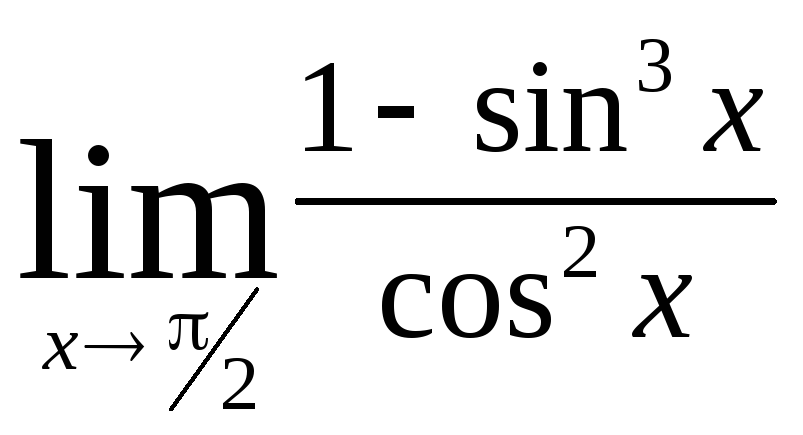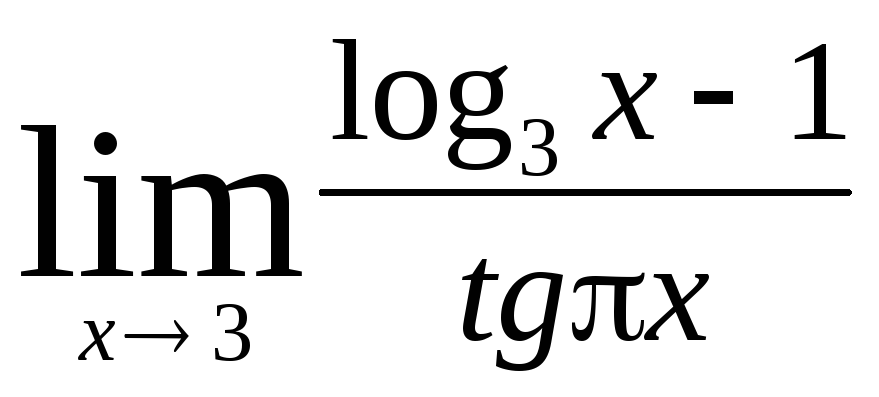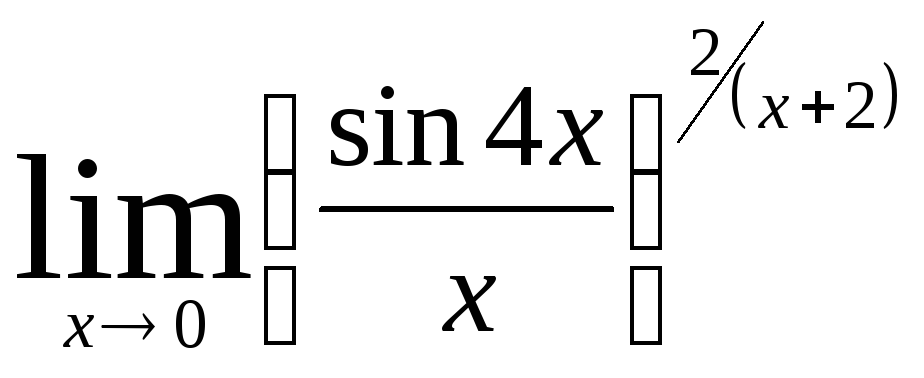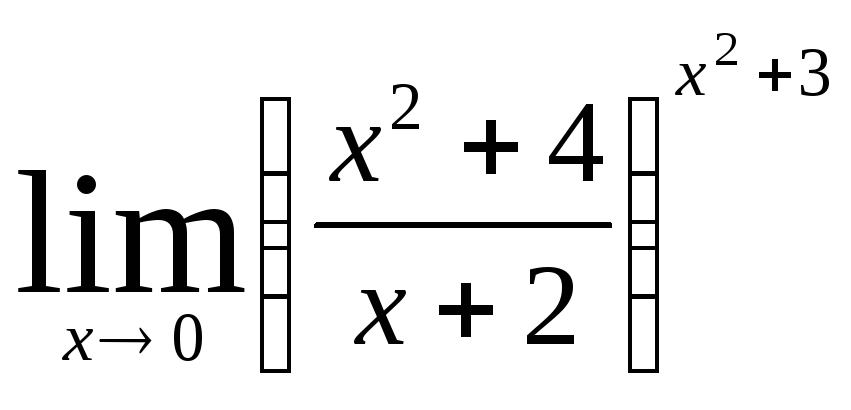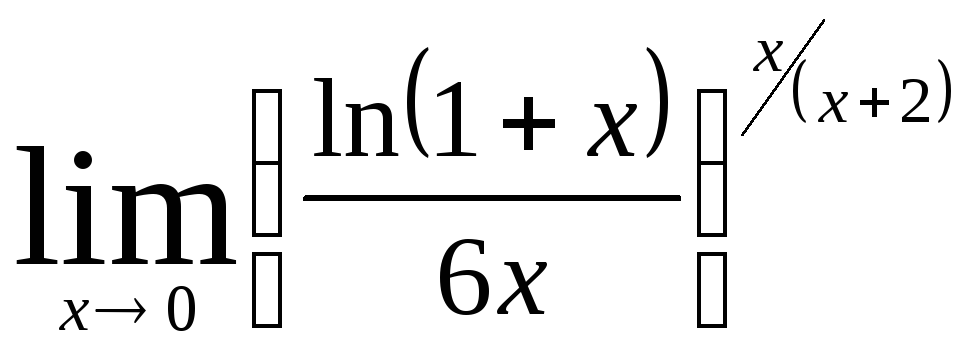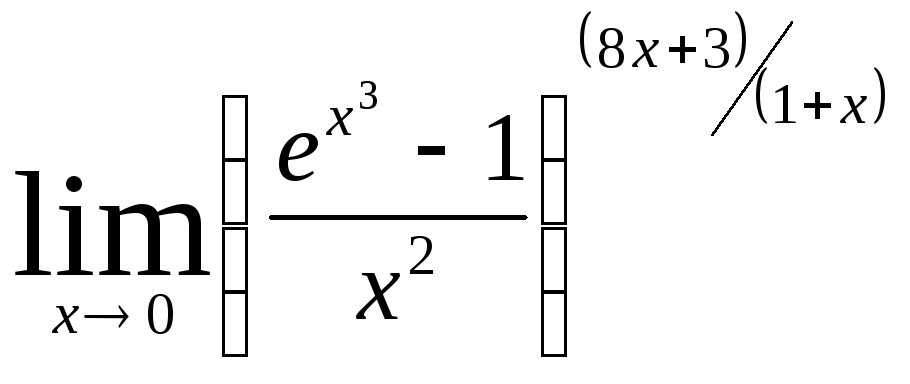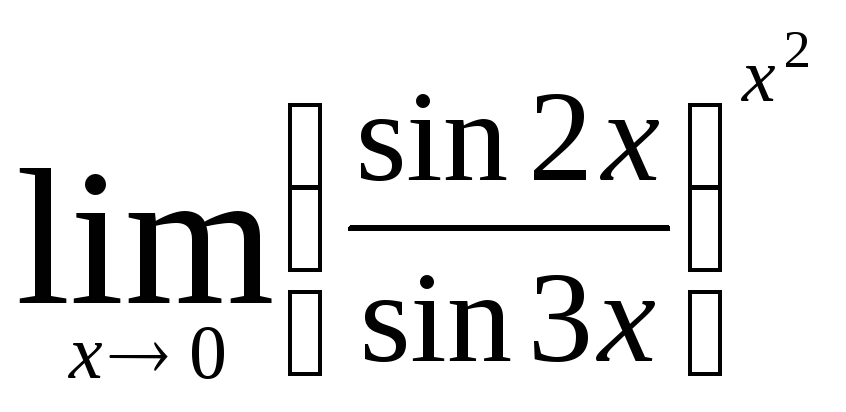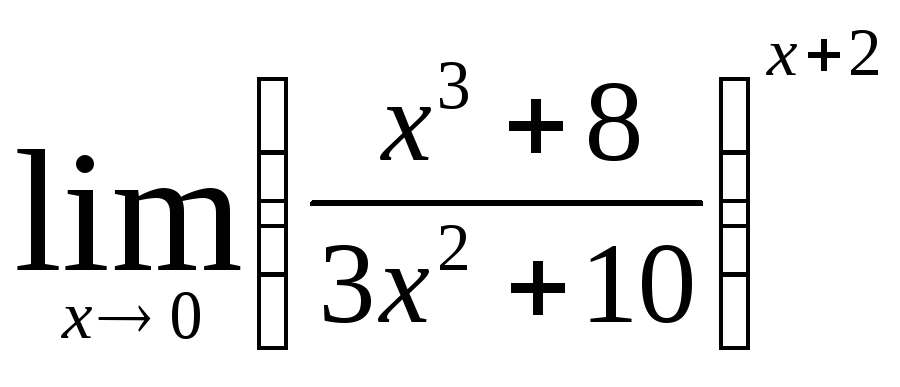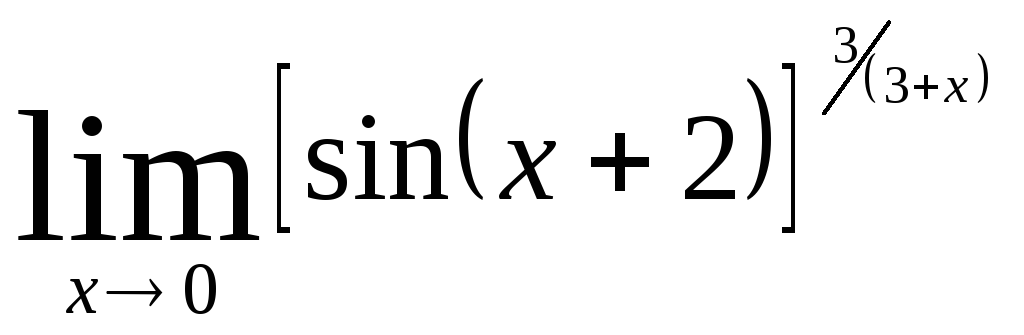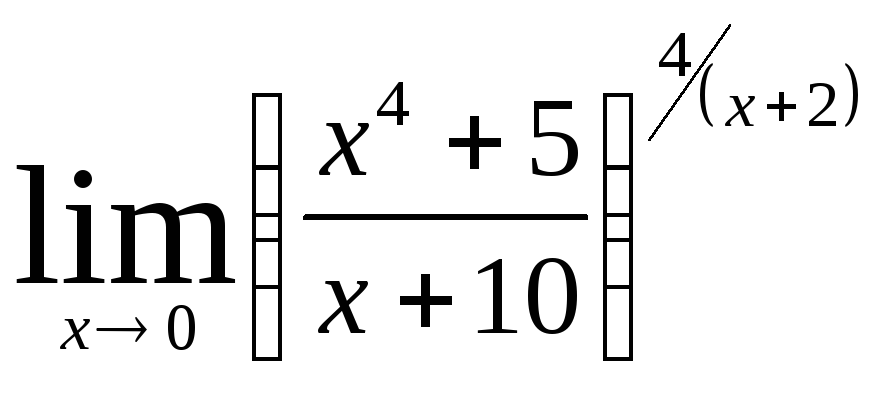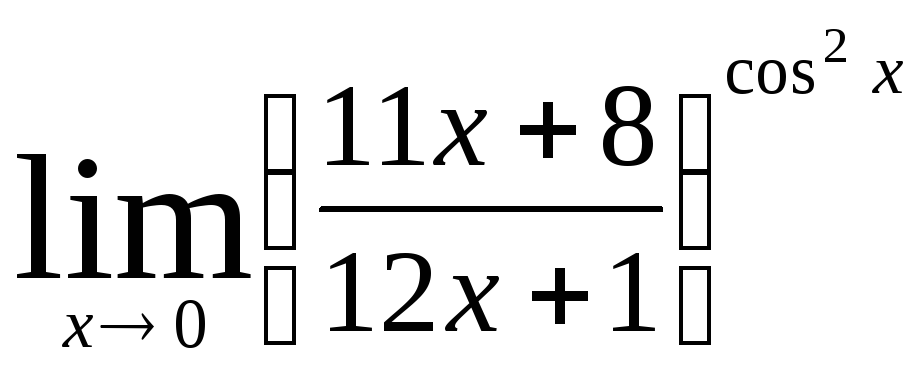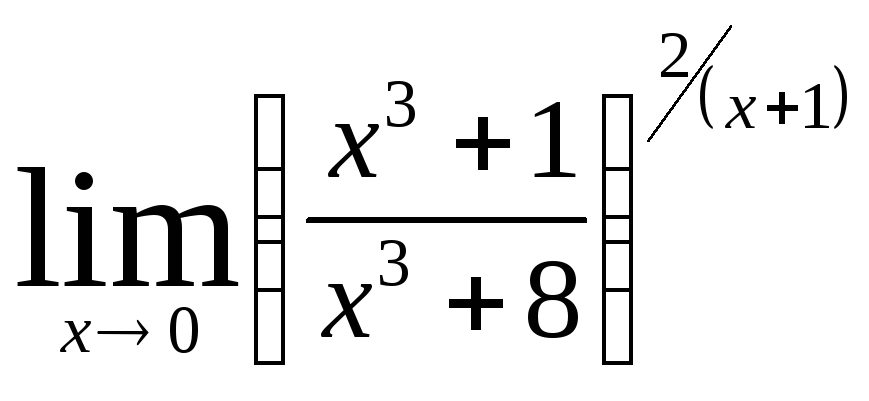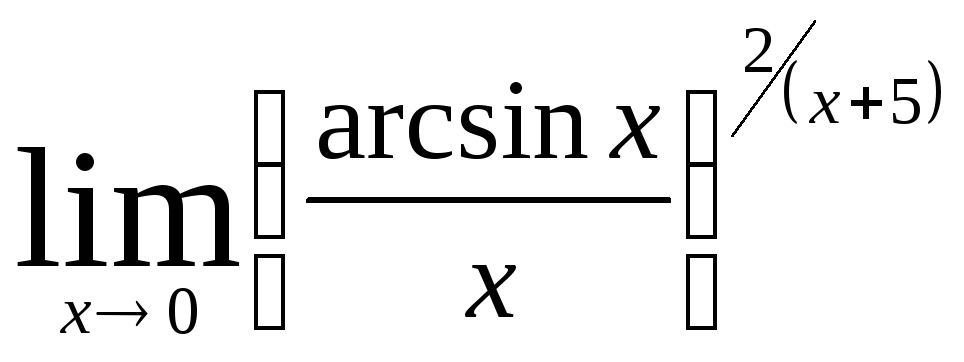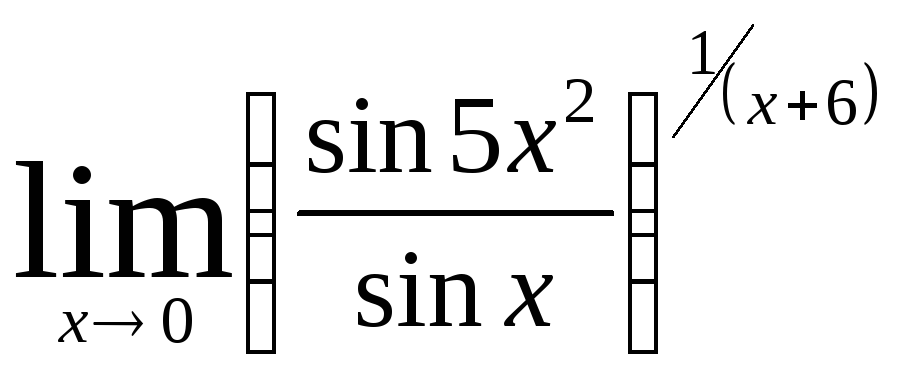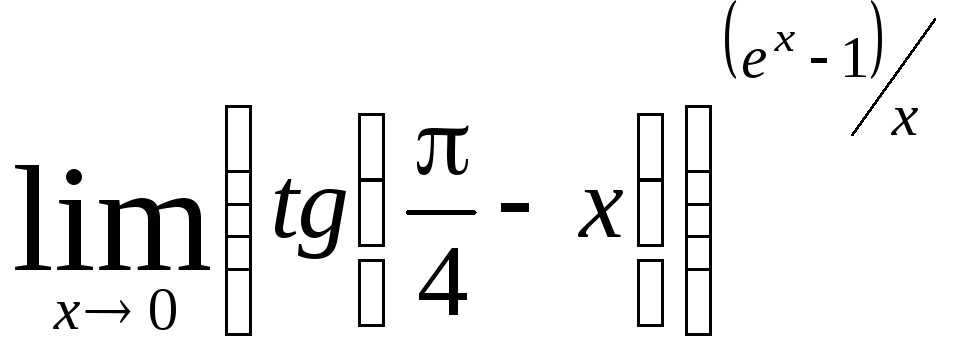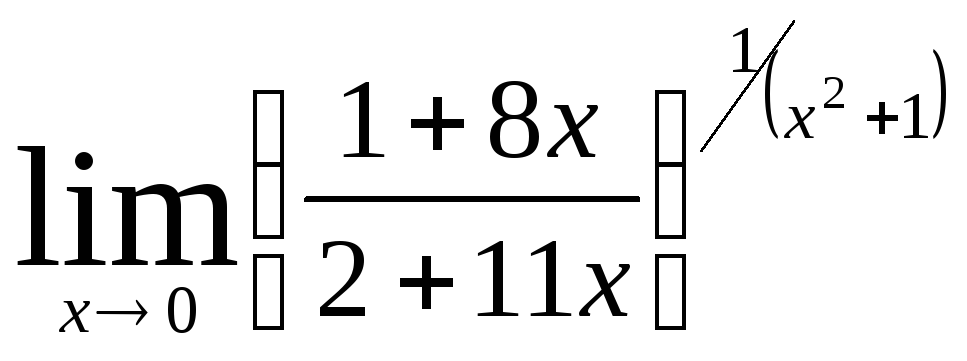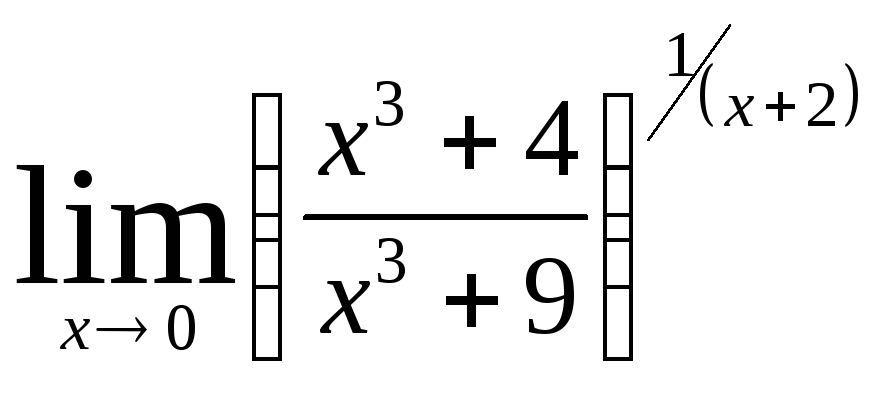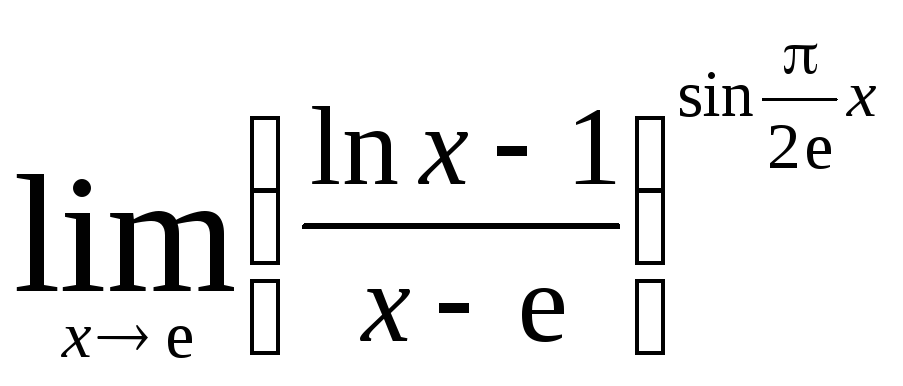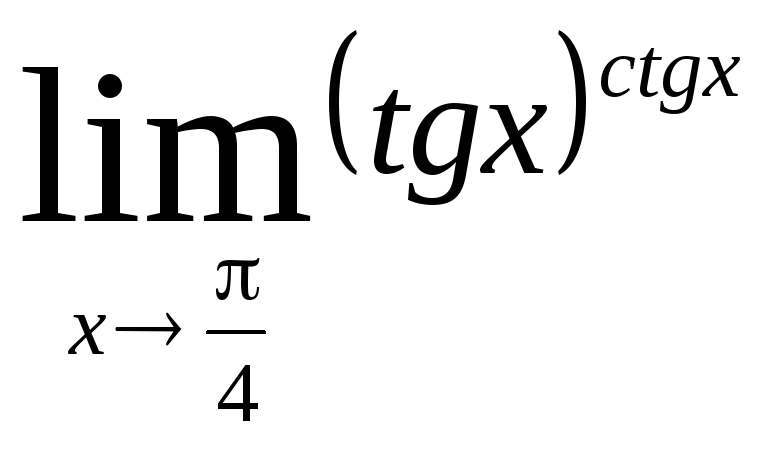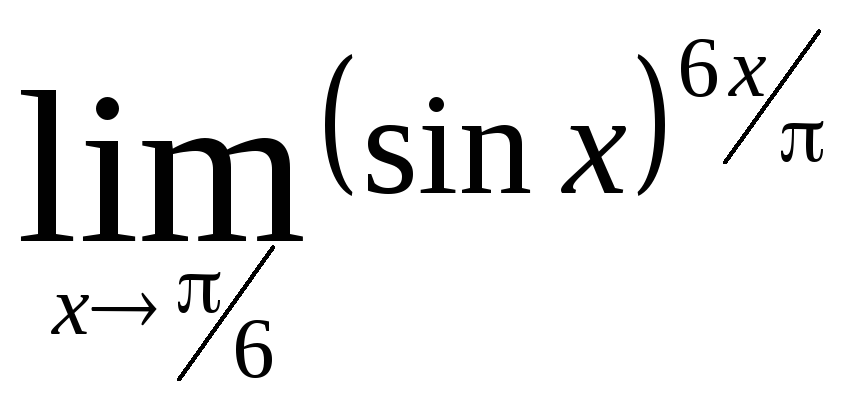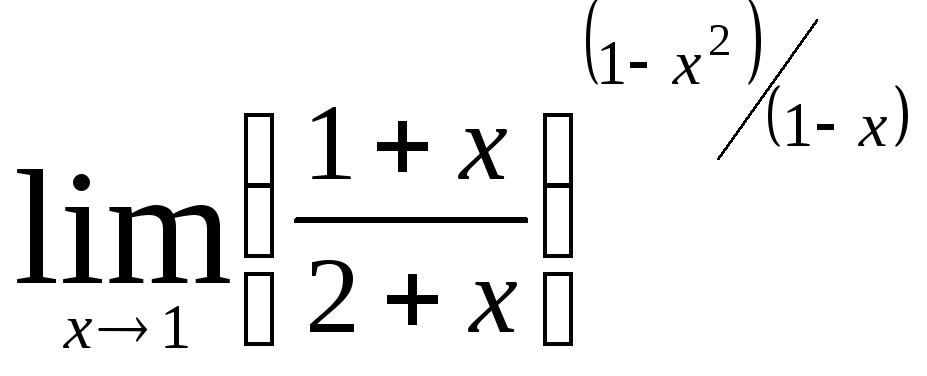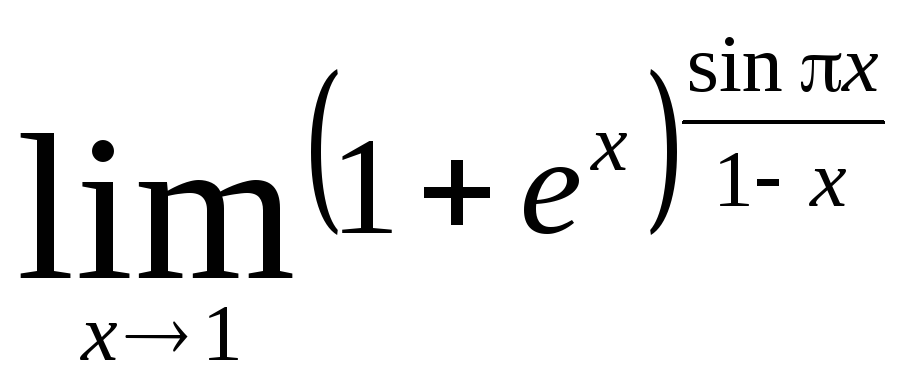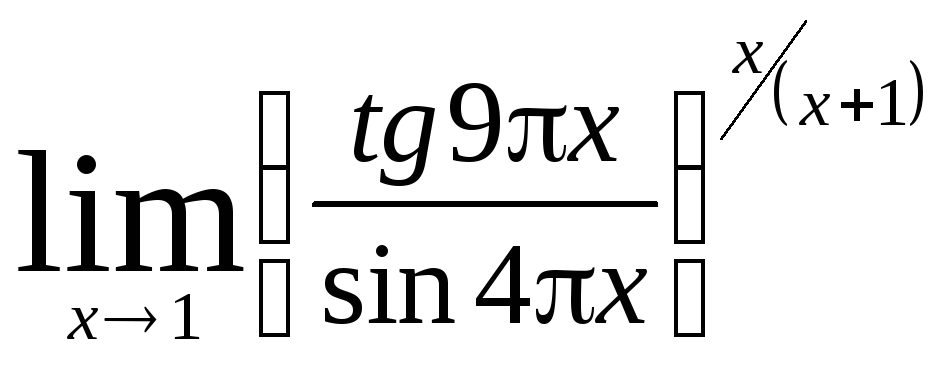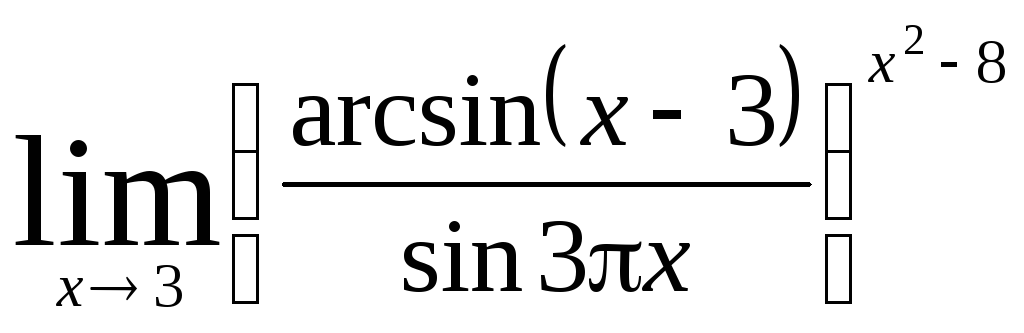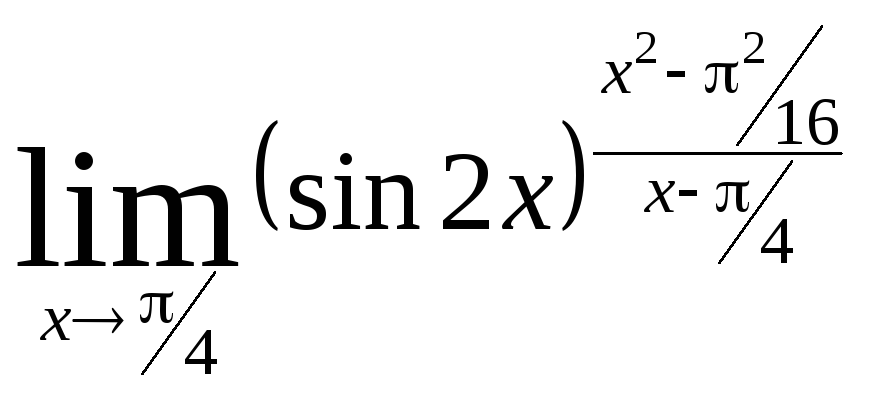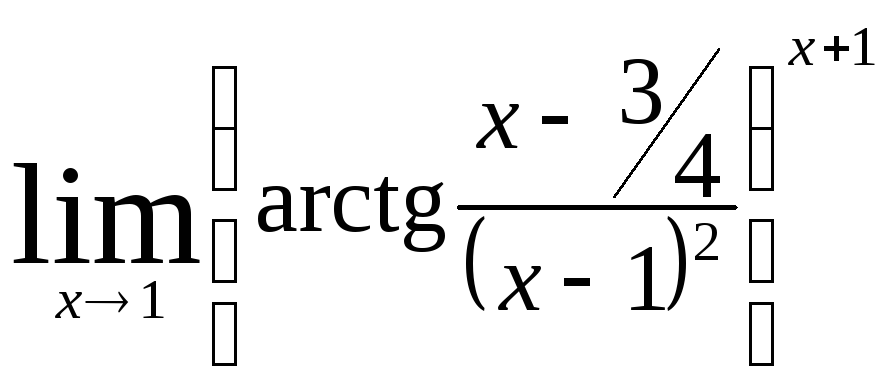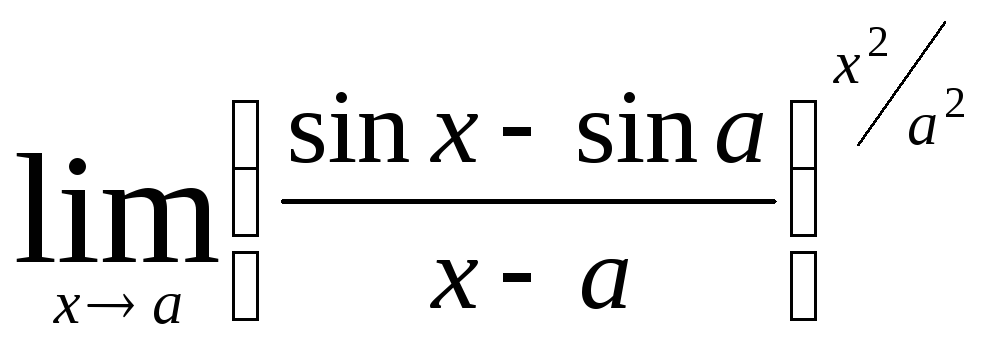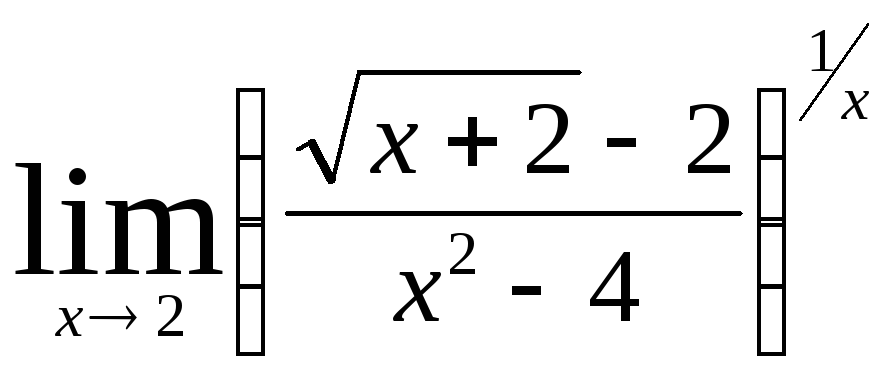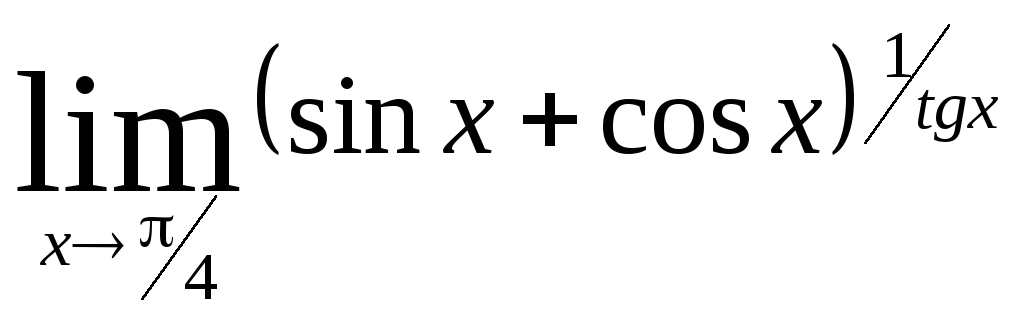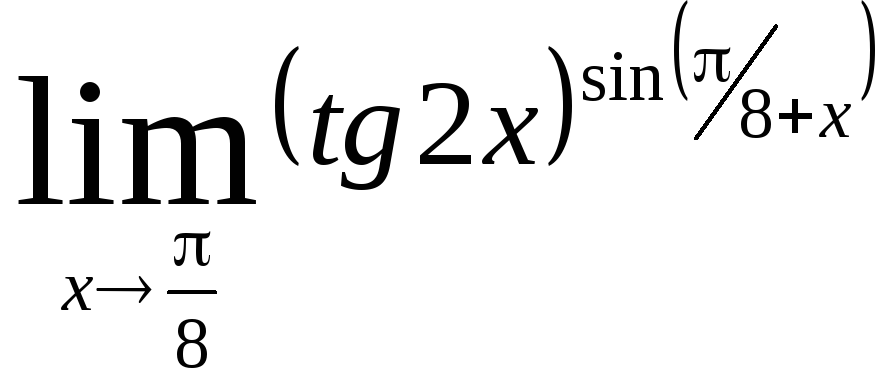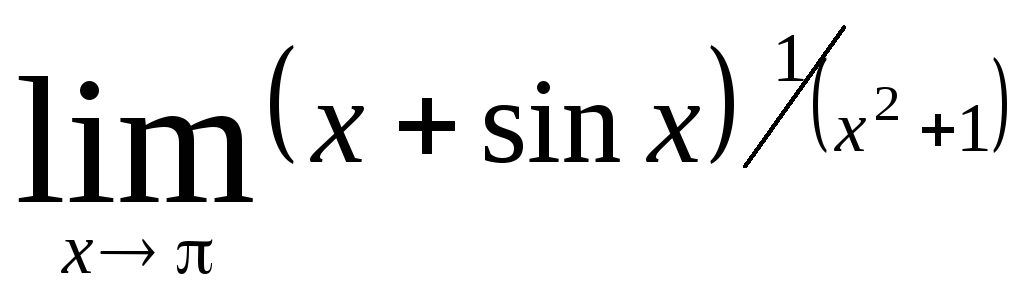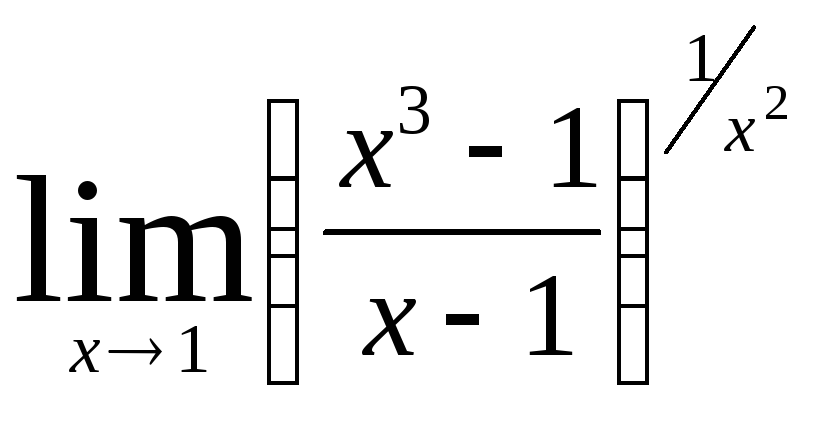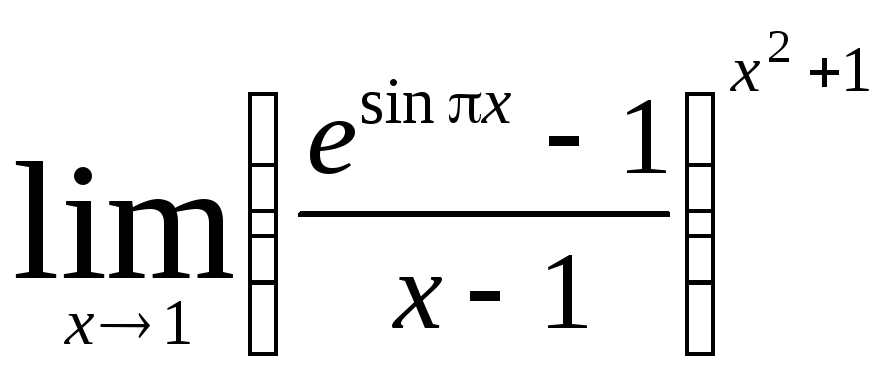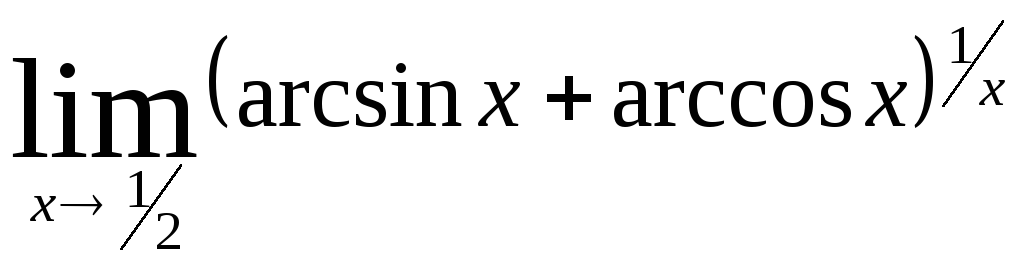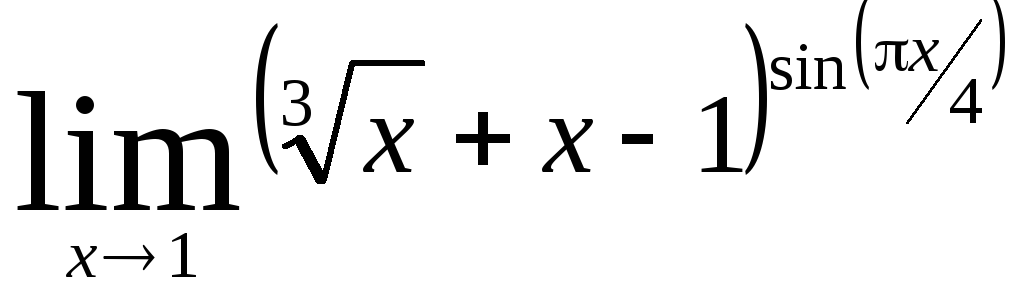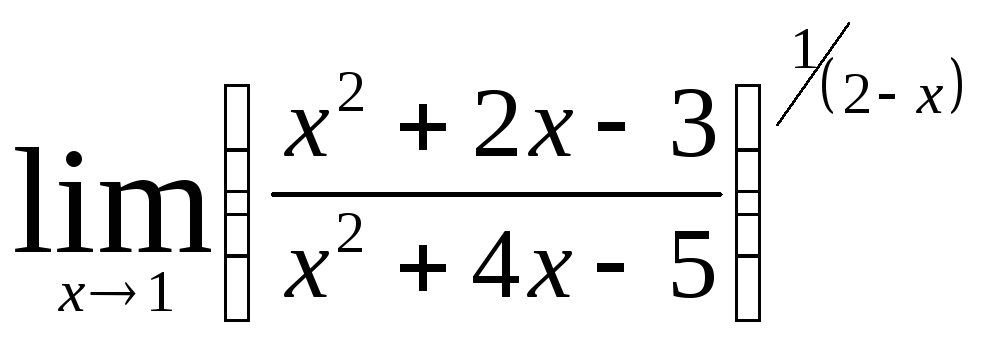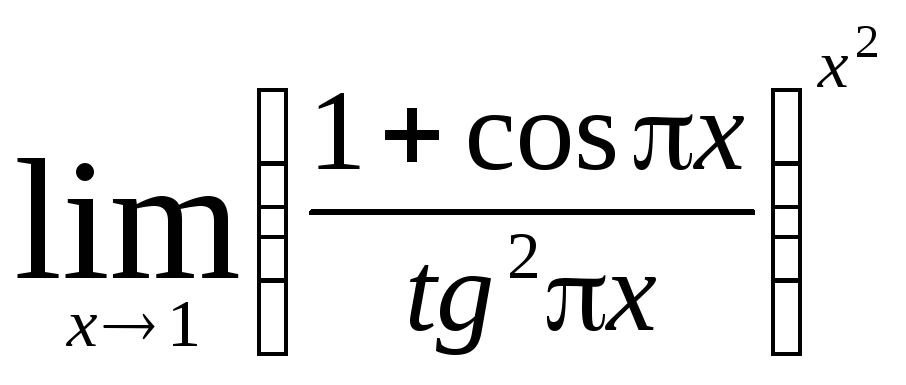Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Читинский институт Байкальского государственного университета экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика / Методические указания по теме Пределы.doc

Скачиваний:

Добавлен:

08.03.2015

Размер:

2.32 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

Министерство образования Российской Федерации

Байкальский государственный университет экономики и права

Читинский институт

Кафедра математики

Методические указания к

расчетно-графической работе

по теме

«Пределы»

для студентов 1-го курса

Чита 2010г.

Введение

Методические указания предназначены для студентов 1 курса финансово-информационного и экономического факультетов. Расчетно-графическая работа по теме «Пределы» содержит 31 однотипный вариант, каждый из которых состоит из 13 задач.

Первая задача предназначена для более глубокого понимания сути предела последовательности.

Вторая, третья и четвертая задача акцентирует внимание на раскрытии неопределенностей типа , , встречающиеся при нахождении предела последовательности.

Пятая задача демонстрирует использование второго замечательного предела при вычислении предела последовательности.

Шестая задача посвящена определению предела функции в точке.

Седьмая и восьмая задачи содержат пределы с неопределенностью , которая раскрывается с помощью формул сокращенного умножения и деления многочлена на многочлен.

Девятая, десятая и одиннадцатая задача содержат примеры с неопределенностью , для раскрытия которой требуется знание замечательных пределов и их следствий, а также знание свойств тригонометрических, логарифмических и показательных функций.

Двенадцатая и тринадцатая задача состоит из достаточно простых примеров с легко раскрываемой неопределенностью. Основной акцент здесь делается на корректном применении свойств пределов функции.

Для каждой задачи подробно рассмотрен пример решения, содержащий как необходимый теоретический материал, так и комментарии, акцентирующие внимание на основных элементах решения, где чаще всего студенты делают ошибки.

Демонстрационный вариант

Задача №1. Доказать, что (указать ).

Определение. Число называется пределом последовательности , если для всякого сколь угодно малого положительного числа найдется такое положительное число , что при выполняется неравенство .

Итак, для того, чтобы доказать, что число является пределом последовательности , необходимо для любого положительного сколь угодно малого числа указать способ (в виде формулы, правила, алгоритма) определения числа такого, что из . Например, рассмотрим последовательность или, другими словами, последовательность -ый член, которой задается формулой и докажем, что ее предел равен нулю . Для этого надо доказать, что . Это эквивалентно тому, что при . Так как – это порядковый номер соответствующего члена последовательности, то , следовательно, . Отсюда, выражение эквивалентно выражению , или выражению .

Из последнего выражения очевидно, что требуемое число существует, для любого положительного . Например, его можно определить по формуле . Действительно, если , то подставляя вместо выражение , получаем , т.е. при , что эквивалентно тому, что при . Согласно определению последовательности это означает, что число ноль является пределом последовательности .

Замечание. Число можно задать с помощью другой формулы. Например, . Имеем , т.е. . Не принципиально какую формулу Вы выберете, главное, что существует хотя бы одна такая формула.

Итак, залогом успеха приведенного доказательства является то, что нам удалось с помощью эквивалентных преобразований привести первоначальные неравенства , к сопоставимому виду , . Так как левые части неравенств совпадают, то должны совпадать и правые части. Отсюда, легко получить формулу для . Такая же идея лежит в основе любого доказательства задания №1. Кратко рассмотрим еще несколько примеров.

Пусть , . Докажем, что , т.е. найдем такое , что при . Имеем

Так как нас интересует предел последовательности при , т.е. при достаточно больших значениях , то это означает, что первые члены последовательности можно не рассматривать. В данном примере можно считать, что , тогда , следовательно, . Таким образом,

Итак, если , то , т.е. , что и требовалось доказать. Напоминаем, что вся эта логика справедлива для , т.е. когда первые три члена последовательности игнорируются, поэтому если , то полагаем .

Следующий пример. Пусть , . Докажем, что , т.е. найдем такое , что при . Имеем

Так как – это порядковый номер соответствующего члена последовательности, то , следовательно, , , . Таким образом,

Для больших значений выражение для любых . Если достаточно мало, что , то

Итак, если для больших значений и для достаточно малых значений , то , т.е. , что и требовалось доказать.

Задача 2. Вычислить пределы числовых последовательностей.

Данные примеры содержат неопределенность . Для раскрытия данного вида неопределенности в этих примерах достаточно знать формулы сокращенного умножения и некоторые свойства пределов. Напоминаем:

– формулы сокращенного умножения

– свойства пределов

, ,

, , ,

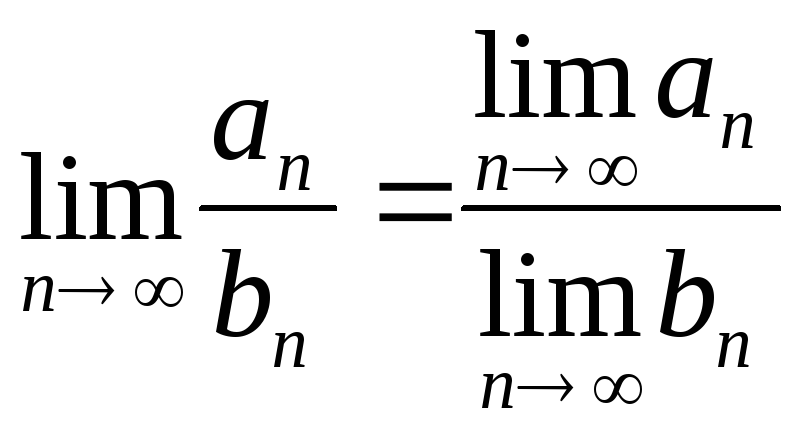а также, что или (мы это частично доказали при рассмотрении задачи №1).

Полезно помнить, что если при вычислении пределов вам встретились случаи , , то это неопределенности, которые необходимо раскрыть. Ответ в таком виде записывать нельзя. Однако если вам встретились случаи , , , , то они не являются неопределенностями и для них можно сразу записать соответствующий ответ. Покажем это, используя первый пример задачи 1.

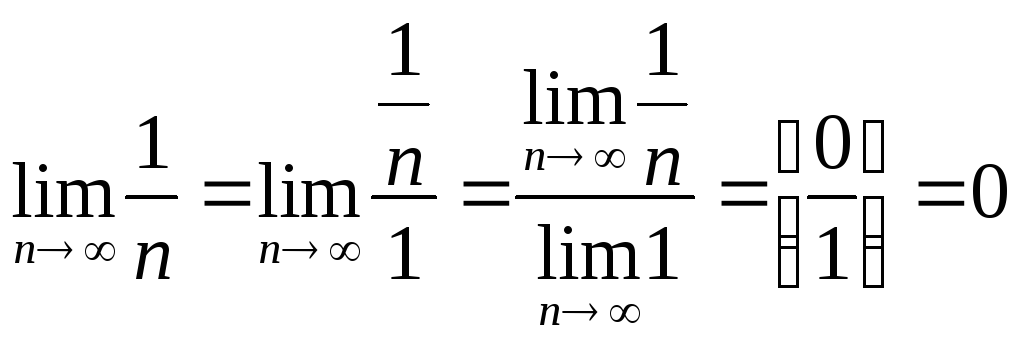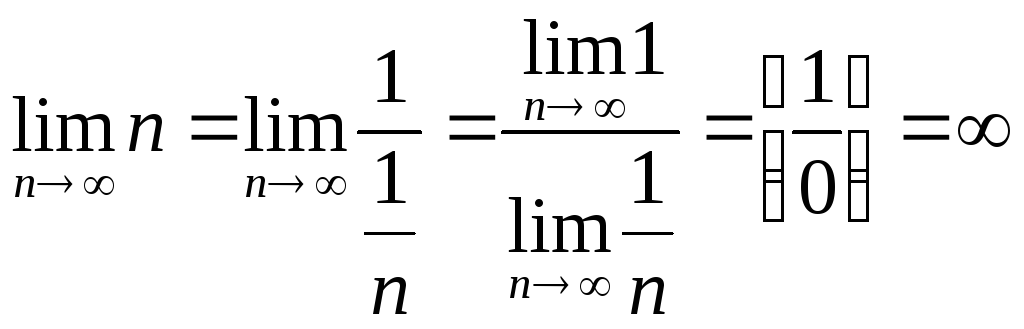Мы доказали, что . Отсюда, . Кроме того, очевидно, что при , т.е. . Отсюда, , а также . Используя свойства пределов можно показать, что всегда имеют место следующие результаты: , , , .

В записанных выражениях квадратные скобки используются, для того, чтобы подчеркнуть, что в рассматриваемых дробях подразумевается не число, например, равное нулю (иначе выражение не имело бы смысла, ведь на ноль делить нельзя), а величина очень близкая к нулю, бесконечно приближающаяся к нулю, величина, предел которой равен нулю, т.е. бесконечно малая величина. Аналогично, в выражении, например, под подразумевается не какое-либо число, а бесконечно большая величина, которая всегда больше любого сколь угодно большого числа, т.е. это нечто, что находится за пределами нашего сознания. Мы не можем до конца понять и представить себе, что такое «бесконечность», но мы можем догадаться о некоторых ее свойствах, например, что .

Пример.

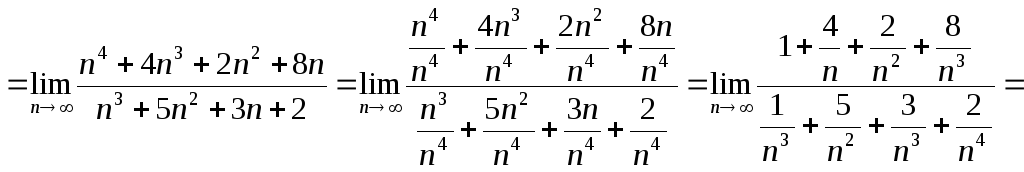
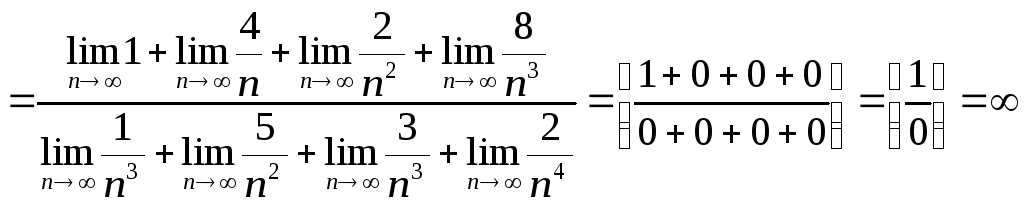
Данный пример можно было решить и другими способами. Если вы такие знаете, то, пожалуйста, решайте! Главное, чтобы пример был решен правильно, и вы понимали, логику вашего решения.

Для сравнения приведем способ решения данного примера, который очень пригодится нам при решении задачи 3.

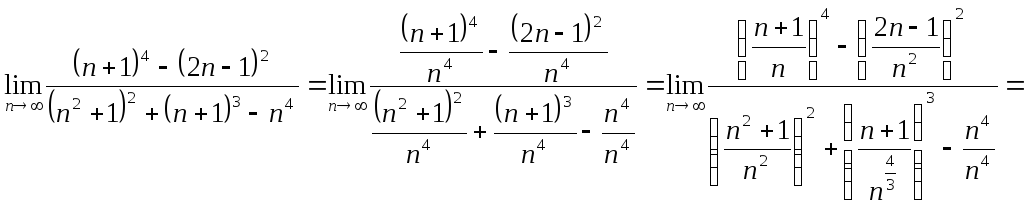
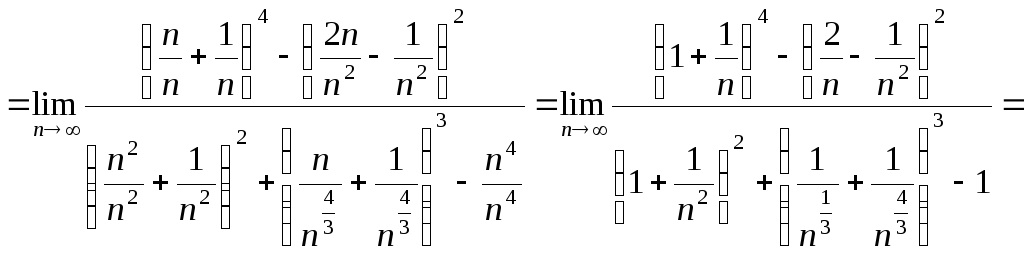
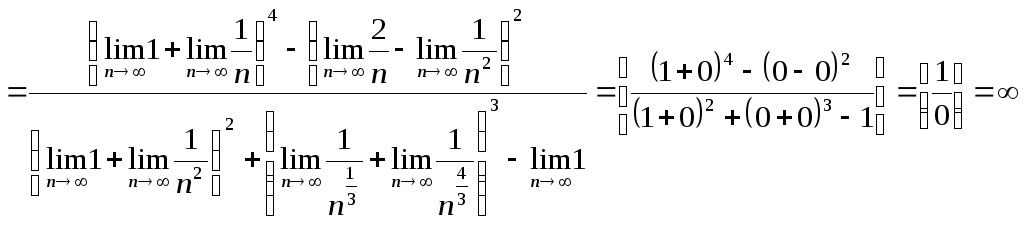
Данный способ решения не требует знания формул сокращенного умножения, но, к сожалению, им не всегда можно воспользоваться. Покажем это на следующем примере.

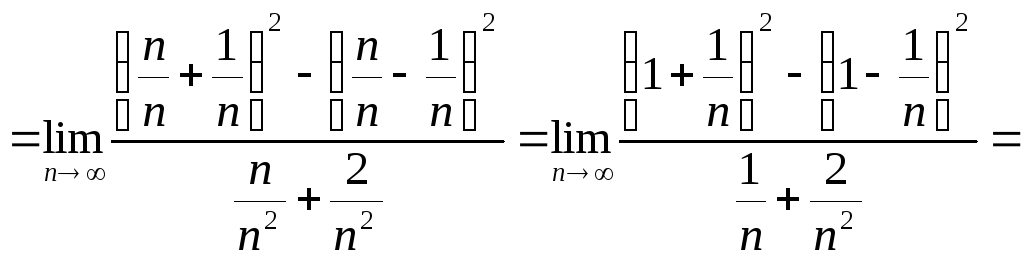
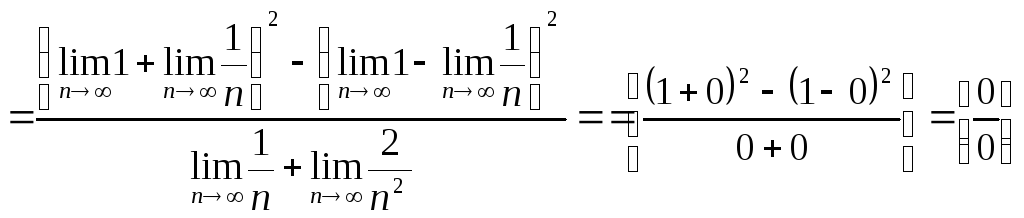
Мы получили неопределенность, поэтому надо применить первый способ решения.

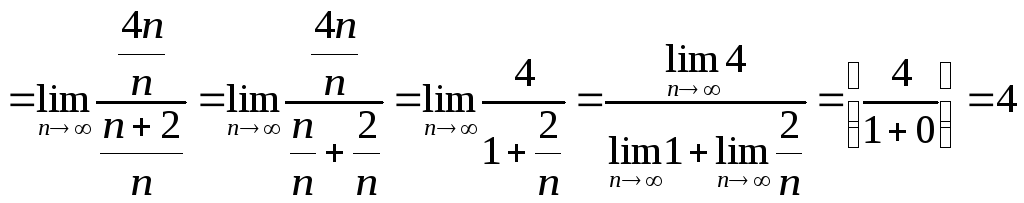Итак, при решении задачи №2 рекомендуется первый способ. Не потому, что он самый лучший, а потому, что он позволит найти решение в любом варианте задачи №2.

Задача 3. Вычислить пределы числовых последовательностей.

Задача №3 аналогична задаче №2 с той лишь разницей, что здесь присутствуют выражения с корнями, т.е. иррациональные выражения. Поскольку наличие корней затрудняет использование формул сокращенного умножения, то при решении задачи №3 рекомендуется использовать второй способ решения, рассмотренный в задаче №2.

Как мы видели в задаче №2, второй способ не всегда позволяет получить решение. Такая же ситуация в принципе возможна и в примерах с иррациональными выражениями, но поскольку работа с корнями, как правило, вызывает у студентов затруднения, то эти случаи были собраны отдельно в задаче №4. Таким образом, в задаче №3 смело используйте второй способ решения, а в задаче №4 опять придется прибегнуть к формулам сокращенного умножения.

Напоминаем, что идея второго метода заключается в том, чтобы сразу разделить числитель и знаменатель дроби на в наибольшей степени и в результате дальнейших преобразований раскрыть неопределенность . Трудности при решении данной задачи возникают при определении наибольшей степени , внесении множителя под знак корня, представлении одной дроби в виде суммы или произведения нескольких дробей и сокращении на в любой произвольной степени .

Разберем эти элементы решения по отдельности.

Определение наибольшей степени .

Во-первых, при определении наибольшей степени необходимо принимать во внимание степень корня. Например, в выражении наибольшей степенью является не 4, а 3. Это становится очевидно, если вспомнить, что , т.е. . Полезно также помнить, что любой корень можно представить в виде соответствующей степени. Например, .

Во-вторых, при определении наибольшей степени необходимо обращать внимание на произведения, так как показатели степени множителей складываются. Например, в выражении наибольшая степень равна , поскольку .

В-третьих, при оценке наибольшей степени главное сконцентрироваться на наибольших степенях в каждом корне, скобке и т.п. Остальные степени, а также различные коэффициенты можно игнорировать. Например,

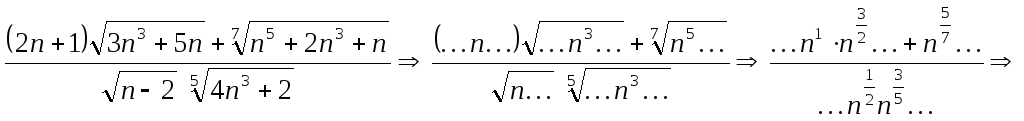
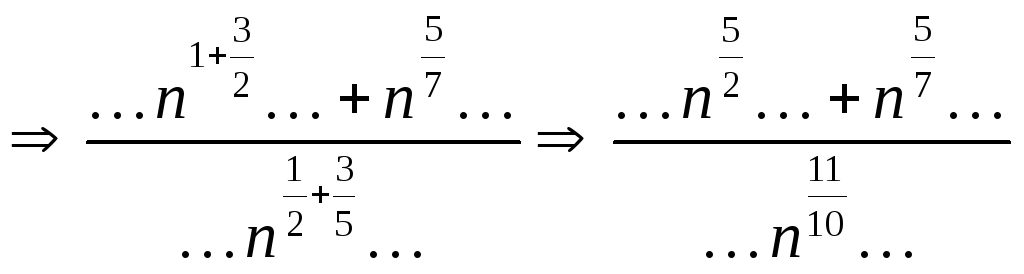
Таким образом, наибольшая степень равна .

Внесение множителя под знак корня.

При внесении под знак корня -ой степени необходимо возвести в степень , т.е. . Можно рассуждать по-другому, используя показатели степени: . Это же правило используется при внесении под знак корня множителя в любой произвольной степени : . Например, , , .

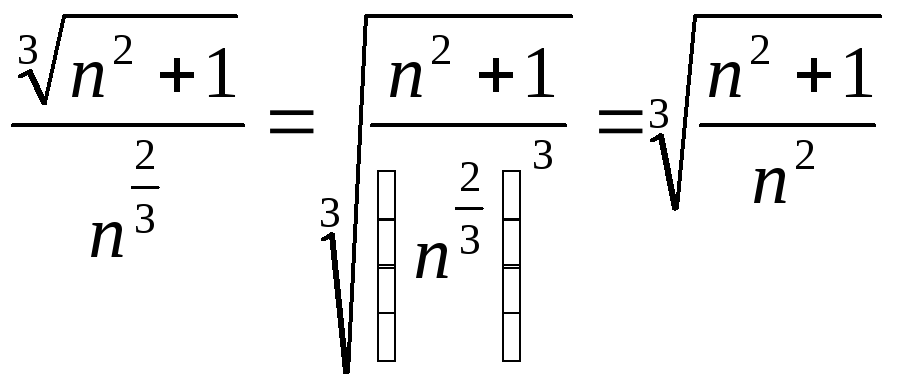Представление одной дроби в виде суммы или произведения нескольких дробей.

Если некоторая сумма делится на , то на делится каждое слагаемое. Это справедливо и для какой-либо разности. Например,

Этот случай приведен здесь не потому, что в нем часто делают ошибки, а потому, что его путают со случаем произведения. Если произведение множителей делится на , то в данном случае каждый множитель делится не на ! В данном случае также представляется в виде произведения множителей, после чего каждый множитель числителя делится на соответствующий множитель . На какие множители разложить решать вам, но обычно стараются, чтобы степень множителя была равна наибольшей степени соответствующего множителя числителя. Например,

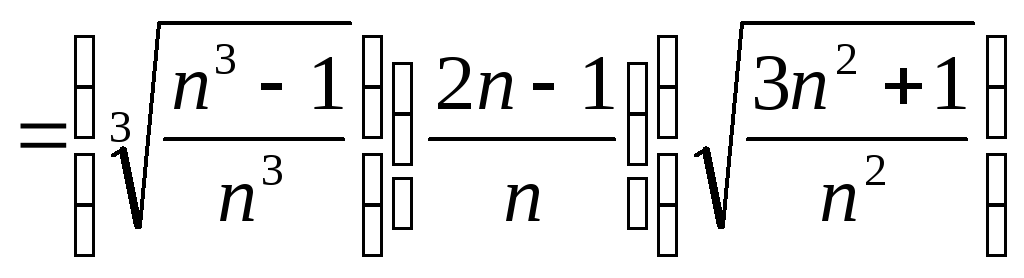
Примеры, демонстрирующие случаи, когда не удается добиться полного соответствия между множителями числителя и знаменателя:

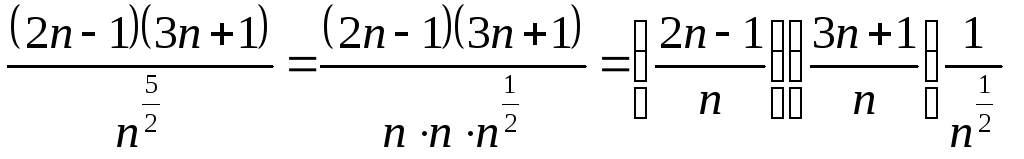
Сокращение на в любой произвольной степени .

После деления на , внесения его под корень, представления дробей в виде суммы или произведения нескольких дробей, как правило, получаются дроби вида . Следовательно, возникает необходимость сокращения числителя и знаменателя на . Правило здесь простое. Надо найти разность . Если , то . Если , то . Например,

, , ,

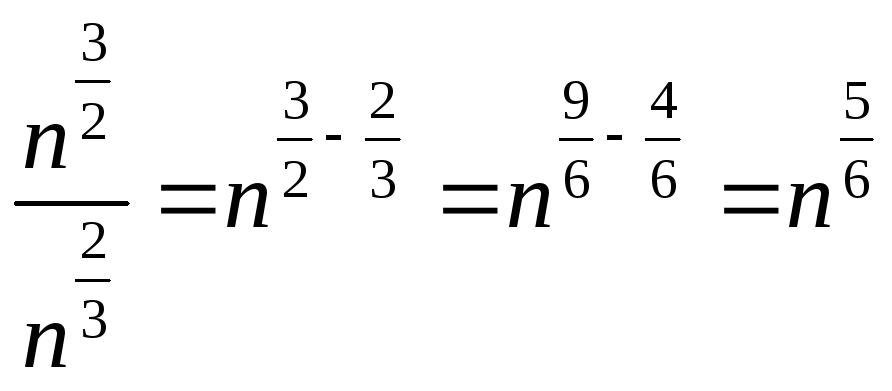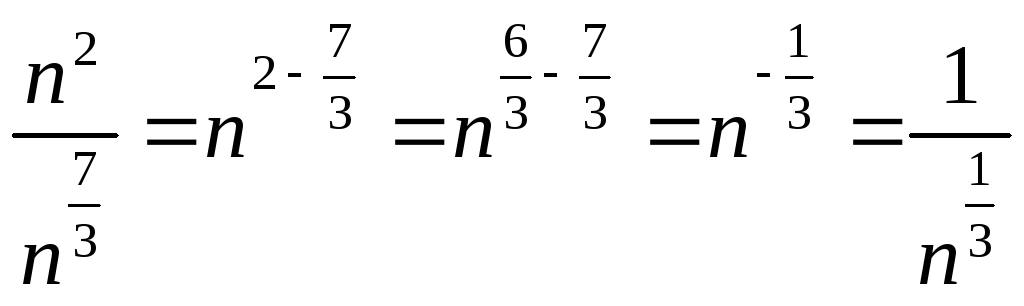
Итак, рассмотрим пример решения задачи №3:

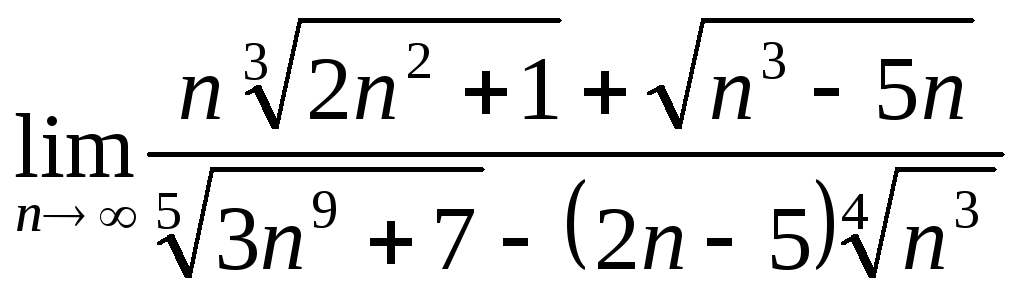
Сначала оценим наибольшую степень в заданной дроби:

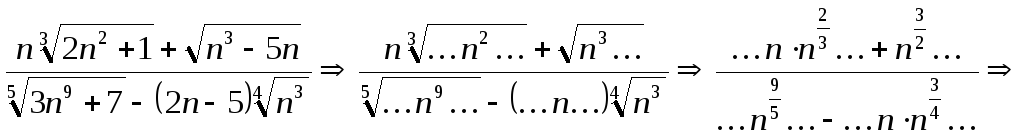
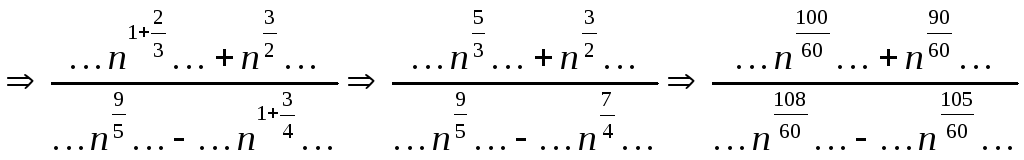
Таким образом, наибольшая степень равна . Имеем

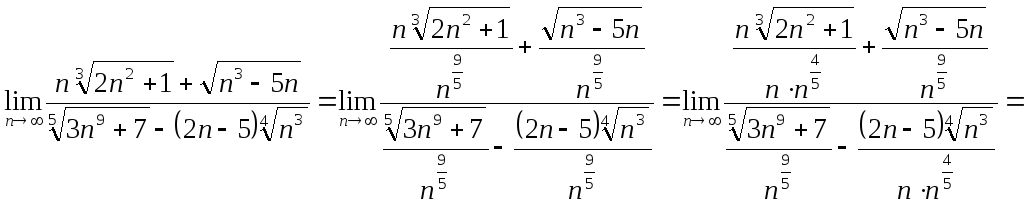
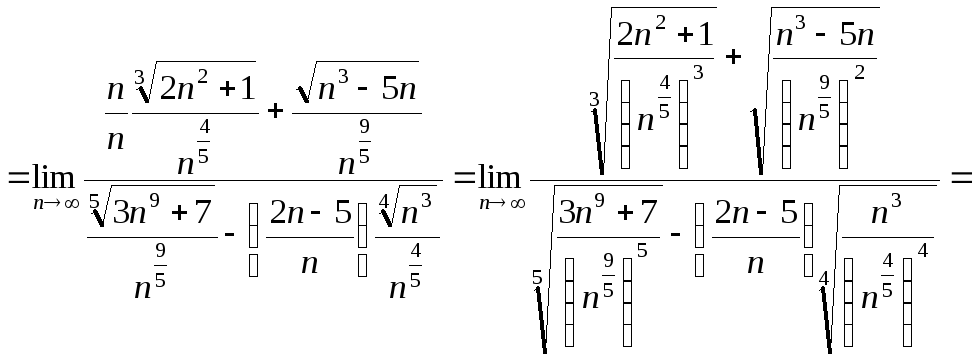
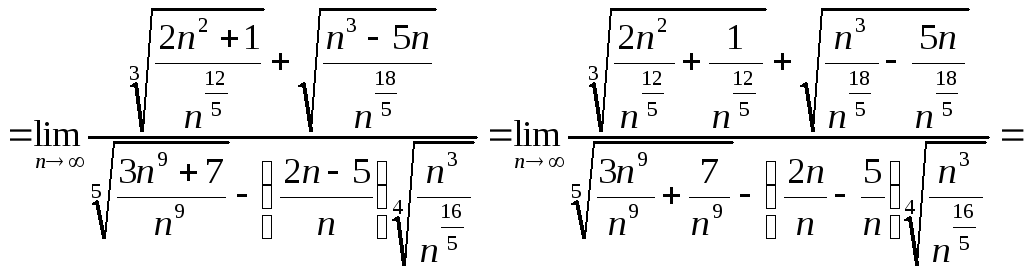
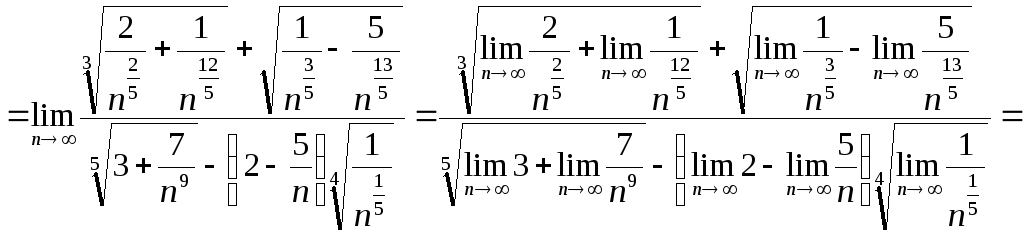
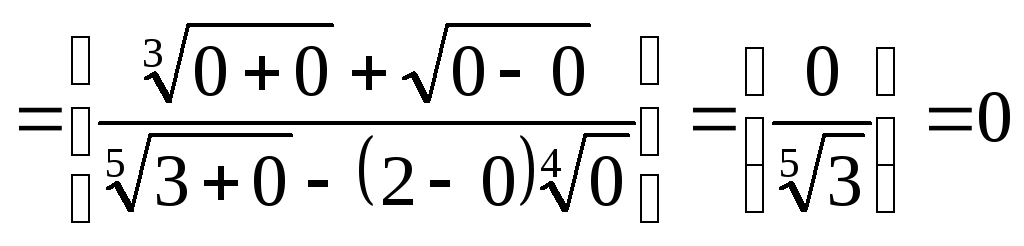
Задача 4. Вычислить пределы числовых последовательностей.

В задаче №4 во всех вариантах имеет место неопределенность вида , раскрыть которую удается только путем преобразования разности с иррациональными выражениями в разность без иррациональности, где, в свою очередь, необходимо привести подобные. Раскрыв таким образом неопределенность , получаем неопределенность , которую раскрываем аналогично решению задачи №3.

Устранение иррациональности из заданной разности проводится с помощью следующих формул сокращенного умножения:

Например,

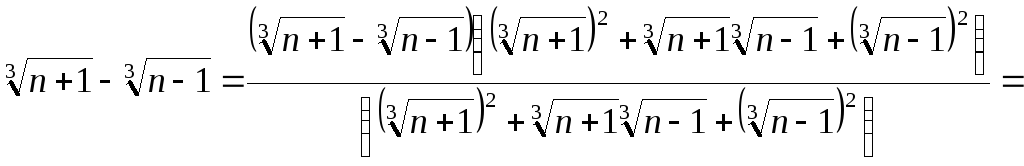
Итак, использование формул сокращенного умножения позволило в числителе избавиться от иррациональности и в результате устранить причину неопределенности , приведя подобные . Побочным результатом данного алгоритма является появление иррациональности в знаменателе, но это уже сумма иррациональностей, а не разность. Это принципиально, так как неопределенность есть, а неопределенности нет.

Замечание. В некоторых вариантах встречаются выражения, изначально содержащие не разность, а сумму слагаемых с корнем третьей степени (с квадратным корнем это невозможно). Здесь может создаться впечатление об отсутствии неопределенности, об опечатке. Это обманчивое впечатление. Причиной такой ситуации является существование корня третьей степени от отрицательного числа. Это означает, что знак минус можно вносить под знак корня, тем самым формально сделав из разности сумму. Зная причину, можно легко исправить ситуацию. Для этого надо только вынести знак минус за знак корня третьей степени, а дальше решать так, как это показано выше.

Например,

Итак, рассмотрим пример решения задачи №4:

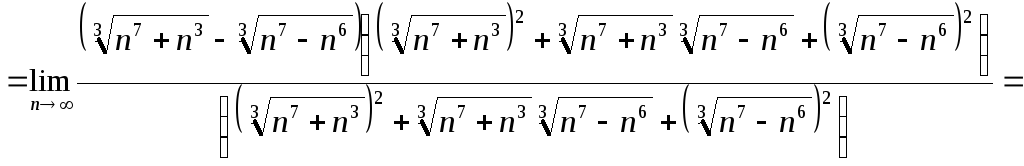
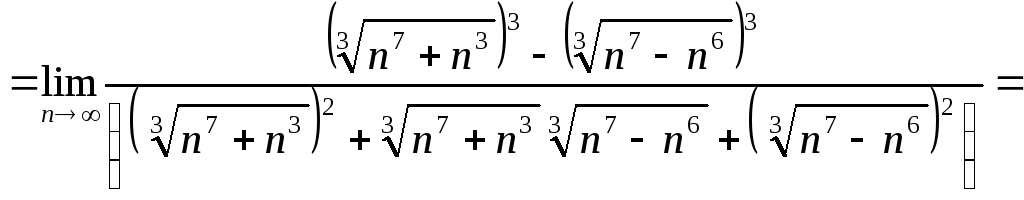
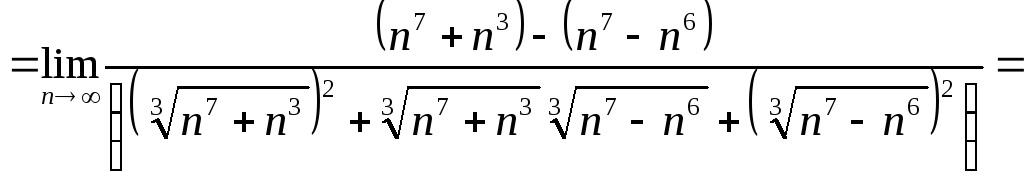
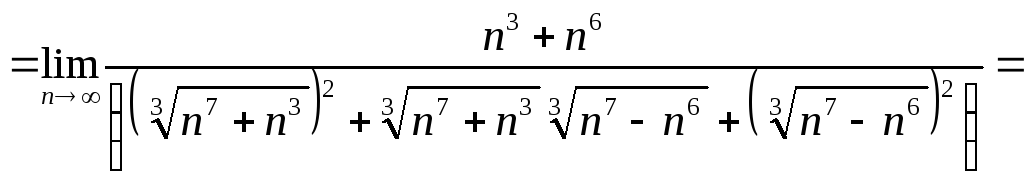
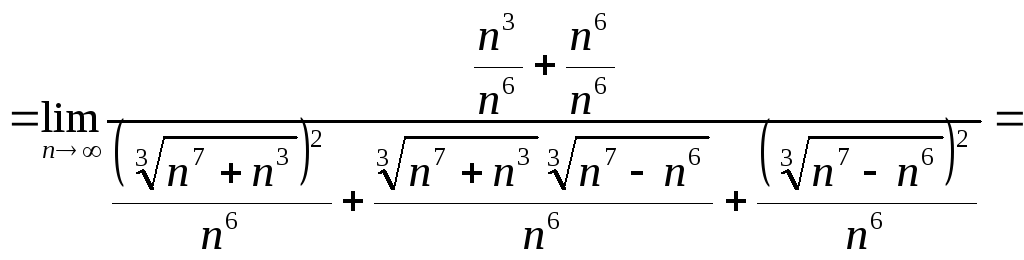
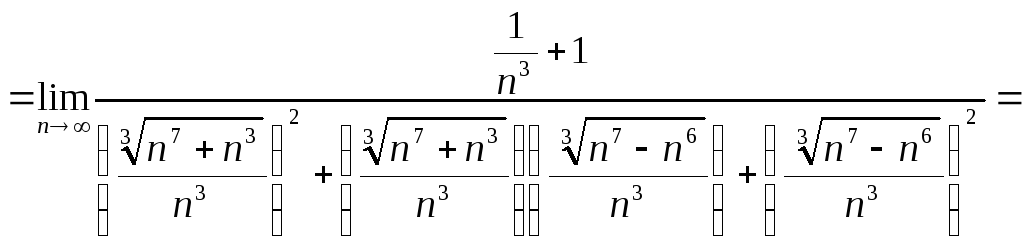
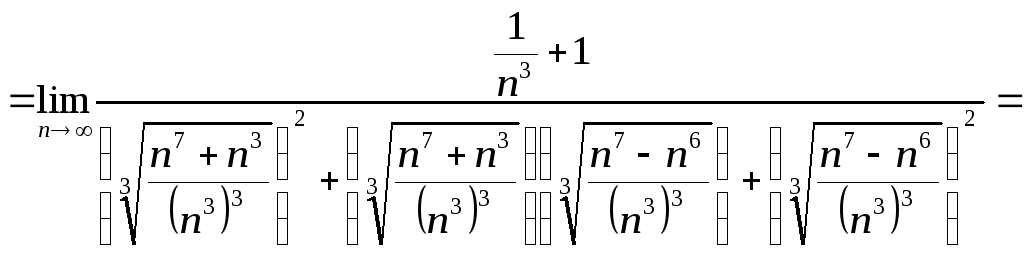
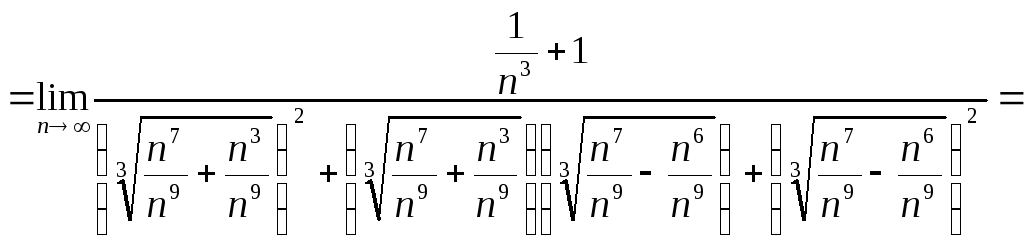
Задача 5. Вычислить пределы числовых последовательностей.

Задача №5 содержит неопределенность , поэтому она не похожа ни на одну из предыдущих задач. Раскрытие неопределенности данного вида выполняется с помощью второго замечательного предела: . Основной способ использования данного предела заключается в том, чтобы с помощью замены переменной привести заданный предел к второму замечательному пределу. Например,

Еще один пример.

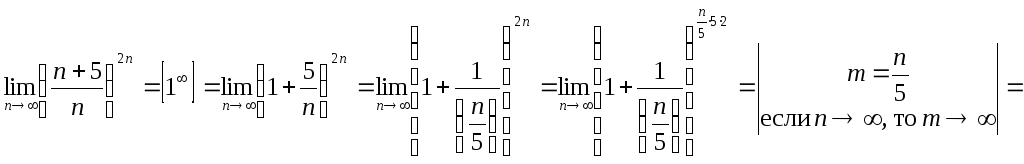
Аналогично, решается задача №5 любого варианта. Например,

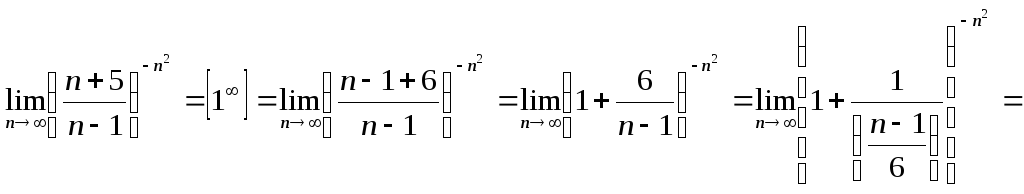
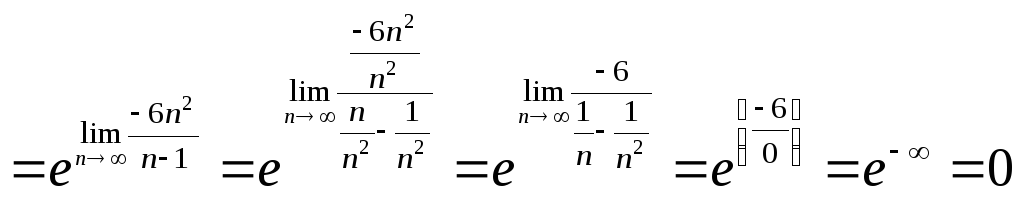
Разберем последний пример подробнее.

Первым этапом решения было выделение единицы из дроби, стоящей в круглых скобках: . Если вы не можете догадаться, как это сделать, то можете воспользоваться следующей простой идеей: нужна единица? – прибавьте ее и отнимите! Выглядит это так:

Вторым этапом решения является получение единицы в числителе полученной дроби. Здесь мы пользуемся тем, что любую дробь можно представить в виде трехэтажной дроби: .

Третьим этапом является умножение и деление показателя степени на выражение, стоящее в знаменателе дроби в круглых скобках, с тем, чтобы после замены переменной переменная была и в знаменателе и в показателе степени, т.е. чтобы получить второй замечательный предел: .

Четвертым этапом находится предел выражения, оставшегося в показателе степени. Число в полученной степени и является искомым пределом. Напоминаем, что и более того . Например, . Объясняется это просто. Очевидно, что , , . Отсюда, . Если , то . Отсюда, , .

Основным недостатком представленного способа решения является то, что среди свойств пределов нет такого свойства, согласно которому

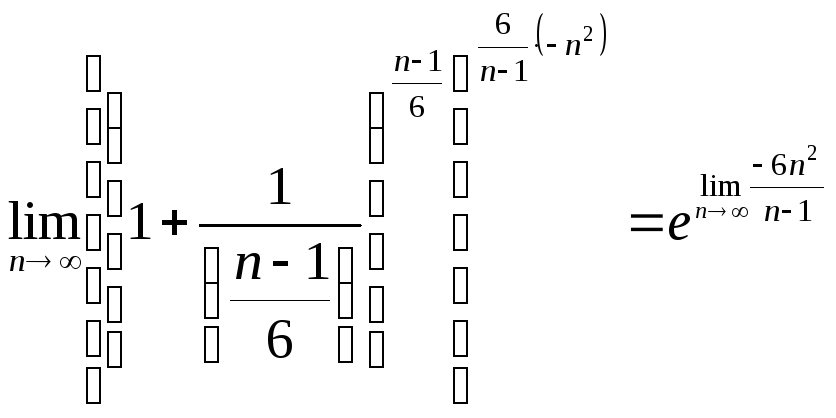
Спрашивается: на каком основании мы можем это сделать? Другими словами, это надо доказать. Вы скажете: если это до сих пор не доказано, то как мы можем это доказать? Ответим: не доказано свойство такого вида в общем случае, но это не означает, что его нельзя доказать для некоторого частного случая. В нашем случае надо показать только, что , если известно, что при . Здесь нам пригодится еще одно свойство пределов, не указанное в задаче №2: , где – некоторая непрерывная функция. Так как – непрерывные функции и , то имеем

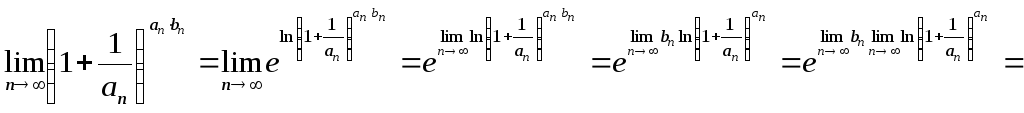
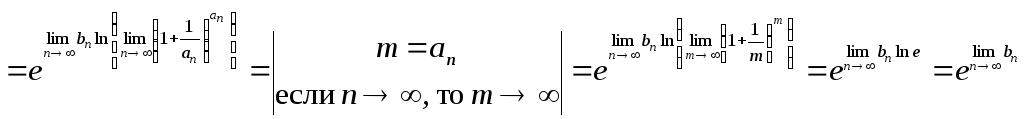
что и требовалось доказать.

Итак, теперь все корректно, т.е. задачу №5 можно и нужно решать, используя рассмотренный выше алгоритм.

Задача 6. Доказать (найти ), что .

Число называется пределом функции при , если для любого сколь угодно малого найдется такое , что при выполняется неравенство .

Итак, для того, чтобы доказать, что число является пределом функции при , необходимо для любого положительного сколь угодно малого числа указать способ (в виде формулы, правила, алгоритма) определения числа такого, что из .

Идея доказательства для предела функции аналогична идее доказательства для предела последовательности, подробно рассмотренной в задаче №1. Поэтому не будем повторяться, а перейдем сразу к примеру.

Доказать, что

Итак, для любого надо указать способ определения такого, что

Как и в задаче №1 основная идея доказательства заключается в том, чтобы привести эти неравенства к сопоставимому виду, т.е. к виду, когда левые части неравенств совпадают. Тогда должны будут совпадать и правые части, что и позволит найти требуемую зависимость . Наиболее быстрый и надежный способ добиться этой цели в любом варианте задачи №6 – разделить многочлен в числителе на многочлен в знаменателе. В нашем примере

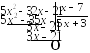
имеем

Таким образом, если для любого взять , то , а, следовательно, , т.е. , что и требовалось доказать.

Задача 7. Вычислить пределы функций.

Все варианты задачи №7 представляют собой пределы вида . Так как при многочлены в числителе и знаменателе дроби обращаются в ноль, то эти многочлены можно разложить на множители, среди которых точно есть множитель . Поскольку именно этот множитель, присутствующий и в числителе, и в знаменателе является причиной неопределенности , то, разделив на него числитель и знаменатель, удается раскрыть неопределенность. Если после сокращения неопределенность не исчезла, то это означает, что надо еще раз разделить числитель и знаменатель на множитель и так до тех пор, пока неопределенность не исчезнет. Например,

На этих примерах хорошо видно, что идея нахождения пределов такого вида очень простая и легко реализуемая при условии, что многочлены в числителе и знаменателе разложены на множители. Собственно разложение на множители в этих примерах использовалось только для того, чтобы наглядно показать способ раскрытия неопределенности путем деления числителя и знаменателя на . Поскольку в любом варианте задачи №7 многочлены не разложены на множители, то мы и не будем получать это разложение, а лучше сразу будем делить каждый многочлен на . Например,

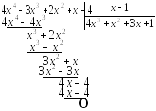
Напоследок отметим, что если выражение в числителе или знаменателе представляет собой произведение двух многочленов, то нет необходимости раскрывать скобки. Достаточно разделить на один из множителей, который обращается в ноль при . Например,

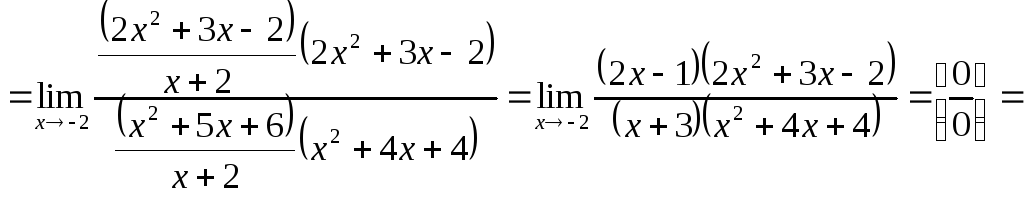
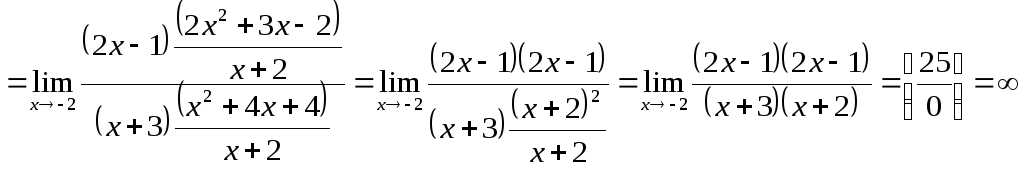
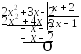
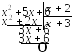
Задача 8. Вычислить пределы функций.

Задача №8 отличается от задачи №7 только наличием иррациональности, которую надо устранить с помощью формул сокращенного умножения. После того, как иррациональность устранена, дальнейшее решение аналогично решению задачи №7.

Похожая ситуация наблюдалась при решении задачи №4. В задаче №4 с помощью формул сокращенного умножения устранялась иррациональность, после чего числитель и знаменатель дроби делились на в наибольшей степени (также как в задаче №3). В задаче №8 с помощью этих формул сокращенного умножения устраняется иррациональность, после чего числитель и знаменатель дроби делятся на (также как в задаче №7). Другими словами, если вы хорошо разобрались с решением задачи №4, то вам не составит труда решить и задачу №8.

Итак, аналогично задаче №4 устранение иррациональности из разности, стоящей в числителе или знаменателе дроби, проводится с помощью следующих формул сокращенного умножения:

Если вместо разности дробь содержит сумму двух слагаемых стремящуюся к нулю при , причем хотя бы одно из них является корнем третьей степени из многочлена, то это означает, что надо вынести за знак корня знак минус. К полученной таким образом разности применяем приведенные выше формулы сокращенного умножения.

Рассмотрим конкретные примеры.

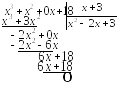
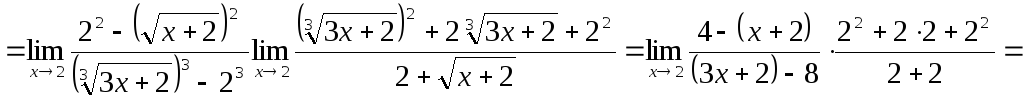
Напоследок отметим, что если в процессе преобразований появляется возможность сократить какие-либо выражения, стремящиеся к нулю при , то их надо сокращать, а не стараться во что бы то ни стало сократить на . Например,

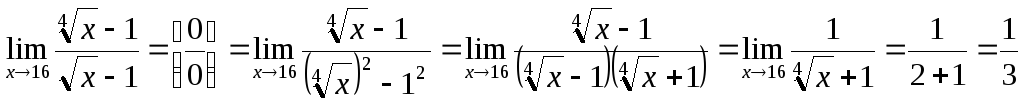
Задача 9, задача 10, задача 11. Вычислить пределы функций.

Задачи №9, №10, №11 ничем не отличаются друг от друга. Это итоговые задачи, в которых собраны почти все возможные элементы, которые можно встретить в учебных примерах на нахождение предела функции, включая и те элементы, которые уже встречались в задачах №7 и №8. Отсутствует здесь только второй замечательный предел, наверно, потому, что его более логично рассматривать с точки зрения предела последовательности (задача №5). Так как собирать все эти элементы в рамках одного варианта нецелесообразно в виду большой громоздкости получаемых пределов и их решений, то все эти элементы были случайным образом распределены по различным вариантам задач №9, №10, №11. В результате варианты одной и той же задачи получились неравноценные: где-то сложнее, где-то проще, кому как повезет.

Общей чертой всех вариантов задач №9, №10, №11 является необходимость использования табличных пределов, которые представляют собой или замечательные пределы, или следствия из них.

Первый замечательный предел 1.	Второй замечательный предел 2.
Следствия из замечательных пределов
1.1.	2.1.
1.2.	2.2.
1.3.	2.3.
1.4.	2.4.
	2.5.
	2.6.

Для того, чтобы использовать табличные пределы необходимо заданные пределы привести к табличному виду с помощью замены переменной. Например,

Как видим не имеет значения насколько сложное выражение обозначается через , главное, чтобы в результате получился один из табличных пределов. Подчеркнем, что в исходном пределе не важно к чему стремится , главное, чтобы стремился к нулю (исключение составляет второй замечательный предел). Например,

Рассмотрим еще пару примеров.

Несмотря на то, что в первом пределе первый замечательный предел получить не удалось, так как , а надо, чтобы . Во втором пределе при имеем , однако поскольку не стремится к нулю, то не стремится к нулю и первый замечательный предел также не получается. Что же делать в этих случаях? Ответ прост – просто записать ответ, ведь здесь нет никакой неопределенности.

, .

На рассмотренных простых примерах была представлена основная идея решения задач №9, №10, №11. Однако это не означает, что эти задачи простые. Во-первых, в каждом пределе эту идею надо применить не один, а несколько раз. Например,

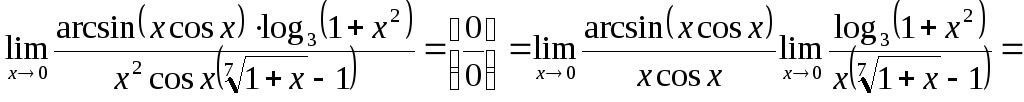
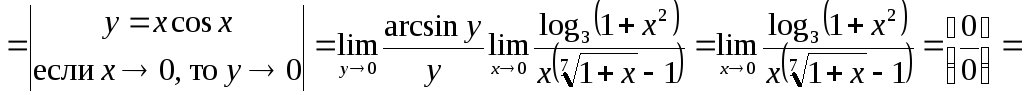
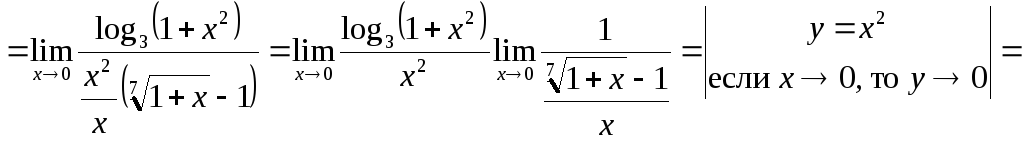
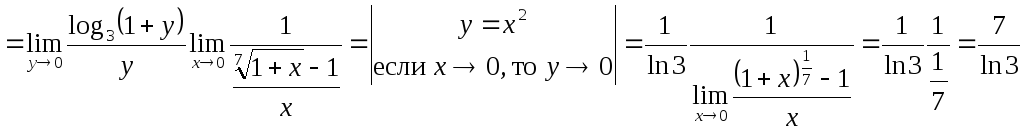
Во-вторых, для того, чтобы в результате замены переменной получился табличный предел необходимо выполнить соответствующие преобразования. Поскольку именно с выполнением преобразований студенты испытывают наибольшие трудности, разберем наиболее распространенные из них.

Умножение и деление на одно и то же выражение.

Вынесение общего множителя за скобку.

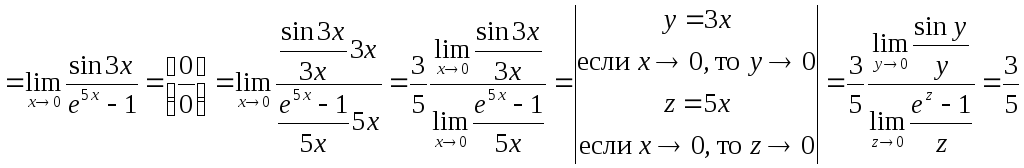
Использование формул суммы, разности тригонометрических функций и свойств логарифмов.

Напоминаем

, .

Пример.

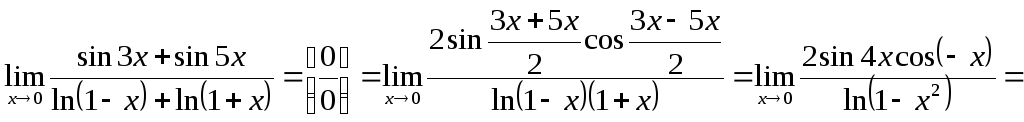
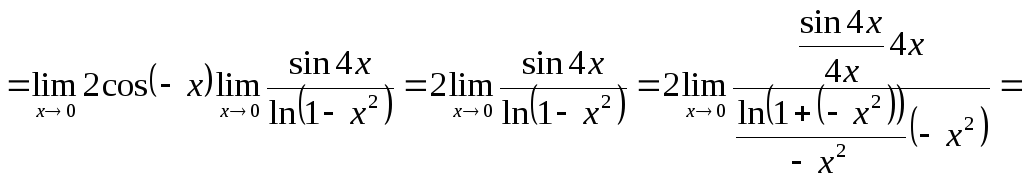
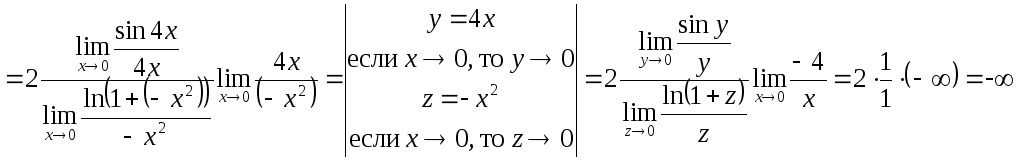
Переход от переменной, не стремящейся к нулю, к переменной, которая стремится к нулю, а также использование формул приведения.

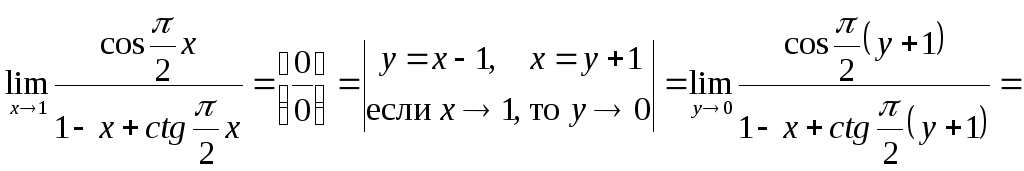
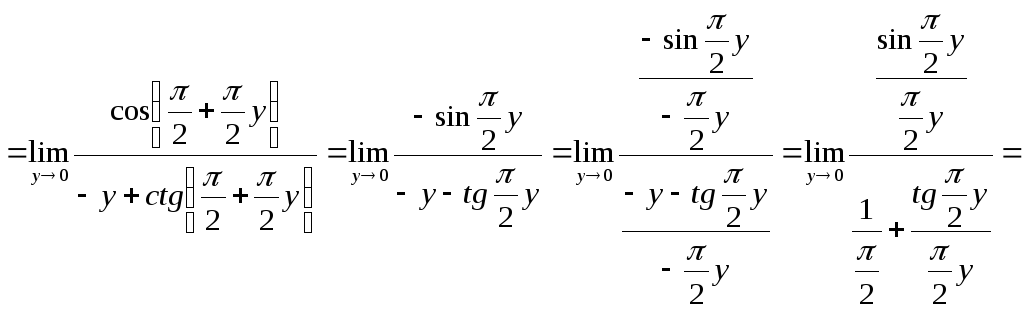
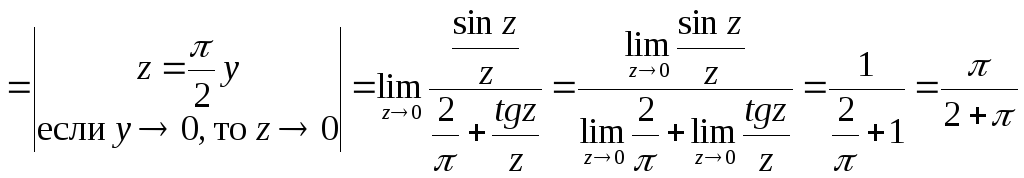
Использование формул сокращенного умножения.

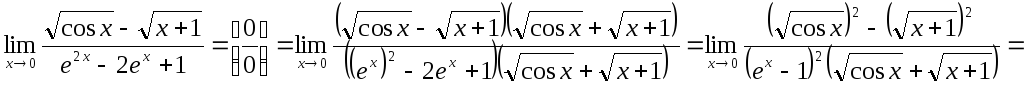
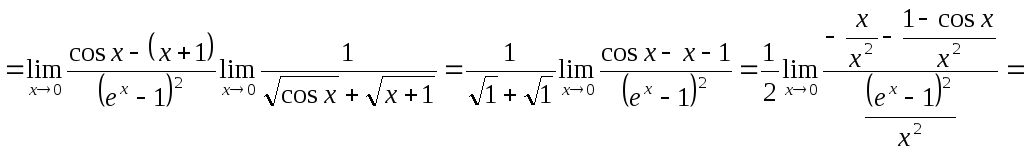
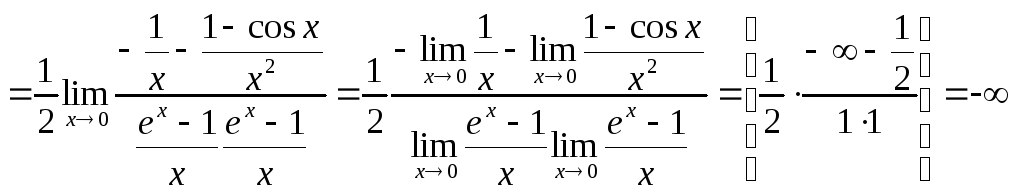
В завершении обратим ваше внимание на то, что нельзя, например, представить предел суммы в виде суммы пределов, частично упростить пределы, а затем обратно представить сумму полученных пределов как предел суммы. В некоторых задачах подобные преобразования действительно приводят к правильным ответам, но это не правильное решение. Если вы представили предел в виде суммы или произведения пределов, то находите их по отдельности, ни в коем случае не объединяя. Если вы получили неопределенность, то надо вернуться и начать с самого начала, но только каким-либо другим способом. Покажем это на следующем примере.

Это неправильный вариант решения!

В конце была получена неопределенность, которую, казалось бы, легко можно раскрыть, воспользовавшись свойством предела суммы наоборот, но, как уже отмечалось, это неверный вариант.

Правильным является признать, что рассмотренный ход решения был неудачным, и попытаться найти другой. Например,

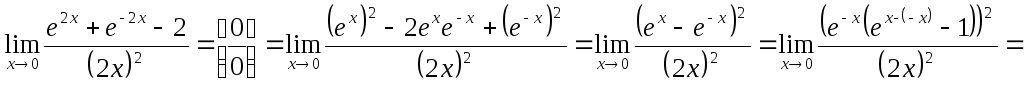
Это правильный ответ.

Задача 12, задача 13. Вычислить пределы функций.

Эти задачи достаточно простые. В них неопределенность либо не встречается, либо легко раскрывается с помощью методов рассмотренных в задачах №9, №10, №11, после которых задачи №12, №13 представляются примитивными. Единственный нюанс, который здесь надо учитывать уже обсуждался в задаче №5 и заключается он в корректном применении свойств пределов. Напоминаем, что среди свойств пределов отсутствует свойство, что . Если решать задачи №12, №13 таким способом ответы будут правильными, но решение некорректным. Поэтому эти пределы требуется решать, используя то, что , а – непрерывные функции, для которых выполняется свойство . В результате имеем:

В полученном выражении пределы находятся аналогично предыдущим задачам, в результате чего получается ответ. Например, . Здесь , , , , . Подставляя найденные пределы в выведенную выше формулу, имеем:

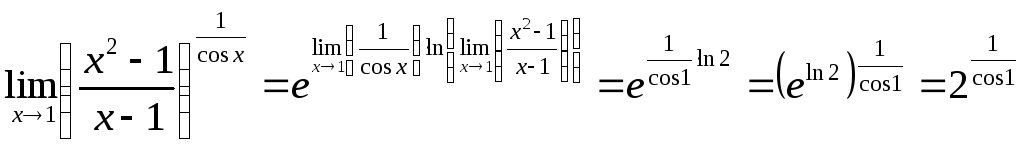
Этот ответ совпадает с ответом, получаемым при неправильном способе решения, поэтому кажется непонятным и ненужным применение правильного способа решения. Приведем простой пример, иллюстрирующий получение ошибки при неправильном способе решения. Рассмотрим второй замечательный предел.

Как видим, получается ошибочное значение. Кстати обращаем ваше внимание, что

, а . В первом случае в бесконечность возводится число, очень близкое к единице, бесконечно приближающееся к единице справа, но не равное единице, поэтому предел равен . Во втором случае в бесконечность возводится число точно равное единице. Так как единица в любой степени равна единице, то предел равен единице. Таким образом, в результате некорректного применения свойств пределов мы бесконечно приближающееся к единице число заменили на число, точно равное единице, что и явилось причиной получения неверного результата.

Решим этот пример корректным способом. Здесь , , , , , поэтому на основании приведенной выше формулы имеем . Получилась неопределенность . Таким образом, правильный способ также не позволил получить ответ, но он корректно дал нам понять, что этот способ нахождения предела неприменим. В связи с этим второй замечательный предел был доказан другим нестандартным способом, поэтому он и получил название замечательный, поскольку не легко было догадаться, как его найти.