
15. Производная по заданному направлению и градиент функции
Ч
Рис. 11
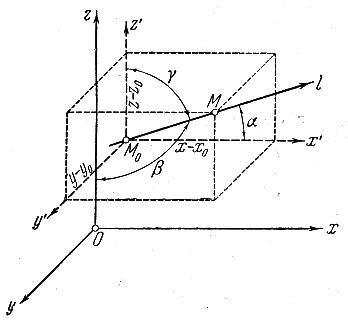
![]() по
по
![]() ,
по
,
по
![]() и по
и по
![]() выражают «скорость изменения» функции
по направлению координатных осей.
Распространим понятие «скорости
изменения функции» по любому заданному
направлению.
выражают «скорость изменения» функции
по направлению координатных осей.
Распространим понятие «скорости
изменения функции» по любому заданному
направлению.
Пусть
![]() определена в некоторой области D.
Рассмотрим любую точку
определена в некоторой области D.
Рассмотрим любую точку
![]() и любую направленную прямую (ось)
и любую направленную прямую (ось)
![]() ,
проходящую через эту точку (рис. 11).
Пусть
,
проходящую через эту точку (рис. 11).
Пусть
![]() произвольная точка этой оси,
произвольная точка этой оси,
![]() длина отрезка между двумя точками,
взятая со знаком «+», если направление
длина отрезка между двумя точками,
взятая со знаком «+», если направление
![]() совпадает с направлением оси
совпадает с направлением оси
![]() ,
и со знаком минус – в противном случае.
,
и со знаком минус – в противном случае.
Предел
![]()
называется
производной от функции
![]() по направлению
по направлению
![]() (или вдоль оси
(или вдоль оси
![]() )
в точке
)
в точке
![]() и обозначается следующим образом:
и обозначается следующим образом:
![]() .
.
Эта
производная характеризует «скорость
изменения» функции
![]() в точке
в точке
![]() по направлению
по направлению
![]() .
.
Если
ось
![]() образует с осями координат углы
образует с осями координат углы
![]() ,
,
![]() и
и
![]() ,
то единичный вектор
,
то единичный вектор
![]() по направлению
по направлению
![]() имеет координаты
имеет координаты
![]() .
В случае, если функция
.
В случае, если функция
![]() имеет в рассматриваемой области
непрерывные частные производные,
производная по направлению
имеет в рассматриваемой области
непрерывные частные производные,
производная по направлению
![]() выражается формулой
выражается формулой
![]() .
.
Градиентом функции
![]() называется вектор
называется вектор
![]() ,
координатами которого являются частные
производные функции:
,
координатами которого являются частные
производные функции:
![]() .
.
Справедлива следующая
формула, представляющая производную
по направлению в виде скалярного
произведения векторов
![]() и градиента функции
и градиента функции
![]() :
:
![]() .
.
По определению
скалярного произведения, помня, что
![]() ,
имеем
,
имеем
![]() ,
,
![]() ,
,
где
![]() – угол между векторами
– угол между векторами
![]() и
и
![]() .
.
Из
последнего равенства следует, что
производная функции по направлению
имеет наибольшую величину, когда
![]() ,
т.е. когда угол между этими векторами
равен нулю. Иными словами, когда
направление
,
т.е. когда угол между этими векторами
равен нулю. Иными словами, когда
направление
![]() совпадает с направлением градиента
функции. При этом
совпадает с направлением градиента
функции. При этом
![]() .
(13)
.
(13)
(![]() – единичный вектор по направлению
– единичный вектор по направлению
![]() ).
).
Таким образом, градиент
функции в каждой точке указывает
направление максимальной скорости
возрастания этой функции в данной точке,
а его длина
![]() – величину скорости возрастания.
– величину скорости возрастания.
Понятия производной по направлению и градиента функции используются во многих приложениях.
Пример
11. Найти производную от функции
![]() в точке
в точке
![]() в направлении градиента.
в направлении градиента.
Решение. Найдем
частные производные функции в точке
![]() и составим вектор градиента функции в
этой точке:
и составим вектор градиента функции в
этой точке:
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
Найдем единичный вектор данного направления:
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() .
.
Тогда
![]() .
.
Мы на примере убедились в справедливости формулы (13).
16. Дифференцирование неявных функций
Часто функция одной
или нескольких переменных бывает задана
неявно. Функция
![]() называется неявной, если она задана
с помощью неразрешенного
относительно
называется неявной, если она задана
с помощью неразрешенного
относительно
![]() уравнения
уравнения
![]() .
(14)
.
(14)
Она становится явной,
если рассматривается непосредственная
зависимость
![]() от
от
![]() .
Иначе говоря, под явным заданием функции
подразумевается задание функции с
помощью конкретного аналитического
выражения.
.
Иначе говоря, под явным заданием функции
подразумевается задание функции с
помощью конкретного аналитического
выражения.
Приведем несколько примеров. При соответствующих ограничениях на независимые переменные неявным заданием функции
-
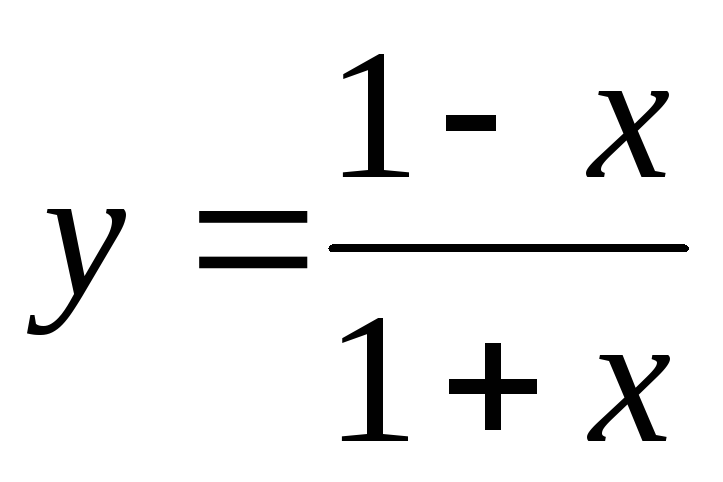 может служить уравнение
может служить уравнение
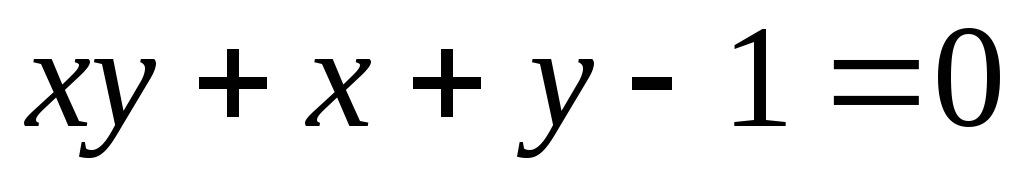 ,
, -
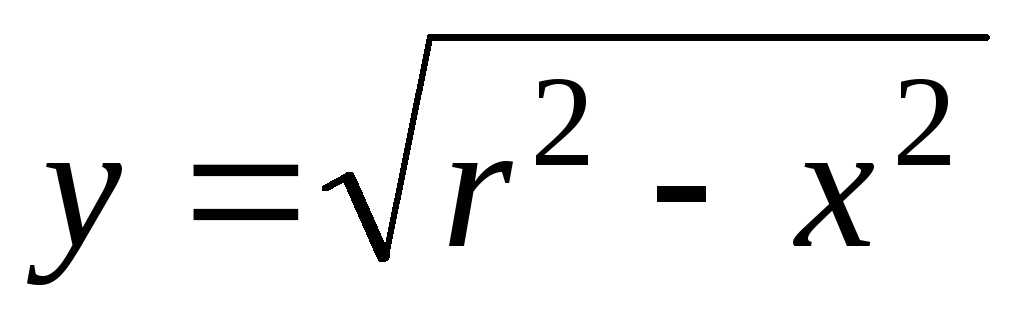 – уравнение
– уравнение
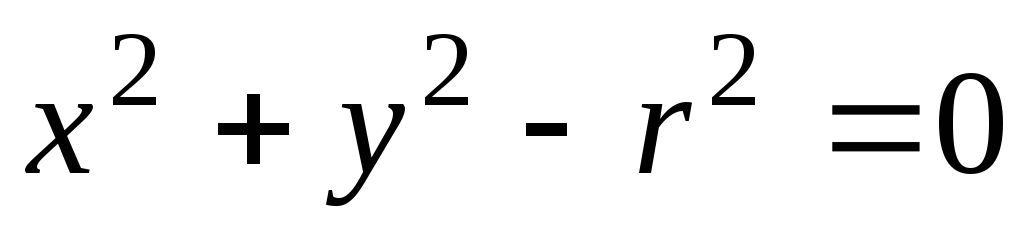 ,
, -
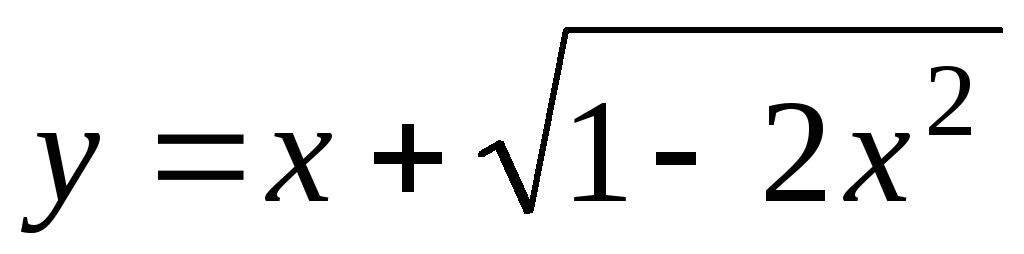 – уравнение
– уравнение
 .
.
Но не всякое уравнение легко разрешить относительно одной из переменных. Более того, существует много уравнений, которые мы, несмотря на огромный прогресс математики, до сих пор не можем решить. Кроме того, не следует думать, что если дано некоторое уравнение, связывающее несколько переменных, то тем самым уже определена некоторая неявная функция. В действительности может не существовать ни одной непрерывной функции, удовлетворяющей заданному уравнению, или может существовать несколько таких функций. Например:
-
Не существует ни одной функции действительной переменной, удовлетворяющей уравнению
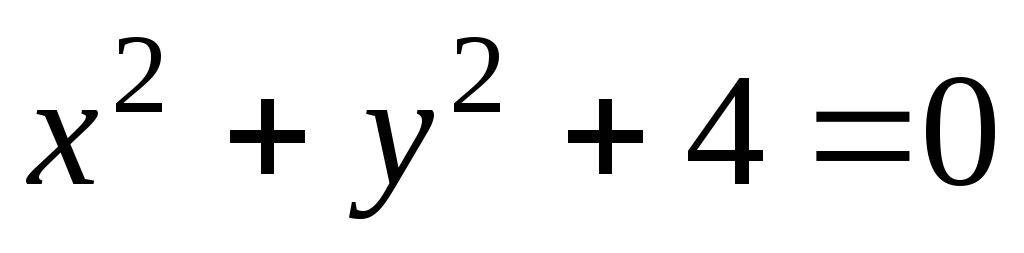 .
. -
Функции
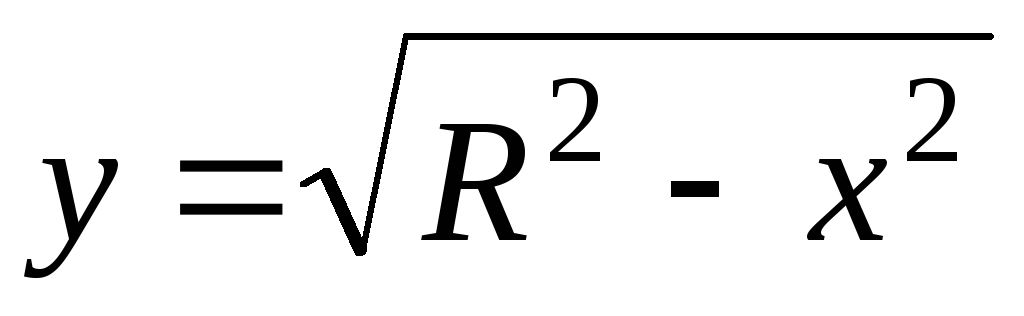 и
и
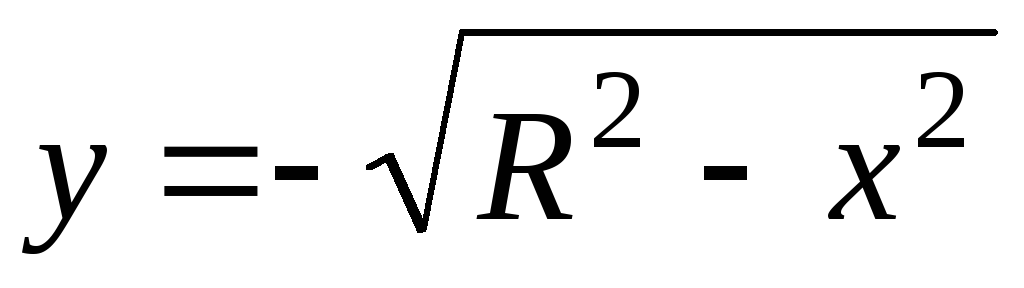 удовлетворяют одному и тому же уравнению,
а именно:
удовлетворяют одному и тому же уравнению,
а именно:
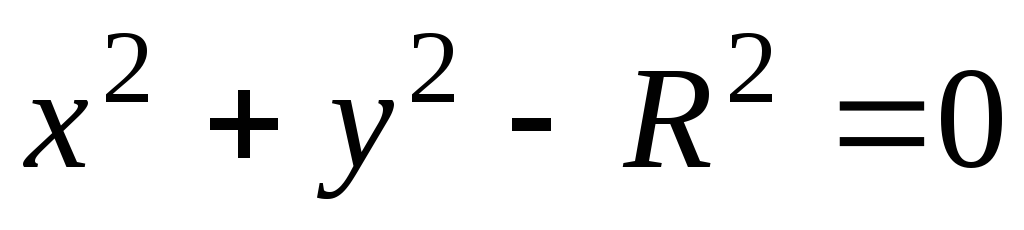 .
.
Теорема о неявной функции. Если
-
функция
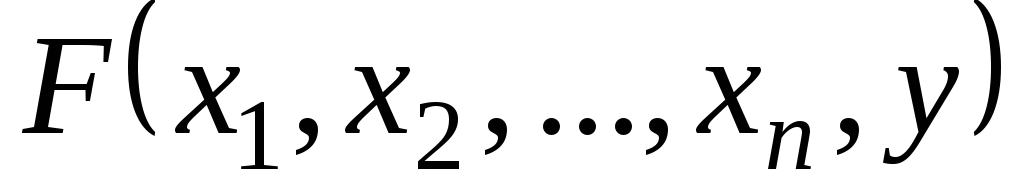 определена и непрерывна в
определена и непрерывна в
 параллелепипеде
параллелепипеде
![]() ,
,
с центром в точке
![]() ;
;
-
частные производные
 существуют и непрерывны в
существуют и непрерывны в
 ;
; -
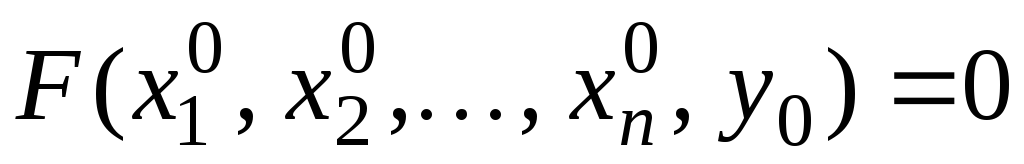 ;
; -
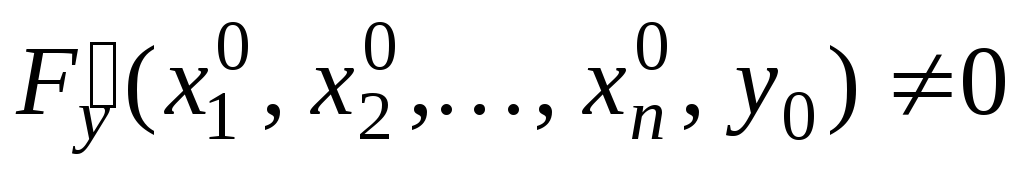 ,
,
то
-
в некоторой окрестности точки
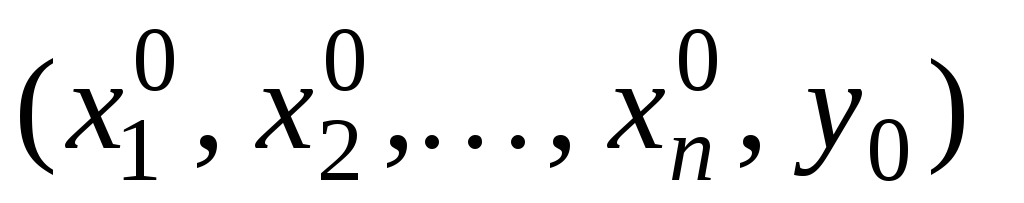 уравнение (14) определяет
уравнение (14) определяет
 как однозначную функцию от
как однозначную функцию от
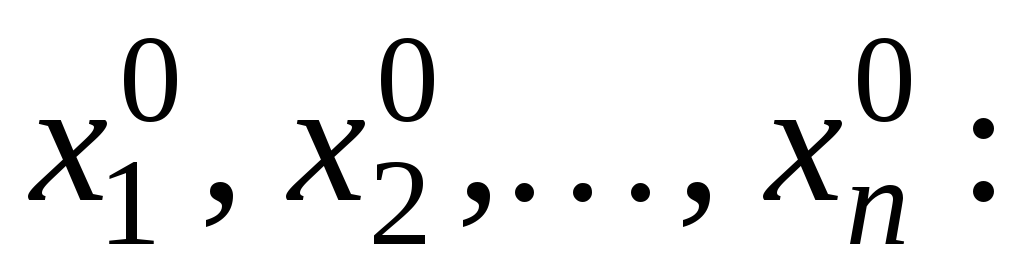
![]() ;
;
-
при
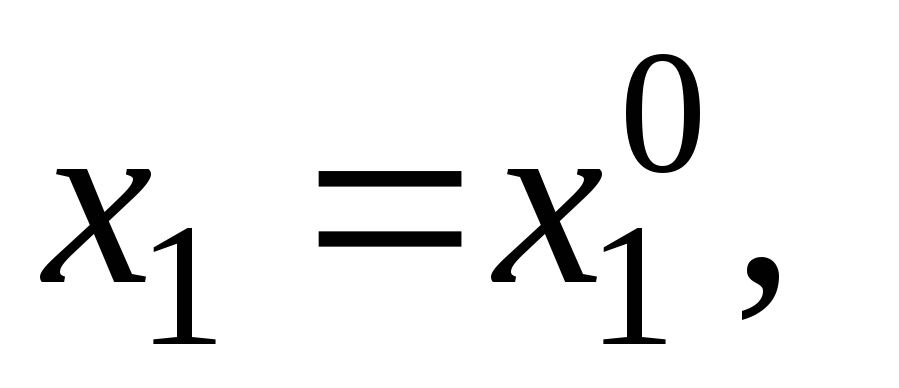
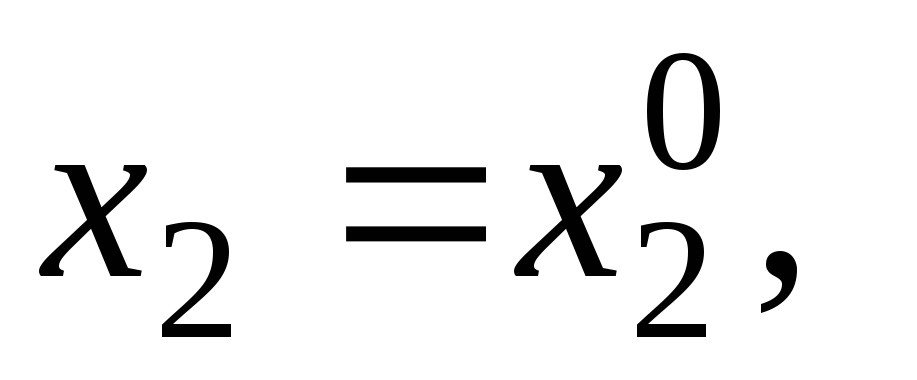 …,
…,
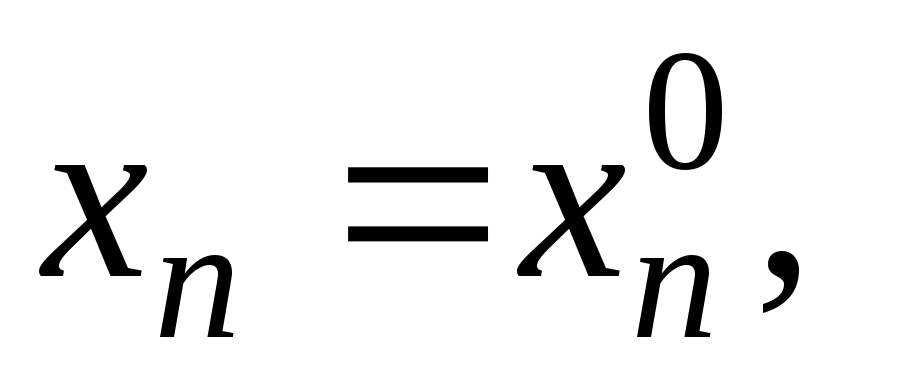 эта функция принимает значение
эта функция принимает значение
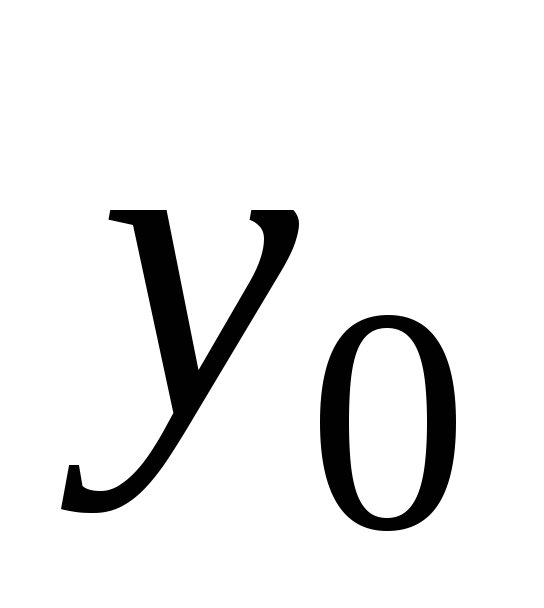 ,
т.е.
,
т.е.
 ;
; -
функция
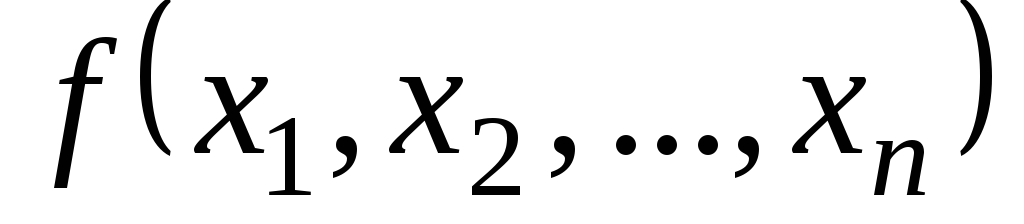 непрерывна по совокупности своих
аргументов и
непрерывна по совокупности своих
аргументов и -
имеет непрерывные частные производные
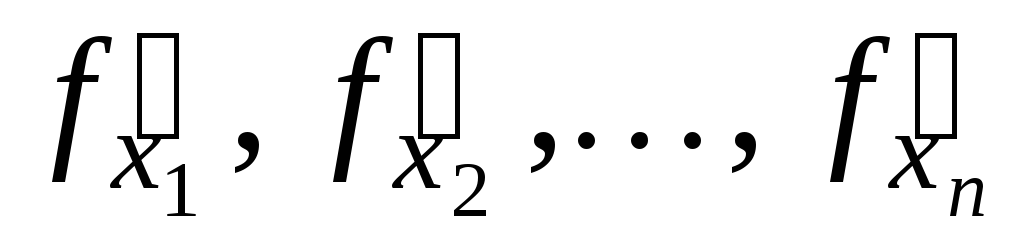 .
.
Пример. Пусть
![]()
Эта функция определена
и непрерывна на всей плоскости
![]() .
Частные производные
.
Частные производные
![]()
тоже существуют и непрерывны всюду.
Выбрав
в качестве
![]() точку
точку
![]() ,
получим:
,
получим:
![]()
![]() .
.
Следовательно, по теореме о
неявной функции, в окрестности точки
![]() существует одна и только одна функция
существует одна и только одна функция
![]() ,
удовлетворяющая уравнению
,
удовлетворяющая уравнению
![]() ,
принимающая в этой точке значение
,
принимающая в этой точке значение
![]() ,
непрерывная в ней и имеющая непрерывную
производную
,
непрерывная в ней и имеющая непрерывную
производную
![]() .
.
То же самое можно сказать и о
любой другой точке
![]() ,
удовлетворяющей условиям
,
удовлетворяющей условиям
![]() ,
,
![]() .
.
Замечание. Необходимо обратить внимание на локальный характер теоремы о неявной функции: речь все время идет лишь о некоторой окрестности рассматриваемой точки.
Для того чтобы найти производную или частные производные неявной функции, есть несколько способов. Один из них – это предварительно привести её к явному виду, т.е. разрешить относительно данной функции то уравнение, которое её определяет.
Другой – простой и сравнительно лёгкий путь, когда можно обойтись без предварительного решения уравнения, задающего неявную функцию.
Пусть
выполняются условия теоремы о неявной
функции. Тогда функция
![]() имеет частные производные, вычисляемые
по формуле:
имеет частные производные, вычисляемые
по формуле:
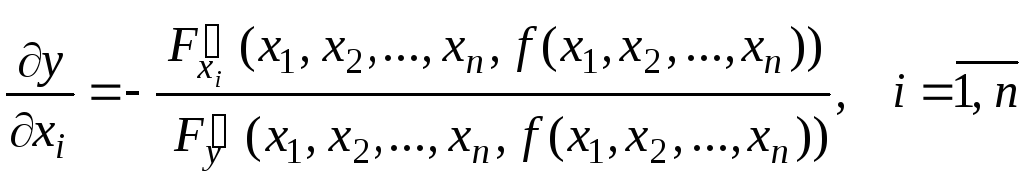 .
(15)
.
(15)
Есть еще один способ для нахождения частных производных неявной функции. Если нужны все частные производные первого (второго, третьего,…) порядка, то проще сразу вычислять полные дифференциалы первого (второго, третьего,…) порядка от левой части уравнения (14) и приравнивать их нулю:
![]() ,
(16)
,
(16)
откуда получаем
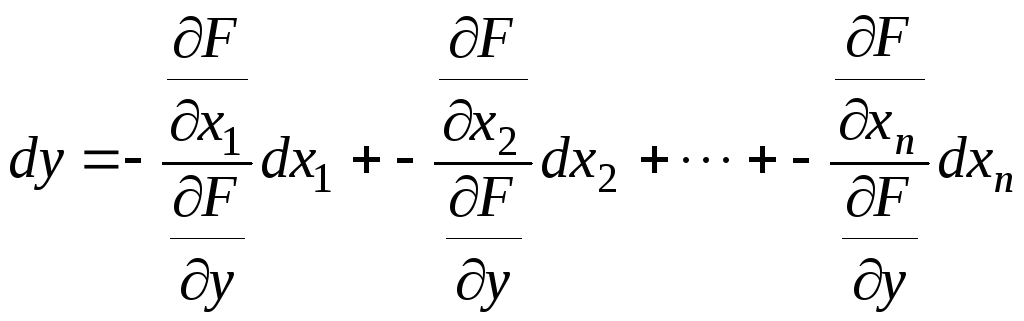 .
.
В то же время
![]() ,
,
откуда
и получим, в силу произвольности
![]() ,
формулы (15).
,
формулы (15).
Дифференцируя
еще раз уравнение (16), определим
дифференциал второго порядка искомой
функции, что приведет нас к выражениям
для частных производных второго порядка
и т.д. Заметим, что во всех производимых
выкладках здесь необходимо должно
выполняться условие, что
![]() .
.
Пример
12. Найти производную
![]() по
по
![]() ,
если
,
если
![]() .
.
Решение. Решать
это уравнение относительно
![]() затруднительно, т.к. оно третьей степени
относительно
затруднительно, т.к. оно третьей степени
относительно
![]() .
Воспользуемся вышеприведёнными теоремой
и формулой (15), где
.
Воспользуемся вышеприведёнными теоремой
и формулой (15), где
![]() .
.
Эта функция определена
и непрерывна на всей плоскости
![]() .
Частные производные
.
Частные производные
![]()
тоже существуют и непрерывны всюду.
Уравнение
![]() имеет два решения:
имеет два решения:
![]() и
и
![]() ,
,
причем
![]() ,
а
,
а
![]() .
.
Следовательно, функция
![]() удовлетворяет условиям теоремы о
неявной функции только в некоторой
окрестности точки
удовлетворяет условиям теоремы о
неявной функции только в некоторой
окрестности точки
![]() .
Поэтому в окрестности этой точки
существует однозначная функция
.
Поэтому в окрестности этой точки
существует однозначная функция
![]() и ее производная:
и ее производная:
![]()
Пример
13. Найти частные производные и полный
дифференциал функции
![]() ,
заданной неявно выражением
,
заданной неявно выражением
![]() .
.
Решение.
![]()
![]()
А полный дифференциал запишется в следующем виде:
![]() .
.
Пример
14. Найти частные производные и полный
дифференциал функции
![]() ,
заданной неявно выражением
,
заданной неявно выражением
![]() .
.
Решение. Дифференцируем обе части заданного уравнения:
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() .
.
Пример 15. Найти
частные производные второго порядка
функции
![]() ,
заданной неявно уравнением
,
заданной неявно уравнением
![]() .
.
Решение. Дифференцируем обе части заданного уравнения:
![]() ,
(a)
,
(a)
![]()
![]() (b)
(b)
![]()
![]() .
.
![]() .
.
Дифференцируем еще раз, теперь уравнение (a):
![]() .
(с)
.
(с)
Воспользовавшись уже
известным выражением (b)
для
![]() ,
получим:
,
получим:
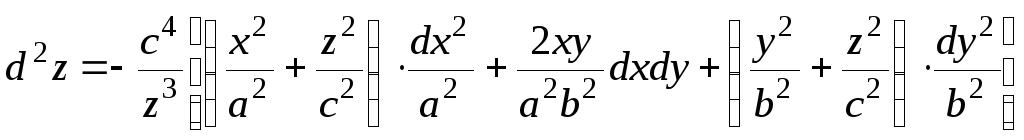
![]()
![]()
![]()
![]() .
.
Чтобы
получить производные третьего порядка,
дифференцируем полученное уравнение
(c) еще раз. Подставив в
полученное выражения для дифференциалов
первого и второго порядков, решим его
относительно дифференциала третьего
порядка, откуда легко выпишем все частные
производные третьего порядка от функции
![]() ,
заданной неявно.
,
заданной неявно.
