Лекция 21

5.7.Скалярный и векторный потенциалы электромагнитного поля

Мы показали, что ротор магнитного поля отличен от нуля. Такое поле нельзя описывать потенциалом φ, так как оно непотенциально, работа по замкнутому контуру сил поля отлична от нуля.

Для описания магнитного поля вводят векторный потенциал , причем

(5.13)

Векторный потенциал , также как и скалярныйφ, определяется неоднозначно. Для однозначного его определения необходимо задать граничные условия.

Подобно уравнению Пуассона для скалярного потенциала φ(), запишем уравнение для векторного потенциаладля поля постоянного тока. В выражение для закона полного тока в дифференциальной форме

подставим , учитывая, что для постоянного тока,. Имеем:

.

Известно из математики, что Дивергенция от ротора равна нулю,, тогда, или

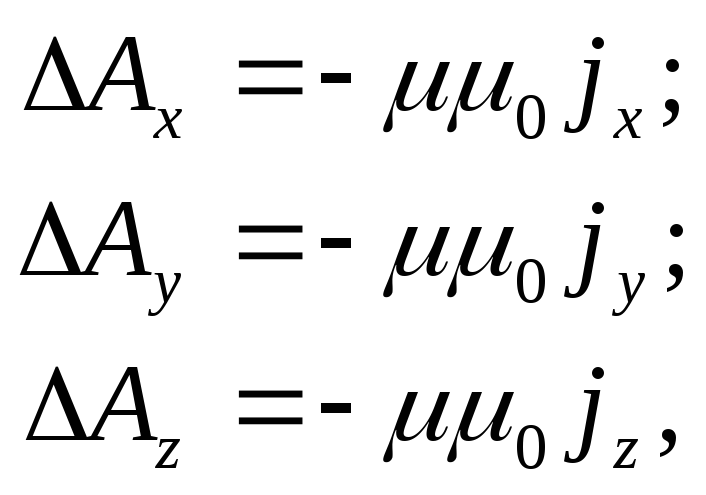
где - оператор Лапласа.

Подставим выражение (5.13) в уравнение Максвелла для :

Это соотношение можно переписать в виде

Так как ротор вектора равен нулю, этот вектор можно представить в виде градиента некоторой функцииφ:

Функция φназывается скалярным потенциалом электромагнитного поля. В нестационарном случае она зависит от радиус-вектора точкии времениt. Потенциалыφ и имеют одинаковую размерность.

Таким образом, напряженность электрического поля в общем случае определяется не только скалярным потенциалом φ,но и векторным потенциалом

(5.14)

Второе слагаемое обусловлено явлением электромагнитной индукции. В случае стационарного поля=0, и выражение (5.14) переходит в известное в электростатике

Найдем уравнения, с помощью которых можно вычислить потенциалы иφ для поля в однородной и изотропной среде с постоянными диэлектрическойεи магнитной проницаемостьюμ.Возьмем второе уравнение Максвелла

где - скорость света в среде, имеем

Из третьего уравнения Максвелла . Подставими:

Но, учитывая, что и, имеем

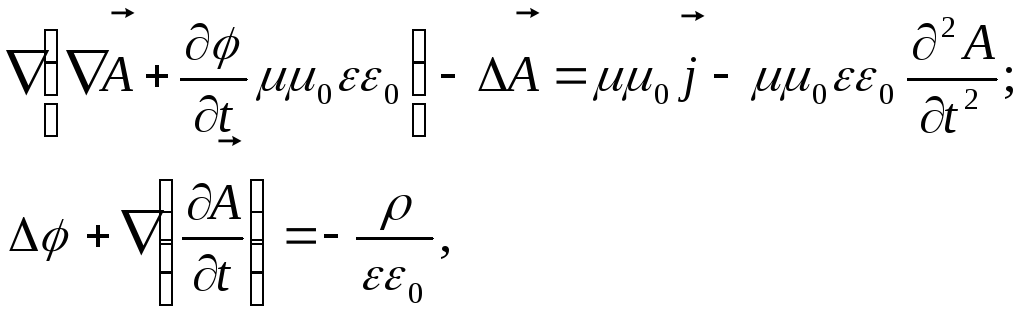
или

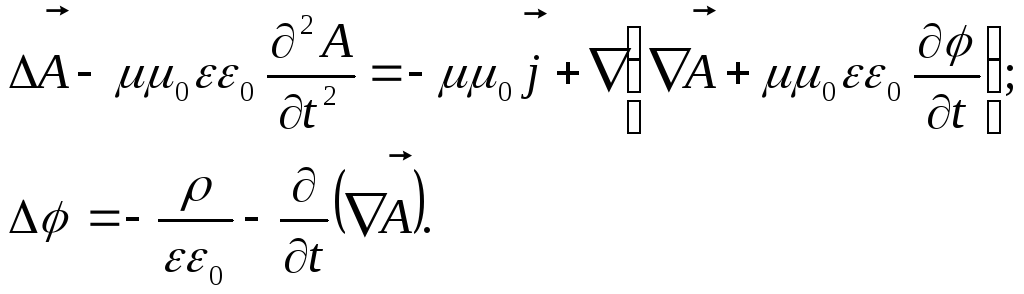(5.15)

Уравнения (5.15) – это и есть искомые уравнения для и φ.

Потенциалы и φопределяются неоднозначно, поэтому имеется некоторая свобода в их выборе. В частности, например, к можно прибавить произвольный постоянный вектор , а кφ- произвольную постоянную без того, чтобы изменились значенияи . Выбор потенциалов следует осуществлять наиболее удобным для данного случая образом. Такойнаиболее целесообразный выбор потенциалов называется их калибровкой.

Рассмотрим самый общий вид калибровочных преобразований потенциалов и φ, при которых поляиостаются неизменными. Полене изменится, если кдобавить градиент произвольной скалярной функцииf (ротор градиента равен нулю), т.е. перейти отк

(5.16)

Чтобы при этом не изменилось электрическое поле (), нужно совершить переход отφ кφ΄

(5.17)

где f - та же функция. Поле, определяемое потенциаламиφ΄ и, в этом случае равно

.

Здесь использовано

Таким образом, эти преобразования не меняют полей и. Все уравнения, описывающие поля, должны быть инвариантными по отношению к калибровочным преобразованиям. Эта инвариантность называется калибровочной или градиентной инвариантностью.

На практике часто применяется калибровка, называемая условием Лоренца:

(5.18)

Для поля в вакууме условие Лоренца принимает вид:

Покажем, что условие (5.18) может быть удовлетворено надлежащим выбором функции f в формулах (5.16) и (5.17). Для этого подставим в уравнение (6) значенияφ΄ и, определяемые этими формулами:

здесь Получаем уравнение для нахождения функцииf

где - есть заданная функцияиt. Подставив функциюf, получающуюся из решения этого уравнения, в формулы (5.16) и (5.17), мы найдем значения потенциаловφ΄ и, удовлетворяющие условию (5.18).

Условие Лоренца сильно ограничивает набор значений потенциалов, пригодных для описания данного поля, но все же не делает выбор потенциалов вполне однозначным. Действительно, не нарушая условия (5.18), можно осуществить преобразования

(5.19)

при этом оба набора потенциалов предполагаются удовлетворяющими условию Лоренца. Функция ψ является решением уравнения

(5.20)

Действительно, подставив в левую часть выражения (5.18) вместо иφ штрихованные потенциалы из (5.19), получим выражение

которое согласно (5.18) и (5.20) равно нулю. Таким образом, если иφ принадлежат к лоренцевой калибровке, то и определяемые преобразованиями (5.19) потенциалыиφ` принадлежат той же калибровке. Это обстоятельство позволяет наложить на потенциалы кроме условия (5.18) еще одно дополнительное условие. Например, можно потребовать, чтобы. Для этого, согласно второму из уравнений (5.18), достаточно выбрать функциюψтак, чтобы ее производная по времени была равнаφ.

В качестве дополнительного условия также может быть принято требование

(5.21)

Из (5.19) следует, что поэтому для выполнения требованиянеобходимо соблюдение равенстваместе с тем, из (5.20) имеемпоэтому, если взять в качествеψрешение уравненияи подставить это решение в (5.19), мы получим значения потенциаловφ΄ и, удовлетворяющие и условию Лоренца, и требованию (5.21).

Лоренцева калибровка, удовлетворяющая дополнительному условию (5.21) называется кулоновской или поперечной калибровкой. В случае этой калибровки скалярный потенциал удовлетворяет уравнению Пуассона

т.е. является кулоновским потенциалом (отсюда и название «кулоновская калибровка»).