1. Идеальные и реальные источники напряжения и тока, условия согласования с нагрузкой. Зависимости мощности и кпд от нагрузки.

• Реальный источник напряжения – источник в котором при изменении нагрузки напряжения на выходных клеммах изменяется незначительно. Это вызвано тем, что такой источник электроэнергии имеет некоторое внутреннее сопротивление - малой величины.

• Идеальный источник напряжения – источник который при изменении нагрузки сохраняет постоянную величину напряжения на выходных клеммах, равное ЭДС.

• Источник энергии – характеризуется постоянством тока в нагрузке при ее изменении. Это достигается тем. Что внутренее сопротивление источника тока очень велико. Действительно, если Re >> Rн то, величена тока Iн не зависит от величины Rн и ею можно пренебречь

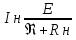
• Идеальный источник тока – при изменении нагрузки сохраняет постоянной величину тока нагрузки. Внутреннее сопротивление идеального источника тока равно бесконечности.

• Реальный источник тока – источник, который имеет высокое, конечное внутреннее сопротивление.

Условие согласования – при подключении нагрузки к реальному источнику напряжения необходимо, чтобы в нагрузку передавалась максимальная мощность. Этот режим называется согласованным, а условие, при котором он имеет место, называют условием согласования.

Мощность, потребляемая нагрузкой (рис. 1.23), равна:

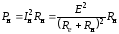(1.1)

Из полученного выражения видно, что при R_н = 0 мощность нагрузки P_н = 0, а при R_н =  мощность нагрузки также P_н = 0. Очевидно, изменяя R_н, это выражение при определенной величине R_н будет иметь максимальное значение (экстремум). Для определения экстремальной точки возьмем производную от P_н по R_н и приравняем к нулю:

.

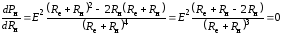R_e = R_н. (1.2)

Итак, если величина нагрузки R_н равна внутреннему сопротивлению R_е источника напряжения, то в нагрузку будет передаваться максимальная мощность P_н.max. Это и есть условие согласования источника напряжения с нагрузкой.

Величина максимальной мощности определится, если в выражение (1.1) подставить условие согласования источника напряжения с нагрузкой (1.2):

. (1.3)

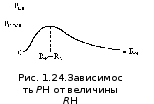На рис. 1.24 показана зависимость Р_н при изменении R_н. Рассмотрим как изменяется коэффициент полезного действия КПД реального источника напряжения при изменении нагрузки.

При изменении нагрузки R_н изменяется величина тока I_н . Это приводит к изменению мощности, выделяемой в источнике на его внутреннем сопротивлении R_н. В результате происходит перераспределение мощности источника между его внутренним сопротивлением нагрузкой. Такое перераспределение можно оценить с помощью коэффициента полезного действия источника.

Рассмотрим изменение КПД реального источника напряжения при изменении нагрузки. Под КПД (условное обозначение – ) источника напряжения понимается отношение мощности нагрузки Р_н к мощности источника Р_ист.

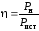. (1.4)

Определим мощность, выделяемую источником:

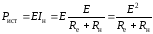. (1.5)

Подставим в (1.4) найденное выражение для P_ист (1.5) и для P_н (1.1):

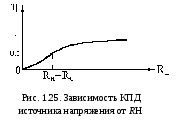
.(1.6)

На рис. 1.25 показана зависимость КПД от R_н.

При условии согласования (1.2) КПД равно:

.

2. Синусоидальный ток и напряжение в комплексной форме. Векторная диаграмма, комплексное сопротивление, треугольник сопротивлений. Мощности при гармоническом напряжении и токе, добротность и затухание.

Под синусоидальным током понимается ток моногармонической формы, т. е. ток в виде гармонической функции (синусоидальное или косинусоидальное представление) с определенной частотой и определенной начальной фазой.

При расчете электрической цепи используются гармонические функции sin – ой или cos–ой формы. Так переменное напряжение в sin–ой форме может иметь вид:

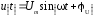. (2.1)

Переменный ток в cos–ой форме имеет вид:

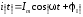, (2.2)

где U_m, I_m– амплитуды напряжения и тока, _U, _I – начальные (при t = 0) фазы напряжения и тока,  – круговая частота.

Несмотря на относительную простоту этих функций, аналитические операции над ними и графическое представление на одном графике несколько таких функций вызывает определенные сложности.

От этих сложностей свободен метод комплексных амплитуд, предложенный американскими инженерами А. Е. Кеннели и П. Ч. Штейнметцом в 1893–1894 гг.

Он основан на том, что показательная функция от комплексного аргумента j обладает периодичностью. На основе формулы Эйлера имеем:

.

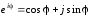Введем понятие комплексного напряжения:

. (2.3)

Видно, что мнимая часть комплексного выражения полностью совпадает с переменным напряжением в sin–ой форме (2.1). Сразу отметим, что если бы переменное напряжение было представлено в cos–ой форме, то оно совпало бы с вещественной частью комплексного напряжения.

Введем понятие комплексного тока:

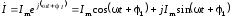. (2.4)

Здесь вещественная часть комплексного выражения совпадает с переменным током в cos–ой форме (2.2). Если бы в (2.2) была sin–ая форма, то она совпала бы с мнимой частью комплексного тока.

Было предложено периодический сигнал представлять в комплексной форме (2.3), (2.4). Так как вещественная часть комплексного сигнала имеет cos–ый характер, то целесообразно исходные сигналы записывать в cos–ой форме (в принципе cos–ая и sin–ая функции отличаются только фазой).

Возникает мысль, что тогда в процессе анализа необходимо все время подчеркивать, что в комплексном токе или напряжении учитывается только вещественная составляющая. Однако, в процессе анализа этого делать нет необходимости, а делается это только в конце анализа в результатах расчета.

Итак, в методе комплексных амплитуд исходное переменное напряжение в начале записывается в cos–ой форме:

.

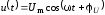Затем это напряжение представляется в комплексной форме:

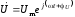. (2.5)

В такой форме записываются напряжения и токи цепи, выполняется анализ, получается результат в комплексной форме, вещественная часть которого и будет действительным результатом.

Запишем комплексное напряжение и комплексный ток:

,

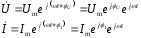Здесь и 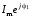называются комплексными амплитудами напряжения и тока и обозначаются:

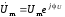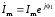; . (2.6)

Комплексные амплитуды напряжения и тока – это значение комплексных напряжения и тока при t = 0.

Всякая комплексная величина может быть представлена вектором на комплексной плоскости. Если аргумент комплексной величины зависит от времени, например (2.5), то на комплексной плоскости эта величина должна представляться вектором, вращающимся против часовой стрелки (положительное направление вращения) с частотой ω. Реально отобразить это на комплексной плоскости не возможно. Поэтому такая комплексная величина на комплексной плоскости представляется в виде вектора при

t = 0. На рис. 2.1 показаны вектора напряжения и тока в комплексной форме на комплексной плоскости.

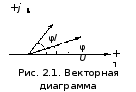Комплексная плоскость, на которой представлены вектора комплексных напряжений и токов называется векторной диаграммой.

Законы Кирхгофа для комплексных токов имеют такую же трактовку, как и для цепей постоянного тока. В цепях переменного тока помимо резисторов большую роль играют реактивные элементы – конденсаторы и катушки индуктивности. Они так же формируют сопротивление цепи. При использовании комплексных напряжений и токов вводится понятие комплексного сопротивления, которое обозначается . Закон Ома в комплексной форме имеет вид:

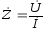. (2.7)

Как всякая комплексная величина, комплексное сопротивление cостоит из вещественной и мнимой частей:

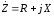. (2.8)

Такое представление комплексного сопротивления принято называть алгебраической формой представления.

Вещественная часть R комплексного сопротивления цепи переменного тока включает резистивные (диссипативные) составляющие цепи. Мнимая часть X комплексного сопротивления переменного тока включает реактивные составляющие цепи. Поэтому она называется чаще реактивной составляющей комплексного сопротивления. Если вещественная часть комплексного сопротивления всегда положительная, то реактивная часть может быть положительной (X>0) или отрицательной (X<0).

Комплексное сопротивление иногда удобно представлять в тригонометрической и показательной формах:

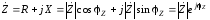, (2.9)

где; .

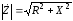Комплексное сопротивление может быть представлено на комплексной плоскости (рис. 2.2) в виде отрезка, проведенного под углом _Z к вещественной оси.

Проекции комплексного сопротивления на оси комплексной плоскости, соединенные в виде треугольника, создают треугольник сопротивлений. Из треугольника сопротивления можно получить выражения для модуля и фазы сопротивления (2.9), а так же косинусоидальную и синусоидальную составляющие в тригонометрической форме представления комплексного сопротивления.

. Мощности при гармоническом напряжении и токе.

Добротность и затухание

В электронных цепях понятие мощности находит очень широкое применение. Мы интересуемся мощностью входного и выходного сигналов усилительного устройства. Необходимо знать, какая мощность рассеивается на резисторе, чтобы выбрать соответствующий резистор и т. д.

Рассмотрим понятие мгновенной мощности P(t). Допустим, по некоторому участку цепи протекает переменный ток с нулевой фазой ( = 0):

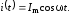
Ток создает падение напряжения на данном участке цепи. В общем случае его фаза отличается от фазы тока на некоторый угол :

.

Мгновенной мощностью называется произведение мгновенного напряжения на мгновенный ток:

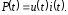(2.10)

Подставим в (2.10) значения напряжения и тока и выполним очевидные преобразования:

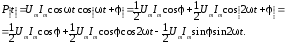(2.11)

Найдем комплексное сопротивление цепи. Для этого представим в комплексной форме напряжение и ток.

С учётом этого определяем комплексное сопротивление по закону Ома:

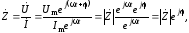(2.12)

где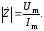

Найденное комплексное сопротивление цепи представлено в показательной форме. Выразим его в тригонометрической и алгебраической формах:

Приравнивая вещественные и мнимые составляющие тригонометрического и алгебраического представления комплексного сопротивления, находим:

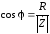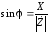, . (2.13)

Эти же соотношения получаются из треугольника сопротивления (рис. 2.2).

Подставим (2.13) в последнее выражение для мгновенной мощности (2.11):

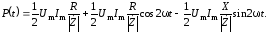
Из (2.12) находим:

.

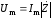и подставляем в последнее выражение для мгновенной мощности

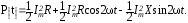(2.14)

Электрические процессы, связанные с резисторами, характеризуются диссипацией энергии, активным потреблением мощности. Этому соответствует первых два слагаемых в (2.14), т. к. в них присутствуют резисторы. Эту часть принято называть мгновенной активной мощностью и обозначать как P_акт:

(2.15)

Электрические процессы, связанные с реактивными элементами, характеризуются накоплением энергии и затем передачи ее. Это называется реактивным потреблением энергии. Такое свойство цепи описывается третьим слагаемым мгновенной мощности (2.14), т. к. в нем присутствует только реактивное сопротивление X. Эту часть мгновенной мощности принято называть мгновенной реактивной мощностью и обозначать как P_реак:

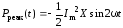. (2.16)

Часто интерес представляет не значение мощности в конкретный момент времени, а среднее значение мгновенной мощности за период T. Эта мощность называется средней мощностью и определяется по формуле:

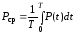. (2.17)

Подставляем в (2.17) выражение для мгновенной мощности (2.11). Учитывая, что интеграл от гармонической функции на периоде равен нулю, получаем:

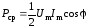. (2.18)

Выразим cos, с учетом (2.13) и (2.12), через сопротивление резистора, ток и напряжение.

(2.19)

Подставив (2.19) в выражение средней мощности (2.18), находим:

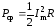. (2.20)

Из выражения (2.20) видно, что потребление мощности осуществляется только резистором, величина которой пропорциональна величине резистора и квадрату тока, протекающего через него.

На практике при определении мощности используются не амплитудные, а действующие значения напряжения и тока (U_д, I_д), которые связаны между собой следующим соотношением:

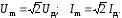
(2.21)

Подставляя (2.21) в (2.18) и (2.20), выразим значение средней мощности P_cр через действующие значения напряжения и тока:

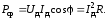(2.22)

При оценке определённых свойств радиотехнических элементов (катушки индуктивности, конденсаторы) и радиотехнических узлов (резонансные контура и др.) используются понятия добротности и затухания.

Добротностью называется отношение амплитуды реактивной мощности цепи к величине средней мощности.

Добротность цепи обозначается через Q. Исходя из определения, делим амплитуду реактивной мощности (2.16) на выражение для средней мощности (2.18):

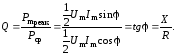
(2.23)

Последнее соотношение получено из треугольника сопротивлений (рис. 2.2).

В дальнейшем мы увидим, что чем больше добротность, тем дольше сохраняются в цепи колебательные процессы. Это просматривается из последнего выражения (2.23). Действительно, чем меньше R, тем меньше рассеивание (диссипация) мощности, тем дольше идут колебательные процессы.

Затуханием называется величина, обратная добротности, и обозначается через d.