Лекция 4-5

4. Зонная теория твердого тела

4.1. Уравнение Шредингера для твердого тела

Любое твердое тело состоит из атомов, т.е. представляет собой совокупность ядер и электронов. В кристаллических твердых телах ядра атомов располагаются в узлах кристаллической решетки, обладающей пространственной периодичностью.

Стационарные состояния всех частиц описываются уравнением Шредингера:

, (4.1)

где - гамильтониан всей совокупности частиц,-собственная волновая функция;Е - энергия твердого тела.

Обозначим ₁,₂ …- радиус-векторы электронов, а₁,₂…- радиус-векторы ядер. ПустьМ_к- масса ядра атома видак,m -масса электрона.

Гамильтониан системы частиц , где- оператор кинетической энергии,U– потенциальная энергия системы,

.

Здесь - оператор Лапласа дляi –той частицы. Первое слагаемое представляет собой оператор кинетической энергии электронов, второе – ядер.

Потенциальная энергия совокупности частиц, составляющих твердое тело - это энергия попарного взаимодействия электронов с электронами, ядер с ядрами и электронов с ядрами:

.

Волновая функция зависит от координат всех частиц:

.

Если на эту волновую функцию наложить ограничения, вытекающие из ее физического смысла (конечность, однозначность, непрерывность), то уравнение Шредингера будет иметь решение не при любых значениях энергии Е, а лишь при некоторых. Эти значенияЕявляются решением уравнения (4.1) и определяют энергетический спектр твердого тела.

Из-за огромного числа независимых переменных уравнение (4.1) не имеет точного решения. Для описания приближенного решения прибегают к ряду упрощений:

- Ядра в кристаллах совершают колебания относительно своих положений равновесия. Электроны же участвуют в поступательно – вращательном движении, при этом их скорость много больше скорости ядер. Приближение, учитывающее различный характер движения ядер и электронов, называется адиабатическим приближением (или приближением Борна- Оппенгеймера).

Самое грубое допущение состоит в том, что ядра покоятся. Тогда уравнение (4.1) принимает вид:

. (4.2)

Оно описывает движение электронов в поле неподвижных ядер.

- Валентная аппроксимация. Считают, что все электроны внутренних оболочек атома образуют вместе с ядром покоящегося атома атомный остаток, то есть ион, и уравнение (4.2) записывают лишь для валентных электронов, которые движутся в некотором результирующем поле неподвижных ионов.

4.2. Одноэлектронное приближение

Многоэлектронная задача (решение уравнения (4.2)) может быть сведена к одноэлектронной. Для этого используют метод Харти-Фока, который состоит в замене потенциальной энергии взаимодействия электронов в уравнении (4.2) потенциальной энергией вида , представляющей собой энергию взаимодействияi-го электрона с некоторым эффективным полем, в котором каждый электрон движется независимо. Это поле характеризует действие всех остальных электронов на i – ый электрон. Тогда уравнение Шредингера принимает вид:

, (4.3)

то есть гамильтониан системы представляет теперь сумму гамильтонианов отдельных электронов.

Решением (4.3) является функция

. (4.4)

Каждая удовлетворяет одноэлектронному уравнению Шредингера,

в котором взаимодействие i-го электрона с остальными описывается потенциалом .

Таким образом, введение эффективного поля позволяет свести многоэлектронное уравнение к системе одноэлектронных. При этом энергия системы . Функция (4.4) является решением уравнения Шредингера для кристалла, однако не удовлетворяет принципу Паули.

Согласно принципу Паули, в одном квантовом состоянии, характеризуемом волновой функцией , не может находиться более двух электронов с разной ориентацией спинов. Удовлетворяющая этому условию полная волновая функция системы должна быть антисимметричной, то есть менять знак при перемене местами двух электронов. Эту функцию записывают в виде определителя Слэтера:

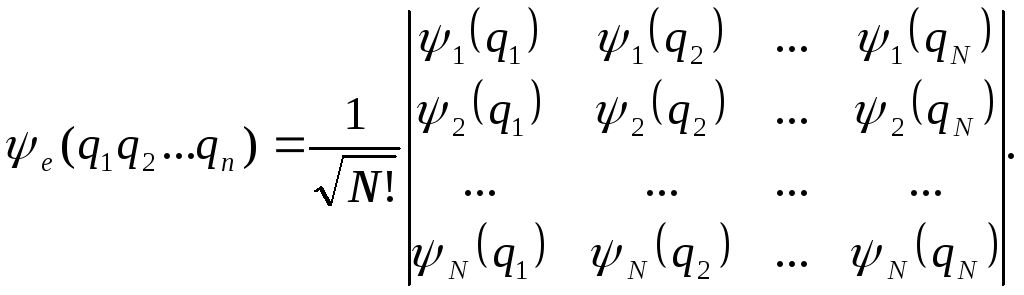
Здесь N-число электронов, q обозначает набор трех пространственных координат и проекций спина, множитель обеспечивает нормировку функции. Антисимметричные свойства вытекают из свойств определителя.

Обозначим потенциальную энергию электрона в кристалле и запишем уравнение Шредингера в виде

.

Атомы в кристалле расположены строго периодически, поэтому полный потенциал кристалла должен обладать трехмерной периодичностью.