Лекция 7

4.Квантовые статистики и их применения

4.1. Квантовые статистики

В квантовой физике, как и в статистической, закономерно­сти имеют вероятностный, статистический характер. Однако есть и принципиальное отличие: в квантовой физике статисти­ческий (вероятностный) подход лежит в самой природе микро­частиц, в их волновых свойствах.

Согласно квантовой теории все микрочастицы подразделяют на два класса, которым соответствуют две квантовые статисти­ки:

1. частицы с полуцелым спином, их называют фермионами; они подчиняются статистике Ферми-Дирака;

2. частицы с целым спином — бозоны; они подчиняются статистике Бозе-Эйнштейна.

Других возможностей квантовая теория не допускает. Нет частиц, подчиняющихся классической статистике Больцмана. Последняя является приближенным предельным случаем, в ко­торый переходят при определенных условиях эти две кванто­вые статистики. Физическая природа различия этих двух квантовых статистик вытекает из принципа неразличимости тождественных частиц, согласно которому суще­ствуют два типа волновых -функций, описывающих состояние тождествен­ных частиц, — симметричные и антисимметричные.

Во всех трех статистиках (классической, Бозе-Эйнштейна и Ферми-Дирака) допустимые микросостояния считаются равно­вероятными. Но различие их — в способах определения мик­росостояний и статистических весов. В статистике Больцмана считается, что даже тождественные частицы принципиально различимы. В квантовых же статистиках, наоборот, считается, что тождественные частицы принципиально неразличимы.

В статистике Ферми-Дирака в каждом квантовом состоянии может находиться не более одной частицы (принцип Паули), а в статистике Бозе-Эйнштейна - любое число частиц.

Различие статистик поясняет табл. 1, где показано как в каждой из них размещаются две тождественные частицы а и b по трем квантовым состояниям (клеткам). Видно, что в статистике Больцмана всех микросостояний де­вять и вероятность каждого из них равна 1/9.В статистиках же Бозе-Эйнштейна и Ферми-Дирака состоя­ния в первых трех парах распределения Больцмана неразличи­мы, и каждая пара рассматривается как одно состояние. Части­цы а и b принципиально неразличимы, поэтому они обозначе­ны просто точками. Для бозонов число микросостояний равно шести, и вероятность каждого из них1/6. Для фермионов по­следние три распределения статистики Бозе-Эйнштейна невоз­можны (принцип Паули). Остается только три микросостоя­ния, и вероятность каждого из них равна 1/3.

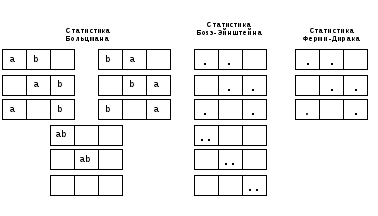
Фазовые ячейки. Основная задача квантовых статистик - это нахождение соответствующих им функций распределения частиц по тем или иным параметрам (например, по энергиям), а также определение средних значений этих параметров, ха­рактеризующих наиболее вероятное макросостояние всей сис­темы частиц.

Для описания состояния системы частиц рассматривают во­ображаемое шестимерное пространство, каждая точка которого характеризуется шестью координатами: х, у, z, р_х, р_y, р_z. Это так называемое фазовое пространство. Состояние системы определяется тем, как распределены в этом пространстве точ­ки, изображающие состояния всех N частиц системы. При этом нужно учесть присущий частицам корпускулярно-волновой ду­ализм, согласно которому неопределенности координаты х и со­ответствующей проекции импульса р_х могут быть определены только с неопределенностью x и р_х, произведение которых, согласно принципу неопределенностей Гейзенберга, xp_x h. Аналогично и для других пар: y и р_у, z и р_z. Поэтому естественно считать, что данному состоянию части­цы в фазовом пространстве соответствует не точка, а фазовая ячейка, объем которой

. (4.1)

Распределение частиц по таким фазовым ячейкам есть пре­дельно подробное квантовое описание состояния системы. Нас будет интересовать наиболее вероятное распределение частиц по фазовым ячейкам. Решение этой задачи достаточно сложно, поэтому мы приведем лишь оконча­тельные результаты - распределения частиц по энергиям

Квантовые распределения. Эти распределения представля­ют собой функции , определяющие средние числа частиц в одной фазовой ячейке с энергией , или функции заполнения ячеек:

для фермионов (4.2)

для бозонов (4.3)

Здесь  - так называемый химический потенциал (некоторая характерная энергия, значение которой можно найти из усло­вия нормировки: суммарное число частиц во всех фазовых ячейках должно быть равно полному числу N частиц макроси­стемы).

Остановимся подробнее на особенностях этих распределе­ний.

1. Для фермионов функция 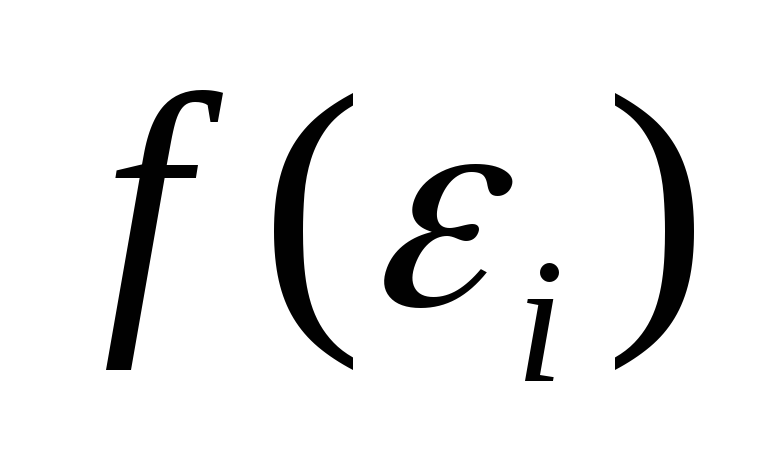не может быть больше еди­ницы, а для бозонов ее значение может быть любым (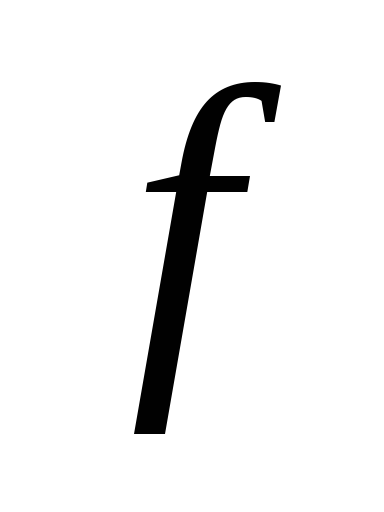 0).

2. Если 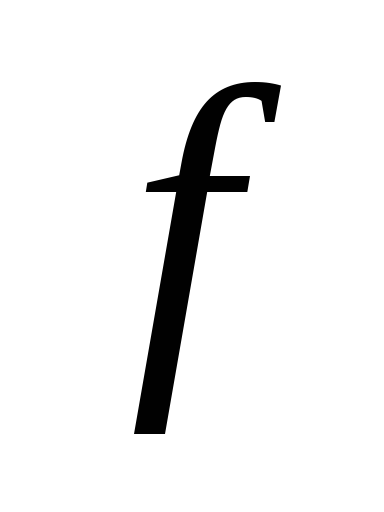<<1, то в знаменателях обоих распределений можно пренебречь единицей, и формула переходит в

, (4.4)

т.е. в распределение Больцмана (А — нормировочный коэффи­циент). Значит, классическое распределение Больцмана спра­ведливо лишь тогда, когда малы «числа заполнения» фазовых ячеек,— при условии <> << 1. Особо отметим, что в этом случае речь идет о совпадении формул, а отнюдь не о том, что изменя­ется поведение частиц (фермионы остаются фермионами, бозо­ны — бозонами).

3. В макросистеме уровни энергии 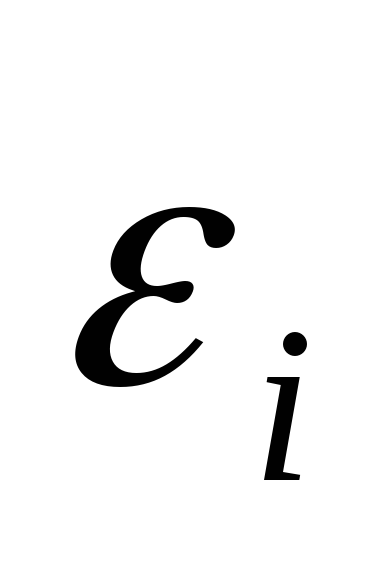частиц квазинепрерыв­ны (расположены очень плотно). Поэтому индекс i у 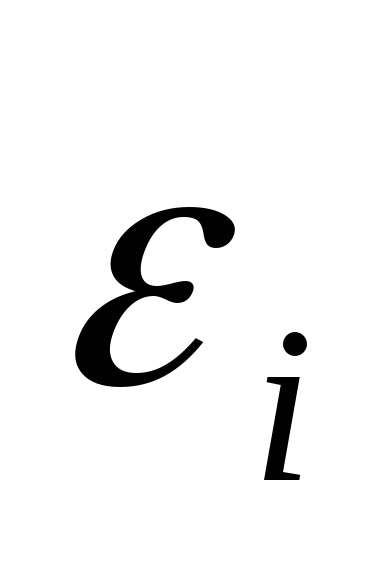можно опустить.

4. Для бозонов значения  в (4.3) не могут быть положитель­ными, иначе при 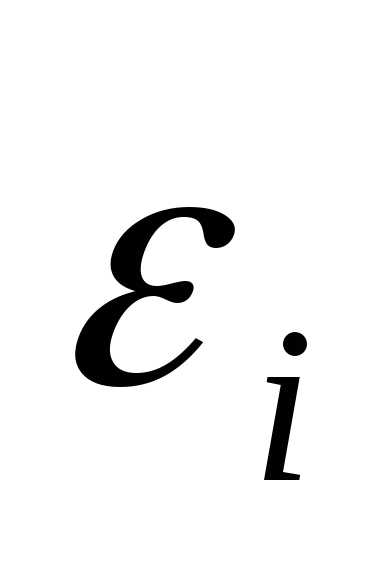<  окажется, что 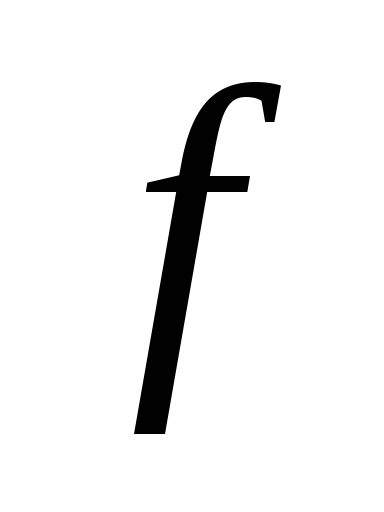< 0, а это лишено физи­ческого смысла. Таким образом, для бозонов  < 0. У макроси­стем с переменным числом бозонов (к числу которых относят­ся, например, фотоны)  = 0, и формула (4.3) переходит в

. (4.5)

Для фермионов подобного ограничения не существует.

Число фазовых ячеек. До сих пор мы имели дело с функ­цией , характеризующей среднее число частиц с энергией  в одной фазовой ячейке. Для дальнейших целей не­обходимо найти число фазовых ячеек, в интервале энергий .

Чтобы определить , найдем сначала соответствующий объем d фазового шестимерного пространства. Для этого в им­пульсной части фазового пространства выделим шаровой слой радиусом, равным импульсу p частицы, и толщиной . Его объем равен . Умножив его на объем координатной части фазового пространства (это объем макросистемы), получим искомый элемент объема фазового пространства:

. (4.6)

Число фазовых ячеек в этом элементе объема получим, разделив на объем одной фазовой ячейки, равный соглас­но (4.1). Кроме того, в дальнейшем нас будет интересовать чис­ло фазовых ячеек, приходящихся на единицу объема обычного пространства, поэтому будем считать, что = 1. Таким обра­зом, число фазовых ячеек в расчете на единицу объема, занима­емого газом, будет равно

. (4.7)

Эта величина имеет размерность м

Переход от импульсов к энергиям зависит от природы час­тиц. Это будет конкретизировано в дальнейшем.

Распределение частиц. Зная число фазовых ячеек в ин­тервале энергий и среднее число частиц в каждой ячейке, т.е. функцию заполнения f, мы можем найти число ча­стиц dn в данном интервале энергий (в расчете на единицу объ­ема газа):

(4.8)

где  — числовой коэффициент порядка единицы, он связан со спецификой частиц идеального газа.