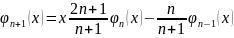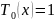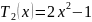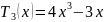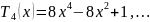infoteh4part
.docxИНФОРМАЦИОННАЯ ТЕХНИКА. ЧАСТЬ 4.
Королев С.А.
каф. 2
Алгоритмы обработки информации
В ИИС реализуется множество алгоритмов обработки информации в соответствии с функциями системы, особенностями контролируемого объекта или процесса, с особенностями структуры системы.
Выделим следующие группы алгоритмов обработки информации:
Алгоритмы, связанные с централизацией выполнения определенных функций (выполнение одним устройством операций с сигналами от разных источников):
алгоритмы дискретизации во времени
алгоритмы массового обслуживания
алгоритмы сжатия информации
Алгоритмы повышения помехоустойчивости или нейтрализации влияния внешних факторов:
алгоритмы фильтрации
алгоритмы коррекции
алгоритмы стат. анализа (определение вероятностных характеристик, корреляционных функций, спектральных плоскостей и т.д.)
Алгоритмы восстановления значений сигналов и аппроксимации:
алгоритм восстановления дискретных сигналов (по отсчетам)
алгоритмы приближения
алгоритм оптимального обнаружения и различения сигналов
алгоритм обработки эмпирических (экспериментальных данных) зависимостей
Варианты задач обработки информации:
на непрерывном или дискретном множестве входных значений
ансамбль входных значений – во времени или в пространстве
в условиях шумов или нет
Нас прежде всего интересует информационный аспект реализации алгоритмов обработки информации (т.е. неоднозначность или погрешность преобразований), а не их техническая реализация.
Алгоритмы восстановления значений сигналов и аппроксимации
Различают следующие классы:
алгоритмы экстраполяции
алгоритмы интерполяции
алгоритмы приближения
Задачи 1. и 2. часто возникают при необходимости восстановления значений сигналов, теряемых вследствие их дискретизации. Использование для этих целей интерполяционных рядов Котельникова для ИИС реального времени неэффективно, но и даже невозмоно.
Экстраполяция
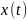 – исходный
сигнал.
– исходный
сигнал.
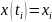 – отсчеты
сигнала
– отсчеты
сигнала
Построение
прогноза значений сигнала
 на
на
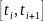 по отсчетам до момента времени
по отсчетам до момента времени
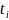 включительно. Простейший случай – по
одному отсчету
включительно. Простейший случай – по
одному отсчету
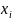 .
В этом случае используют экстраполяцию
нулевого порядка или 0 ступенчатую
экстраполяцию.
.
В этом случае используют экстраполяцию
нулевого порядка или 0 ступенчатую
экстраполяцию.


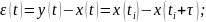
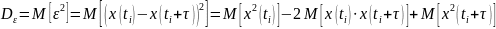
Считая
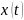 стационарным случайным процессом,
получим:
стационарным случайным процессом,
получим:
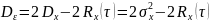
В конце интервала экстраполяции ошибка увеличивается и равна:
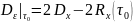
Рассмотрим случай, когда сигнал зашумлен, тогда (считаем шум аддитивным):
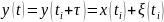
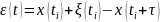
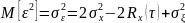
Оценка
средней по интервалу
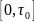 дисперсии ошибки:
дисперсии ошибки:
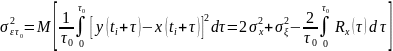
Для оптимизации экстраполяции зашумленного сигнала можно использовать алгоритм статистической экстраполяции по нескольким предыдущим отсчетам (т.е. как линейную функцию взвешенных отсчетов с шумом).
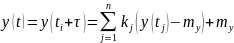
 – неопределенные
коэффициенты, их следует определить из
условия минимизации СКО.
– неопределенные
коэффициенты, их следует определить из
условия минимизации СКО.
Тогда, считая шум центрированным и аддитивным:

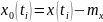
Определение
- из минимизации
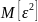 (по сути, это алгоритм оптимальной
фильтрации), т.е. из системы уравнений:
(по сути, это алгоритм оптимальной
фильтрации), т.е. из системы уравнений:
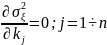
Оптимизация
по одному отсчету (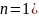 дает результат:
дает результат:

Следовательно,
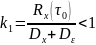
Видно,
что экстраполированное значение всегда
ближе к среднему значению
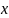 .
.
Линейная экстраполяция по двум точкам

Рассмотрим задачу с шумом:
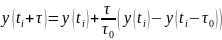

В конце интервала экстраполяции:
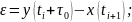
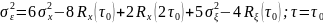
Т.к.
при
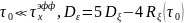
Если
при этом
 ,
то
,
то
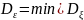
Считаем,
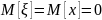
Алгоритм интерполяции
Возможна
задача интерполяции по всем отсчетам
(массив отсчетов есть). Имеем отсчеты
сигнала
 .
Оценка (восстановление) значений сигнала
на интервале
.
Оценка (восстановление) значений сигнала
на интервале
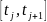 осуществляется в общем случае по
значениям всех отсчетов
,
причем в точках отсчетов
осуществляется в общем случае по
значениям всех отсчетов
,
причем в точках отсчетов
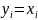 .
.
Применение алгоритмов интерполяции:
в ИИС реального времени – восстановление значений в по значениям отсчетов
 – используется запаздывание на шаг.
– используется запаздывание на шаг.в системах идентификации пространств распределенных объектов или полей, например:
поле энерговыделения
таблицы параметров воды/пара
Простейшие алгоритмы интерполяций для ИИС
- линейная интерполяция


Ошибка восстановления значений сигнала:
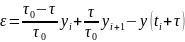
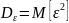
Для середины интервала интерполяции:
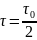
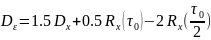
Если
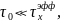 то
то
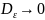
Алгоритмы интерполяции, требующие использования вычислительных средств.
Сплайн-интерполяция
Сплайн
представляет собой функции, склеенные
из различных кусков многочленов по
заданному базису. Если в качестве
базисных функций выбрать функции вида:
1,
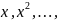 то сплайны полиномиальные.
то сплайны полиномиальные.
Преимущества: простота реализации и устойчивость к локальным возмущениям.
Функцию
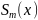 называют полиномиальным сплайном
дефекта
называют полиномиальным сплайном
дефекта
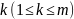 ,
если на отрезках между соседними узлами
она принадлежит множеству полиномов
степени не выше
,
если на отрезках между соседними узлами
она принадлежит множеству полиномов
степени не выше
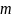 и имеет на заданной области изменения
и имеет на заданной области изменения
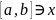 непрерывные производные порядка, не
ниже
непрерывные производные порядка, не
ниже
 .
.
Обычно
используют сплайны с
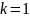 .
Для задач интерполяции удобно использовать
сплайны нечетных степеней. Сплайн первой
степени реализует кусочно-линейную
интерполяцию. Кубический сплайн при
обеспечивает непрерывность второй
производной на отрезке
.
Для задач интерполяции удобно использовать
сплайны нечетных степеней. Сплайн первой
степени реализует кусочно-линейную
интерполяцию. Кубический сплайн при
обеспечивает непрерывность второй
производной на отрезке
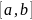 и находится решением системы линейных
алгебраических уравнений.
и находится решением системы линейных
алгебраических уравнений.
Задана сетка (равномерная) на отрезке .
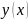 – исходная
интерполируемая функция на сетке
– исходная
интерполируемая функция на сетке

Обозначим
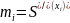 - вторая производная в точке
.
Она линейна на
- вторая производная в точке
.
Она линейна на
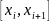 ,
тогда:
,
тогда:
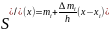
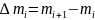

Далее:
интегрируем это выражение дважды на отрезке ;
то же самое выполним на отрезке
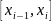 ;
;учтем требование для кубического сплайна:
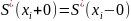 .
.
После двукратного интегрирования на отрезке получаем:
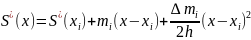
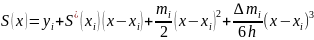
Полагая
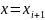 ,
находим
,
находим
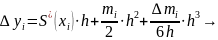
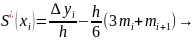

Следовательно,
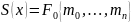 на отрезке
с учетом граничных условий. Получаем
систему
на отрезке
с учетом граничных условий. Получаем
систему
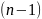 алгебраических уравнений относительно
неизвестных
алгебраических уравнений относительно
неизвестных
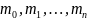 .
.
Рассмотрим
функцию
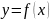 .
Введем определения:
.
Введем определения:
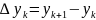 -
первая
нисходящая разность
-
первая
нисходящая разность
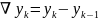 -
первая
восходящая разность
-
первая
восходящая разность
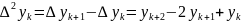 – вторая
разность
(порядка два)
– вторая
разность
(порядка два)
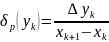 – первая
разделенная разность
– первая
разделенная разность
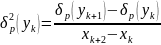 -
вторая
разделенная разность
-
вторая
разделенная разность
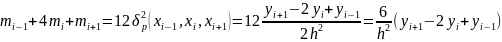
где
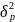 – вторая разделенная разность функции
– вторая разделенная разность функции
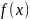 на точках
на точках
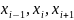 .
.
Целесообразность использования сплайнов
При наличии большого количества точек-отсчетов при построении единого интерполирующего полинома потребуется использовать полиномы/многочлены больших степеней, что очень неудобно для вычислений, а также приводит к большой чувствительности решения к возмущениям.
Сплайн
аппроксимация позволяет использовать
много полиномов с небольшими степенями,
обычно
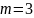 или
или
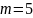 .
.
Другие алгоритмы интерполяции (по формулам Лагранжа, Ньютона, Бесселя и т.д.) используются редко и только в системах обработки информации в объемах с распределенными параметрами.
Алгоритмы аппроксимации на принципах приближения
Применение:
Аналитическая градуировка датчиков;
Идентификация характеристик сигналов/ объектов управления/ контроля/ ИС;
Выявление эмпирических зависимостей;
Оценка значений параметров по косвенным измерениям.
Предметом аппроксимации могут быть как непрерывные сигналы или характеристики, так и дискретные наборы данных или отсчетов.
Особые классы задач связаны с аппроксимацией зашумленных данных.
Аппроксимирующие функции
Чаще всего в качестве аппроксимирующих функций используют либо степенные полиномы, либо полиномы, состоящие из ортогональных функций. Использование степенных полиномов:
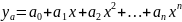
Для
идентификации коэффициентов полинома
степени
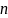 необходимо знать значения в
необходимо знать значения в
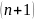 точке. Если число точек (т.е. значений
)
совпадает со степенью полинома
точке. Если число точек (т.е. значений
)
совпадает со степенью полинома
 ,
то задача – однозначная, и по сути
получаем интерполирующий полином. Если
степень меньше, то коэффициенты необходимо
определять исходя из минимизации ошибки
аппроксимации.
,
то задача – однозначная, и по сути
получаем интерполирующий полином. Если
степень меньше, то коэффициенты необходимо
определять исходя из минимизации ошибки
аппроксимации.
Т.е. система уравнений должна быть:
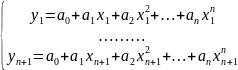
Решение
относительно
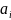 дает возможность определить аппроксимирующую
функцию. Особенностью аппроксимации
степенными полиномами является
зависимость
дает возможность определить аппроксимирующую
функцию. Особенностью аппроксимации
степенными полиномами является
зависимость
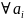 от всех значений функции и точек
,
поэтому при изменении набора данных
приходится все пересчитывать.
от всех значений функции и точек
,
поэтому при изменении набора данных
приходится все пересчитывать.
Аппроксимация полиномами, состоящими из ортогональных функций
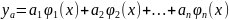
где
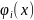 – ортогональные функции. Для них при
– ортогональные функции. Для них при
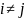 :
:

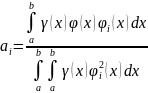
где
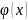 - аппроксимируемая функция. Коэффициент
зависит только от функции
- аппроксимируемая функция. Коэффициент
зависит только от функции
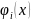 и может быть найден независимо от других
коэффициентов.
и может быть найден независимо от других
коэффициентов.
Критерии точности аппроксимации
Среднеквадратичный критерий:
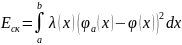
Равномерный критерий:
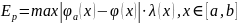
Оценки на дискретных множествах:
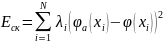
При аппроксимации ортогональными полиномами коэффициенты будут оптимальны с точки зрения минимума квадратичного критерия. В качестве аппроксимирующих многочленов, состоящих из ортогональных функций, могут быть использованы ряды Фурье, классические ортогональные многочлены, многочлены, построенные на функциях Уолсиа и другие.
Классические ортогональные многочлены
Классические ортогональные многочлены – это многочлены Чебышева, Эрмита, Лежандра, Лагерра и т.д.
Ортогональные полиномы Лежандра
|
ортогональны
на отрезке
|
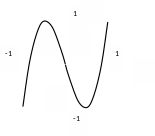
Ортогональные полиномы Чебышева первого рода

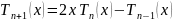
Ортогональность
на
с
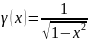
|
Все
экстремумы равны
|
Ортонормированные многочлены Чебышева

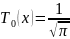
Многочлены Чебышева с единичным старшим коэффициентом
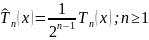
Нули многочленов Чебышева первого рода:
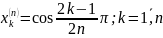
Экстремумы многочленов Чебышева первого рода:
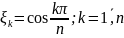
Смещенные многочлены Чебышева
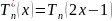
на
отрезке
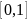 - те же свойства.
- те же свойства.
Многочлены Чебышева второго рода
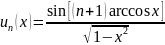
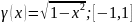
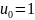
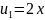

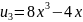
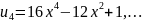
С единичным старшим коэффициентом:
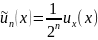
Равномерные приближения
Аппроксимирующие полиномы, рассчитанные по МНК (отрезки рядов Фурье для ортогональных многочленов) в отдельных точках или областях могут давать ошибки, превышающие доступные. Аппроксимация по МНК применима для обработки результатов наблюдения, т.к. позволяет сглаживать локальные ошибки или шумы в отсчетах (например, аналитическая градуировка датчиков).
Однако в ряде задач ИИС необходимо гарантировать, чтобы ошибка не превышала ошибки от заданной величины, т.е. по норме:

где
аппроксимирующая функция
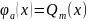 – полином степени
– полином степени
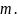
Если
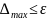 ,
то говорят, что полином
,
то говорят, что полином
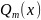 равномерно приближает
на отрезке
с точностью
равномерно приближает
на отрезке
с точностью
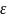 .
.
Если
степень
задана, то ставится задача выбора
коэффициентов полинома
так, чтобы
 ,
т.е.
,
т.е.
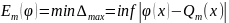 ,
где
,
где
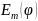 – наименьшее отклонение функции, а сам
полином при этом – полином наилучшего
равномерного приближения – ПНРП.
– наименьшее отклонение функции, а сам
полином при этом – полином наилучшего
равномерного приближения – ПНРП.
Теорема Чебышева:
Для того, чтобы полином
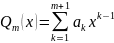
был
ПНРП
на отрезке
,
необходимо и достаточно, чтобы на отрезке
нашлись (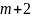 )
точки, в которых разность
)
точки, в которых разность
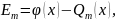
последовательно
чередуясь, принимает свои максимальные
и минимальные значения, по модулю равные
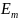 .
Такая система точек называется Чебышевский
альтернанс.
.
Такая система точек называется Чебышевский
альтернанс.

Если
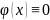 на отрезке
,
то полином, дающий минимум величине
на отрезке
,
то полином, дающий минимум величине
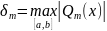
есть полином, наименее уклоняющийся от нуля, или является полиномом Чебышева первого рода.
Теорема: Полином Чебышева степени с единичным старшим коэффициентом наименее отклоняется от нуля на отрезке по сравнению с другими полиномами того же класса, т.е.:
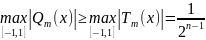
Пример:
для функции
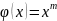 полиномом НРП степени
полиномом НРП степени
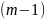
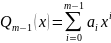
на отрезке является полином:

Отрезок , замена переменной
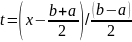
Старший
коэффициент при
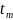 будет равен
будет равен
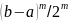 ,
т.е.
,
т.е.
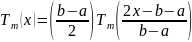
Тогда:
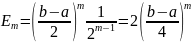
Пример:
равномерно приблизить на отрезке
с помощью полинома первого порядка
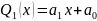 функцию
функцию
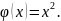
Решение: смещенный полином Чебышева первого рода второго порядка наименее уклоняется от нуля на отрезке . Следовательно,
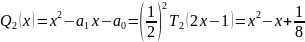
Т.е.:
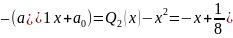
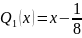
Причем максимальное отклонение при этом:
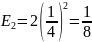
И
достигается в трех точках (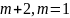 ):
):
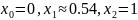 ,
чередуясь
,
чередуясь
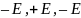 .
.
Вариант методики построения ПНРП
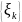 -
Чебышевский
альтернанс
-
Чебышевский
альтернанс

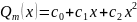
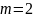 ;
число точек альтернанса равно
;
число точек альтернанса равно
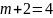
Возьмем
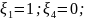
Неизвестные:

Имеем систему:
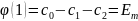
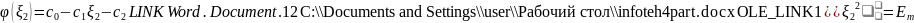


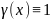
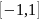
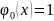
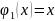
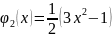
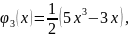 и
т.д.
и
т.д.