книги / Теория линейных электрических цепей. Ч. 2

Таким образом, величина

2	F(k )e j k j	2	F(k )e j k j	2	F( jk )	(1.10)
T	1	T	1	T	1

представляет собой комплексную величину k-й гармоники:

A	A e j k ,	(1.11)
k	k

где Ak T2 F(k 1 ) .

Совокупность амплитуд всех гармоник данной функции может рассматриваться как дискретный спектр этой функции, который показывает зависимость амплитуд гармоник и их начальных фаз от номера гармоники. Его можно представить на графике в виде отрезков вертикальных линий, пропорциональных значениям амплитуд, аналогично для значений начальных фаз каждой гармоники. По оси абсцисс откладываем значения, равные частотам гармоник. Для каждой частоты гармоник откладываем от оси абсцисс параллельно оси ординат отрезки, длины которых равны амплитудам Akm или начальным фазам k гармоник. При этом Akm > 0, а k может быть как положительным, так и отрицательным. Такие характеристики носят название дискретных спектров

или дискретных частотных характеристик – соответственно ампли-тудно-частотной и фазочастотной.

При построении спектра периодического сигнала по оси абсцисс откладывают кратные основной частоте значения частот гармонических составляющих. Обратим внимание на то, что чем больше период функции f(t), тем плотнее расположены спектральные линии и соответственно меньше значения амплитуд гармонических составляющих. Разумеется, в конкретных случаях те или иные частотные составляющие спектра сигнала могут отсутствовать, но составляющих, частота которых не кратна основной частоте, спектр содержать не может.

Пример. Определим спектр периодической последовательности прямоугольных импульсов амплитуды F0 с длительностью,

11

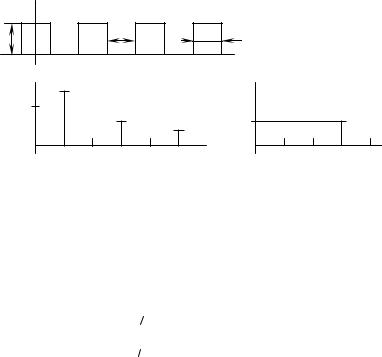
равной половине периода, T/2 (рис. 1.3, а). Аналитическое выражение временной зависимости рассматриваемого сигнала в этот период имеет вид

F f (t) 0

0

	при	0 t T				,
		T		2
	при		t	3	T.
		2		2

	F0	T	T
				t
	Akm	а
				k
	F0
		3 1	k 1	k 1
	1			3 1
			5 1
		б		в
			Рис. 1.3

Если за начало отсчета выбрать начало координат, то функция будет обладать четной симметрией и содержать только косинусные составляющие с коэффициентами Akm. Определим амплитуду k-й гармоники:

		2	T 4		2F		k
	Akm			F0 cos k 1tdt	0	sin		.
		T			k		2
			T 4

Отсюда:

A

2F0

; A

1

2F0

; A

1

2F0

;

A F ;

1m

3m

3

5m

5

0 0

A2m A4m 0;

Bkm 0.

12

Найденные коэффициенты позволяют записать разложение Фурье:

f (t)	F0		2F0	(cos t	1 cos3 t		1 cos5 t ).
2				1	3	1	5	1

Коэффициенты ряда принимают следующие значения:

A		F0	;	A	2F0	(k 1, 2, 3 );
0	2			km	k

k 0 (k 4n 1, n 0,1, 2, );

k (k 4n 1, n 1, 2, 3, ).

Спектры амплитуд и фаз рассматриваемой функции показаны на рис. 1.3, би в.

1.1. Максимальное, среднее и действующее значения несинусоидальной функции

Максимальное значение несинусоидальной периодической функции – наибольшее по модулю значение функции за период.

Среднее значение за период определяется по формуле

Fср 1 T f (t)dt .

T 0

Для синусоиды и всех симметричных относительно оси абсцисс сигналов эта величина равна нулю. Поэтому для кривых, симметричныхотносительнооси абсцисс, среднеепомодулю значение

	T	0
F	1	T	f (t)	dt .	(1.12)
ср

Это значение зависит от начальных фаз k. Если за начало отсчета принять момент прохождения через нуль первой гармоники функции, то для кривых, не содержащих постоянную составляющую, после интегрирования получим:

13

4

1

F

F

F

cos

k

.

k

ср

T

1m

k

mk

1

k 3,5,7

Если кривая f(t) симметрична относительно оси абсцисс и в течение половины периода ни разу не изменила знака, то среднее по модулю значениеравно среднему значению заполовину периода:

Fср 2 T2 f (t)dt , T 0

причем начало отсчета времени в этом выражении должно быть выбрано так, чтобы f(0) = 0. Если за весь период функция ни разу не изменила знака, то среднее по модулю значение равно постоянной составляющей.

При несинусоидальных периодических воздействиях, как и при синусоидальных, обычно под значением ЭДС, тока или напряжения понимают действующее значение.

Действующее значение несинусоидальной функции – это среднеквадратическое значение за период мгновенного значения функции:

	F	1	T	f 2 (t)dt .	(1.13)
		T
			0

Определим действующее значение на примере напряжения. Пусть

u(t) U0 U1m sin 1t 1 U2m sin 2 1t 2 ,

тогда

u2 (t) U0 U1m sin 1t 1 U2m sin 2 1t 2 2

U02 Ukm2		sin2 k 1t k U0 Ukm sin k 1t k (1.14)
	k 1	k 1
	U pmUqm sin p 1t p sin q 1t q .

p 1, q 1, p q

14

Рассмотриминтегралыоткаждогоиз слагаемыхв отдельности:

	T	0
1.	1	T U02dt U02			– это			квадрат постоянной составляющей
напряжения.
2.	1	T U	2	sin2 k t			dt Ukm2		U 2	, так как этот интеграл
			km			k
	T 0				1			2	k

по определению равен квадрату действующего значения Uk гармонической составляющей напряжения k-й гармоники.

3. 1 T U0Ukm sin k 1t k dt 0 , так как интеграл от синусои-

T 0

дальной величины за целое число периодов равен нулю.

	4.	1	T U pmUqm sin p 1t p sin q 1t q dt	1	T	U pmUqm
		T		T		2
			0		0

[cos( p 1t p q 1t q ) cos p 1t p q 1t q ]dt 0 ,

где p q; подынтегральное выражение является разностью двух косинусоидальных функций, интеграл каждой из которых за целое число периодов равен нулю.

Таким образом, действующее значение периодического несинусоидального напряжения

	U	U02	U 2		U 2		U02 U12 U22 , (1.15)
			1m		2m
			2		2

т.е. действующее значение периодического несинусоидального напряжения равно корню квадратному из суммы квадратов постоянной составляющей и квадратов действующих значений всех гармонических составляющих. Так же определяется дейст-

вующее значение периодического несинусоидального тока:

	I	I02	I 2		I 2		I02 I12 I22 .
			1m		2m			(1.16)
			2		2

15

Аналогичным образом определяется действующее значение любой другой периодической несинусоидальной величины.

Несинусоидальные токи и напряжения измеряют приборами различных систем. Приборы электромагнитной, электродинамической и тепловой систем реагируют на действующее значение, магнитоэлектрические приборы с выпрямителем – на среднее значение, магнитоэлектрические без выпрямителя – на постоянную составляющую.

1.2. Коэффициенты, характеризующие периодические несинусоидальные функции

В электротехнике при оценке несинусоидальных периодических кривых пользуются коэффициентом формы кривой kф, ко-

эффициентом амплитуды kа и коэффициентом искажения kи.

Коэффициент формы определяется как отношение действующего значения функции к среднему значению функции, взятой по модулю:

1

T

f 2 (t)dt

k

F

T

0

.

(1.17)

ф

Fср

1

T

f (t)

dt

T

0

Коэффициент амплитуды определяется как отношение максимального значения функции к ее действующему значению:

	kа			Fm					Fm		.	(1.18)
				F				T
					1
								f 2 (t)dt
							T
								0
Для синусоиды kф				1,11; kа						2 1,41.
	2	2
16

Коэффициент искажения определяется как отношение действующего значения основной (первой) гармоники к действующему значению всей функции:

kи				F1	.	(1.19)
			T
1				f 2 (t)dt
		T
			0

Для синусоиды kи 1.

В электронике и радиотехнике для оценки искажений пользуются коэффициентом гармоник, определяемым как отношение действующего значения высших гармоник к действующему значению основной гармоники:

		1
	kг		Fk2 .	(1.20)
		F1
			k 2

Коэффициенты kа, kф характеризуют форму периодических кривых, т. е. их отличие от синусоиды, и используются в силовой электротехнике, радиотехнике и т. д. Коэффициенты kг и kи являются показателями качества электрической энергии энергосистем. В энергетической электронике при оценке результатов преобразования переменного синусоидального тока в постоянный используются коэффициент среднего значения kср (отношение среднего значения к амплитудному, для синусоиды kср = 0) и коэффициент пульсаций kп (отношение амплитуды основной гармоники к постоянной составляющей).

1.3.Активная и полная мощность несинусоидального тока

Выражение мгновенной мощности

p(t) u(t)i(t)

(1.21)

справедливо для токов и напряжений с любой формой кривой.

17

Под активной мощностью несинусоидального тока понимают, как и в цепях синусоидального тока, среднее значение мгновенной мощности за период первой гармоники:

	P	1	T uidt .	(1.22)
		T
			0

Если представить напряжения и ток рядами Фурье:

u U0	U1m sin 1t u1 U2m sin 2 1t u2	,
i I0	I1m sin 1t i1 I2m sin 2 1t i2	,

то активная мощность будет представлена суммой интегралов тех же четырех типов, что и при рассмотрении действующего значения периодического несинусоидального тока.

Таким образом,

P P0 P1 Pk

,

(1.23)

U

I

0

U

I

cos U

I

k

cos

k

0

1

1

1

k

где k uk ik .

Активная мощность при периодических несинусоидальных токах и напряжениях равна сумме активных мощностей постоянной (мощности постоянного тока) и всех гармонических составляющих тока и напряжения.

Реактивной мощностью периодических несинусоидальных токов можно условно считать величину, равную сумме реактивных мощностей отдельных гармоник:

Q Q1 Q2 U1I1 sin 1 U2 I2 sin 2 .

(1.24)

По аналогии с синусоидальными токами вводят понятие полной мощности, определяемой как произведение действующих значений токов и напряжений:

S UI

U02 U12 U22

I02 I12 I22 . (1.25)

18

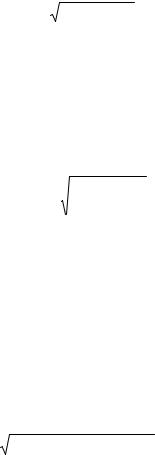
В отличие от цепи синусоидального тока,

S 2 P2 Q2 ,

S 2 P2 Q2

(равенство имеет место при активной нагрузке). Это объясняется тем, что полная мощность содержит все гармоники, в том числе и произведения токов и напряжений разной частоты, поэтому для несинусоидальных токов квадрат полной мощности обычно больше суммы квадратов активной и реактивной мощностей.

Мощность искажения

T

S 2 P2 Q2

(1.26)

характеризует степень различия в формах кривых напряжения u и тока i.

По аналогии с синусоидальными функциями отношение активной мощности при несинусоидальных токах к полной мощно-

сти условно называют коэффициентом мощности ,

		P			Pk	,	(1.27)
					k 0
		S		Uk2 Ik2
				k 0	k 0

это косинус угла сдвига фаз между эквивалентными синусоидами напряжения и тока, которые имеют те же действующие значения, что и несинусоидальные напряжения и ток, а потребляемая цепью мощность остается такой же, как при действительном несинусоидальном режиме. Коэффициент 1, если цепь обладает только однимактивным сопротивлением, во всехостальных случаях 1.

Пусть напряжение синусоидально, а ток несинусоидален. В этом случае

P U1I1 cos 1 UI1 cos 1 .

Действующее значение тока

I I02 I12 I22 Ik2 I1 .

19

Следовательно,
UI1 cos 1		I1	cos k	и	cos ,	(k	и	1).
UI		I	1		1

Таким образом, появление высших гармоник в кривых напряжения и тока приводит к снижению коэффициента мощности по сравнению со случаем, когда ток и напряжение при тех же действующих значениях синусоидальны. Следовательно, хотя бы в этом отношении появление высших гармоник нежелательно. Поэтому стремятся конструировать генераторы переменного тока так, чтобы кривая ЭДС в них была по возможности близка к синусоиде. Наличие высших гармоник может быть причиной и ряда других нежелательных явлений. Оно приводит к возможности резонанса для одной из высших гармоник и, соответственно, к появлению перенапряжений на отдельных участках цепи, к нежелательному влиянию гармоник звуковой частоты на радио- и телефонную связь. Однако в ряде специальных радиотехнических, электроизмерительных и различных электронных устройств оказывается необходимым как раз получить формы кривых напряжения и тока, отличающиеся от синусоидальных, т.е. содержащиевысшиегармоники.

Поскольку идеальных синусоидальных величин практически не бывает, то в технике существует понятие практически синусоидальных кривых. Форма кривой считается практически синусоидальной, если все ее ординаты отличаются от ординат первой гармоники не более чем на 5 %. При этом количество контрольных точек должно быть не менее 12.

1.4. Расчет линейной электрической цепи при несинусоидальных периодических воздействиях

Если в линейной электрической цепи действует один или несколько источников несинусоидальных периодических ЭДС и токов, торасчет такойцепиведется втриэтапа.

1. Разложение ЭДС и токов источников на постоянную и синусоидальные составляющие, т.е. в ряд Фурье. Часто встречающиеся

20