книги / Сопротивление материалов. Ч. 1

Например, для стали E = 2 105 МПа, µ = 0,25, откуда следует, что G = 0,8 105 МПа. Зависимость (5.7) подтверждается экспериментально.

Напряжение τт является пределом текучести при сдвиге, т.е. ка-

сательным напряжением, при котором угол сдвига возрастает при постоянном напряжении. Характерно, что для многих материалов предел текучести при сдвиге τт связан с пределом текучести при растяжении σт соотношением

τT ≈ σT3 .

Запишем выражение для абсолютного сдвига ∆, подставив в формулу закона Гука (5.6) полученные ранее соотношения (5.2) и (5.5):

	τ=Gγ,
или
	Q	=G		∆		,
	A			a
откуда
	∆=		Qa			,	(5.8)
			GA

где произведение GA называют жесткостью сечения стержня при сдвиге.

Практические расчеты соединений, работающих на сдвиг

Детали, служащие для соединений отдельных элементов машин и строительных конструкций, – заклёпки, штифты, болты и т.п. – во многих случаях воспринимают нагрузки, перпендикулярные к их продольной оси. Поперечная нагрузка в указанных деталях возникает, в частности, при растяжении (сжатии) соединяемых элементов. Соответствующие примеры приведены на рис. 5.7, где изображены: а – штифт; б – заклёпка; в – болт, поставленный без зазора; г –

71

шпонка. Их действительная работа сложна и лишь приближенно может быть охарактеризована как работа на сдвиг (срез). Однако практические расчёты этих соединений очень просты и достаточно надёжны, так как расчётные сопротивления назначаются на основании опытных данных.

а

б

в

г

Рис. 5.7.

Расчеты деталей на срез базируются на следующих основных допущениях:

1)в поперечном сечении возникает только один внутренний силовой фактор – поперечная сила Q;

2)касательные напряжения распределены равномерно по площади поперечного сечения;

3)в случае, если соединение осуществлено несколькими одинаковыми деталями (заклепками и т.п.), принимается, что все они нагружены одинаково.

Разрушение соединительных элементов (в случае недостаточной прочности) происходит в результате их перерезывания по плоскости, совпадающей с поверхностью соприкосновения соединяемых деталей, как показано на рис. 5.8, поэтому говорят, что эти элементы работают на срез, и возникающие в их поперечном сечении касательные напряжения называют напряжениями среза и обозначают τср.

72

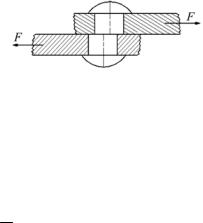
Рис. 5.8.

Условие прочности на срез формулируется как

τ	ср	=	Q	≤R	,	(5.9)
				ср
			Aср

где Q – поперечная сила; при нескольких одинаковых соединитель-

ных деталях, Q = Fп ; здесь F – общая нагрузка соединения, п – чис-

ло заклёпок (болтов и т.п.); Rср – расчётное сопротивление на срез материала соединительных элементов.

Формула (5.9) используется для проверочного расчёта соединения. В зависимости от постановки задачи она может быть преобразована для определения допускаемой (расчётной) нагрузки или требуемой площади сечения.

Расчёт на срез обеспечивает прочность соединительных элементов, но не гарантирует надёжность соединения в целом. При недостаточной толщине соединяемых элементов возможно нарушение соединения вследствие их смятия по поверхности контакта с соединительными деталями. Давления, возникающие между поверхностями отверстий и соединительных деталей, принято называть напряжениями смятия и обозначать σсм. Фактическое распределение контактных напряжений весьма сложно. Поэтому расчёт на смятие носит условный характер и ведётся в предположении, что силы взаимодействия между деталями равномерно распределены по поверхности контакта и нормальны к этой поверхности.

Условие прочности на смятие имеет вид

σ		=	F	≤R	,	(5.10)
			пA
	см			см
			см
						73

– нагрузка на одну соединительную деталь; Aсм – расчётная

где Fп

площадь смятия; Rсм – расчётное сопротивление на смятие, определяемое экспериментально.

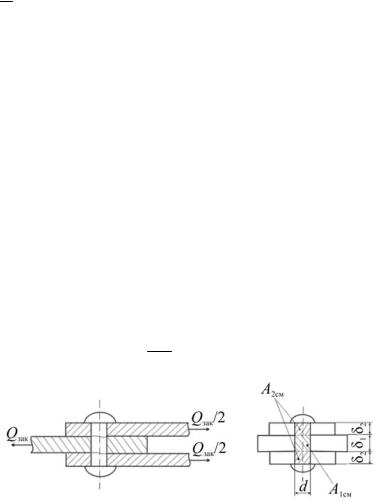
За расчётную площадь смятия при контакте по плоскости (см. рис. 5.7, г) принимают действительную площадь соприкосновения Aсм = tl, где l – размер шпонки в направлении, перпендикулярном плоскости чертежа; при контакте по цилиндрической поверхности (см. рис. 5.7, а, б, в) принимают площадь проекции поверхности контакта на диаметральную плоскость, т.е. Aсм = δd. При различной толщине соединяемых элементов в расчётную формулу следует подставлять δmin .

Для примера рассмотрим некоторые вопросы расчета заклёпочных соединений для случаев, когда соединяемые элементы работают на растяжение и сжатие.

На рис. 5.9, а показана работа одиночной заклёпки, соединяющей три листа и называемой двухсрезной, так как при её разрушении срез происходит по двум сечениям (отмечено волнистой лини-

ей) с площадью среза Aср = πd4 2 .

а

б

Рис. 5.9.

Зависимости для проверочных расчётов имеют следующий вид:

а) на срез

74

τ	ср	=				F		≤R ,		(5.11)
						πd 2
				nk					ср
						4
где п – общее число заклёпок, передающих заданную нагрузку F;
k – число плоскостей среза одной заклёпки;
d – диаметр заклёпки;
б) на смятие
	σ		=			F	≤R		,	(5.12)
					ndδ
		см						см

где δ – наименьшая суммарная толщина листов, сминаемых в одном направлении. Например, на рис. 5.9, б это будет меньшая из площадей A1см = = δ1 d и A2см = 2 δ2d.

Допускаемую силу на одну заклёпку определяют следующим образом:

а) из условия прочности на срез

Q	зак	=R k		πd	2	;	(5.13)
ср			ср	4
б) из условия прочности на смятие
Qзак =R dδ					.		(5.14)
	см		см

Из двух сил фактической допускаемой силой для заклёпки Qзак является меньшая из них.

Расчёт заклёпочного соединения обычно состоит в определении необходимого числа заклёпок п при действии на него заданной нагрузки F. Тогда

п=	F	.	(5.15)
	Q
	зак

75

Лекция 6

КРУЧЕНИЕ

Основные понятия. Крутящие моменты и их эпюры

Кручение – это такой вид нагружения стержня, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент, обозначаемый Mк (или Мz). Стержень, работающий на кручение, называют валом.

Деформация кручения возникает при нагружении стержня парами сил, плоскости действия которых перпендикулярны к его продольной оси. Моменты этих пар будем называть скручивающими и обозначать буквой М.

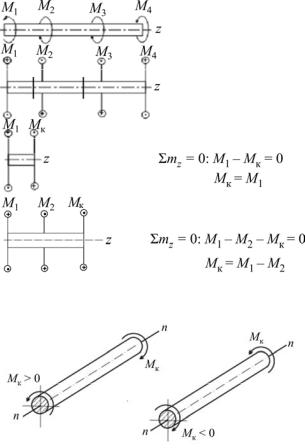
На рис. 6.1, а представлен вал, работающий на кручение под действием приложенных к нему скручивающих моментов. При этом на рис. 6.1, б внешний момент условно изображён в виде двух кружков: кружок с точкой обозначает силу, направленную на наблюдателя, а кружок с крестом – силу, направленную от наблюдателя.

Во всех случаях будем считать, что алгебраическая сумма скручивающих моментов равна нулю, т.е. вал находится в равновесии.

Условимся о следующем правиле знаков: крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали п он направлен против хода часовой стрелки (рис. 6.2). Соответствующий внешний скручивающий момент направлен по ходу часовой стрелки.

76

а

б

в

г

Рис. 6.1.

Рис. 6.2.

Применяя метод сечений и рассматривая равновесие отсечённой части (рис. 6.1, в, г), приходим к выводу, что крутящий момент в поперечном сечении вала численно равен алгебраической сумме скручивающих моментов, приложенных к отсечённой части:

Μк = ∑Μiz .

(6.1)

отс.ч

77

Помимо сосредоточенных скручивающих моментов на вал может действовать и распределённая по некоторому закону моментная нагрузка интенсивностью m(z).

а

б

Рис. 6.3.

Установим дифференциальную зависимость между интенсивностью m и крутящим моментом Мк. Для этого рассмотрим стержень с моментной нагрузкой m (рис. 6.3, а), из которого вырежем элемент длиной dz (рис. 6.3, б)

На него будут действовать моментная нагрузка m = const, которую можно считать равномерно распределённой ввиду малости dz, и уравновешивающие положительные крутящие моменты (в левом сечении – Мк, в правом – Мк+dМк, где dМк – приращение крутящего момента). Составим уравнение равновесия для элемента:

Σmz =0 ; Μк +mdz−(Mк +dMк )=0,

откуда

dMк	=m.	(6.2)
dz

График, показывающий закон изменения крутящих моментов по длине вала, называется эпюрой крутящих моментов. Положительные значения на эпюре будем откладывать вверх от горизонтальной базисной линии, а отрицательные значения – вниз. По-

78

строение эпюры крутящих моментов принципиально ничем не отличается от построения эпюры продольных сил.

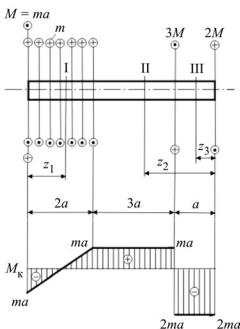
Пример. Построить эпюру крутящих моментов для вала, изображённого на рис. 6.4, а.

а

б

Рис. 6.4.

Решение. Разбиваем вал на три участка: I, II, III. Используя метод сечений, на участке I мысленно проводим в произвольном месте сечение, отбрасываем правую часть вала и рассматриваем равновесие отсечённой левой части с приложенным в месте сечения положительным крутящим моментом Мк и внешней нагрузкой. Тогда

всоответствие с принятым правилом знаков для участка I получаем: I. 0≤z1 ≤2a ;

79

Mк =−ma+mz1;

Mк (0)=−ma;

Mк (2а)=ma.

Проведя произвольные сечения на остальных участках вала, получим соответственно:

II. a≤z2 ≤4a (отбрасываем левую часть);

Mк =−2ma+3ma =ma.

III. 0≤z3 ≤a (отбрасываем левую часть);

Mк =−2ma.

По полученным данным строим эпюру Мк (рис. 6.4, б). На участке I величина крутящего момента линейно зависит от координаты сечения, так как действует равномерно распределённая моментная нагрузка интенсивностью m. На участках I и II крутящий момент не зависит от координаты z, поэтому эпюра имеет вид прямоугольников. В тех сечениях, где приложены внешние сосредоточенные моменты, получаются скачки на величину этих моментов.

Напряжения и деформации при кручении вала круглого поперечного сечения

Теория кручения вала круглого сплошного или кольцевого поперечного сечения основана на следующих допущениях, подтверждаемых экспериментально:

1.Сечения, плоские и нормальные к оси вала до деформации, остаются плоскими и нормальными к его оси и после деформации (гипотеза плоских сечений).

2.Радиусы, проведённые в сечении, остаются прямыми и поворачиваются на один и тот же угол.

3.Расстояния между поперечными сечениями не изменяются, т.е. продольные волокна не удлиняются и не укорачиваются.

80